一種變異的改進粒子群優化算法
陳永剛 邱 涌 肖春寶
(河南科技大學電子信息工程學院,河南 洛陽 471003)
1.引言
粒子群優化算法(PSO)是由Kennedy和Eberhart等于1995年發明的一種基于群智能的進化計算技術[1,2],來源于對鳥群捕食的行為研究。后來shi等人[3]引入慣性權重,形成了當前的標準版本。PSO的優勢在于概念簡單,容易實現并且沒有許多參數需要調整,目前已經成功應用于結構設計、神經網絡[4]、多目標優化[5]等工程優化中。
PSO算法收斂速度較快,但會出現早熟收斂,甚至不收斂的情況,尤其對于多峰函數而言不能令人滿意,對高維函數優化在求解質量上和速度上有些缺點。對PSO算法進行改進提高優化性能為該領域的一個研究熱點。相繼出現了一些改進的算法,然而這些算法在一定程度上改善了算法的優化性能,但很難在搜索精度和早熟收斂之間達到平衡。針對上述缺點,本文提出了一種改進的粒子群算法,該算法引入了合作算子[6],在迭代優化過程中對粒子進行兩種合作策略的變異,使粒子群體保持多樣性。本文分析了粒子速度更新公式的基礎上,提出了動態改變粒子的粒子分享個體最優和群體最優的信息比例的方法,使算法初期具有全局搜索能力,后期具有較好的搜索精度。實驗結果表明,該算法具有較好的優化效率。
2.粒子群算法介紹
2.1 PSO算法基本原理
PSO初始化為一群隨機粒子(隨機解),然后通過迭代找到最優解。在每一次迭代中,粒子通過跟蹤兩個“極值”來更新自己。第一個就是粒子本身所找到的最優解,這個叫做個體極值,記為Pi。另一個極值是整個種群目前找到的最優解,這個極值是全局極值,記為Pg。
設搜索空間為D維,總粒子數為n,第i個粒子表示為xi=(xi1,xi2,…xiD);第 i個粒子的歷史最優位置記為 Pi=(pi1,pi2,…piD);整個群體經歷過的最好位置記為 Pg=(pg1,pg2,…pgD),粒子速度記為 Vi=(vi1,vi2,…viD)。則對于每一代,每個粒子的位置根據如下方程變化。
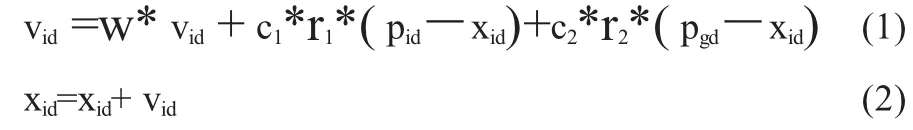
其中c1和c2是非負常數并且通常取值為2,稱為學習因子。r1和r2是介于[0,1]之間的隨機數。每一維粒子的速度都會被限制在一個最大速度Vmax,如果某一維更新后的速度超過用戶設定的Vmax,那么這一維的速度就被設定為Vmax,即 vid∈[-Vmax,Vmax]。
2.2 算法流程
標準PSO的算法流程如下:
Step1:初始化所有粒子,包括隨機位置和速度;
Step2:評價每個粒子的適應值;
Step3:對每個粒子,將其適應值與其經歷過的最好位置Pi作比較,如果較好,則將其作為當前的最好位置Pi;
Step4:對每個粒子,將其Pi與全局所經歷的最好位置pg作比較,如果較好,則重新設置pg;
Step5:根據公式(1)和(2)進行速度和位置(解)的迭代;
Step6:重復Step2~Step5,直到滿足算法停止迭代的條件。
3.改進的粒子群優化算法(IPSO)
標準的PSO算法中,若粒子找到一個最優位置,則其他粒子會迅速向其靠攏,此時若最優位置為局部最優,則粒子就可能陷入早熟收斂。這樣就導致了粒子群體不能在優化空間重新搜索和運動。為了使粒子能進一步進化和繼續優化,本文采用了合作算子對歷史最優粒子進行變異的方法。這樣不僅使變異后歷史最優粒子更好地引導粒子的運動,使粒子擺脫局部收斂。還可以進化整個種群的最優粒子,更好地搜索最優解,提高搜索精度。同時對最優粒子采取保序策略,確保群體最優解向好的方向進化。
3.1 合作算子
設兩個個體粒子為 p1=(x1,x2,…xD)和 p2=(y1,y2,…yD)。如果∈(0,1) 合作策略1中,q和r由式(3)產生: 其中,βk為0和1之間的隨機數。 合作策略2中,由式(4)產生: 其中,1 由于算法的優化效果取決于粒子運動的兩個公式,所以改動公式,就相當于是粒子的運動發生了變化,進而產生不同的優化效果。 從公式(1)可見,粒子速度更新由三部分完成。第一部分反應粒子當前速度的影響,聯系粒子當前的狀態,起到了平衡全局和局部搜索的能力;第二部分反應認知模式的影響,即粒子本身記憶的影響,使粒子具有全局搜索能力,避免陷入局部極小;第三部分反應社會模式的影響,即群體信息的影響,體現粒子間的信息共享。令φ1=c1r1,φ2=c2r2,顯然φ1和φ2是介于0和2之間的隨機數。顯然在算法初期應該增加粒子的群體搜索能力,這樣必須加強粒子本身記憶的影響,削弱群體最優粒子的影響。這時,令φ1=1+φ1/2,φ2=φ2/2,這樣就有,φ1∈(1,2),φ2∈(0,1),較好地增加了個體經驗對粒子速度的影響,提高群體多樣性,從而增加算法的全局搜索能力,有效增強避免早熟收斂能力。算法后期,由于大部分粒子都聚集在最優粒子周圍,為了找到更好的結果,需要增加最優解附近的搜索,需要最優粒子分享更多的信息給整個種群。這時,令 φ1=φ1/2,φ2=1+φ2/2。這樣粒子局部搜索能力得到了加強,提高了優化精度。 本文采用了標準PSO算法和改進算法進行實驗,并將結果進行對比。兩種算法采用相同的參數設置。線性下降的慣性權重的變化范圍是[0.3,0.9]。實驗中的種群規模設置為30,粒子的維數為30,最大的迭代次數為1000次。CS設置為0.5,保證粒子的兩種變異方式都能平均地采用。兩個測試函數如下: Rastrigin函數 Griewank函數 算法迭代次數為1000次。算法對每個函數獨立運行30次,取最優值和平均最優值作對比。結果如表1。 表1 仿真結果 從表中的測試結果中,可以看出本文IPSO算法的最優收斂值和平均收斂值要優于標準PSO,這充分說明了IPSO算法具有更好的搜索精度,較強的抗早熟能力和較快的收斂速度,并且算法也具有較好的穩定性。 本文提出的改進PSO算法,對于每次迭代,粒子群體之間采用合作算子進行變異進化,合作算子通過粒子之間相互作用來增加彼此的適應度,提高了算法的收斂速度和精度。對于算法不同階段粒子運動公式的改變,可以較好地平衡粒子的全局搜索和局部搜索的能力,避免算法陷入早熟收斂。通過對2個基準測試函數的仿真,證明了本文的IPSO算法對于高維、多極值點的函數有較好的效果。 [1]Kennedy J,Eberhart R .Particle swarm optimization[A].Proc IEEE Int Conf on Neural Networks[C].Perth,1995.1942-1948. [2]Eberhart R,Kennedy J.A new optimizer using particle swarm theory[A].Proc 6th Int Symposium on Micro Machine and Human Science[C].Nagoya,1995.39-43. [3]Shi Y,Eberhart R.A modified particle swarm optimizer[C].In:IEEE World Congress on Computational Intelligence,1998:69-73. [4]王建芳,李偉華.基于擴展的T-S模型的PSO神經網絡在故障診斷中的應用[J].計算機科學,2009,36(9):224-245. [5]劉衍民,牛奔,趙慶禎.基于交叉和變異的多目標粒子群算法[J].計算機應用,2011,31(1):82-84. [6]焦李成,劉靜,鐘偉才.協同進化計算與多智能體系統[M].北京:科學出版社,2006.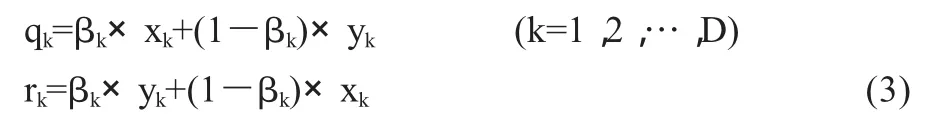
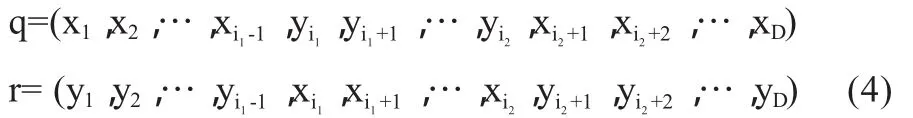
3.2 對運動公式進行動態調整
4.仿真實驗和結果分析
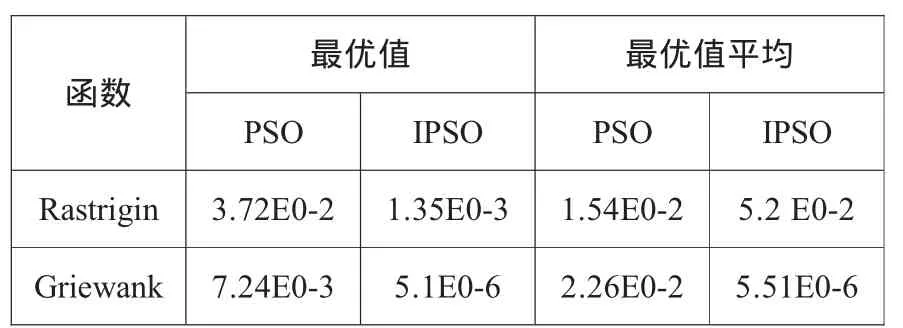
5.結論

