基于徑向基函數神經網絡的網絡流量識別模型

劉 曉

（暨南大學 信息科學與技術學院，廣東 廣州510000）

神經網絡對非線性函數關系具有良好的逼近能力，所以本文提出了一種基于RBF函數神經網絡的網絡流量模型。RBF神經網絡為局部神經網絡模型，計算速度快、實時性好，相對于傳統的線性流量模型具有更高的逼近能力和良好的自適應性，并可克服基于BP神經網絡的流量模型訓練時間長及計算復雜度高的不足。

1 RBF神經網絡結構及學習算法

1.1 RBF神經網絡結構

RBF神經網絡是20世紀80年代由MOODY J和DARKEN C提出的一種神經網絡模型，是具有單隱層的前饋網絡，屬于局部逼近網絡，已證明能以任意精度逼近任一連續函數。RBF神經網絡的結構如圖1所示。

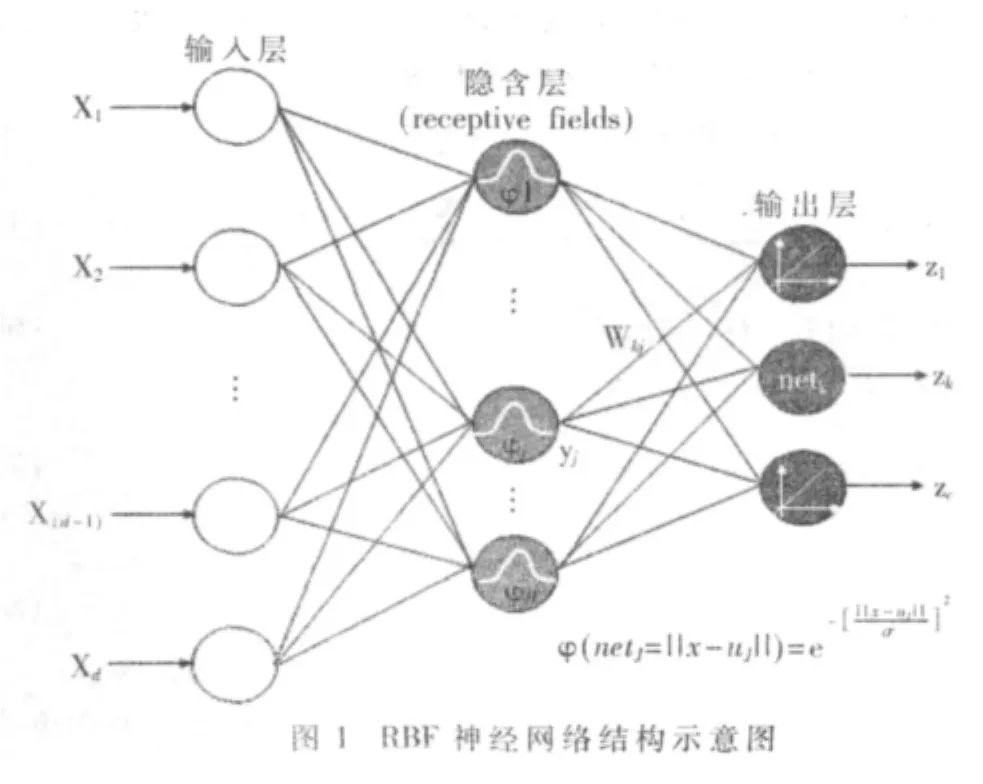
網絡由輸入層、徑向基函數隱含層、輸出層三層構成。低維空間非線性可分的問題總可以映射到一個高維空間，使其在此高維空間中為線性可分[1]。RBF的輸出單元部分構成一個單層感知機，只要合理選擇隱單元數（高維空間的維數）和作用函數，就可以把原來的問題映射為一個線性可分問題[2]。RBF網絡中輸入到隱含層的映射是非線性的，而隱含層到輸出的映射是線性的。隱含層的節點數與實際問題的要求有直接的關聯，過多的節點數會導致學習時間過長和低容錯率，所以必須優化隱含層的節點數。隱含層的節點數可以采用式(1)計算：

其中n是輸入層的節點數，m是輸出層的節點數，a是1～10 的常數[3]。

隱含層基函數采用高斯函數：

隱節點的輸出加權后進入輸出層，輸出層是其隱含層的線性組合[4-5]，即：

其中 x∈Rn為輸入向量，Φ(·)是高斯核函數，‖·‖是歐幾里德范數，ci∈Rn為第 i個隱節點的場中心,σi∈R為第i個隱節點的場域寬度，n是隱含層節點數,wi為第i個隱節點的基函數與輸出節點的連接權值，w0為調整輸出的偏移量。

1.2 RBF神經網絡學習算法

(1)對訓練數據進行聚類，把基函數分別分配給每一個聚類。 選擇一 組初始的中心值{μ?1，μ?2，…，μ?K}，用 K-均值聚類算法計算出中心值μ?k(1≤k≤K)和寬度σ?j:

選入“少兒萬有經典文庫”的原典在人類科學史上的重要性和經典性不容置疑，但其厚重的篇幅和深邃的理論體系，讓一般讀者都可能望而卻步，更不要說理解能力有限的少年兒童。而在這套文庫里，少兒彩繪版呈現出生機勃勃的氣息，吸引著小讀者從容地走進經典。

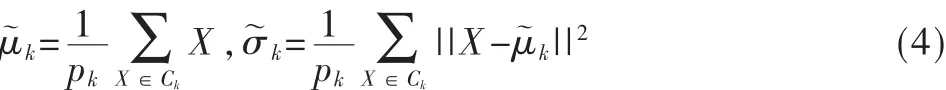
(2)計算隱含層的輸出。

(3)實際輸出與期望輸出進行比較，應用梯度下降法訓練權重，使得均方最小更新權重。

權重的改變值：

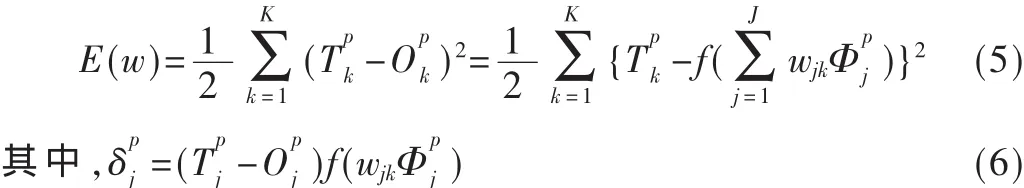
如果是線性的則為：

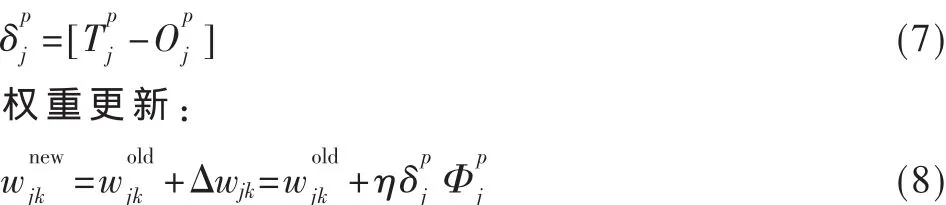
(4)對輸入的N組數據重復步驟(2)～步驟(3)N次。

(5)重復步驟(2)～步驟(4)，直至誤差小到可接受的程度。

2 識別過程

流量識別過程分為四個部分：數據獲取過程、數據預處理過程、數據訓練過程和測試數據分類過程。重點在于建立一個RBF神經網絡模型對網絡流量進行分類。

（1）數據獲取過程是通過數據獲取模塊提取網絡連接記錄和分析特征，以選擇合適的網絡特征屬性作為原始的輸入值。選擇一組最合適的特征子集作為RBF神經網絡的原始輸入值。

（2）數據預處理過程是將特征子集映射到[-1,1]的范圍[4]。

（3）數據訓練過程是將經過預處理后的網絡流量特征子集作為RBF神經網絡模型的訓練集。

（4）根據RBF神經網絡的輸出對網絡流量進行分類。

3 試驗與分析

本文選用流量文庫http://newsfeed.ntcu.net/中給出的兩組實際數據進行實驗，兩組數據分別如表1、表2所示。

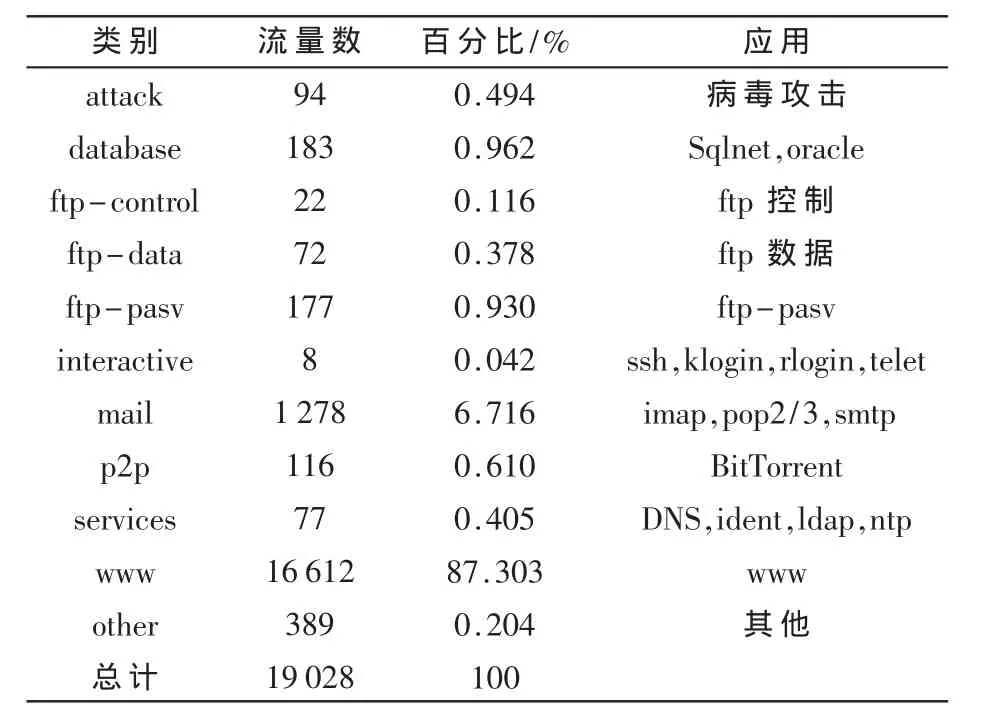
表1 實際數據一

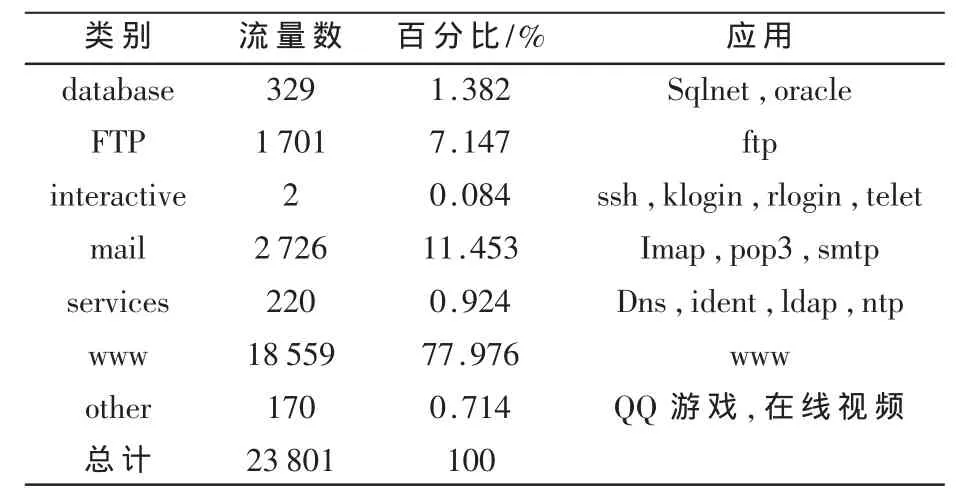
表2 實際數據二

RBF網絡在數據一中采用248個輸入層節點、262個隱含層節點和11個輸出層節點的結構；在數據二中采用248個輸入節點、260個隱含層節點和8個輸出層節點的結構。實驗結果如表3所示。

本文提出了一種基于RBF神經網絡的網絡流量識別方法。通過測試兩組開發的網絡流量數據集，證明該方法具有較高的準確度、低復雜性和良好的自適應性。

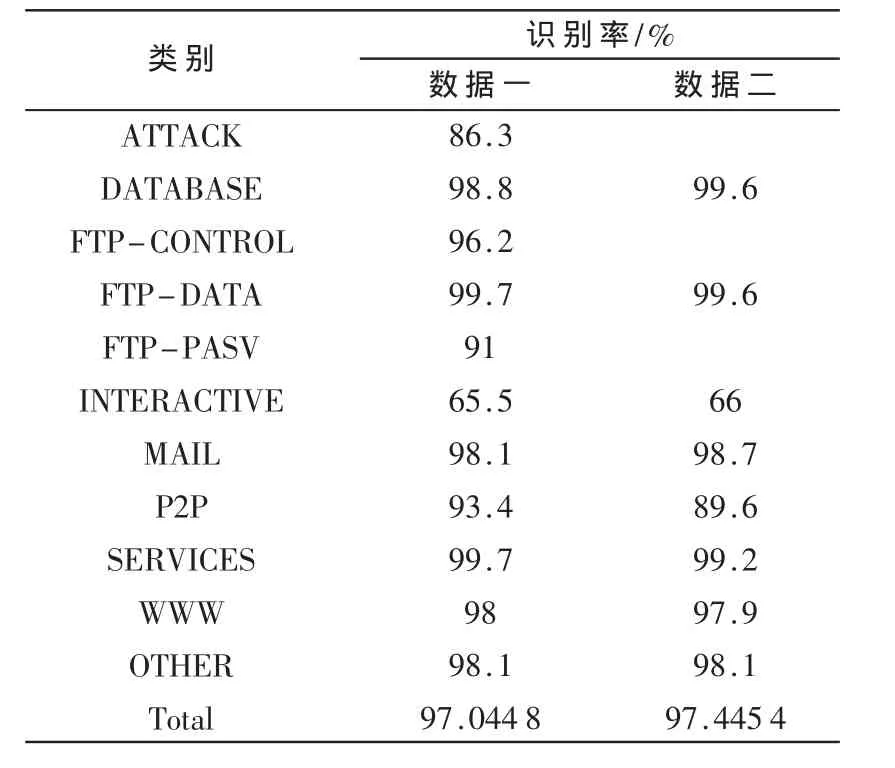
表3 實驗結果

[1]Shi Zhongzhi.Neural Network[M].Beijing：Higher Education Press，2009.

[2]COVER T M.Geometrical and statistical properties of system of linear inequalities with applications in pattern recognition[J].IEEE Transactions on Electronic Computer，1965(14)：326-334.

[3]Fei Sike Technology R&D Center.Matlab Application[M].Beijing：Electronic Industry Press，2005.

[4]MOORE A W，ZUEV D.Discriminators for use in flowbased classification[A].Intel Research，Cambridge，2005.

[5]王俊松.基于Elman神經網絡的網絡流量建模及預測[J].計算機工程，2009(9)：190-191.