基于車頭時距交通信號的模糊控制系統的研究

羅全恒，李佳奇

（河西學院 物理與機電工程學院，甘肅 張掖734000）

隨著我國經濟的持續發展，城市化進程不斷加快，機動車輛快速增加，使得交通出行量不斷增長，城市交通供給嚴重不足。在這種情況下，為了提高城市道路的通行能力，減少交叉路口對車輛的延誤，人們開始研究智能交通系統ITS(Intelligent Transportation System)。模糊控制是一種不需要建立被控對象精確的數學模型的一種智能控制，它是基于一種規則的控制，采用的是語言型控制規則[1-2]，因而控制規則和控制機理容易被人們理解和接納。

自從PAPPIS[3]等人將模糊邏輯[4]應用于城市交叉路口信號控制中以來，國內外許多學者也進行了這方面的研究工作。盡管后續也有很多人研究了雙向車流和多相位的模糊控制系統，但是主要以當前綠燈相位的車輛排隊長度和紅燈相位的車輛排隊長度為模糊控制器[5]的輸入變量，以綠燈相位的綠燈延時為模糊輸出，很少考慮車頭時距[6]這個重要參數。本文將車頭時距作為實現綠燈時間修正的模糊控制器輸入變量之一來提高綠信比，充分利用綠燈時間，從而提高通行能力。

1 系統模型

本文研究的是八車道十字路口，有機動車道和非機動車道，機動車道用到的交通數據來自各個車道的檢測器，每一車道有兩個檢測器，一個設在停車線處，稱為前端檢測器，用于檢測該車道的車輛離開數；另一個設在距停車線一定距離處，稱為后端檢測器，用于檢測車輛到達數，根據檢測算法可以得到某車道上兩檢測器之間的排隊車輛數。所需考慮的車流有東西直行、東西左行、東西右行、南北直行、南北左行和南北右行共6個相位[7-9]，交通信號控制就是決定一個周期內的相位如何變化以及每個相位應該分配多少時間，所以為了控制交叉口的交通信號，首先要選擇組成周期的相位。在自行車和行人流量不大的交叉口，將其合并專用相位，這時采用汽車右行和自行車分時復用一個信號相位的辦法。

2 系統模糊控制算法

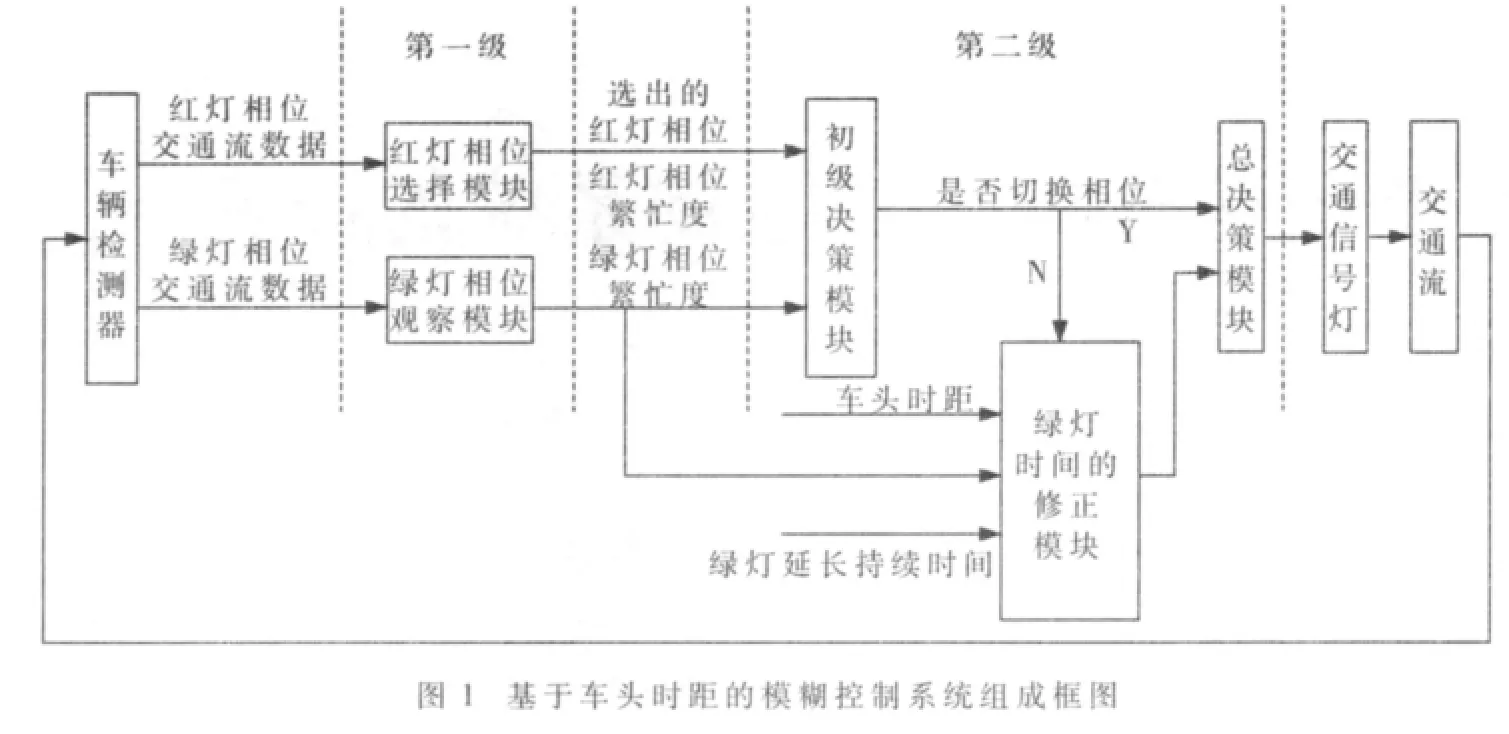
模糊控制模擬了人腦的思維、推理、決策的過程，所以交叉口交通信號的控制就是模仿有經驗的交警指揮過程。根據其指揮過程，設計了系統模糊控制的總體規劃方案，圖1所示即為該方案算法的組成框圖。

第一級為觀測級；第二級為決策級。觀測級包括兩個模塊：紅燈相位選擇模塊和綠燈相位觀察模塊。決策級也包含兩個模塊：初級決策模塊和總決策模塊。每個模塊都是一個子模糊控制器。

算法描述如下：紅燈相位選擇模塊根據車輛檢測器檢測到的交通信息判斷出當前綠燈方向外所有紅燈相位的交通狀況，計算各紅燈相位等待綠燈的緊迫度，并確定出對綠燈要求最為緊迫的紅燈相位作為下一個綠燈相位的候選相位和它的相位緊迫度，將它們傳送給初級決策模塊；綠燈相位觀察模塊根據車輛檢測器檢測到的交通信息判斷出當前綠燈方向交通狀況，確定綠燈相位繁忙度,也將其傳送給初級決策模塊；初級決策模塊紅燈相位等待綠燈的緊迫度和綠燈相位的繁忙度,決定是切換相位還是延長當前綠燈時間。如果是延長該相位綠燈時間，則將該相位綠燈的繁忙度傳送給綠燈時間修正模塊，該模塊根據繁忙度和該相位的車頭時距得出修正時間，從而得到了綠相位總的綠燈時間；如果由紅燈相位選擇模塊選出的相位緊迫度比由綠燈相位觀察模塊觀察的綠燈相位繁忙度高,則初級決策模塊立刻進行綠燈相位的切換，這樣就不需要綠燈時間的修正。

3 模糊控制器的設計

模糊控制器的設計包括兩大部分：第一級的觀測子系統設計和第二級決策子系統的設計。

3.1 綠燈相位觀察模塊

綠燈相位觀察模塊以綠燈相位交通流數據作為輸入，以產生的綠燈相位繁忙度Bt作為輸出。綠燈交通流數據選擇綠燈相位剩余車輛數qg和綠燈相位經過最小綠燈時間后的綠燈延長時間tg。

(1)數據處理與輸入輸出變量的確定

qg=max(qg1，qg2)，式中，qg1和 qg2分別為綠燈相位兩個車流停留在車道上兩檢測器之間的車輛數。

(2)模糊推理關系

3.2 決策級子系統設計

3.2.1 初級決策模塊

初級決策模塊的輸入是候選相位Pr、相位緊迫度Up和繁忙度Bt，輸出是決策程度 Dc。Pr是由紅燈相位選擇模塊選出的相位，Up是此相位的相位緊迫度，Bt是綠燈相位觀測模塊輸出的綠燈相位繁忙度。Dc決定是否將通行權付給候選相位Pr。

(1)模糊推理關系

(2)模糊規則的確定[10-11]與Matlab實現

通過總結實踐和專家經驗，建立了模糊控制規則，原則是：如果候選相位的緊迫度高或當前綠燈相位的繁忙度低，那么這個模塊將停止當前綠燈相位并給候選相位一個綠燈信號。利用Matlab工具箱中Viewsurf菜單命令可以看到模糊控制規則曲面圖。

3.2.2綠燈相位時間修正量模塊

(1)模糊輸入輸出變量

輸入變量：綠燈延長持續時間ET和車頭時距GAP，ET 和 GAP 的模糊語言是：ET={短，中等，長}，GAP={小，中等，大}。

(2)綠燈持續時間ET、車頭時距GAP以及修正時間的賦值表分別如表1～表3所示。

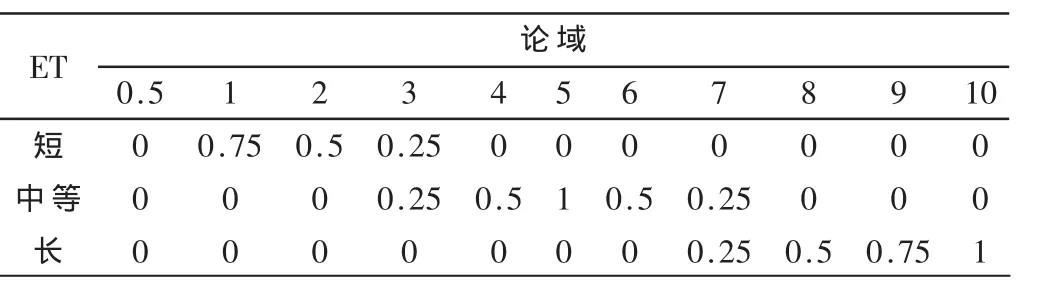
表1 ET的賦值表

(3)模糊規則的確定與Matlab的實現

模糊規則的確定依據:綠燈持續時間長或車頭時距大，則修正時間就長。同樣利用Matlab工具箱中Viewsurf菜單命令可以看到模糊控制規則曲面圖。

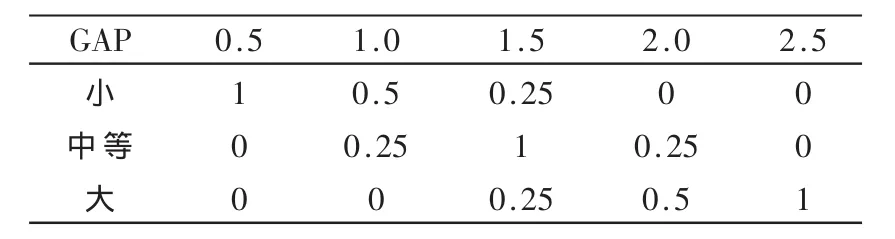
表2 車頭時距的賦值表

表3 修正時間的賦值表

4 仿真結果及其分析

本文以張掖市盤旋路十字路口為研究對象，利用Matlab軟件進行編程仿真，實際測量各個交叉口的交通數據，對一段時間數據進行統計分析，根據分析結果生成車輛數。對于六相位（i=6），每個相位有兩股車流（j=2）的典型交叉口，T時間內交叉口的每輛車的平均延誤時間可用下式表示[12]：

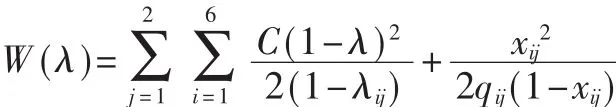
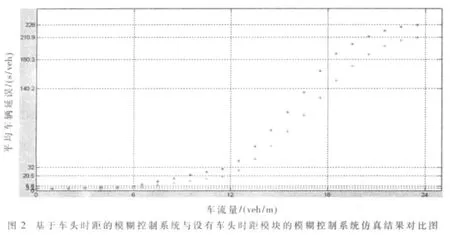
式中，λ為綠信比，C為信號周期，x為相位飽和度，q為車輛到達量，y為流量比率(q/s)。仿真中采用的飽和流量 Sij全部取 2 000 veh·h-1。仿真時間按1 h計算，程序自動計算各方向的車輛到達率和平均延誤時間，從而考察采用不同控制策略時的交叉口的總體運行效率，仿真結果如圖2所示。

圖中的*曲線表示模糊控制系統的控制方案仿真圖，+曲線表示基于車頭時距的模糊控制系統的控制方案仿真圖。經仿真結果數據分析，在交通流低峰期，即0＜λ＜0.1時，基于車頭時距模糊控制系統相比沒有基于車頭時距的模糊控制系統平均車輛延誤減少了43.561%；在交通流中峰期，即 0.1＜λ＜0.3時，前者比后者減少了 32.658%，在交通流高峰期，即 0.3＜λ＜0.4時，前者比后者減少了11.125%。這說明了在交通流不是高峰的前提下，前者比后者控制效果要好得多，大大減少了平均車輛的延誤時間，提高了交叉口的通行能力。

利用自動化手段和技術，實現車輛智能、道路智能必將形成新的智能交通控制系統。模糊控制是一種智能控制,由于其內部并不含有最優控制算法，所以不能針對某一性能指標給出最優解。因此需要改進模糊控制算法,提高模糊控制的精度。本文在自適應模糊控制的基礎上增加了綠燈時間修正模糊算法,即基于車頭時距對綠燈時間進行了微調，對模糊控制精度方面作了有益的嘗試。仿真結果表明,該算法易實現且效果好。

[1]汪培莊.模糊集合論及其應用[M].上海：上海科技出版社，1983.

[2]馮冬青，謝宋和.模糊智能控制[M].北京：化學工業出版社，1998.

[3]PAPPIS C P，MAMDANI E H.A fuzzy logic controler for a traffic junction[J].IEEE Trans on SMC，1997，7(10)：707-717.

[4]褚靜.模糊控制原理及應用[M].北京：機械工業出版社，2005.

[5]華寶玉，何迪.交叉口信號協調控制適用性仿真研究[J].鐵路計算機應用，2007，16(7)：12-15.

[6]陳光勤.基于車頭時距的快速公交車輛交叉口信號優先[J].交通與計算機，2005，23(3)：11-15.

[7]LEE J H，KWANG H L.Distributed and cooperative fuzzy controllers for traffic intersections Group[J].IEEE Transactions on System，Man and Cybernetics，1999(29)：263-271.

[8]陸化普，李瑞敏.智能交通系統概論[M].北京：中國鐵道出版社，2004.

[9]交通部公路科學研究所.中國智能交通系統體系框架研究總報告[R].北京：交通部公路科學研究院，2001.

[10]CHIU S.Adaptive traffic signal control using Fuzzy logic[C].Proceedings of the IEEE Ingelligent Vehicles Symposium.1992：98-107.

[11]OSTERGARAD J J.Fuzzy logic control of a heat exchange process[J].in Fuzzy AUtomata and Decision Processes.Amsterdam：Gupta MM.Et.Eds.NorthHolland，1997(3)：48-65.

[12]王長軍，盧靜.基于思維過程的單交叉路口多相位模糊控制算法研究[J].城市交通，2004，2(3)：14-16.