多饋入電壓源直流對配電網穩定性的影響分析

阮思燁，李國杰

(1.國家電網公司運行分公司，北京市，100052;2.電力傳輸與功率變換控制教育部重點實驗室(上海交通大學)，上海市，200240)

0 引言

近年來，受端系統的輸電問題引起了電力工作者的廣泛關注。傳統的交流輸電技術在受端系統中的應用存在著走廊不足、供電電壓不穩等問題［1-2］。然而直流輸電恰好能解決這些問題，其不僅比交流輸電占有空間小，而且能輸送更多的功率［3］。目前存在的直流輸電方式有2種:電流源換流器型直源輸電技術(current source coverter high voltage direct current，CSC-HVDC)和電壓源換流器型直流輸電技術(voltage source coverter high voltage direct current，VSC-HVDC)。CSC-HVDC 技術在受端系統中的應用存在著局限性:由于許多受端系統是無源網絡，而晶閘管的CSC-HVDC無法向無源網絡供電［4］;即便在有源網絡中，近距離多饋入CSC-HVDC之間的控制還會相互影響導致換相失敗［5］。相比于CSCHVDC技術，VSC-HVDC在城網中應用擁有極大的優勢:無換相失敗、可提供交流電壓支持、改善電能質量，適合于向弱系統甚至無源網絡供電、故障后快速恢復，可以形成靈活的直流和交流互聯網絡等［6］。

鑒于VSC-HVDC的諸多優點，國內外學者在VSCHVDC的運行和控制等方面進行了深入的研究。文獻［7］設計了VSC-HVDC的穩態逆模型控制器;文獻［8］提出了三相電壓不對稱時VSC-HVDC的控制策略;文獻［9］實現了VSC-HVDC本身控制與發電機勵磁控制的優化結合;文獻［10］建立了VSC-HVDC的小信號動態模型，并利用極點配置技術設計了VSC-HVDC的附加阻尼控制器。雖然文獻［7-10］均涉及VSC-HVDC的數學模型及控制原理，但只能在有源系統中工作;文獻［2，11］針對無源系統供電進行了研究并設計了定交流電壓控制，但是只考慮了單饋入VSC直流的供電，從結構上考慮，單饋入的輸電方式不能保證城網用電可靠性，而且隨著受端用電量的不斷提升，增加輸電線路是不可避免的。文獻［2，11］針對單饋入設計的控制方法難以方便地推廣到多饋入VSC直流的系統中。

本文將設計一種多饋入電壓源直流模式下基于有功功率和交流電壓調節的電壓源換流站控制器，采用特征值方法分析控制設計對于系統穩定的影響，并在此基礎上進行仿真驗證。

1 系統模型介紹

一個簡化的多饋入電壓源直流對無源配電系統供電模型如圖1所示。配電網絡包括3個負荷P1L、P2L和P3L(假設有P1L=P2L=P3L=PL/3，PL為總負荷量)，由3條VSC-HVDC線路實現外部的供電，VSC換流站的等效阻抗為xf。

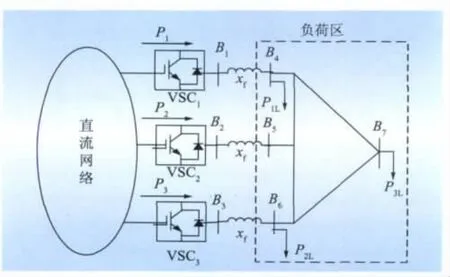
圖1 多饋入VSC直流系統模型Fig.1 System model of multi-infeed VSC-HVDC

由于VSC-HVDC直流側控制已經在文獻［11-12］中詳細介紹過，本文就不再進行討論，將直流網絡簡化為一直流源，重點設計VSC-HVDC連接無源配電網的逆變站的控制策略。

VSC-HVDC逆變站的控制設計如圖2所示，主要包含有功功率控制環和交流電壓控制環2部分，分別類似發電機控制中的功率調速環節和電壓控制環節。

圖2中i=1，2，3。功率控制的工作原理如下:一旦檢測到功率設定值Pio和測量值Pei的偏差，則這個偏差經過PI環節(k1+k2/s)調節VSC逆變站側電壓ui的頻率ωi，而頻率的調節量Δωi經過反饋環節kf得到ΔPio，影響上述PI環節的輸入，從而形成閉環控制系統。隨著頻率的改變，系統會自動調整有功輸出并使系統潮流最終平衡，穩態VSC輸出有功輸出為ΔPio-kfΔω，Δω為穩態頻率偏差。kf值的大小決定了各VSC站發電量變化的分配。本文設定各個VSC站采用相同kf，即平均發電量的變化。

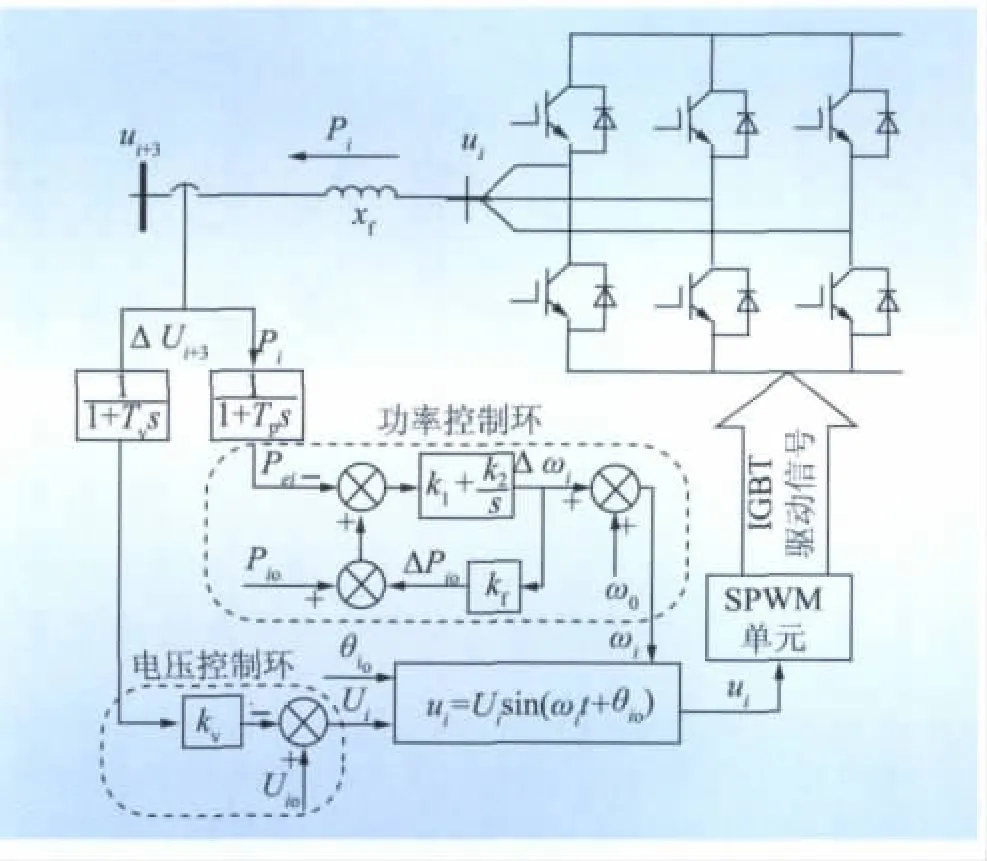
圖2 VSC逆變站側的控制設計Fig.2 Control design for inverter of VSC

根據上述分析得到系統穩態時的有功功率平衡方程為

一旦交流電壓控制環檢測到交流母線電壓Ui+3變化，將通過線性比例kv相應地改變VSC輸出電壓Ui，從而確保配電網電壓維持在指定的水平。

為了盡量減小測量值干擾，在功率和交流電壓測量中加了一階低通濾波，時間常數分別為Tp和Tv。

2 VSC-HVDC控制的特征值分析

在控制當中經常碰到這樣一種情況:當系統進入某個狀態后，開始時能夠勉強正常工作，之后系統就逐漸失穩，這屬于小擾動穩定問題。在本文中，為保證所設計控制器的可靠性，特別采用小信號模型利用特征值分析控制器在不同的運行點或是采用不同控制系數對于系統穩定的影響。

由于所研究系統中不含無窮大母線，需要選擇1個VSC站(VSC3)輸出的角度作為參考(因此有Δθ3=0，sΔθ3=0)［13］。系統的小擾動模型可表示為

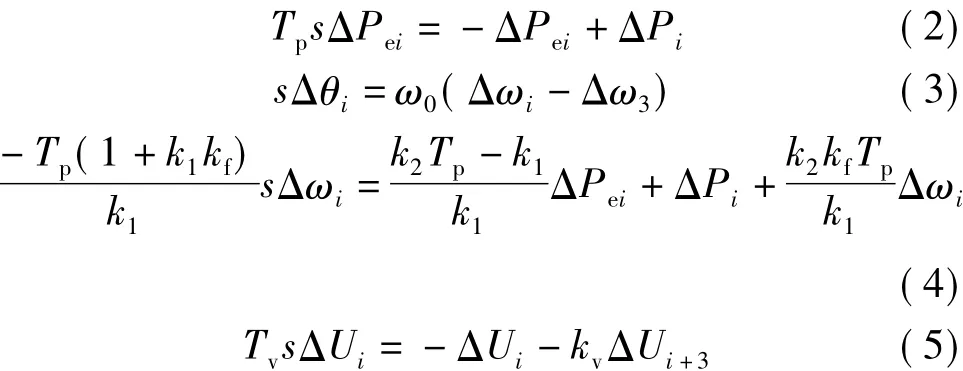
考慮到各個節點的功率平衡，有

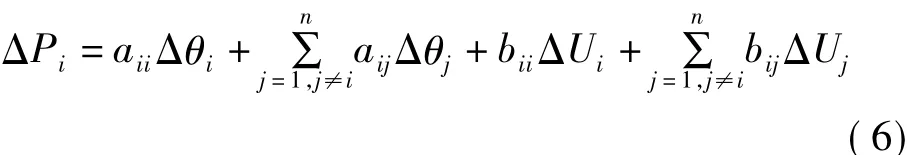
式中:i=1…7;ΔPi、ΔQi為各個節點的注入功率，并有 ΔPi=ΔQi=0，i=4…7，恒功率模型;Ui，θi為各個節點上的電壓幅值和相位;aii、aij、bii、bij、cii、cij、dii、dij參見附錄。

系統狀態方程為

式中:A11，A12、A21、A22參見附錄;M1、M2、X1、X2為

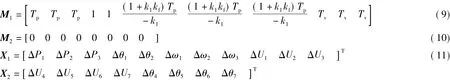
消去數組變量X2可得

控制器的控制系數以及運行點對于系統穩定的影響可以通過這3組的特征值的大小反映出來。其中λ1～λ5相對其他特征值離虛軸最近，因此對于系統的穩定影響也最大。

受篇幅限制，本文中只考慮交流電壓控制系數kv、功率控制系數kf、總體負荷量PL和VSC1輸出功率P1占整體供電的大小不同時系統特征值的變化。其余系統參數如下:Tv=Tp=0.04，k1=0.01，k2=0.2，xf=0.41，x45=j3.1，x47=4.1，x56=3.59，x67=3.1(所有參數都用標么值表示，近似忽略線路中電阻的影響)。

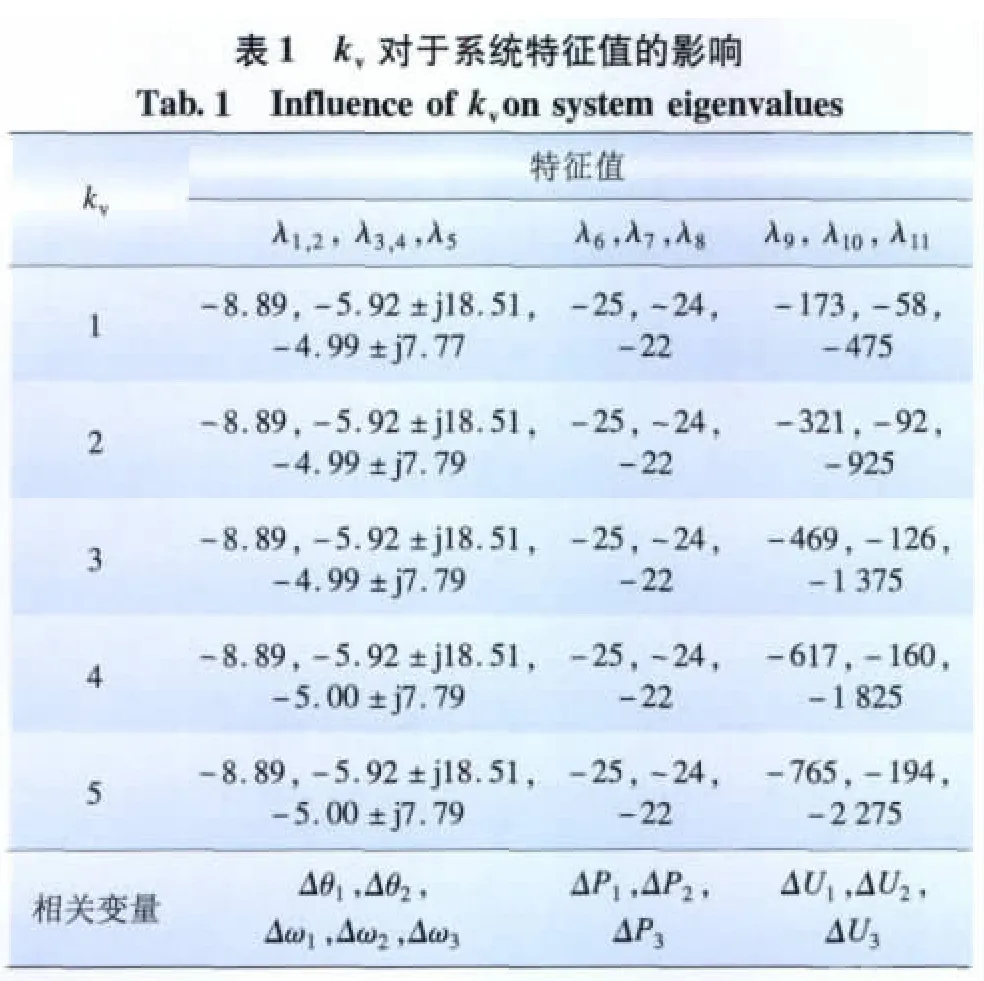
改變 kv(kf=80，PL=1.8，P1=P2=P3=0.6)對于狀態矩陣特征值的影響見表1。kv為交流電壓控制系數，kv越大對于電壓的控制效果越好，由表1可見，kv只影響電壓模式特征值λ9～λ11。隨著kv的增大，對應的電壓模式的阻尼隨之增大。但由于此時λ9～λ11相對其他特征值而言遠離虛軸，因此kv的增大對于系統整體穩定的影響并不大。

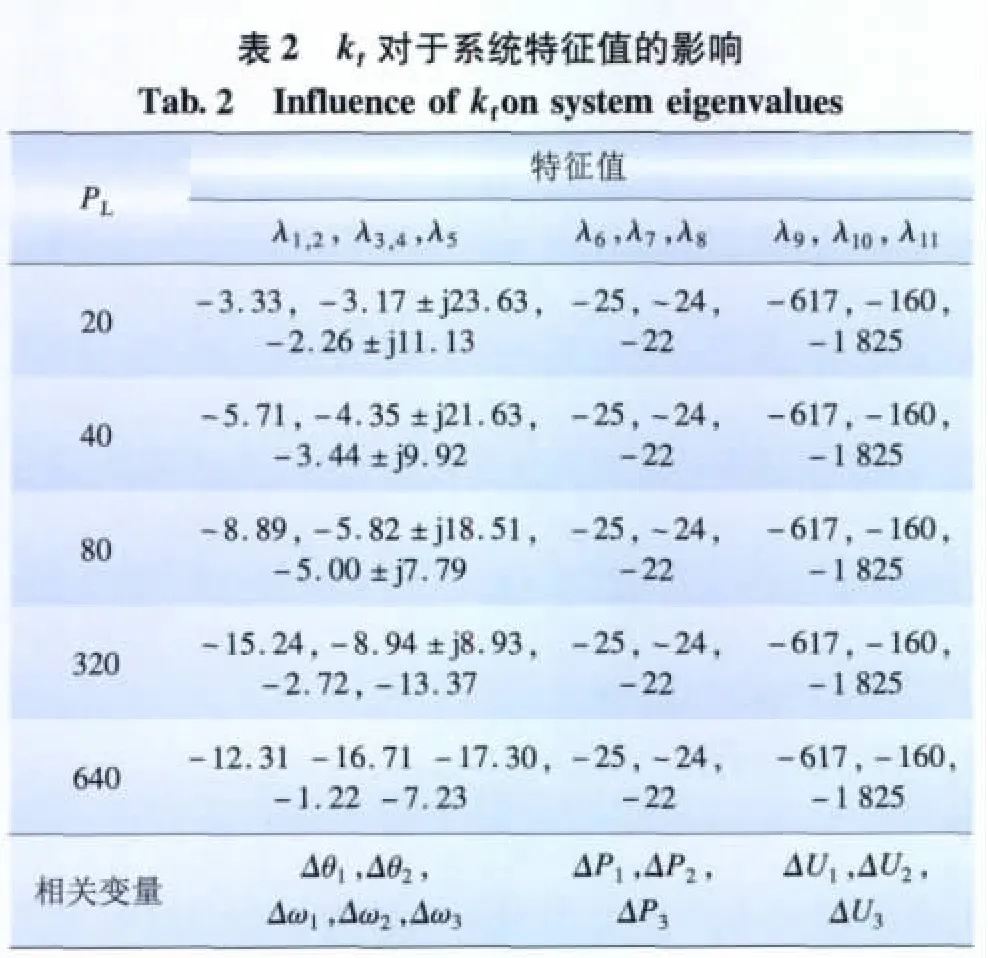
改變 kf(kv=4，PL=1.8，P1=P2=P3=0.6)對于狀態矩陣特征值的影響見表2。kf為功率控制系數:kf的變化只影響角度頻率模式λ1～λ5。由于角度頻率模式下的特征值離虛軸最近，因此這組特征值的改變對于系統的穩定影響最大。起初隨著kf越大角度頻率模式的阻尼隨之增大，系統穩定性也跟著提高。當kf增大到一定程度后，kf值繼續增大則會削弱角度頻率模式的阻尼，即減小系統穩定性。

?

?

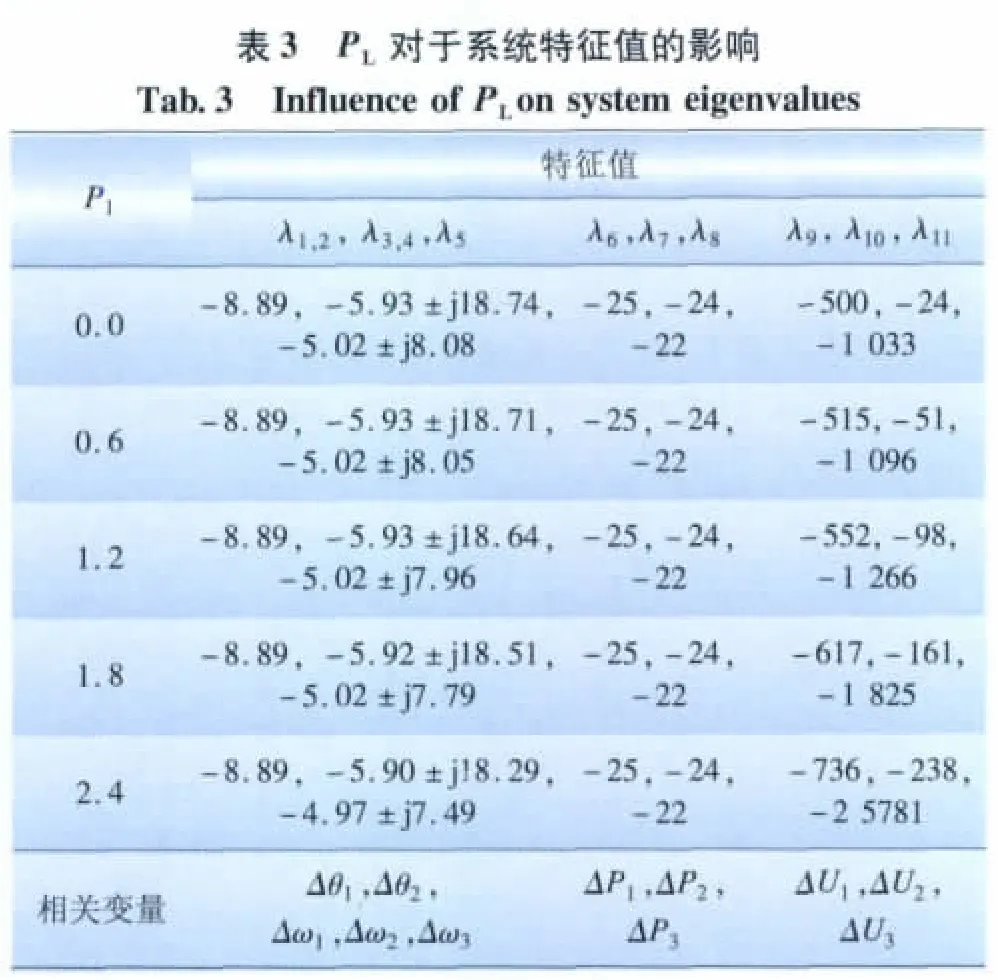
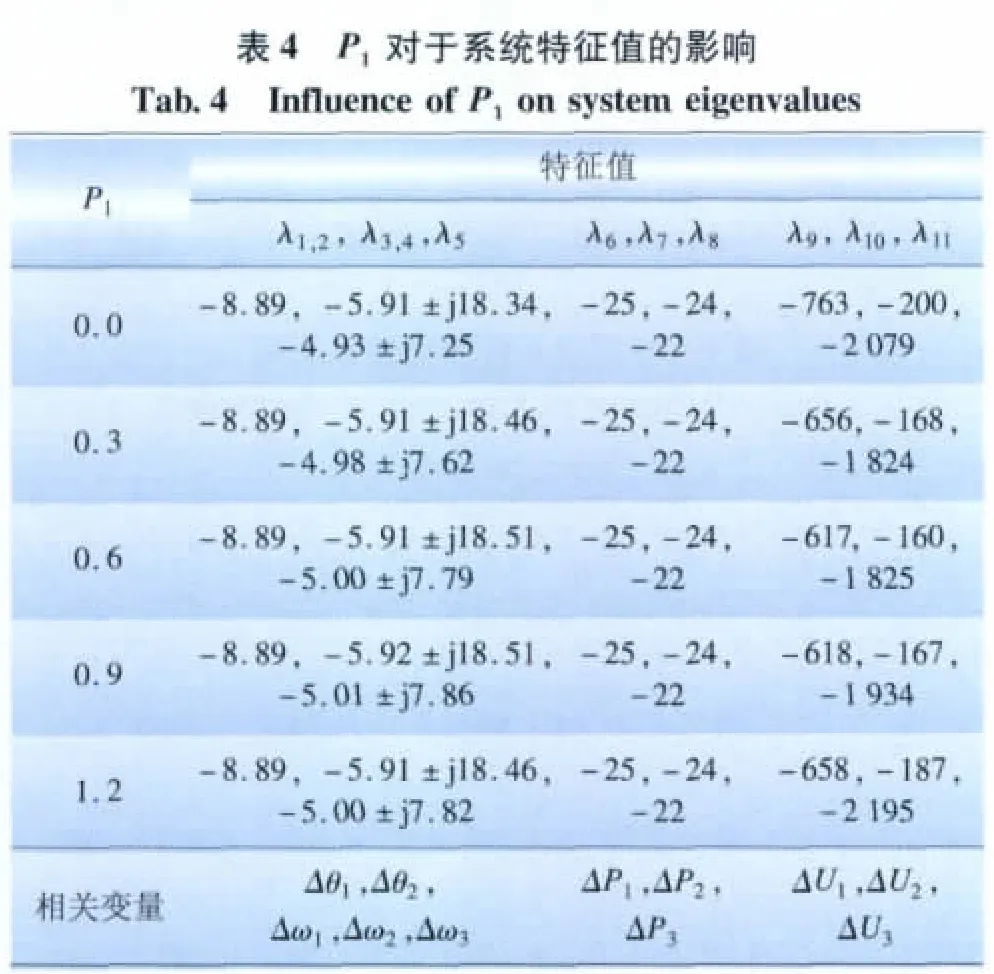
改變PL(kv=4，kf=80，P1=P2=P3=PL/3)對于狀態矩陣特征值的影響見表3。改變P1占整體供電的大小(kv=4，kf=80，PL=1.8，P2=P3=(PL-P1)/2)對狀態矩陣特征值的影響見表4。

表3～4體現了不同運行點下系統的控制效果。系統負荷PL的變化或是P1占整體供電大小的變化對于系統穩定性的影響不大。這意味著設計者將不必根據不同的運行點調整參數:在kv=4、kf=80這組控制系統下，系統在不同運行點都有著很好的控制效果。

?

?

3 仿真驗證

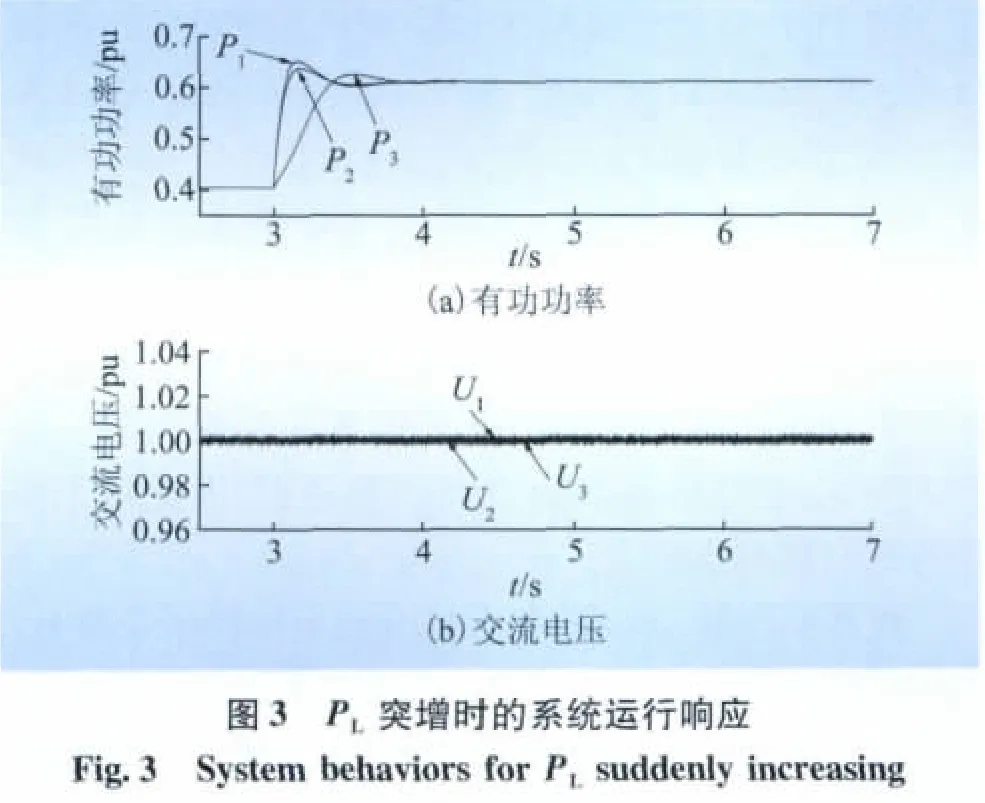
為驗證所建控制器模型以及特征值分析結果的正確性，本文用工業仿真軟件EMTDC-PSCAD對圖1所示的系統進行了數字時域仿真研究。由于篇幅限制，仿真著重討論了系統在負荷突變、調節VSC1輸出功率這2種情況下系統的響應，如圖3～4所示。圖中給出3條VSC-HVDC輸出的有功功率P1、P2和P3以及受控的端電壓U1、U2和U3。

系統的額定容量為100 MVA，額定電壓為35 kV。VSC-HVDC的逆變站采用相同設計:kf=80，kv=4，Tv=Tp=0.04，k1=0.01，k2=0.2，xf=0.41。線路阻抗x45=j3.1Ω，x47=j4.1Ω，x56=j3.59Ω，x67=j3.1Ω。

3.1 負荷突增

系統在負荷突增過程中的響應曲線如圖3所示。初始狀態時系統P1=P2=P3=PL/3=0.4 pu，3 s時負載PL由1.2 pu突增至1.8 pu。各個VSC-HVDC的功率控制環節檢測到外部功率的變化，將通過功率控制環節迅速改變各自有功輸出，并使得最終的系統功率平衡。系統中變化的這部分負荷由3條VSCHVDC均攤(各0.2 pu)。與此同時，電壓控制環節也確保了各自交流電壓的穩定。

3.2 調節VSC-HVDC的輸出功率

采用功率控制環節后，也為系統管理人員調節VSC-HVDC供電量提供了便利，而不是僅僅根據外界的功率變化被動地改變輸出。舉一個簡單的例子:系統管理人員可以通過調整功率設定值P1o的大小，改變P1占整體供電的大小(從0.6 pu增加到0.9 pu)。

調節VSC-HVDC的輸出功率時的運行響應如圖4所示。隨著P1上升0.3 pu，P2和P3相應各下降了0.15 pu。在此過程中，VSC-HVDC控制的端電壓U1、U2和U3幾乎沒有變化。

通過以上結果看到，在給定的控制設計下，系統在不同的運行點都能保持很好的穩定性。盡管控制分析設計是針對低頻小信號模型的，但這樣設計出的閉環控制系統在大擾動下仍然具有比較好的動態性能。使得系統在受到較大負載擾動或有功指令作較大階躍時能快速準確地進入期望的穩態運行點。

4 結語

本文研究結果表明:多饋入VSC-HVDC能穩定、靈活、高效地向城網輸電，而且各條VSC-HVDC不需要協調控制并基于本地信號，系統運行有良好的穩定性。VSC-HVDC的控制模塊在引入了功率控制環節和交流電壓控制環節后，VSC-HVDC也能自動根據外界的變化調整功率輸出，或者是通過人為改變其功率設定值的手段調整VSC-HVDC供電量輸出，同時控制模塊中的電壓環節能很好地維持系統內的電壓水平。

［1］Zhang Justinjin，Liu Qianjin，Christian E，et al.Investigation for new solutions for mega city power grid issues［C］//2nd CICED Conference.Beijing，China，2006:17-20.

［2］梁海峰，李庚銀，李廣凱，等.向無源網絡供電的VSC-HVDC系統仿真研究［J］.電網技術，2005，29(6):45-50.

［3］徐政.交直流電力系統動態行為分析［M］.北京:機械工業出版社，2004.

［4］Kundur P.Power System Stability and Control［M］.Montreal:McGraw-Hill，1994.

［5］項玲，鄭建勇，胡敏強.多端和多饋入直流輸電系統中換相失敗的研究［J］.電力系統自動化，2005，29(11):29-33.

［6］文俊，張一工，韓民曉，等.輕型直流輸電:一種新一代的HVDC技術［J］.電網技術，2003，27(1):47-51.

［7］張桂斌，徐政，王廣柱.基于VSC的直流輸電系統的穩態建模及其非線性控制［J］.中國電機工程學報，2002，22(1):17-22.

［8］李金豐，李廣凱，趙成勇，等.三相電壓不對稱時帶有電壓源換流器的HVDC系統的控制策略［J］.電網技術，2005，29(16):16-20.

［9］胡兆慶，毛承雄，陸繼明.一種優化控制策略在基于電壓源換流器的 HVDC 系統中的應用［J］.電網技術，2004，28(10):38-41.

［10］鄭超，周孝信.基于電壓源換流器的高壓直流輸電小信號動態建模及其阻尼控制器設計［J］.中國電機工程學報，2006，26(2):7-12.

［11］陳海榮，徐政.適用于電壓源型高壓直流輸電的控制策略［J］.電力系統自動化，2006，30(19):28-33.

［12］Lu Weixing，Ooi B T.DC overvoltage control during loss of converter in multiterminal voltage-source converter-based HVDC［J］.IEEE Trans on Power Delivery，2003，18(3):915-920.

［13］倪以信，陳壽孫，張寶霖.動態電力系統的理論和分析［M］.北京:清華大學出版社，2002.