可再生能源發電優化模型及其應用

從榮剛

(1.華北電力大學經濟與管理學院，北京市 102206;2.瑞典隆德大學環境與氣候研究中心，瑞典隆德市 22362)

0 引言

我國政府承諾到2020年中國可再生能源消費要占一次能源消費的15%，使可再生能源的發展在我國受到了空前的關注。一方面，開發可再生能源對于保障能源的供給安全意義重大［1］;另一方面，20世紀80年代以后，隨著全球氣候變暖和大氣環境質量的急劇下降，人們對環境保護和可持續發展問題達成共識。

可再生能源發電是可再生能源的主要利用領域之一。影響可再生能源發電的主要因素有:技術開發利用成本、資源潛力、技術成熟度、經濟發展和環境約束等［2-3］。對可再生能源發電的最大利用規模和結構進行科學的分析，有助于國家相關部門和電網公司提早開展規劃，減少過剩投資和不足投資的可能性，為可再生能源的發展提供輸送保障，因此具有深刻的現實背景和很高的應用價值。

20世紀80年代，國外對可再生能源的綜合利用進行了研究。文獻［4］指出，從能源生產和利用的角度來看，基于太陽能、風能和生物質能的可再生能源集成利用系統(integrated renewable energy system，IRES)的概念是可行的。文獻［5］利用線性規劃方法開發了IRES模型，其目標是在能源和電力的資源約束下，最小化每年的成本。文獻［6］立足于技術經濟的觀點設計IRES模型，并且把電力供給的損失作為重要的系統變量。文獻［7］開發了最優可再生能源模型(optimization renewable energy model，OREM)，在社會接受度、資源、需求和可靠性條件等約束下最小化成本與效率的比值，共考慮了約38種不同的可再生能源選項。文獻［8］利用修正的計量數學模型，基于能源-環境-經濟的數學規劃模型和OREM模型研究了印度可再生能源的最優利用問題，充分考慮了成本、效率、社會接受度、可靠性、潛力和環境等因素的影響。

本文采用數學優化思想對可再生能源發電進行綜合規劃，所提出的模型充分考慮了可再生能源技術的學習效應及其技術成熟度等因素對可再生能源發電規?；l展的影響，并將模型實現動態化，以實現對可再生能源發電在一段時期內的發展路徑進行優化。

1 可再生能源發電成本變化規律

1.1 考慮最低單位投資成本的學習曲線模型

可再生能源的發電成本是影響可再生能源發電規?；l展的重要因素之一。從國內外的經驗來看，學習曲線模型被廣泛用來描述和預測可再生能源發電成本下降的規律，其核心思想是當可再生能源發電的累積裝機容量每增加1倍，其單位建設成本就出現一定比例的下降［1-15］。本文考慮了最低單位投資成本(即風電機組投資成本的下降必然存在一個下限)，嘗試通過分析中國主要的3種可再生能源發電(風電、太陽能光伏發電和生物質發電)的累積裝機容量與單位投資成本的關系，來揭示其投資成本的變化趨勢。

可再生能源的單位投資成本與累積裝機容量之間的關系為

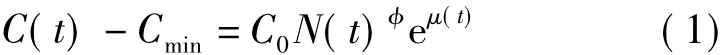
式中:C(t)為單位機組投資成本;Cmin為單位機組投資成本下限;C0為初始時刻的單位機組投資成本;N(t)為機組的累積裝機容量;φ為累積產量對單位投資成本的彈性系數;μ(t)為隨機干擾因素。

為了方便計算，對(1)式進行變換，得到

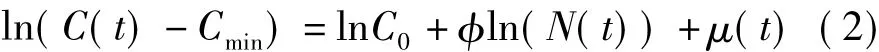
這樣，利用最小二乘法就可以估算出累積裝機容量對單位投資成本的彈性系數。

1.2 3種可再生能源發電的學習曲線效應

根據學習曲線模型，得到我國風電和太陽能光伏發電單位投資成本的學習效應，結果如表1、2所示。

表1 風電的學習曲線效應Tab.1 Learning curve effect of wind power

表2 光伏發電的學習曲線效應Tab.2 Learning curve effect of photovoltaic power generation

目前，各類生物質發電尚未進入規模化發展階段，相關數據缺乏。根據文獻［13］的研究結果，生物質發電的學習曲線設定為

式中:Cb(t)為生物質發電單位機組投資成本;Nb(t)為機組的累積裝機容量。

2 可再生能源發電技術成熟度

2.1 可再生能源技術成熟度模型

可再生能源的規?；l展離不開相關的技術支撐。技術系統的進化要經歷嬰兒期、成長期、成熟期和衰退期4個階段，這些階段組成了其技術生命周期，通常用S曲線表示［14］。一方面，在可再生能源建設初期，受需求、電網建設等約束，可再生能源發展呈現緩慢發展趨勢;另一方面，在可再生能源建設的中后期，隨著相關配套設施和市場的逐漸成熟，可再生能源發展將呈現快速發展直至飽和的特點。實際上，可再生能源發展的規模應該小于或等于S型曲線的預測結果，即S型曲線預測的應為累積裝機容量的上限(潛力)。本文采用S型曲線對可再生能源發電的技術成熟度進行建模，技術擴散模型為

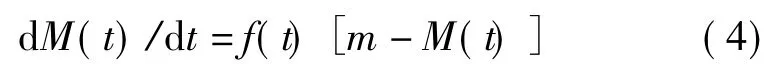
式中:M(t)為t時刻可能的最大裝機容量;m為理論上的最大裝機容量;f(t)為時間依賴函數，其表達式為

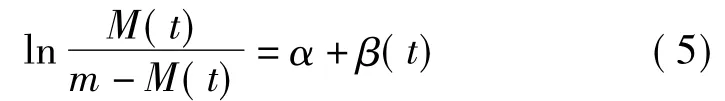
式中:α 和 β 是待估參數［15］。

2.2 3種可再生發電的技術成熟度效應

通過對中國風電累計裝機容量的擬合，得到風電累積裝機容量的S型曲線模型的參數，結果如表3所示。根據模型估算，2015年中國風電累計裝機容量潛力可達到92 GW，2020年可達到233 GW。

表3 風電累積裝機容量的S型曲線模型擬合參數Tab.3 Fitting parameters of S-curve model for wind power’s cumulative installed capacity

采用同樣的方法對光伏發電進行計算，得到光伏發電累積裝機容量的S型曲線模型的參數，結果如表4所示。根據模型估算得出，2015年中國光伏發電累計裝機容量潛力可達到800 MW，2020年可達到2 668 MW。這里預測的結果和07年發布的《可再生能源中長期發展規劃》類似，由于最新的《新能源發展規劃》草案將原來的規劃值提高了10多倍，在后面的模型分析中，將對應的預測值擴大10倍處理。

表4 光伏發電累積裝機容量的S型曲線模型擬合參數Tab.4 Fitting parameters of S-curve model for photovoltaic power’s cumulative installed capacity

由于我國生物質發電起步較晚，尚缺乏一定量的歷史數據，生物質發電的技術成熟度效應主要是根據相關的生物質發電廠建設規劃來進行判斷。2010年生物質發電裝機容量潛力可達到5 500 MW，2020年可達到30 000 MW。

3 中國可再生能源發電優化模型

根據技術擴散和經濟約束等條件，預測2015、2020年我國可再生能源發電(風電、光伏發電和生物質發電)的總體利用規模及結構。借鑒 IRES和OREM可再生能源綜合利用模型的思想，選用運籌學中的動態優化模型來計算。目標函數是最大化3種可再生發電的總發電量，風電、光伏發電和生物質發電的年平均可利用時間分別為2 000、1 300、2 380 h，約束條件包括:(1)各種可再生能源發電的裝機容量小于其各個時間點的最大容量值(由技術成熟度模型給出);(2)各種可再生能源發電裝機的投資在經濟可承受的范圍內;(3)可再生能源發電的上網規模小于一定的比例(并網限制);(4)各種可再生能源發電滿足國家規劃。控制變量為2011—2020年3種可再生能源發電的新增裝機容量，一方面其需要在各個時間點滿足各方面的約束;另一方面，各個時間點的裝機容量會對以后的單位成本產生影響(學習效應)。具體的優化模型為

式中:Nw為風電的裝機容量;Ns為光伏發電的裝機容量;Nb為生物質發電的裝機容量。模型的約束條件為

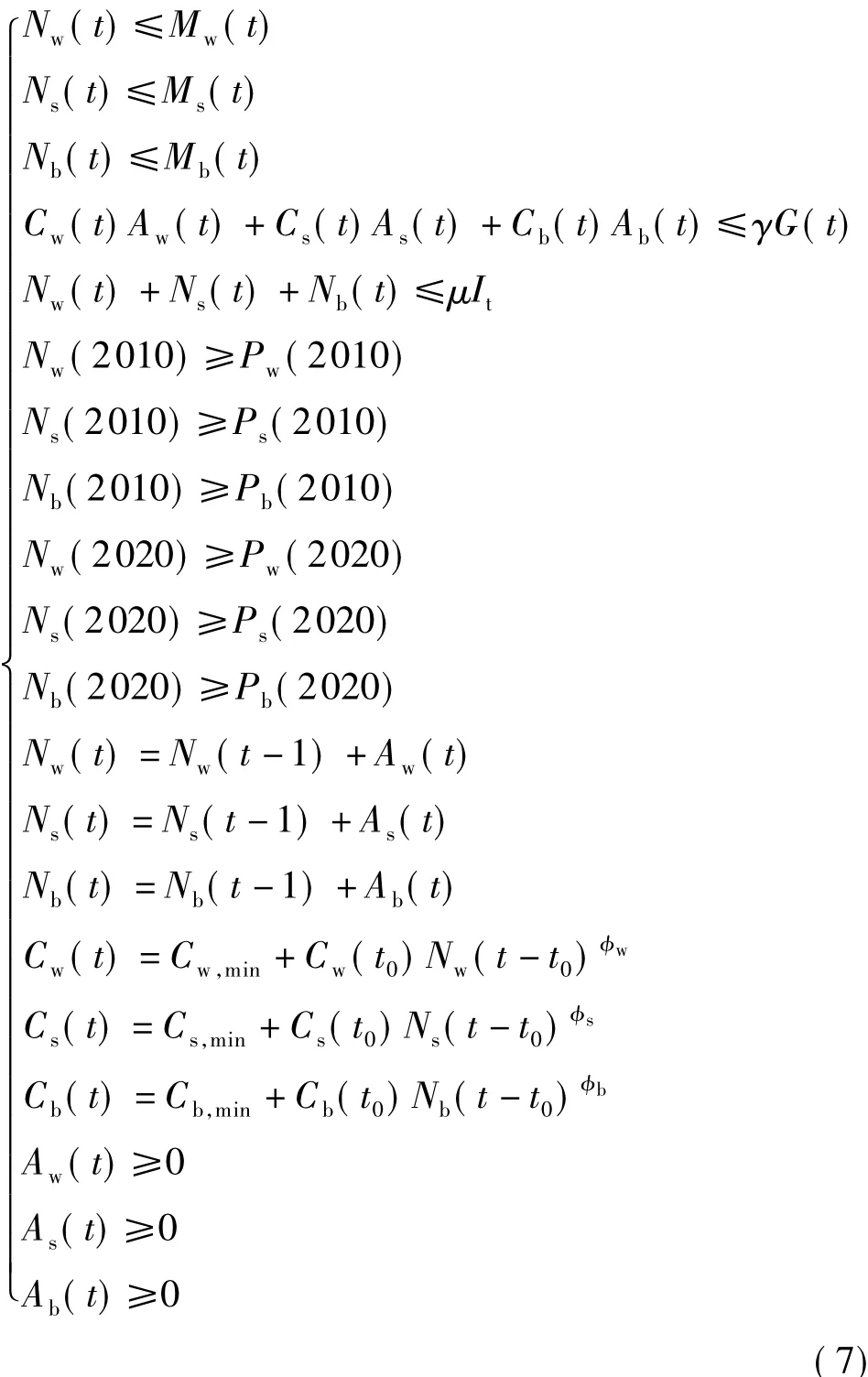
式中:Mw為風電的最大裝機容量;Ms為光伏發電的最大裝機容量;Mb為生物質發電的最大裝機容量;Cw為風電的單位裝機成本;Cs為光伏發電的單位裝機成本;Cb為生物質發電的單位裝機成本;Aw為風電的年新增裝機容量;As為光伏發電的年新增裝機容量;Ab為生物質發電的年新增裝機容量;γ為GDP中用于可再生發電方面的投資比例;G(t)為第t年的GDP總量;μ為可再生能源發電最大上網比例;It為t時刻的總裝機量;Pw為風電的裝機規劃量;Ps為光伏發電的裝機規劃量;Pb為生物質發電的裝機規劃量;Cw，min為風電的最小裝機價格;Cs，min為光伏發電的最小裝機價格;Cb，min為生物質發電的最小裝機價格。

4 模型計算結果和敏感性分析

4.1 模型計算結果

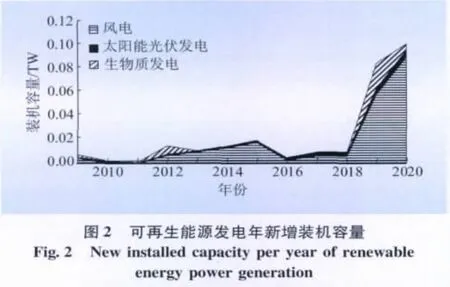
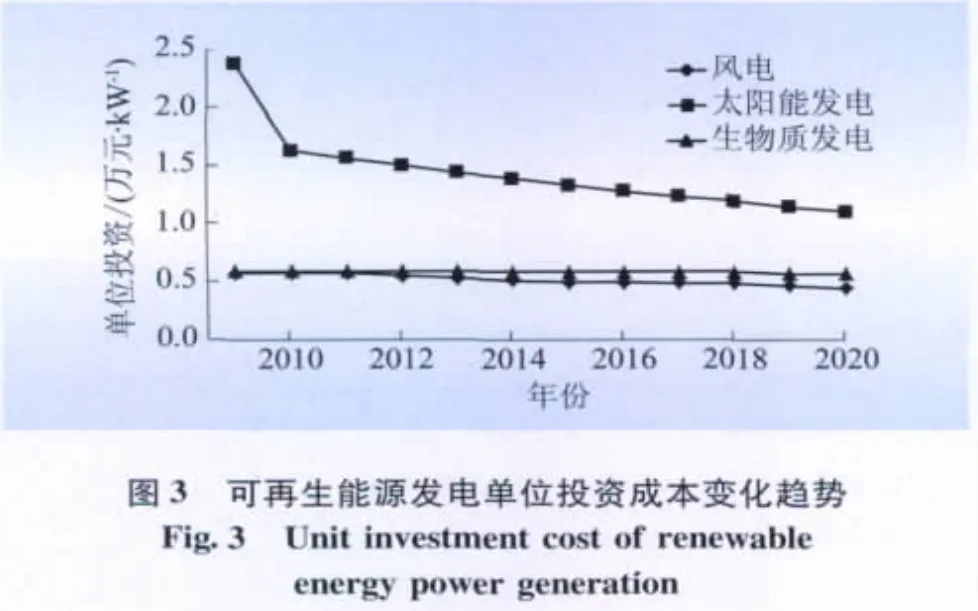
利用本文提出的模型，分別計算了3中可再生能源發電在最大利用情景下的累計裝機容量、年新增裝機容量、單位投資成本，結果如圖1—3所示。

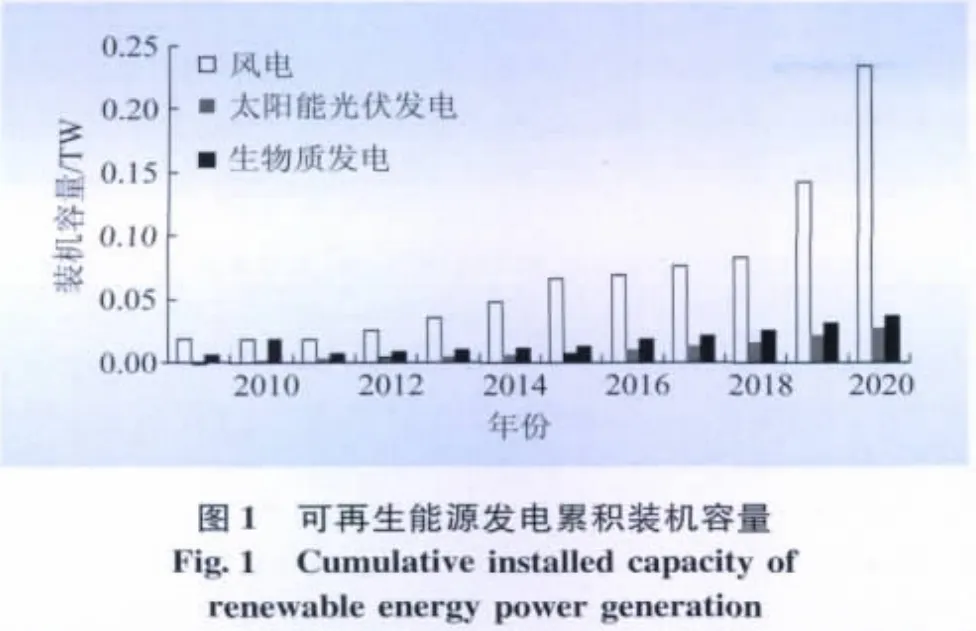
從圖1可看出:在最大利用情景下，2015年風電、太陽能光伏發電和生物質發電的累積裝機容量分別為65 999、8 000、12 210 MW，2020 年三者的累積裝機容量分別為233 321、26 680、35 506 MW。根據《新能源振興規劃》草案和《可再生能源中長期發展規劃》，2020年風電、太陽能光伏發電、生物質發電的預期裝機容量將達到150 000、20 000、30 000 MW。計算得到的最大利用情景下，3種可再生能源的總規模比規劃情景高出47.75%，風電、太陽能光伏發電和生物質發電的實際最大利用規模分別比規劃情景高出55.5%、33.4%、18.4%?？梢钥闯?，與生物質發電相比，風電和太陽能光伏發電還具有相當大的發展潛力。

從圖2可看出:生物質發電在初期得到了較快的發展，2009年增裝機容量達到了2 659 MW;而風電則主要是在2012年后得到了較快的發展，2012—2020年的平均年新增裝機容量達到了22 198 MW，并且呈現總體上漲的趨勢;太陽能光伏發電則保持相對平穩的增長態勢，平均年新增裝機容量達到了2 211 MW。

從圖3可看出，3種可再生能源發電的單位投資成本均呈現隨時間下降的趨勢。其中:由于太陽能發電在2010年的新增投資較大，使其單位成本出現較大的下降，從而為其后的規?；l展創造條件;2015年風電、太陽能發電和生物質發電的單位投資成本分別為0.49、1.33、0.58萬元/kW，2020年的單位投資分別為0.44、1.1、0.57萬元/kW。

4.2 主要不確定因素的敏感性分析

可再生能源發電最大規模的確定，受電網技術、宏觀投資比例等多方面因素的影響，而這些因素本身存在著較大的不確定性。因此，為了科學分析可再生能源發電的最大規模，對主要的不確定性因素進行了敏感性分析，結果如圖4、5所示。

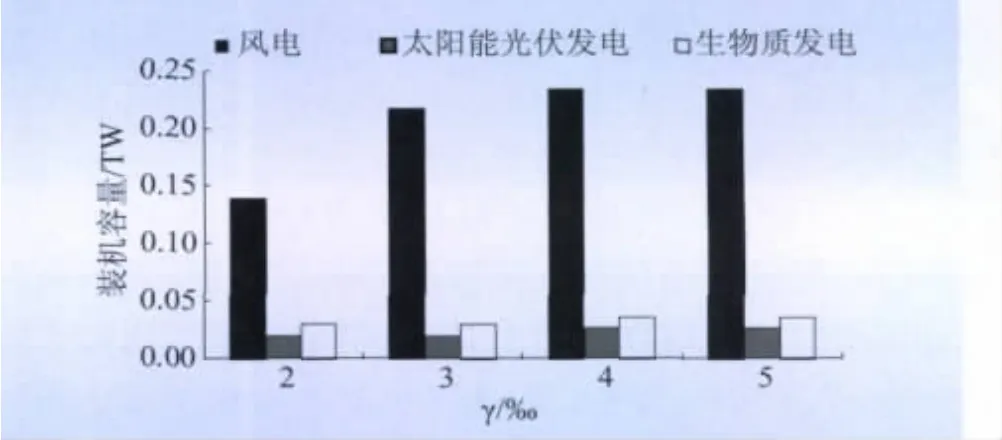
圖4 投資比例對2020年3種可再生能源最大發電規模的影響Fig.4 Impact of investment proportion on scales of renewable energy power generation in 2020

由圖4可看出:當γ從2‰上升到5‰時，可再生能源發電最大規模接近飽和;當γ小于1‰時，模型無法得到可行解。隨著投資比例的增加，風電得到了較大的發展，γ=2‰時，2020年風電累積裝機容量為139 049 MW;γ=4‰時，風電的累積裝機容量為23 321 MW，增長了67.7%;相比之下，太陽能光伏發電和生物質發電僅增長了33.4%和18.35%。

由圖5可看出:隨著μ的增加，可再生能源的最大發電規模趨向飽和;μ增大主要對風電和太陽能發電的2020年的累積裝機容量產生影響;μ=0.15時，風電和太陽能發電2020年的累積裝機容量分別為163 494、20 000 MW;μ≥0.25時，風電和太陽能發電2020年的累積裝機容量分別為233 321、26 680 MW。

5 結論

(1)2015年風電、太陽能光伏發電和生物質發電的累積裝機容量分別為65 999、8 000、12 210 MW，2020年三者的累積裝機容量分別為233 321、26 680、35 506 MW。

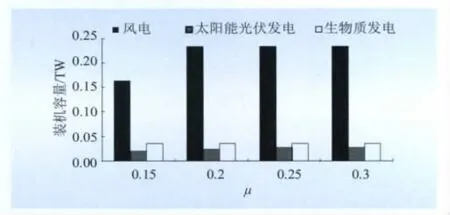
圖5 可再生能源上網比例對2020年3種可再生能源最大發電規模的影響Fig.5 Impact of grid connected proportion on scales of renewable energy power generation in 2020

(2)考慮到了發電成本的下降以及發電技術擴散效應的約束，3種可再生能源發電的年新增裝機容量呈現出了不同的特點。生物質發電在初期得到了較快的發展，而風電則主要是在2012年后得到了較快的發展，并且呈現總體上漲的趨勢，太陽能光伏發電則保持相對平穩的增長態勢。

(3)隨著可再生能源裝機容量的擴大，其對應的單位投資成本也呈現出下降的趨勢。其中，太陽能發電在初期的新增投資較大，使其單位成本出現較大的下降，從而可以為其后的規?；l展創造條件。2015年風電、太陽能發電和生物質發電的單位投資成本分別為0.49、1.33、0.58萬元/kW;2020年的單位投資分別為0.44、1.1、0.57萬元/kW。

(4)經濟約束主要對風電產生較大的影響，而對太陽能光伏發電和生物質發電影響較小。而可再生能源上網比例的增加，主要對風電和太陽能發電的2020年的累積裝機容量產生影響。

［1］盛明科，甘紀平.論低碳經濟發展背景下我國能源政策的失靈與矯正［J］. 吉首大學學報:社會科學版，2010，31(6):79-83.

［2］李虹，董亮，段紅霞.中國可再生能源發展綜合評價與結構優化研究［J］. 資源科學，2011，33(3):431-440.

［3］陶建格，薛惠鋒，能源約束與中國可再生能源開發利用對策［J］.資源科學，2008，30(2):199-205.

［4］Jain B C.Rural energy centres based on renewable-case study on an effective and viable alternative［J］. IEEE Trans on Energy Conversation，1987，2(3):329-335.

［5］Ramakumar R，Shetty P S，Ashenayi K.A linear programming approach to the design of integrated renewable energy systems for developing countries［J］.IEEE Trans on Energy Conversion，1986，1(4):18-24.

［6］Ashenayi K，Ramakumar R.IRES—a program to design integrated renewable energy system［J］.Energy，1990，15(12):1143-1152.

［7］Iniyan S，Jagadeesam T R.On the development of a reliability based optimal renewable energy model for the sustainable energy scene in India［J］.International Journal of Ambient Energy，1997，18(3):153-164.

［8］Iniyan S，Suganthi L，Samuel A A.Energy models for commercial energy prediction and substitution of renewable energy sources［J］.Energy Policy，2006，34(17):2640-2653.

［9］Argote L，Epple D.Learning curves in manufacturing［J］.Science，1990，247:920-924.

［10］Neij L.Use of experience curves to analyse the prospects for diffusion and adoption of renewable energy technology［J］.Energy Policy，1997，25(13):1099-1107.

［11］Neij L.Cost dynamics of wind power［J］.Energy，1999，24(5):375-389.

［12］Kuemmel B.Windpower econometrics［J］.Energy policy，1999，27(15):941-942.

［13］蒲曉璞，樊京春，王永剛.生物質能發電技術學習曲線和發電政策相互影響分析［J］.可再生能源，2009，27(3):84-88.

［14］葉金國，陳燕.我國能源產業系統的演化過程與混沌［J］.數學的實踐與認識，2005，35(8):5-10.

［15］Collantes G O.Incorporating stakeholders'perspectives into models of new technology diffusion:The case of fuel-cell vehicles［J］.Technological Forecasting and Social Change，2007，74(3):267-280.