圍長為8的QC-LDPC碼的顯式構造及其在CRT方法中的應用

張國華，孫蓉，王新梅

（西安電子科技大學 綜合業務網理論及關鍵技術國家重點實驗室，陜西 西安 710071）

1 引言

具有較大圍長的準循環低密度奇偶校驗(QC-LDPC)碼，由于具有線性時間可編碼、需要的存儲空間較小、譯碼性能優良等優點，目前得到人們越來越多的研究。借助于計算機搜索，人們提出了一些構造圍長大于6的QC-LDPC碼的準隨機方法[1,2]。這些基于搜索的方法雖然比較靈活,但是由于沒有解決碼的存在性問題，因此不可避免地存在構造失敗的可能性。相比而言，確定性方法可以直接給出校驗矩陣的顯式表達式，不存在構造失敗的可能性，但是確定性方法的設計具有很大的挑戰性，所以研究成果比較罕見。

(J,L) QC-LDPC碼的校驗矩陣是一個JL×的陣列，陣列中的每個元素都是一個PP×的循環置換矩陣（CPM）。到目前為止，構造圍長大于6的QC-LDPC碼的確定性方法只有幾種。對于列重 J為 3的情形，Tanner[3]基于群結構提出了一類圍長幾乎全部達到最大值12的(3,5)QC-LDPC碼（碼長為5P,P為素數且P-1可被15整除）；B.Vasic[4]基于最早序列提出了一類girth-8 (3,L)QC-LDPC碼;K.K.Liu[5]提出了一類girth-8 (3,L) QC-LDPC碼；張國華[6]受貪婪搜索啟發提出了一類girth-8 (3,L)QC-LDPC碼。對于列重為4的情形，目前已知的確定性構造方法只有一種，即K.K.Liu提出的一類girth-8 (4,L) QC-LDPC碼[7]。

本文提出了一種構造girth-8(4,L)QC-LDPC碼的新的確定性方法。這種方法構造出的碼允許碼長在某個門限之上以L為步進連續取值；更引人注目的是，這種碼的連續碼長最小值不僅比文獻[7]中碼的連續碼長最小值要小得多（僅為其3/4左右），而且幾乎可以達到目前利用計算機大規模搜索得出的碼長最小值。

本文組織如下：第2節描述了這種新碼的構造方法，并證明了其圍長特性；第3節比較了新構造方法和一些著名的搜索方法得到的碼長最小值；第4節提出了這種新碼的一種具體應用，即結合中國剩余定理(CRT)構造出一類圍長至少為8并且碼長非常靈活的合成QC-LDPC碼；第5節是結束語。

2 構造方法

(4,L) QC-LDPC碼的校驗矩陣可以表示為

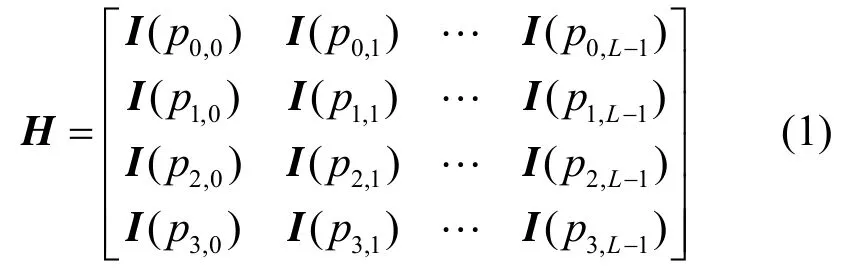
其中，I(x)表示一個受控于x的循環置換矩陣，具體定義與文獻[1]完全相同；為了便于論述和證明，下文使用m表示x的第一個索引標記，使用i, j, k表示x的第二個索引標記。本文按照如下方式配置pm,j(0≤m≤3,0≤j≤L-1)：

令上述配置下得到的矩陣用HD表示。定義HD中第r, s, t行(0≤r, s, t≤3)循環置換矩陣所構成的矩陣為HD(r, s, t)。首先證明一些性質和引理。

性質1 p2,L-1＜3L2/4。

性質2 若j＞i,則p2,j＞p2,i+p1,j。

證明 對j采用數學歸納法。首先考察j=i+1的情形。根據式(2)和式(3)，p2,i+1＞p2,i+(i +1)=p2,i+p1,i+1。現在假設p2,j-1＞p2,i+p1,j-1,則根據式(2)和式(3)有p2,j＞p2,j-1+1＞p2,i+p1,j。

引理1 對于任意整數P≥3L2/4,HD(0,1,2)中無4-環；對于任意整數P≥3L2/4+L-1,HD中無4-環。

證明 根據式(2)～式(4)和性質2，引理1很顯然成立。

引理2 對于任意整數P≥3L2/4，HD(0,1,2)的圍長為8。

證明 根據引理1，只需證明不存在6-環和證明存在8-環。假設HD(0,1,2)中存在6-環。則該環可用式(5)描述，其中，0≤i, j, k＜L互異。

情形1)j＞k, k≠0：式(5)變成p2,j=p2,k-p1,i+p1,jmod P，這是不可能的，因為根據性質2，式(6)成立。

情形2)j＞k, k=0：式(5)變成p2,j+p1,i-p1,j=0mod P，這是不可能的，因為根據性質2，式(7)成立。

情形3)j＜k：式(5)變成p2,k=p2,j+p1,i-p1,jmod P，這是不可能的，因為根據式(3)，式(8)成立。

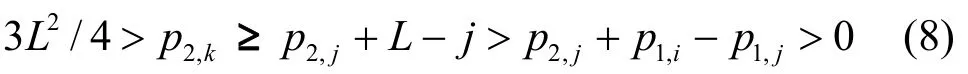
現在考慮8-環。根據式(2)，HD(0,1,2)中總是存在一個由式(9)描述的不依賴于P的8-環：

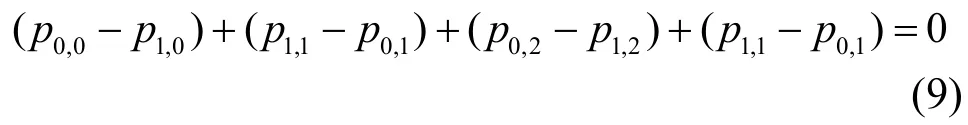
引理3 對于任意整數P≥3L2/4,HD(1,2,3)中無6-環。

證明 假設HD(1,2,3)中存在6-環。則該環可用式(10)描述，其中，0≤i, j, k＜L互異。

根據式(4)，式(10)變成(0-p1,i)+(p1,j-p2,j)+(p2,k-0)=0modP ，這意味著HD(0,1,2)中存在6-環。與引理1矛盾。

引理4 對于任意整數P≥3L2/4+L-1，HD(0,1,3)中無6-環。

證明 假設HD(0,1,3)中存在6-環。則該環可用等式(11)描述，其中，0≤i, j, k＜L互異。

根據式(4)，式(11)變成：

情形1)i＞k, k≠0：式(12)是不可能的，因為式(13)導致式(14)成立。

情形2)i＞k, k=0：式(12)變成p2,i+p1,i=p1,jmodP ，這是不可能的，因為根據性質1，式(15)成立。

情形3)i＜k, i≠0：式(12)變成p2,k=p2,i+p1,i-p1,jmod P，這是不可能的，因為根據式(3)，式(16)成立。

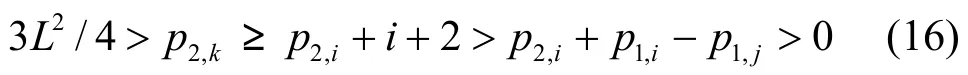
情形4)i＜k, i=0：等式(12)變成p2,k+p1,j=0modP，這是不可能的，因為式(17)成立。

引理5 對于任意整數P≥3L2/4+L-1,HD(0,2,3)中無6-環。

證明 假設HD(0,2,3)中存在6-環。則該環可用式(18)描述，其中，0≤i, j, k＜L互異。

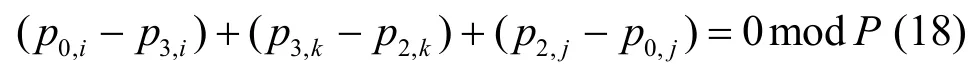
根據式(4)，式(18)變成：

情形1)i＞j,j≠0：式(19)變成p2,i=p2,j-，p1,i+p1,kmod P，這是不可能的，因為根據式(3)，式(20)成立。

情形2)i＞j,j=0：式(19)變成p2,i+p1,i=p1,kmod P，這是不可能的，因為根據性質1，式(21)成立。

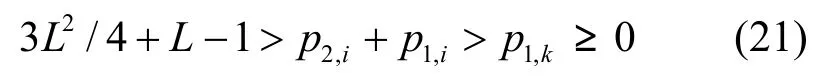
情形3)i＜j,i≠0：式(19)變成p2,j=p2,i+p1,i-p1,kmod P，這是不可能的，因為根據式(3)，式(22)成立。

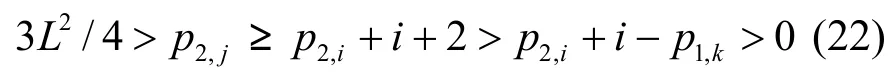
情形(4)i＜j,i=0：式(19)變成0=p2,j+p1,kmod P，這是不可能的，因為根據性質1，式(23)成立。

根據引理1～引理5可以得到定理1。

定理1 對于任意整數P≥3L2/4+L-1,HD的圍長均為8。

3 最小P值的比較

K.K.Liu最近提出了(4, L) QC-LDPC碼的一種確定性構造方法，對于任意2PL≥，該方法構造出的LDPC碼的圍長均為8。根據定理1，構造的girth-8(4,L) QC-LDPC碼的最小P值僅大約為K.K.Liu (4,L)QC-LDPC碼的最小P值的3/4。這說明，構造的girth-8 (4,L) QC-LDPC碼的碼長具有更加廣泛的取值范圍。

構造的girth-8 (4,L)QC-LDPC碼的最小P值甚至可以非常逼近基于計算機搜索的準隨機方法所得到的最小P值。Fossorier[1]和Sullivan[2]采用基于計算機搜索的準隨機方法，構造出了P值非常小的girth-8 (4,L) QC-LDPC碼。對于L=4～13,Fossorier 給出了使得girth-8 (4,L) QC-LDPC碼存在的最小P值。對于L=5～12,Sullivan給出了對應的搜索結果。圖1表明，對于L=5～13本文新方法給出的最小P值與上述2種準隨機方法給出的最小P值非常接近。

需要指出的是，雖然圖1中的3種方法得到的最小P值非常接近，但是本文的方法是確定性的，不需要借助于任何計算機搜索過程。此外，該方法所對應的最小P值是P允許連續取值的最小值：只要P不小于該最小值，相應LDPC碼的圍長就為8。對于Fossorier和Sullivan方法得到的最小P值而言，當P大于該最小值時LDPC碼的圍長不能保證必然為8，除非利用他們的搜索算法再次搜索出滿足girth-8條件的校驗矩陣。

圖1 3種方法得到的最小P值的比較

將HD的零空間對應的二元碼記為D-QCLDPC碼。下面首先分析D-QC-LDPC碼的理論價值。文獻[1]在III-B節中提出了一個相當難的問題（問題1）：如何給出使(J,L) QC-LDPC碼圍長至少為g的最小P值的解析結果？由定理1可知，只要P≥3L2/4+L-1就存在圍長至少為8的(4, L)QC-LDPC碼。顯然，該結論對于條件g=8，J=4下問題1的解決具有重要的理論參考價值。

另一方面，通過仿真發現，與文獻[1]搜索出的girth-8準隨機QC-LDPC碼相比，D-QC-LDPC碼在譯碼性能上沒有明顯優勢。但是，這并不說明D-QC-LDPC碼就沒有應用價值。相反，D-QC-LDPC碼作為一個基本模塊可以在其他的LDPC碼構造方法（例如CRT構造法）中發揮至關重要的作用。

4 基于CRT構造圍長至少為8的QC-LDPC碼

最近，中國剩余定理（CRT, Chinese remainder theorem）被應用到QC-LDPC碼的構造中[8,9]。利用CRT構造LDPC碼的優勢是，用若干個QC-LDPC短碼作為分量碼可以構造出QC-LDPC長碼，并且QC-LDPC長碼的圍長不小于所有分量碼的最大圍長。將array碼作為分量碼，文獻[8]利用CRT構造出了不含4環的QC-LDPC碼，文獻[9]利用CRT方法構造出了一類不含4環并且6環數量大大減少（但不能完全消除）的QC-LDPC碼。由于array碼的CPM尺寸為素數，因此這2種方法得到的QC-LDPC碼的碼長取值非常受限。本節將D-QC-LDPC碼作為分量碼，利用其CPM尺寸可以任意取值的優勢，基于CRT方法構造出一類不僅完全消除4環和6環，而且碼長非常靈活的QC-LDPC碼。

4.1 構造方法

根據CRT原理，利用一個不含6環的QC-LDPC短碼作為分量碼，可以構造出一系列不含6環的QC-LDPC長碼。D-QC-LDPC碼的圍長為8且CPM尺寸可以任意取值，因而非常合適作為CRT方法中的這種分量碼。

設J∈{3,4}，L是滿足L＞J的任意整數。令Pth(3,L)=3L2/4，Pth(4,L)=3L2/4+L-1。設P1≥Pth(J, L)。D-QC-LDPC碼的校驗矩陣H1是由P1×P1的CPM所組成的一個J×L陣列，其指數矩陣為。設P2是滿足gcd(P1, P2)=1的整數（gcd表示最大公約數），H2是由P2×P2的CPM所組成的一個J×L陣列，其指數矩陣為E(H2)=()。令P=P1P2，定義指數矩陣E(H)=(pm,j)，其中，，A1和A2是滿足gcd(A1, P1)=1、gcd(A2, P2)=1的2個任意正整數。根據CRT原理[9]，校驗矩陣H是由P×P的CPM所組成的一個J×L陣列矩陣，其圍長可以確保至少為8。

2方式下校驗矩陣H的圍長可能不同；即使圍長相同，長度等于圍長的短環數量也可能差別很大。下面提出一種選擇指數矩陣E(H2)的啟發式策略，以使校驗矩陣H的圍長盡可能大，并且短環數量盡可能小。

1)指數矩陣E(H)的首行首列元素初始化為0，即p0,j=0(0≤j≤L -1),pm,0=0(0≤m≤J -1)，其余元素初始化為∞。

2)按 照p1,1,…,pJ-1,1,p1,2,…,pJ-1,2,…,p1,L-1,…,pJ-1,L-1的順序，依次確定。確定的策略是在0至P2-1中選擇使當前H圍長最大的元素。如果有多個元素同時滿足該條件，可以隨機或按照固定方式選擇其中一個。這里采用固定方式，即選擇最小元素。

4.2 例子與仿真

相對于高碼率的LDPC碼而言，構造性能優良的中低碼率LDPC碼通常會更困難。例如，W E.Ryan和S.Lin在系統總結目前LDPC碼構造進展的最新專著《Channel Codes: Classical and Modern》[10]中所給出的絕大多數LDPC碼舉例均對應于高碼率(大于0.75)，只有很少的幾個例子對應于中低碼率(0.5及其以下)。下面利用4.1節所述方法構造了2個設計碼率為0.5的合成QC-LDPC碼。為了對新合成碼的性能作出客觀評價，選擇2種比較基準。第一種比較基準是1/2碼率條件下的Shannon限(0.188dB)。第二種比較基準是文獻[10]中設計碼率為0.5且碼長與新合成碼最為接近的LDPC碼。

例1 選擇P1=29,P2=7,A1=19,A2=2。根據4.1節構造方法，得到了校驗矩陣H的指數矩陣E(H)：

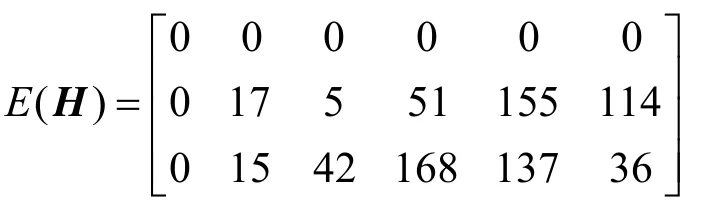
經驗證，校驗矩陣H的圍長為10。校驗矩陣H的CPM維數為(29×7)×(29×7)=203×203。對應的合成碼碼長為203×6=1218、碼率為0.5016。在進行譯碼仿真時，和積譯碼算法的最大迭代次數設定為80。在BER=10-6時，譯碼性能距離Shannon限僅2.43dB(如圖2所示)。文獻[10]中Example 11.8利用基于RS碼特殊子集的方法構造了一個碼長為1488、碼率為0.502的QC-LDPC碼，在BER=10-6時該碼的譯碼性能距離Shannon限為3.5dB。新合成碼比Example 11.8碼的性能改善了約1.07dB。

例2 選擇P1=64,P2=7,A1=21,A2=2。根據4.1節所述構造方法，得到了校驗矩陣H的指數矩陣E(H)：

經驗證，校驗矩陣H的圍長為8。校驗矩陣H的CPM維數為(64×7)×(64×7)=448×448。對應的合成碼碼長為448×8=3 584、設計碼率為0.501 1。在進行譯碼仿真時，和積譯碼算法的最大迭代次數設定為80。在BER=10-6時，譯碼性能距離Shannon限僅2.15dB(如圖2所示)。文獻[10]中Example 11.12.基于素域中的加法群方法構造了一個碼長為4 672、碼率為0.501的(4,8)QC-LDPC碼，在BER=10-6時該碼的譯碼性能距離Shannon限為2.05dB。雖然新合成碼比Example 11.12碼的性能略差一些，但是前者碼長要比后者碼長短1 088bit。這說明新合成碼的性能是非常優異的。

除了具有優異的譯碼性能，新合成碼的一個突出優勢在于碼長取值的靈活性。對于例1和例2所述的基于RS碼特殊子集的方法和基于素域中加法群的方法，其CPM尺寸與有限域的階數(為素數或素數的冪)存在密切關聯，因而CPM尺寸的選取不夠靈活。而4.1節提出的新方法CPM尺寸為P=P1P2，其中P1為滿足P1≥Pth(J, L)的任意整數，P2只要滿足gcd(P1, P2)=1即可，所以CPM尺寸的取值非常靈活。此外，新合成碼構造時不需要有限域知識背景，因此對于實際工程應用而言具有較大競爭力。

圖2 D-QC-LDPC碼作為分量碼利用CRT得到的合成QC-LDPC碼的性能曲線

5 結束語

本文提出了一種構造圍長為8的(4,L)QCLDPC碼的確定性方法。這類新碼的最小P值與Fossorier和Sullivan利用準隨機方法通過計算機大量搜索得到的最小P值非常接近。將新QC-LDPC碼作為分量碼，基于中國剩余定理構造出一類圍長至少為8且碼長取值非常靈活的合成QC-LDPC碼。在1/2設計碼率和中等碼長條件下的仿真結果表明，這類新的合成QC-LDPC碼在AWGN信道下具有優異的譯碼性能。顯然，本文設計的矩陣DH也可以用來構造圍長至少為8的多元QC-LDPC碼，具體構造細節和譯碼性能仿真將是近期的研究內容之一。

[1] FOSSORIER M P C. Quasi-cyclic low-density parity-check codes from circulant permutation matrices[J]. IEEE Trans on Information Theory, 2004, 50(8):1788-1793.

[2] O’SULLIVAN M E. Algebraic construction of sparse matrices with large girth[J]. IEEE Trans on Information Theory, 2006, 52(2):718-727.

[3] KIM S, NO J S,CHUNG H, et al. On the girth of tanner (3,5)quasi-cyclic LDPC codes[J]. IEEE Trans on Information Theory, 2006,52(4):1739–1744.

[4] VASIC B, PEDAGANI K, IVKOVIC M. High-rate girth-eight low-density parity-check codes on rectangular integer lattices[J].IEEE Trans on Communications, 2004, 52(8):1248-1252.

[5] LIU K K, FEI Z S, KUANG J M. Novel algebraic constructions of nonbinary structured LDPC codes over finite fields[A]. Proc 68th IEEE VTC Fall[C]. Calgary, Alberta, Canada, 2008. 1-5.

[6] 張國華, 陳超, 楊洋等. Girth-8 (3,L)-規則QC-LDPC碼的一種確定性構造方法[J]. 電子與信息學報, 2010,32(5): 1152-1156.ZHANG G H, CHEN C, YANG Y, et al. Girth-8 (3, L)-regular QC-LDPC codes based on novel deterministic design technique[J].Journal of Electronics & Information Technology, 2010, 32(5):1152-1156.

[7] LIU K K, FEI Z S, KUANG J M. Three algebraic methods for constructing nonbinary LDPC codes based on finite fields[A]. Proc 19th IEEE PIMRC[C]. Cannes, French Riviera, France, 2008.1-5.

[8] MYUNG S, YANG K. A combining method of quasi-cyclic LDPC codes by the Chinese remainder theorem[J]. IEEE Communication Letters, 2005, 9(9):823-825.

[9] LIU Y H, WANG X M, CHEN R W, et al. Generalized combining method for design of quasi-cyclic LDPC codes[J]. IEEE Communication Letters, 2008, 12(5):392-394.

[10] RYAN W E, LIN S. Channel Codes: Classical and Modern[M]. Cambridge University Press, 2009.