Keccak類非線性變換的差分性質研究

李倩男，李云強，蔣淑靜，路遙

(1. 信息工程大學 電子技術學院，河南 鄭州 450004；2. 中國科學院 光電研究院，北京 100094；3. 國防科學技術大學 計算機學院，湖南 長沙 410073）

1 引言

2010年12月10日，美國國家標準與技術協會（NIST）公布進入 SHA3競選算法[1～3]最后一輪的5個雜湊算法[4]，由Bertoni G、Daemen J和Peeters M等人設計的Keccak雜湊算法就是其中之一[5]。Keccak雜湊算法蘊涵著雜湊算法的最新設計理念[6,7]，對其編碼環節的系統分析具有重要的理論和應用價值。χ變換是Keccak壓縮函數中唯一的非線性環節，也是文獻[8～10]的算法所選用的非線性環節，文獻[11]中通過對Keccak的非線性環節進行改造，構造了新的非線性變換MiniKeccak。密碼算法抵抗差分分析的強度也一直是人們關注的問題，對密碼算法中的重要環節進行差分分析有助于分析整個密碼算法的抗差分分析攻擊的強度，也有助于對算法中的編碼環節進行更深刻的認識和把握。為了更好地應用Keccack類非線性變換編碼環節，本文將對其差分性質進行系統研究。

2 基本概念

則稱Y=f( X)為n元Keccak類非線性變換。

顯然，Keccak壓縮函數中χ變換是5元Keccak類非線性變換，MiniKeccak中的非線性變換是3元Keccak類非線性變換。

定義2 設(X, +)，(Y, +)是有限交換群，f: X→Y，α∈X,β∈Y,

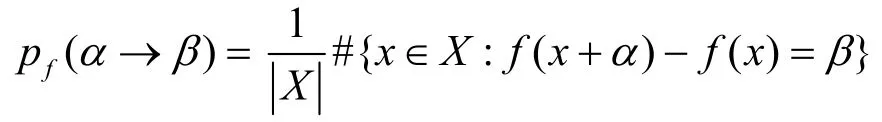
則稱pf(α→β)為f在輸入差為α條件下，輸出差為β的差分轉移概率，并稱α→β為f的一個差分對應，稱pf(α→β)為該差分對應的轉移概率。其中，和#{·}均表示集合·中的元素個數。

定義3 設X=(x0, x1,…,xn-1)∈GFn(2)為n維布爾向量，稱X=(x0, x1,…,xn-1)中的不為零的分量的個數為X的漢明重量，記做WH(X)。

3 差分性質分析

定理1 對于n元Keccak類非線性變換f，如果α, α′,β, β′∈，且β=f( x⊕α)⊕f( x)，＜α′, β′＞∈{＜a, b＞|a=(α＜＜j)且b=(β＜＜j ),0≤j＜n,j∈Z}， 那 么 差 分 轉 移 概 率pf(α′→β′)=pf(α→β)。

證明 當j=1，即α′=(α＜＜1)時，輸入、輸入差和輸出差從高位比特到低位比特依次可以表示為：x=(x0, x1,…,xn-1)，α=(α0,α1,…,αn-1)，β=(β0,β1,…,βn-1)，x′=(x0′, x1′,…,xn′-1)，α′=(α1,α2,…,αn-1,α0)， β′=(β0′,β1′,…,βn′-1)， 其 中 ，i∈{0,1,…,n-1}。那么輸出差β和β'的每一個比特的差分變換布爾函數表達式可以寫為

可知，當α′=(α＜＜1)，x′=(x＜＜1)時，有β′=(β＜＜1),f((x＜＜1)⊕(α＜＜1))⊕f((x＜＜1))=(β＜＜1)， 即f( x′⊕α′)⊕f( x′)=β′。 所 以 ，x′=(x＜＜1)∈。

pf(α′→ β′)==pf(α→β)，所以pf(α′→β′)=pf(α→β)。

假設j=m-1,(1＜m＜n, m∈Z)，pf(α′→β′)=pf(α→β)成立。j=m時的情況就是在j=m-1的基礎上繼續向左循環移動1位，由j=1時的結論，pf(α′→β′)=pf(α→β)也成立。所以，由數學歸納法可知定理1成立。

定理2 對于Keccak類非線性變換f，如果α, β, γ∈，pf(α→β)≠0，pf(α→γ)≠0，那么差分轉移概率pf(α→β)=pf(α→γ)。

為系數矩陣，設系數矩陣A的秩R(A)=r，X

0

為一個特解，那么所有的解可以表示為

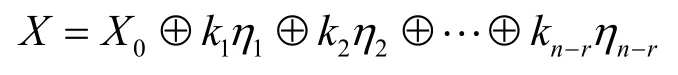
其中，kl∈{0,1}，l∈{1,2,…,n-r} ；，cm,n∈{0,1}，其中，m∈{1,2,…,n-r}，n∈{1,2,…,r} 。η1,η2,…,ηn-r為線性無關的基礎解系。

由于kl∈{0,1}，l∈{1,2,…,n-r}，所以方程組解的個數為2n-r個，||=2n-r。

又pf(α→β)==pf(α→γ)，所以定理2成立。

定理3 對于n(n≥3)元Keccak類非線性變換f，如果輸入差α，輸出差β，使β=f( x⊕α)⊕f( x)成立，且pf(α→β)≠0和1，那么。

證明 按照定理2的證明方法，pf(α→β)≠0時，將輸入、輸入差和輸出差從高位比特到低位比特依次可以表示為：x=(x0, x1,…,xn-1)，α=(α0,α1,…,αn-1)，β=(β0,β1,…,βn-1)，令yi=βi⊕αi⊕α(i+1)modnα(i+2)modn⊕α(i+2)modn， 其 中 ，xi,αi, βi,yi∈{0,1}，i∈{0,1,…,n -1}。={x| f( x ⊕α)⊕f( x)=β}，中元素個數||就是xi, yi∈{0,1}，i∈{0,1,…,n-1}的線性方程組解的個數。線性方程組的矩陣形式為

矩陣A的每一行和每一列都有輸入差的2bit，且同1bit出現在矩陣不同的行和列中，所以矩陣A中非零的行數越少，r越小；當矩陣A的每一行都有非零的元素時，r為最大值。顯然，當α=0，即A為零矩陣時，r=0；當α有1bit非零時，由于非零的比特出現在矩陣不同的行和列中，所以r=2；

當α有n-1和nbit非零時，矩陣A的所有行均非零。當α有n-1bit非零時，不妨設αi=0，

綜上，定理3成立。

定理4 對于n元Keccak類非線性變換f，如果 ＜α, β＞∈{＜(a＜＜j),(b＜＜j)＞|a=，其中*表示這個比特可以任意取0或1，那么。

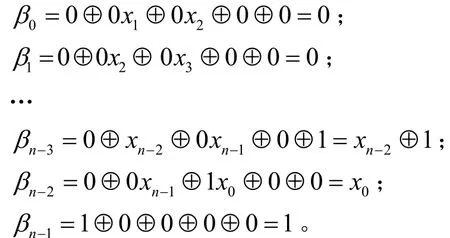
再由定理1，

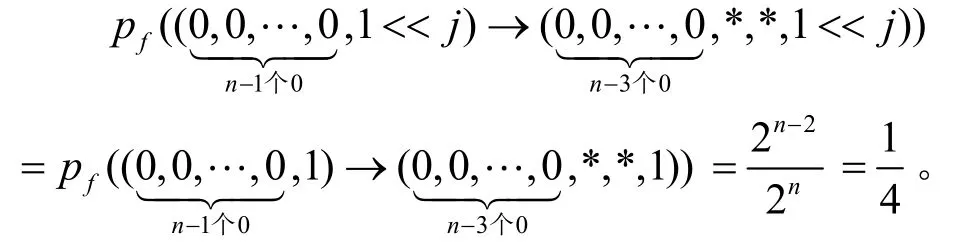
綜上，定理4成立。

定理5 對n元Keccak類非線性變換f，如果＜α, β＞∈{＜(a＜＜j),(b＜＜j)＞|a=或(·⊕1));或WH(a)=n,其中，*表示這個比特可以任意取0或1，·和(·⊕1)表示這2bit是互補的,0＜j≤n ,j∈Z}，則差分轉移概率

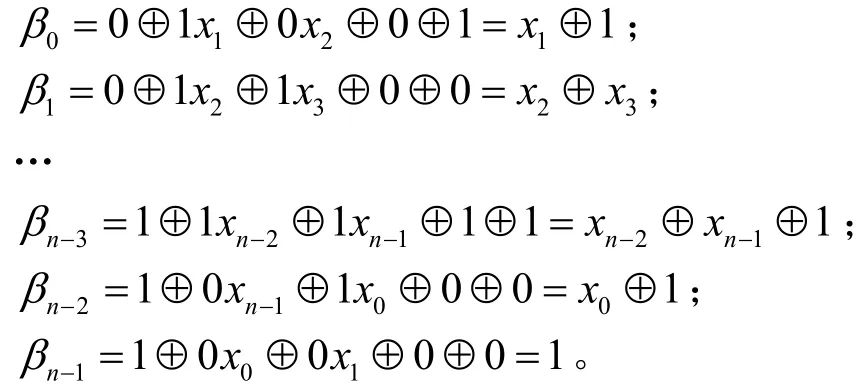
3) 輸入差α的漢明重量WH(α)=n,pf(α→β)≠0時，按照定理2的證明方法，將輸入、輸入差和輸出差從高位比特到低位比特依次可以表示為：x=(x0, x1,…,xn-1)，α=(α0, α1,…,αn-1)，β=(β0, β1,…,βn-1)，令yi=βi⊕αi⊕α(i+1)modnα(i+2)modn⊕α(i+2)modn，其中，xi,αi, βi,yi∈{0,1}，i∈{0,1,…,n-1}。，則方程組解的個數即為WH(α)=n時，中元素的個數||。為系數矩陣，系數矩陣的秩R(A)=r=n-1；所以||=2n-(n-1)=2，。

當WH(α)=n時，β的每個比特的布爾函數表達式為：

βi=x(i+1)modn⊕x(i+2)modn⊕1，其中，xi∈{0,1}，i∈{0,1,…,n -1}。

當n為偶數時：

所以，此時輸出差β的漢明重量為偶數。

同理可以證明，當WH(α)=n，n為奇數時，對于所有的WH(β)為奇數的輸出差β，都有pf(α→β)=。

綜上，定理5成立。

定理6 n元的Keccak類非線性變換f和n+1元的Keccak類非線性變換g有如下關系：對于n元Keccak類非線性變換f，輸入差α=(0,0,α0,α1,…,αn-3)，輸出差β=(β0,β1,…,βn-1)，對應的差分轉移概率為pf(α→β)；n+1元Keccak類非線性變換g，輸入差α′=(0,0,0,α0,α1,…,αn-3)，輸出差 β'=(0,β0,β1,…,βn-1)，差分轉移概率為pf(α′→β′)；那么pg(a′→β′)=pf(α→β)。其中,αi, βj∈{0,1},i∈{0,1,…,n-3},j∈{0,1,…,n -1}。

證明 當輸入x=(x0, x1,…,xn-1)、α=(0,0,α0,α1,…,αn-3)時，n元Keccak類非線性變換f對應的輸出差β每個比特的布爾函數表達式為：

當 輸 入x′=(x0′,x1′,x2′,…,xn′ ),α=(0,0,0,α0,α1,…,αn-3)時，n+1元Keccak類非線性變換g對應的輸出差β'每一個比特的布爾函數表達式為：

由 表 達 式 可 知 ， 當x0=x0′,xi=xi′+1(1≤i≤n-1)時，β=(β0,β1,…,βn-1)，β′=(0,β0,β1,…,βn-1)；x1′取值0或1對β′的值沒有影響。記，那么

pg( a′ →β′)==pf(α→β)，所以，pg(a′→β′)=pf(α→β)。

綜上，定理6成立。

4 結束語

雜湊函數Keccak中的壓縮函數的非線性變換已經被廣泛應用到很多密碼算法中，文獻[11]通過對其進行改造，提出了Minikeccak的非線性變換，并取得了良好的效果。為了更好地應用這一類非線性變換，本文建立了n元Keccak類非線性變換模型，并且分析了它的差分轉移概率性質，給出了最大的非平凡差分轉移概率和最小的非平凡差分轉移概率的結構和計數，給出了這類非線性變換相鄰變元間取相同差分轉移概率的結構。但是，還有許多Keccak類非線性變換模型的差分性質例如次大差分轉移概率、差分轉移概率為0的結構等情況，本文還沒有去研究分析。另外，對Keccak類非線性變換模型的Walsh譜值特性的研究將是下一個工作重點。

[1] NIST. Announcing request for candidate algorithm nominations for a new cryptographic hash algorithm (SHA-3) family[J]. Federal Register Notices 72, 2007, 212: 62212-62220.

[2] ANDREW R, RAY P, CHANG S J. Status Report on the First Round of the SHA-3 Cryptographic Hash Algorithm Competition[R]. Information Technology Laboratory National Institute of Standards and Technology, Gaithersburg, 2009.

[3] MELTEM S T, RAY P, LAWRENCE E B, et al. Status Report on the Second Round of the SHA-3 Cryptographic Hash Algorithm Competition. Computer Security Division[R]. Information Technology Labo-ratory National Institute of Standards-and Technology, Gaithersburg,2011.

[4] NIST. The SHA-3 Finalists candidates U S department of commerce national information service[EB/OL]. http://csrc. nist.gov. /groups/ST/hash/sha-3/Round3/submissions_round3. html.

[5] GUIDO B, JOAN D, MICHAEL P, et al. Keccak sponge function family main document[EB/OL]. http://csrc. nist.gov /groups/ ST /hash/sha-3 /Round1/submissions_round1. Html.

[6] 薛宇, 吳文玲, 王張宜. SHA3雜湊密碼候選算法簡評[J]. 中國科學院研究生院學報,2009, 26(5): 577-586.XUE Y,WU W L,WANG Z Y. Remarks of candidates hash algorithms for SHA3[J].Journal of CAS Postgraduates, 2009, 26(5): 577-586.

[7] 羅嵐,葉婭蘭,許春香等.在信念網模型下的 SHA3前五名算法注記[EB/OL].http://www.scienceet.cn/upload/blog/f-ile/2010/12/201012 1592436256375.pdf.LUO L, YE Y L, XU C X, et al. A note finalist5 of SHA3 at faithful network[EB/OL].http://www.scienceet.cn/upload/blog/file/2010/12/2010121592436256375.pdf.

[8] GUIDO B, JOAN D, MICHAEL P, et al. A belt-and-mill hash function[EB/OL]. http://radiogatun.noekeon.org.

[9] JOAN D, CLAPP C S K. Fast hashing and stream encryption with PANAMA[A]. Fast Software Encryption 1998 (S Vaudenay, ed)[C].1998. 60-74.

[10] JOAN D. Cipher and Hash Function Design Strategies Based on Linear and Differential Cryptanalysis[D]. Belgium: Katholieke Universities Leuven, 1995.

[11] EPHRAIM A. Sharing Nonlinear Gates in the Presence of Glitches[D].Enschede, Holland: University of Twente, 2010.