地鐵運營下鋼彈簧浮置板軌道減振分析

蔣崇達，雷曉燕

（華東交通大學(xué)鐵路環(huán)境振動與噪聲教育部工程研究中心，江西南昌330013）

進入新世紀(jì)以來的城市化發(fā)展，其規(guī)模和人口持續(xù)攀升，現(xiàn)有的地面交通遠遠滿足不了大中城市的人員流動，城市軌道交通憑借其運量大、準(zhǔn)時、安全可靠、候車環(huán)境舒適等優(yōu)勢得到了廣泛的運用。但伴之而來的地鐵運營所引發(fā)的環(huán)境振動問題成為難以治愈的頑疾。鋼彈簧浮置板軌道已在我國得到大量運用。以剛開通的杭州地鐵1號線為例，線路全長53 km，其中有4.597 km運用了鋼彈簧浮置板隔振技術(shù)。目前，各學(xué)者針對鋼彈簧浮置板軌道做了大量的研究[1-3]。多針對軌道本身進行了細致分析，對其引發(fā)的大地振動并未詳細計算。本文以有限元軟件ANSYS為平臺，建立了軌道-隧道-大地耦合有限元模型，列車荷載通過多體動力學(xué)軟件SIMPACK模擬。分別從頻域和時域的角度分析鋼彈簧浮置板軌道引發(fā)的大地振動。

1 計算模型及參數(shù)

1.1 列車荷載的模擬

采用多體動力學(xué)軟件SIMPACK建立的地鐵B型車的精細化MBS模型。車體、轉(zhuǎn)向架、輪對均為剛體模型，共42個自由度；空氣彈簧、軸向彈簧、橫向減震器、橫向止檔等均根據(jù)相應(yīng)力元單元模擬并連接上述剛體模型；輪對采用LM車輪踏面，車輛參數(shù)見文獻[4]。建立的單節(jié)B型車模型見圖1。軌道不平順選用美國6級譜，通過頻域法模擬后導(dǎo)入SIMPACK，采用軟件中09號不平順單元模擬。時間步長0.005 s，車速80 km·h-1。通過計算，第1輪對的垂向荷載（5 s）如圖2所示。

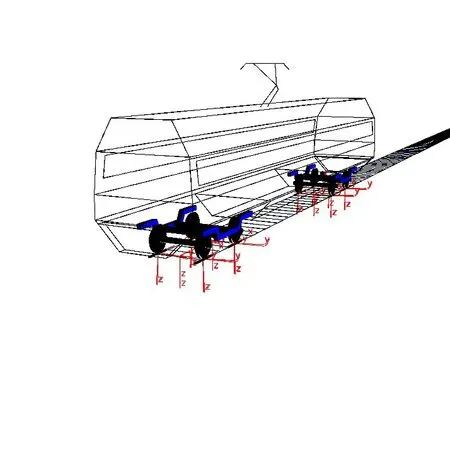
圖1 地鐵B型車MBS模型Fig.1 The subway B type car MBS model

1.2 軌道-隧道-大地計算模型

鋼軌類型為CHN60，采用考慮Beam188梁單元進行網(wǎng)格劃分；扣件采用Combin14彈簧阻尼單元，剛度50 kN·mm-1、阻尼5×104Ns·m-1（本文將整體道床考慮為單層軌道，取兩軌道扣件相同）；浮置板采用Shell63單元進行網(wǎng)格劃分，將其截面等效為面積相等的矩陣截面（厚0.4 m，寬3.2 m），采用C40混凝土；鋼彈簧支座只考慮豎向振動，采用Combin14彈簧阻尼單元進行網(wǎng)格劃分，剛度為6.9 kN·mm-1，阻尼為7.5×104Ns·m-1。隧道及土體參數(shù)來源于文獻[2]。襯砌采用Shell63單元，彈性模量為 3.5×104MPa，泊松比 0.25，密度2 500 kg·m-3。整體道床基礎(chǔ)厚度為0.635，浮置板基礎(chǔ)厚度為0.328，采用Solid45單元，彈性模量為2.85×104MPa，泊松比0.2，密度2 500 kg·m-3。土層采用Sol?id45單元，尺寸：豎向60 m、橫向100 m、縱向120 m。土體邊界采用等效粘彈性邊界。根據(jù)上述參數(shù)及單元，建立的計算模型見圖3。本文整體結(jié)構(gòu)的阻尼比綜合混泥土和土體[5]，取0.04。諧響應(yīng)分析時，系統(tǒng)阻尼比取0.04；瞬態(tài)分析時ANSYS采用瑞利阻尼[6]，本文瑞利阻尼系數(shù)取α=3.590 4、β=1.818 9e-4。

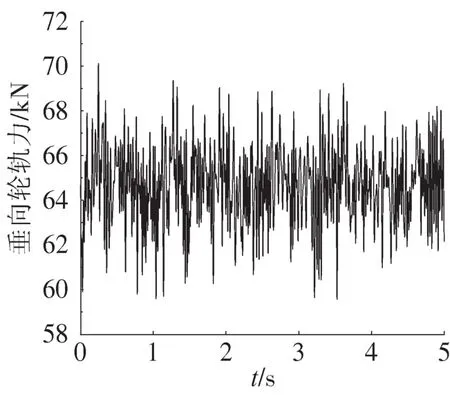
圖2 v=80km·h-1輪軌力Fig.2 v=80km·h-1wheel/rail force

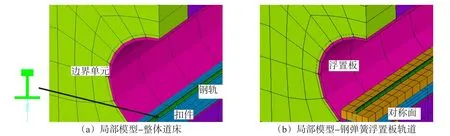
圖3 兩種軌道形式的軌道-隧道-大地計算模型Fig.3 Two kinds of orbital forms of orbit-tunnel-the earth calculation model

2 諧響應(yīng)分析

根據(jù)單自由度隔振原理可知[7]，固有頻率決定了結(jié)構(gòu)的隔振效果。基于ANSYS模態(tài)分析可知上述兩種軌道基頻分別為182 Hz，9.1 Hz；可以初步判斷整體道床僅對257 Hz以上的外力開始隔振，

鋼彈簧浮置板則對應(yīng)于12.86 Hz。事實上，軌道作為多自由度系統(tǒng)其含多個共振頻率，且軌道的受力形式為局部型加載。采用上述模型很難定量判斷其工作頻段及不利頻率。因此，有必要將軌道-大地作為耦合的大模型進行頻域計算，為工程實際提供參考依據(jù)。采用穩(wěn)態(tài)解掃頻技術(shù)可快速判斷結(jié)構(gòu)響應(yīng)與頻率的關(guān)系，進而判別各軌道隔振能力。本文，加載點取中心斷面處的鋼軌節(jié)點，荷載幅值為72 kN，頻段為0～100 Hz。經(jīng)計算，提取0，30，60，96 m結(jié)果，如圖4所示。

由圖4可以得出以下結(jié)論：

1）整體道床于0～100 Hz內(nèi)同樣有著較大的衰減，其實質(zhì)反映的是土體自身對外力的衰減；本文土質(zhì)中，最不利頻率為5 Hz左右，60 m處對20～40 Hz的外力有著較大的共振現(xiàn)象。

2）兩種軌道結(jié)果于13 Hz左右有一交叉點，大致為鋼彈簧浮置板基頻的1.414倍；若根據(jù)單自由度隔振理論，剛好為其工作頻段的開始。

3）對于13 Hz以內(nèi)，由于包含了鋼彈簧浮置板的基頻（9 Hz）故其結(jié)構(gòu)響應(yīng)要大于整體道床；共振現(xiàn)象隨著離軌道中心線距離的增大而減小并最終趨于相等；沿距離來看，30 m以內(nèi)的共振現(xiàn)象衰減比例更大。

4）對于大于13 Hz的頻段，鋼彈簧浮置板的結(jié)構(gòu)響應(yīng)明顯更小。60 m左右，由于土體自身的影響，鋼彈簧浮置板于20～40 Hz處也略有放大。

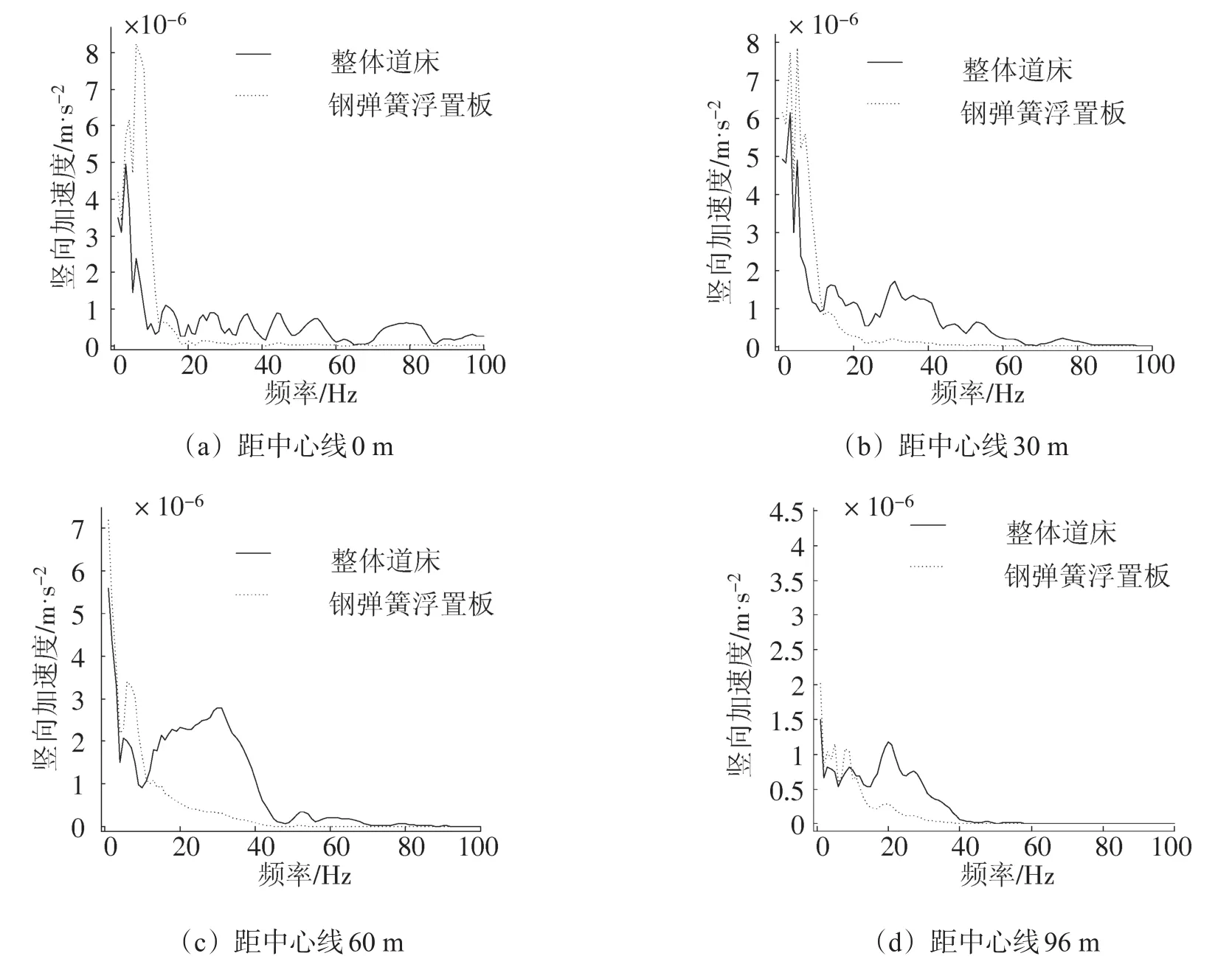
圖4 加速度響應(yīng)-激振頻率關(guān)系圖Fig.4 Acceleration response-vibration frequency relationship diagram

3 瞬態(tài)分析

前面采用的是定點同幅值諧荷載下的掃頻分析，而列車運行所引發(fā)的輪軌力在各個頻段上的幅值是不同的。故有必要進行時域計算，對比兩種軌道所誘發(fā)的大地振動。

3.1 振動評價指標(biāo)

采用振動加速度級La對振動水平進行評價[8]，計算方法如式（1）所示。

式中：La為振動加速度級，dB；arms為1/3倍頻程中心頻率對應(yīng)的振動加速度有效值，m·s-2；a0為基準(zhǔn)加速度，取10-6m·s-2

3.2 算例分析

考慮到模型較大，車速較低，列車荷載僅考慮2節(jié)車地鐵車輛。時間步長0.005 s，車速80 km·h-1。浮置板板厚考慮3種：0.3，0.5，0.7 m，分別對應(yīng)結(jié)構(gòu)固有頻率11.2，8.1，6.67 Hz。經(jīng)計算，輸出數(shù)據(jù)為距軌道中心線0，30，60，96 m的豎向加速度時程曲線。限于篇幅僅給出0 m處的時域結(jié)果，結(jié)果如圖5所示。

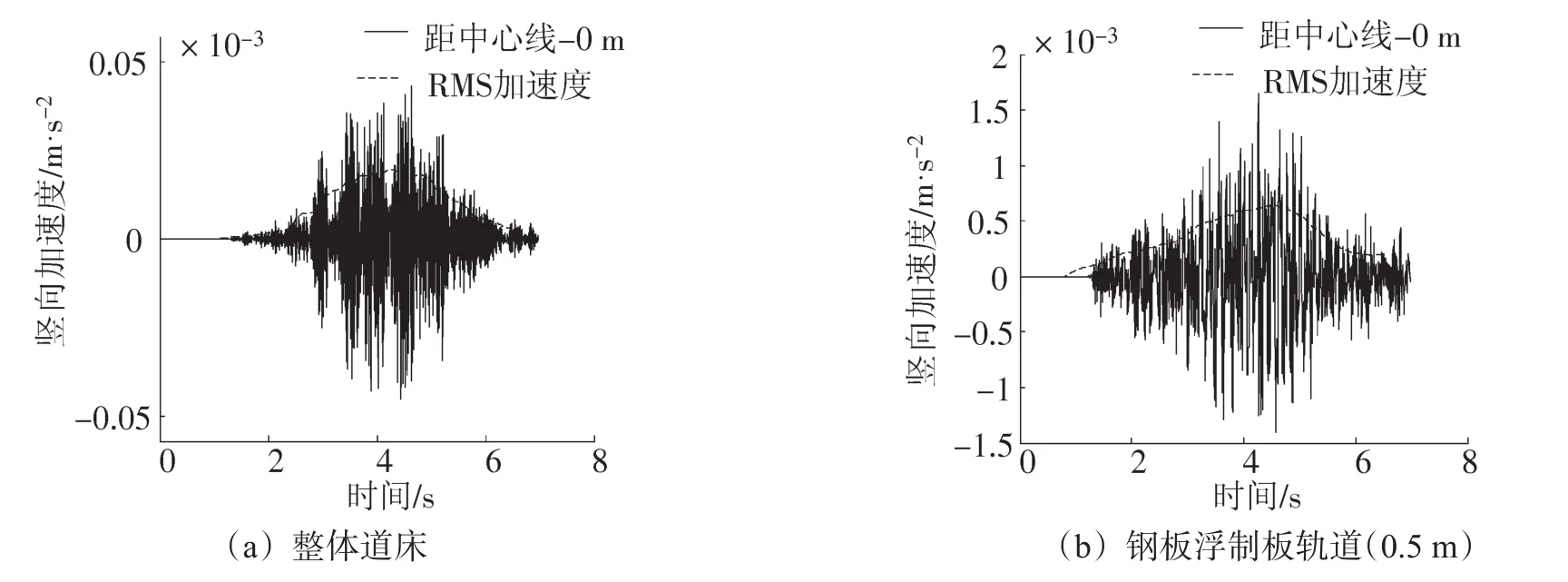
圖5 地表振動加速度對比（0 m）Fig.5 The surface vibration acceleration contrast（0 m）

根據(jù)圖5均方根加速度（root mean square，RMS）可知，采用鋼彈簧浮置板軌道可以大大的降低列車誘發(fā)的大地振動。從圖形來看，鋼彈簧浮置板軌道比整體道床更容易事先振動，靠近襯砌附近的土體可以更多的參與振動進而將能量擴散。

對4個拾取點的振動時程進行1/3倍頻程分析，以分析各頻段內(nèi)兩種軌道引起的地表振動水平分布，結(jié)果如圖6所示。

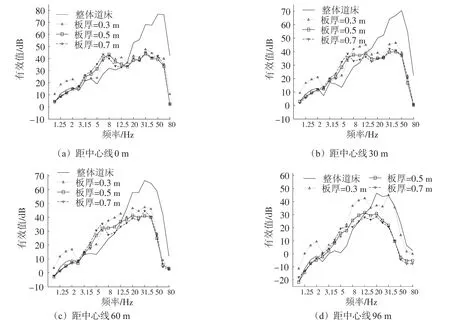
圖6 地表振動加速度1/3倍頻程對比Fig.6 The surface vibration acceleration 1/3 octave contrast

圖6中橫坐標(biāo)的增加幅度為2Λ1 3。由圖6可以得出以下結(jié)論：

1）采用整體道床時，列車運行誘發(fā)的大地振動主頻大致分布于30～60 Hz范圍內(nèi)。由于土體的作用，一方面高頻振動得到了部分衰減，另一方面在30～60 Hz的共振區(qū)域內(nèi)隔振效果欠佳。

2）當(dāng)浮置板軌道板厚大于0.3 m后，在小于3 Hz的頻段內(nèi)，兩種軌道誘發(fā)的振動水平相當(dāng)。

4）降低浮置板軌道的固有頻率，可以擴大浮置板軌道的工作頻段，從而實現(xiàn)較好的低頻隔振。

5）整體道床沿線路方向的衰減要大于鋼彈簧浮置板軌道。因為在靠近線路中心處，鋼彈簧浮置板軌道能更好的將能量均攤。

6）浮置板軌道的最大衰減量可達40 dB，發(fā)生在距軌道中心線0 m處50 Hz的頻率。隨著距軌道中心線距離的增大，衰減趨于穩(wěn)定，達到25 dB左右。

4 結(jié)論

本文通過數(shù)值計算，可以得出以下結(jié)論：

1）建立軌道-大地耦合模型，采用諧響應(yīng)的分析方法。可定量的判斷軌道的工作頻段及不利頻率，進而為后面時域分析提供依據(jù)。

2）由于土體和軌道的共同作用，鋼彈簧浮置板軌道基本上僅受基頻引發(fā)的共振放大。那么對其設(shè)計的重點應(yīng)放在保證結(jié)構(gòu)安全的情況下如何降低系統(tǒng)1階固有頻率，可對不同方案在中高頻的略微隔振差別不予考慮。

3）鋼彈簧浮置板基頻處的共振現(xiàn)象影響范圍不大，對于3 Hz～基頻的頻段很難得到衰減。由于土體的作用，30～60 Hz頻段仍有共振現(xiàn)象。土體本身特性對地表振動分布起到了較大影響。總體看來，采用鋼彈簧浮置板軌道可以很好對中高頻外力進行衰減，最大衰減可達40 dB。

4）經(jīng)過比對，鋼彈簧浮置板減振效果顯著，值得大力推廣應(yīng)用。

[1] DEYUN DING，WEINING LIU.Low frequency vibration tests on a floating slab track in an underground Laboratory[J].Journal of Zhejiang University-SCIENCEA，2011，12（5）：345-359.

[2]孫曉靜.地鐵列車振動對環(huán)境影響的預(yù)測研究及減振措施分析[D].北京：北京交通大學(xué)，2008：118-143.

[3]吳天行.軌道減振器與彈性支承塊或浮置板軌道組合的隔振性能分析[J].振動工程學(xué)報，2007，5（2）：489-493.

[4]趙雷.B型城市軌道交通車輛轉(zhuǎn)向架低動力作用仿真研究[D].北京：北京交通大學(xué)，2010：21-22.

[5]黃宗明，白紹良.結(jié)構(gòu)地震反應(yīng)時程分析中的阻尼問題評[J].地震工程與工程振動，1996，12（2）：95-105.

[6]克拉夫，彭津.結(jié)構(gòu)動力學(xué)[M].北京：科學(xué)出版社，1981：183-186.

[7]丁文鏡.減振理論[M].北京：清華大學(xué)出版社，1988：18-28.

[8]劉騰，雷曉燕.高速鐵路沿線地面環(huán)境振動特性的實測與分析[J].華東交通大學(xué)學(xué)報，2011，28（4）：19-22.

[9]雷曉燕.有限元法[M].北京：中國鐵道出版社，2000：30-71.