管路支架諧波響應特性分析及簡化模型的建立

王永勝，張京偉，吳崇健，吳聲敏

(中國艦船研究設計中心，湖北 武漢 430064)

0 引言

管路支架是船舶管路系統的一個重要組成部分。在1艘船舶中，管路支架的數量較大且種類較多。在對管路系統進行動力學分析時，如果對管路支架進行實體建模，會使計算成本過大。Lennart G.Jansson和LING Fu-zeng在文獻 ［3］中指出，在以往的工程經驗中，對支架的建模和計算往往占據了整個管道系統分析預算的1/3。由此可以看出，建立合適的管路支架模型對于實際工程的重要意義。文中還總結了目前常用到的3種支架模型嘗試:①把支架總體看成剛性約束;②把支架看成彈性約束;③在滿足某種標準時看成剛性約束，而其他情況下就要考慮其彈性因素。其中把支架看成彈性約束時，往往是采用單自由度彈簧和阻尼來代替，而忽視了支架本身質量的影響。本文將首先對船舶中較常見的管路支架進行頻域分析，然后在此基礎上提出二自由度簡化模型。

1 管路支架的頻域特性分析

1.1 研究對象

由于管路支架的種類較多，這里選用1種船舶中較常見的管道之間為55 mm的馬腳型管路支架作為研究對象。這種管路支架根據橡膠材料和卡箍的關系又可分為2類:一類是橡膠與卡箍相互獨立;另一類即橡膠與卡箍黏接在一起或卡箍包裹在橡膠里面，參見圖1。

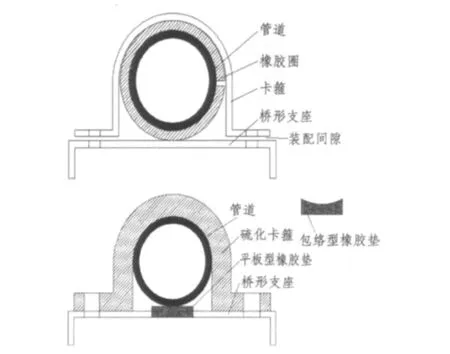
圖1 2種類型的馬腳型管路支架結構Fig.1 Schematic diagram of two kinds of piping supports

圖1中的2種管路支架有個共同點，即由多個構件組成，構件與構件之間存在著接觸關系，整個結構通過螺栓預緊來實現緊固。

1.2 頻域分析

利用Ansys軟件中的諧響應分析模塊對管路支架進行頻域特性分析。這里選用圖1中第2種管路支架作為計算對象，這種管路支架又叫硫化馬腳，其卡箍由鋼片和包裹在外面的硫化橡膠組成。Ansys提供了3種諧響應分析方法［2］:完全法、縮減法和模態疊加法。3種方法各有優劣，本文選用模態疊加法進行分析。這是因為研究對象是一個多構件結構，包含接觸非線性 (在小變形情況下可忽略材料非線性)，不同構件通過螺栓預應力緊固在一起。這一過程可通過預應力計算來實現，而模態疊加法支持預應力效果，然后在此基礎上進行含預應力的諧響應分析。

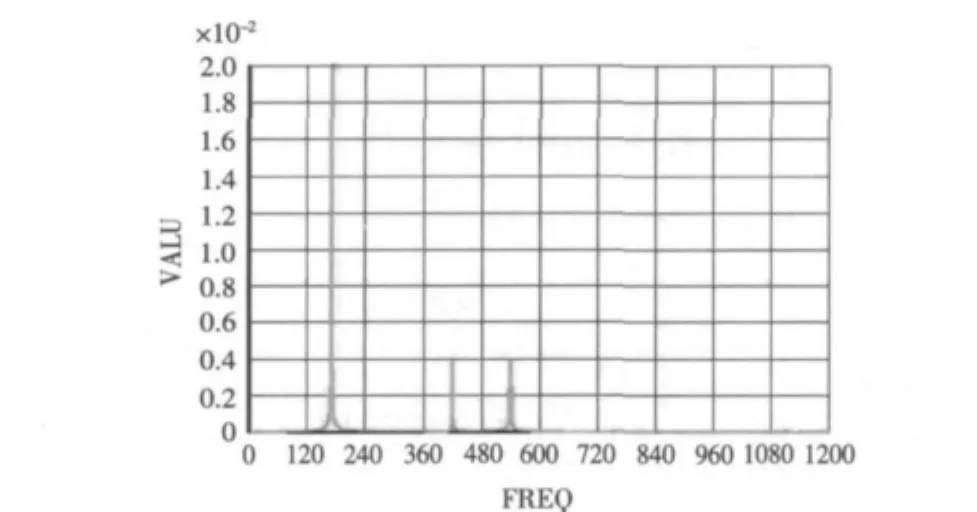
圖2 無阻尼時管的垂向位移響應曲線Fig.2 Displacement response curve of pipe in the vertical direction without damping

先不考慮阻尼，為減小計算成本，管長取0.1 m，結構用體單元模擬，管道端面設置對稱約束，在管道兩端分別加載幅值為100 N，頻率范圍0～2000 Hz的垂向或橫向載荷進行計算。加載垂向載荷時，計算得到頻域內管的垂向位移響應曲線如圖2所示。

由圖2可知，在頻率0～1200 Hz范圍內，管道有三階模態被激發，分別對應的頻率為170.19，420.15，539.52 Hz，選取被激發的前二階模態，列出其振型如圖3所示。

圖3 垂向被激發的前二階模態振型Fig.3 The first two excited modal shapes in the vertical direction

管道除了受到垂向激勵的作用外，還可能受橫向激勵的作用。在加載橫向激勵作用下管道的橫向位移曲線如圖4所示。

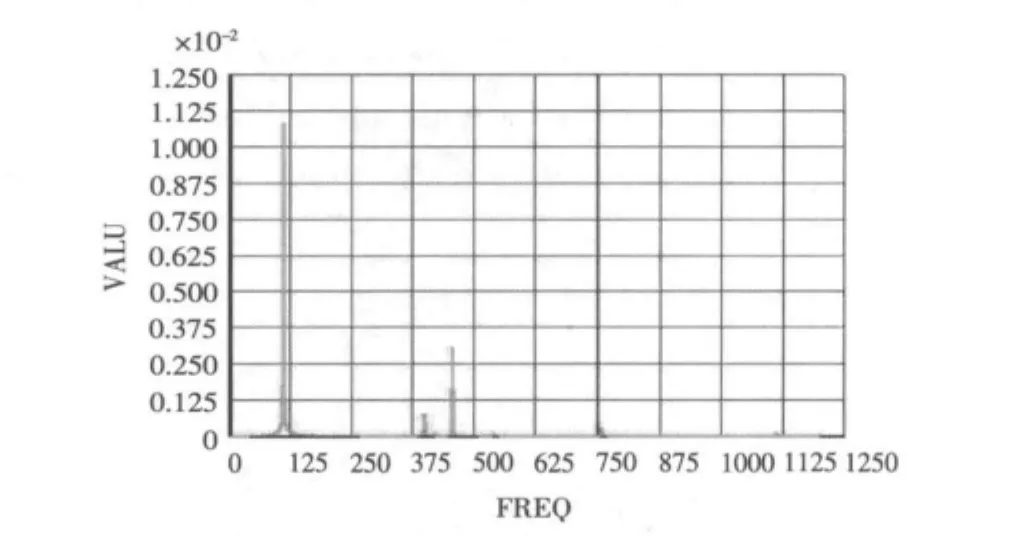
圖4 無阻尼時管的橫向位移響應曲線Fig.4 Displacement response curve of pipe in the horizontal direction without damping

圖4中被激發的前三階模態對應的頻率分別為110.81，398.58，456.08 Hz，其中第一和第三階被激發的響應比較明顯，列出這二階對應的振型如圖5所示。

由上面的分析可知，管道的垂向和橫向位移響應除由主振型被激發產生的主峰值外，還有由橡膠卡箍固有振型被激發產生的從屬峰值，這也說明卡箍與支座的固有特性會對管道響應產生影響，在建立簡化模型時必需要考慮到這點。

圖5 橫向被激發的二階模態振型Fig.5 The first two excited modal shapes in the horizontal direction

實際上，由于管路支架包含橡膠材料，因此在分析中應該考慮阻尼的影響，通過設置一定的材料阻尼計算得到的管道垂向和橫向位移響應如圖6所示。

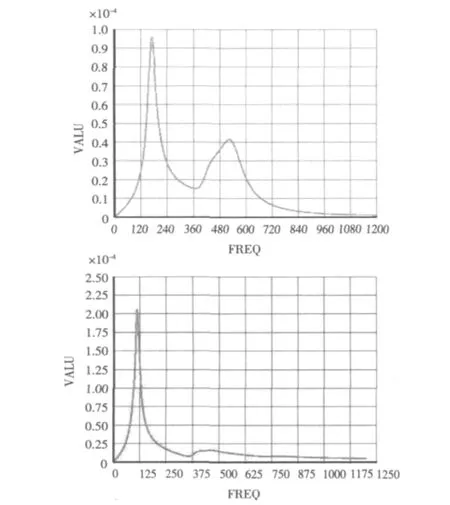
圖6 含阻尼時管道的垂向和橫向位移曲線Fig.6 Displacement response curves of pipe in both directions with damping

與前面無阻尼時管的位移響應曲線相比，由于阻尼對振動的衰減作用，有阻尼位移響應曲線的各個峰值明顯降低。另外，與無阻尼響應曲線相比，圖6中曲線的共振峰個數減少了，特別是無阻尼響應曲線中的第2和第3個共振峰在有阻尼的情況下合成了1個共振峰，這是因為二者對應頻率相近，峰值還來不及衰減就進入了下1個共振峰。因此在對硫化馬腳建立簡化模型時不能簡單地用單自由度模型代替，應至少包含2個自由度。

2 管路支架簡化模型的建立

在以往對管路系統的分析中，一般都是用單自由度的彈簧—阻尼系統來模擬管路支架［4］。這樣的處理方式在一定程度上可以滿足工程分析的要求，但它忽視了支架本身固有特性的影響。由前面的分析可知，不考慮阻尼時，管道在垂向和橫向2個方向上的響應在低頻范圍內存在多個共振峰。由于影響管道響應的主要是低階模態，因此在建立簡化模型時可以只取前面幾個共振峰而忽略掉高階共振峰的影響，這里取2個共振峰，如果第2和第3個峰值比較接近，則將二者合并，組成1個共振峰。這樣含2個共振峰的響應曲線與二自由度系統的響應曲線相似，因此可以考慮在2個方向分別用二自由度質量－彈簧－阻尼系統來簡化管路支架，具體模型如圖7所示。

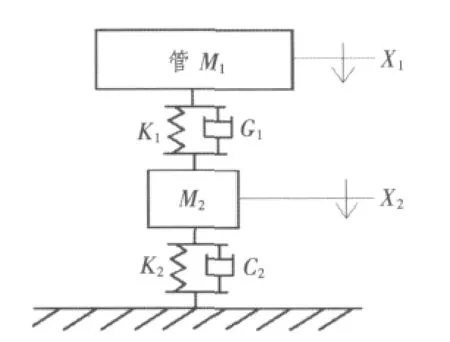
圖7 二自由度簡化模型圖Fig.7 Two-degree-of-freedom modals

不考慮阻尼時，上面的二自由度系統包含M1，K1，M2，K2共4個參數。M1已知，為0.1 m長管的質量，這里等于0.386 kg;M2是中間質量塊的質量，它并不是簡單地等于管路支架的質量。因此，4個參數中有3個未知，欲得到這3個未知參數，則必須要有3個方程。二自由度系統具有二階固有頻率，若要用它來模擬實際的管路支架，則必須使這二階固有頻率等于前面無阻尼諧響應分析中被激發的前二階模態對應的頻率，據此可以得到2個方程。據振動理論，無阻尼二自由度系統的運動微分方程為

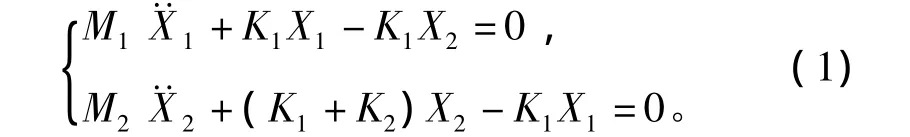
求解特征方程可得到系統的固有頻率

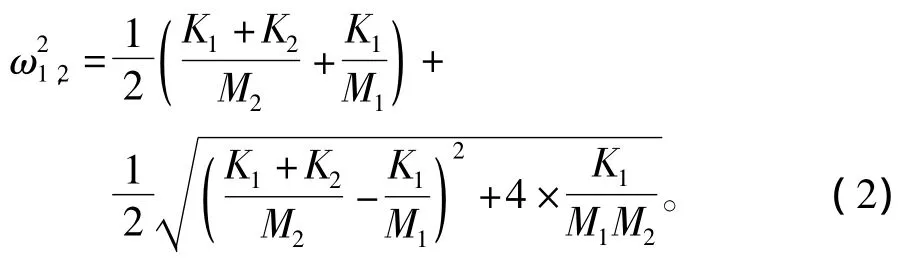
已知ω1和ω2，這樣就得到了2個方程，另外還需1個方程就可以求得3個未知參數。第3個方程可以通過2種方式來建立，一種是通過模態振型來確定，對于上面的兩自由度系統，當它按某一固有頻率作簡諧同步運動時，M1和M2運動的振幅之比是一個確定的量，由系統本身的物理性質所決定［1］，這個比值為

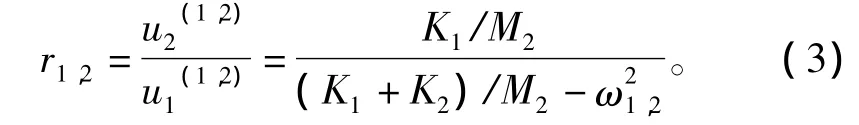
式中:u1和u2分別為M1和M2的運動幅值，右上角括號內的數字代表階數;r1，2分別為M1和M2在第一階固有頻率和第二階固有頻率時的振幅之比，這個比值可以從前面管路支架無阻尼諧響應分析的結果中得到。假設u1為管路第一階的運動幅值，u2也取支架上某一點的第一階的運動幅值，這樣就構成了第3個方程。

另一種方法根據模態質量的性質來建立第3個方程。模態質量可以理解為結構實際參與某一階模態運動的質量，因為在結構中各部分參與模態運動的程度是不一樣的，所以模態質量一般不是已知的結構質量。在Ansys提供的模態分析中能夠通過歸一化處理提取任一階模態質量，因此也可以提取本文關心的某一個被激發的振型對應頻率的模態質量 M'(r)，然后代入式(4)得到第3個方程。

對于一個多自由度度系統，其模態質量M(r)可由下式得到:

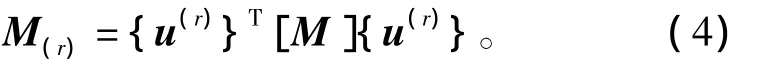
式中:{u(r)}為模態矢量矩陣;［M］為系統質量矩陣，將它進行歸一化處理可得到M'(r)。對于本文關心的二自由度系統，可取第一階模態質量，它對應于實體模型中第1個被激發的固有模態對應的模態質量M'(1)，可得到以下方程:

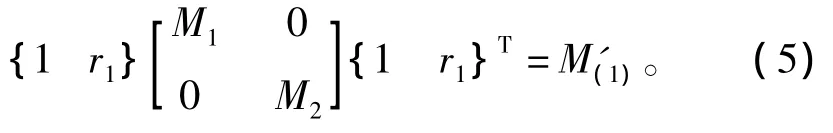
式中，r為二自由度系統第一階模態振型的幅值之比，可由式(3)得到。M'(1)由軟件計算給出，這樣就確立了第3個方程，由這3個方程就可以求得3個未知參數了。下面根據前面的分析分別確定2種管路支架簡化模型的各個參數。

在確定硫化馬腳型支架簡化模型的參數時，這里采用第2個方法即提取模態質量來建立第3個方程。考慮到圖2中管道垂向被激發的三階頻率中第二、三階頻率比較接近并且與第一階相距較遠，故可將二者合并成1個頻率，取中間某個值，這樣得到簡化模型的前二階頻率為170.19，456 Hz，頻率為170.19時從Ansys計算中提取的模態質量為0.4684 kg，這樣代入3個方程解得垂向模型的K1，M2，K2分別為9.21e5，0.3037，1.2e6(國際單位制);另外，由圖4位移響應的特點，取第一和第三階被激發的頻率110.81，456.08 Hz作為簡化模型的二階頻率，第一階頻率對應的模態質量為0.525 kg，將它們代入3個方程解得橫向模型的K1，M2，K2分別為9.7451e5，0.2114，3.2842e5。

以上建立了該類型支架的簡化模型。

3 簡化模型的驗證

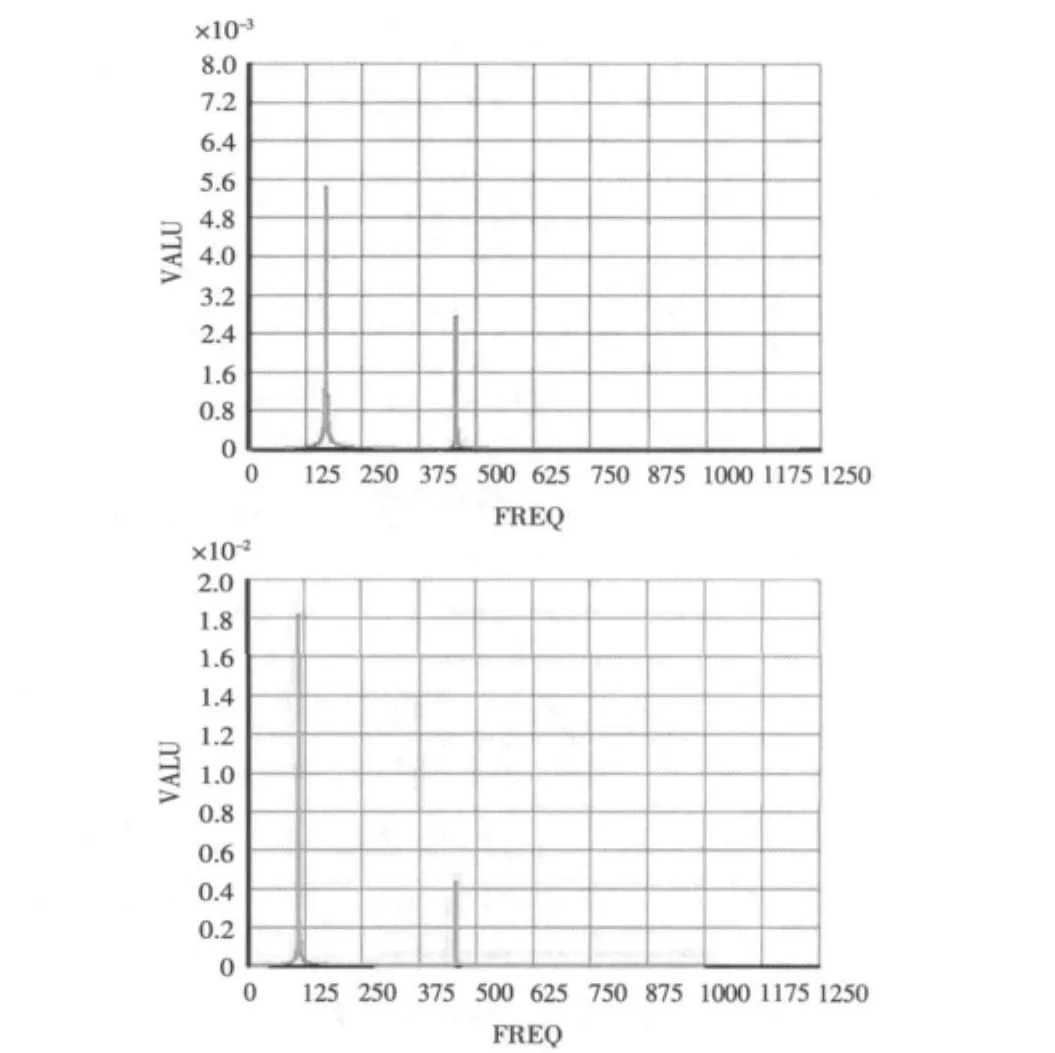
圖8 支架簡化模型管的垂向和橫向位移曲線Fig.8 Displacement response curves of pipe in both directions of simplified model

為驗證簡化模型的可靠性，利用Ansys軟件對該簡化模型分別進行檢驗計算。其中管道用梁單元beam188，截面尺寸和長度與前面的實體模型相同，管路支架用2組彈簧阻尼單元combin14和質點單元模擬，施加相同的激勵和約束條件。不考慮阻尼時，計算得到支架簡化模型中管道的垂向和橫向位移曲線，如圖8所示。

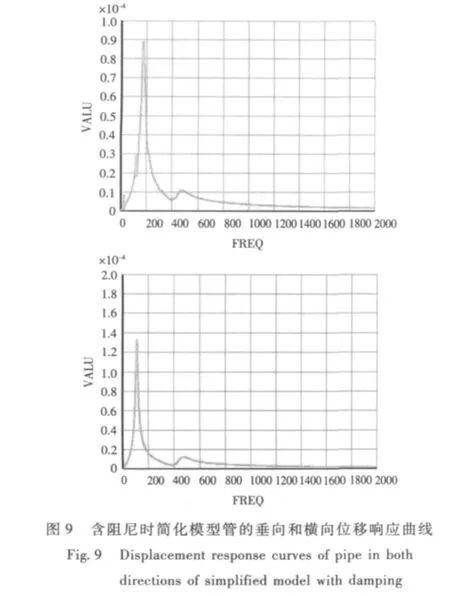
將圖8與圖6對比，支架簡化模型中管道在2個方向的位移響應被激發的頻率與實體模型相近，只是響應的幅值有差別，但這可以通過調整阻尼來消除。假設支架固定在一塊厚2 cm，邊長為2 m的簡支鋼板上，通過設置合適的單元阻尼和材料阻尼，進一步求得支架簡化模型中管道響應曲線如圖9所示。

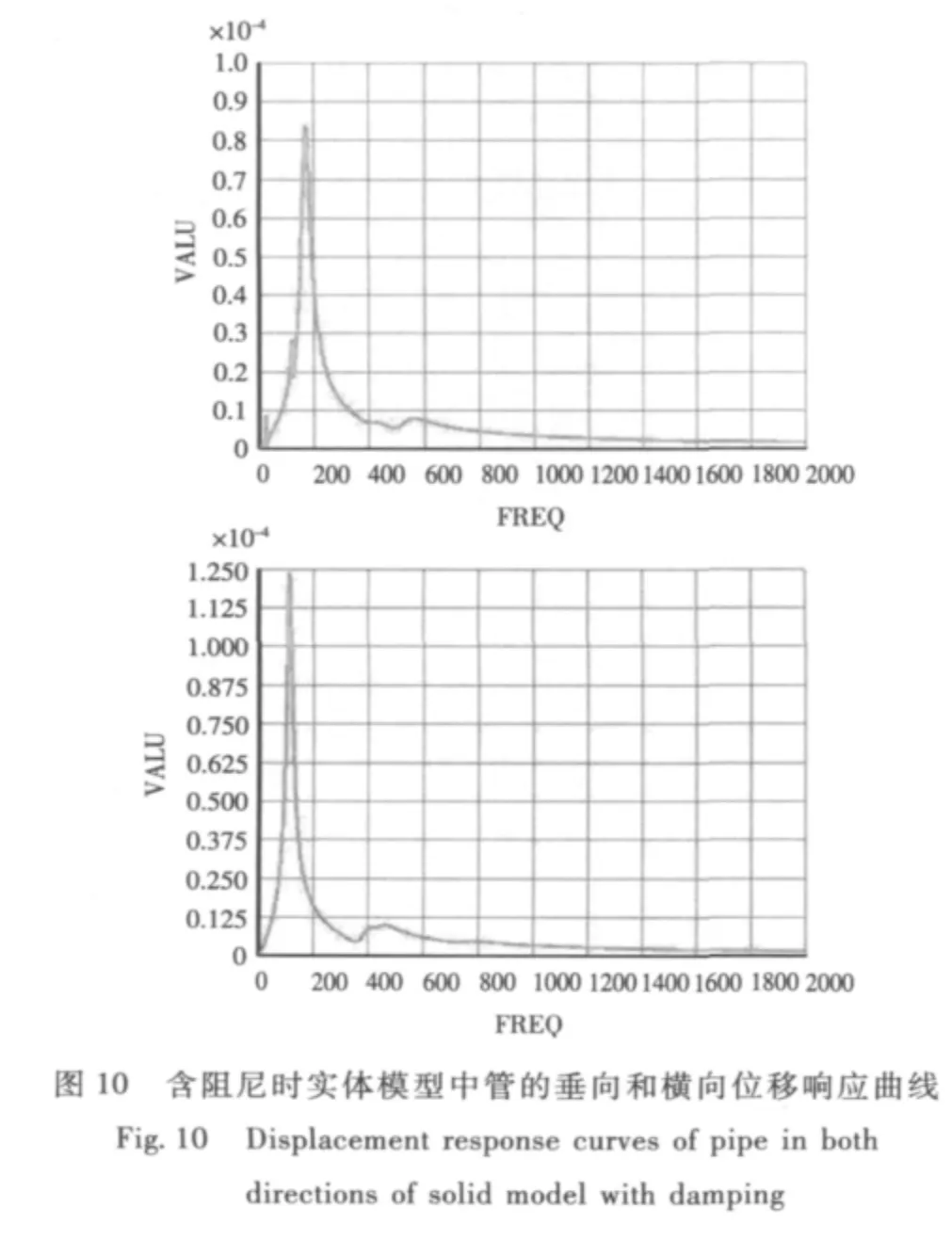
在相同條件下得到管路支架實體模型中管道的響應曲線如圖10所示。

圖9與圖10相比，2種情況下曲線共振峰的位置和峰值大小幾乎是一樣的。因此，從這一點可以看出，簡化模型在設置合適阻尼的情況下是能比較準確地模擬管道位移響應的。

4 結語

本文通過對管路支架實體模型進行含預應力的諧響應分析，了解支架的頻域特性，并在此基礎上建立了垂向和橫向2個方向的二自由度簡化模型。這種簡化模型不同于以往單自由度模型，它充分考慮了管路支架本身質量對其動力學特性的影響。經過驗算，這種簡化模型在設置合適的阻尼情況下能很好地模擬管路支架在頻域內的力學行為。另外要指出的是，這種模型沒有考慮管路支架在多個方向存在耦合的特性，這雖然會對分析的結果帶來一定的改變，但對整體結論的影響很小。因此，用這樣的簡化模型模擬管路支架在管路系統中動力學行為是合適的，這將在保證精度的基礎上大大簡化對管路系統的振動研究。

［1］師漢民，諶剛，吳雅.機械振動系統―分析……測試·建模·對策［M］.武漢:華中理工大學出版社，1992.

［2］陳精一，蔡國忠.電腦輔助工程分析ANSYS使用指南［M］.中國鐵道出版社，2001.

［3］JANSSON G，ZENG Ling-fu.On modeling piping supports in dynamic analysis of nuclear-power piping system［C］.Proceedingsofthe 16th InternationalConference on Nuclear Engineering，2008.

［4］蔣學武，朱石堅.船舶管道橡膠減振器的應用［J］.海軍工程大學學報，2000，(4):90 －91.JIANG Xue-wu，ZHU Shi-jian.The application of pipe rubber vibration isolators on warships［J］.Journal of Naval University of Engineering，2000，(4):90 －91.