某三缸發動機懸置的優化設計

韓全友，廖 武，李玉發，趙吉剛，彭宜愛

（安徽江淮汽車股份有限公司技術中心，合肥 236001）

為響應低碳低排放的要求，小排量發動機近年來得到廣泛應用，其中選擇三缸小排量發動機是當前汽車行業的一個趨勢。發動機是汽車上的一個主要振源，其振動由發動機經懸置系統傳遞到車架或車身上，尤其是三缸發動機，因為其自身的慣性力不平衡，給懸置的設計帶來了更大的困難。因此，發動機懸置系統參數的設計，對于汽車整車的減振降噪來說非常重要。對于發動機懸置系統，一方面為了限制發動機運動，要求懸置系統具有較高的剛度；另一方面為了使發動機產生的振動盡可能小地傳遞到車身，希望懸置要足夠軟。所以，在懸置系統參數設計時，要兼顧這兩個方面達到一致的最優解[1]。

1 優化方法

1.1 理論基礎

鑒于內燃機動力總成所受激勵及其作用方向的上述特點[2]，最大限度地解除動力總成一懸置系統的多自由度振動耦合，是使其具有良好隔振性能的基本方法，尤其是解除其懸置系統的側傾自由度、垂向自由度與其他自由度之間的彈性耦合，是懸置系統設計的關鍵。

對于一個多缸的發動機，發動機不平衡的擾動取決于氣缸的數目和布置形式。從表1可以看出，汽車上常用的幾種發動機中，三缸和四缸機沒有得到完全平衡。因此，對于使用這兩種機型的汽車，必須特別重視懸置系統的設計。

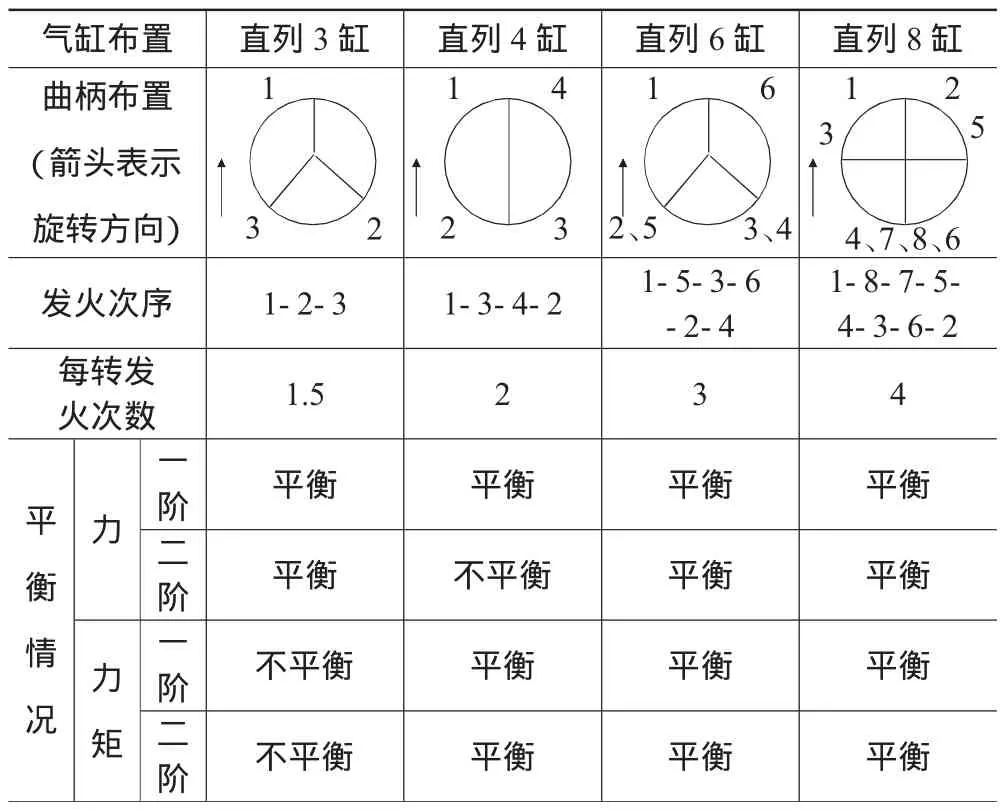
表1 四沖程往復式內燃機固有平衡特性表

對于發動機懸置系統參數進行優化，可以從不同角度提出目標函數和約束條件來建立不同的數學模型。常見的目標函數有：發動機懸置系統六自由度解耦和部分解耦；系統固有頻率的合理配置；系統的振動力傳遞率或支承處動反力最小[3-5]。

根據振動理論，懸置系統的隔振設計主要從系統的固有頻率考慮，當系統的固有頻率和相應的擾動頻率相同時，振動系統將發生共振，相應幅值大大增加。對發動機而言，低頻范圍內，其主要擾動力為繞曲軸方向的轉矩。當此擾動頻率和繞曲軸旋轉方向RY的固有頻率重合時，系統發生共振。通常使RY方向的固有頻率小于發動機正常工作時擾動頻率的0.707倍。同時，從整車各子系統的動力特性合理分配考慮，懸置系統的固有頻率還應避開其它子系統相應的振動頻率，如懸架、車身及車輪的振動頻率，以防由此引起發動機和其它子系統間的共振。此外，還要使懸置系統主要方向的振動得到解耦，至少也應該使它們的耦合程度得到降低。所以，無論從發動機懸置系統，還是汽車其它子系統的動力特性合理分配考慮，對發動機懸置系統的設計都必須從解耦和固有頻率的合理設計入手[6-9]。

1.2 建立目標函數

根據發動機懸置系統優化設計的要求，將固有頻率、解耦性用數學模型表示。通常對Z方向及RY方向的固有頻率和解耦性有較高要求，而其它振型的固有頻率只要控制在一定的范圍內即可，于是建立如下目標函數：

式中：x為設計變量；f0（z）、f0（RY）為設計要求的固有頻率值；f（z）、f（RY）為懸置系統的實際頻率值；dig為解耦性（100%，完全解耦）；W1、W2、W3、W4為加權系數。

1.3 能量解耦法

對動力總成懸置進行優化，常采用能量法進行解耦設計。能量分布矩陣是動力總成在做各階主振動時的能量分布，寫成矩陣形式，記作KE[10-11]。當動力總成以第k階固有頻率振動時，第i個廣義坐標分配到的能量（KEi）k為

式中：mij為動力總成質量矩陣中位于第i行、第j列的元素；（φk）i、（φk）j為第 k 階振型中第 i、j個元素；ωk為第k 階振動的固有頻率(i，j，k=1，2，……，6)。由此可得,以第k階固有頻率振動時，第i個廣義坐標所分配到的能量在總能量中的百分比：

式中：（KE）k為懸置系統的總能量；digik表示懸置系統在i方向的解耦程度，digik越大，解耦程度越高。

2 參數及設計變量優化

該車型采用橫置直列三缸汽油發動機，三點橡膠懸置，其中后懸置為抗扭拉桿式，系統布置如圖1所示；動力總成轉動慣量和慣性積見表2；懸置的位置和剛度參數見表3。

表2 動力總成參數

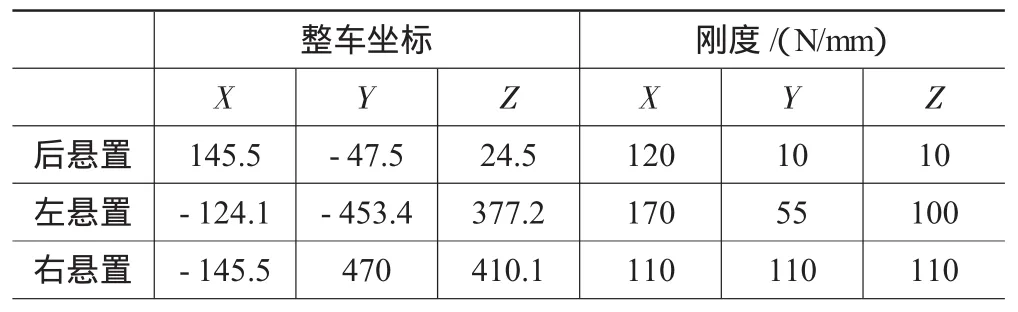
表3 優化前位置及剛度

由振動理論可知，剛度矩陣與以下因素有關：動力總成懸置的個數、各懸置的安裝位置、各懸置的彈性主軸與廣義坐標系之間的角度、各懸置在彈性主軸方向的剛度。其中調整懸置的位置對剛度矩陣及系統的解耦率影響最大，收效也最明顯，但考慮到該車型發動機艙及底盤的方案均已凍結，調整懸置位置將引起較大的設計變更，成本太高，故決定選擇懸置剛度為設計變量。

由前面分析可知，當動力總成繞曲軸的固有頻率小于發動機怠速激勵頻率的0.707倍時，才能達到隔振效果。本例中三缸發動機的怠速轉速為850 r/min，由式（4）得發動機的激勵頻率為21.25 Hz。因此，繞曲軸方向（RY）的固有頻率必須小于15 Hz。

式中：n為發動機轉速；i為發動機缸數；τ為發動機沖程。

由式（2）、式（3）可得優化前動力總成系統各階模態和能量分布情況，見表4。可見，X方向和RY方向固有頻率過于接近，且繞Z軸旋轉的固有頻率RZ=21.7與發動機怠速的激振頻率也過于接近，振動存在耦合，六自由度解耦程度不夠，是導致整車振動的主要原因。

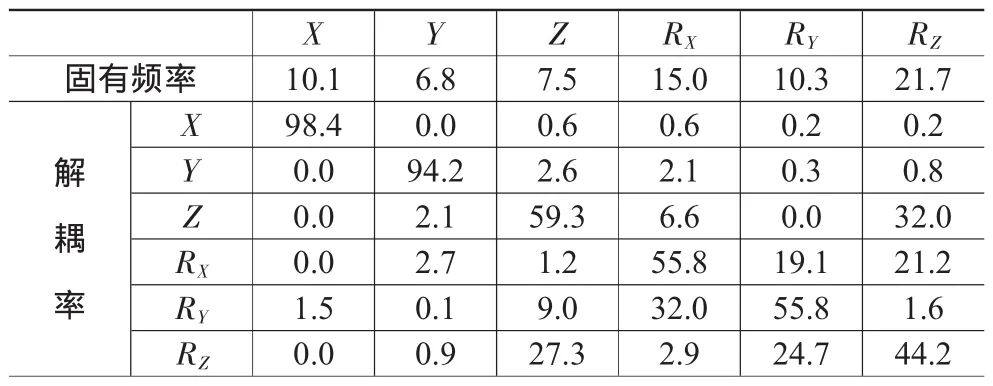
表4 優化前能量分布

結合原懸置系統懸置參數進行優化計算，計算中取加權系數：W1=3，W2=3，W3=2，W4=2。優化計算后懸置剛度及動力總成懸置系統的固有特性見表5、表6。從表5看出，優化后的右懸置的剛度比之前變化不大，左懸置的X方向剛度值降低較大。表6表明，動力總成懸置系統RZ方向的固有頻率由原來的21.7變為18.2，與激振頻率錯開；X方向和RY方向的固有頻率也間隔了1 Hz；各方向解耦率都在80%以上，滿足解耦要求。

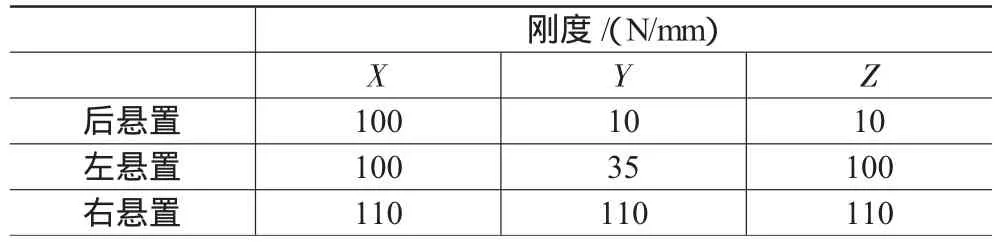
表5 優化后剛度

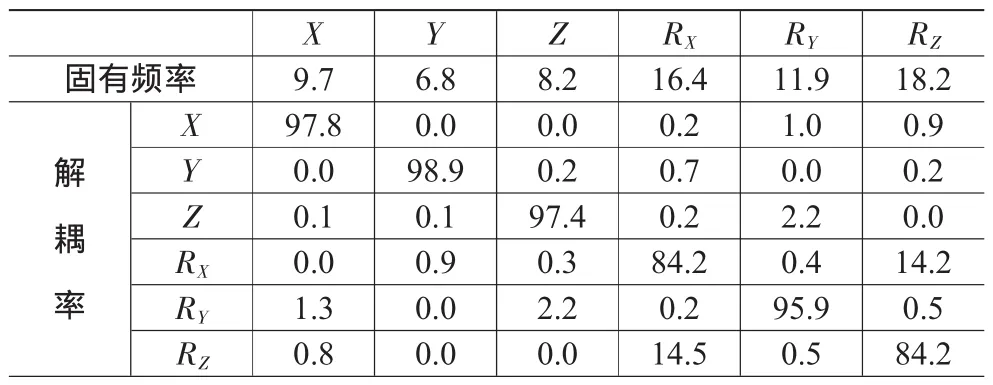
表6 優化后能量分布

為了驗證懸置優化后的隔振效果，對原車懸置系統優化前后進行了整車振動試驗。通過試驗得到，各測試點的振動傳遞率柱狀對比圖、車廂地板及方向盤的振動加速度有效均方根（RMS）值如圖2、圖3所示。從車廂地板振動能量的測試數據來看，懸置優化后，整車怠速的振動狀況得到了較好的改善，振動加速度RMS值在汽車低速及中速行駛時，均低于改進前。

3 結束語

發動機懸置系統設計是一個比較復雜的問題，涉及的因素較多，其設計的優劣對整車的振動特性會產生重要的影響。理想的發動機懸置應能隔離發動機在轉速范圍內引起的擾動，并能防止路面激勵引起的振動。本文對該車懸置系統剛度參數進行了優化計算及改進設計，并通過整車振動試驗證實了理論計算的正確性，用最少的變動、最低的成本使該匹配三缸發動機的車型的振動情況得到了改善。

[1]龐劍，諶剛，何華.汽車噪聲與振動—理論與應用[M].北京：北京理工大學出版社，2006.

[2]周龍保.內燃機學[M].北京:機械工業出版社，1999.

[3]呂振華，范讓林.動力總成－懸置系統振動解耦設計方法[J].機械工程學報，2005，41（4）

[4]黃信，柏世川，章竹一.汽車發動機懸置系統設計[J].合肥工業大學學報：自然科學版，2009，（S1）

[5]徐石安.汽車發動機彈性支承隔振的解耦方法[J].汽車工程，1995，（4）：198-204.

[6]侯勇，趙濤.動力總成懸置系統解耦設計[J].汽車工程，2007，12.

[7]周志革，武一民，崔根群，等.發動機懸置系統參數的優化設計[J].機械設計，2003，20（3）：53-55.

[8]范讓林，呂振華.剛體－彈性支承系統振動解耦評價方法分析[J].工程力學，2006，23（7）

[9]Seonho Cho.Configuration and Sizing Design Optimization of Power train Mounting Systems[J].Intenrational Jounral of Vehicle Design，2000，24（1）

[10]王天利，孫營，田永義.基于能量法解耦的汽車動力總成懸置系統優化[J].機械設計與制造，2006，（7）：31-33.

[11]周密，侯之超.基于遺傳算法的動力總成懸置系統優化設計[J].汽車技術，2006，（9）：13-16.