描述邏輯FLε合一算法

劉 凱

（遼寧師范大學(xué)數(shù)學(xué)學(xué)院 遼寧 大連 116029）

0 引言

描述邏輯是一種基于對(duì)象的知識(shí)表示的形式化，也叫概念表示語言或術(shù)語邏輯，一個(gè)描述邏輯系統(tǒng)包含四個(gè)基本組成部分：表示概念和關(guān)系的構(gòu)造集；TBox包含斷言；ABox實(shí)例斷言；TBox和ABox上的推理機(jī)制。它們能夠被用作表示在結(jié)構(gòu)上和形式上為人所熟知的方法的應(yīng)有領(lǐng)域中的概念知識(shí)。它們應(yīng)用于各種各樣的應(yīng)用領(lǐng)域，例如：自然語言，組態(tài)，數(shù)據(jù)庫和本體[1]。

兩個(gè)項(xiàng)?child.Rich∩?child.Woman和?child.（Rich∩Woman）是相等的，如果我們用存在限制符（?r.C）取代值限算子符，那么這個(gè)等式不再成立。然而，?child.Rich∩?child.（Woman∩Rich）≡?child.（Woman∩Rich）通過用項(xiàng) Female∩Human取代 Woman，這個(gè)概念項(xiàng)Woman∩?child.Woman 和 Female∩Human∩?child.（Female∩Human）是不相等的，但是它們意味著表示相同的概念。這兩個(gè)項(xiàng)明顯地能通過概念項(xiàng)Female∩Human替代第一個(gè)項(xiàng)中的概念名Woman而被做成相等。這導(dǎo)出我們的概念項(xiàng)的合一算法，也就是，兩個(gè)概念項(xiàng)通過應(yīng)用一個(gè)適當(dāng)?shù)奶娲渲刑娲ㄟ^概念項(xiàng)取代概念名。

1 FLε的合一算法

首先我們定義FLε-概念項(xiàng)及這些項(xiàng)的包含和相等關(guān)系的語法和語義。FLε的用通常的方法來定義，應(yīng)用一個(gè)解釋I=（DI，·I）的概念，且存在一個(gè)非空領(lǐng)域DI和一個(gè)解釋函數(shù)·I能夠分配關(guān)于的二元關(guān)系到角色名及DI的子集到概念項(xiàng)。正如表1的列所表示的語義。

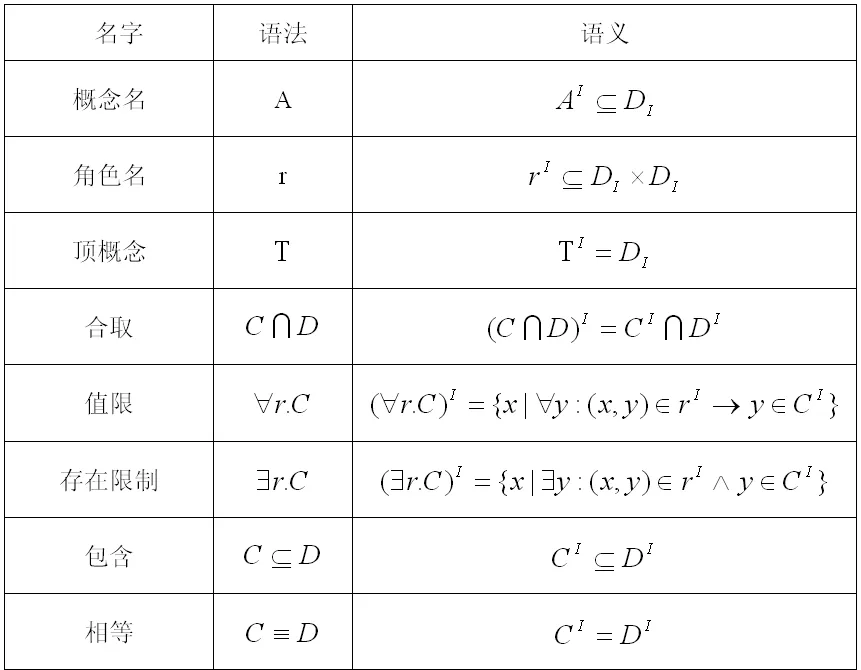
表1 FLε的語法和語義Tab.1 Syntax and Semantics of FLε

為了定義概念項(xiàng)的合一算法，我們首先引入關(guān)于概念項(xiàng)的一個(gè)替代操作概念。為了這個(gè)目的，我們劃分概念名集到一個(gè)概念變量集Nv（它可能被替代所取代）和概念常量集Nc（它一定不能被替代所取代）。一個(gè)替代σ是一個(gè)從Nv到FLε-概念項(xiàng)集的映射，這個(gè)映射在明顯的方式下被擴(kuò)展到概念項(xiàng)，也就是，-σ（A）:=A，對(duì)所有的 A∈Nc，σ（T）:=T，σ（C∩D）:=σ（C）∩σ（D），σ（?r.C）：＝?r.σ（C），且 σ（?r.C）：＝?r.σ（C）。

定義 1 一個(gè) FLε-合一算法問題是形如 Γ＝｛C1≡？D1，…，Cn≡？Dn｝，其中 C1，D1，…，Cn，Dn是 FLε-概念項(xiàng)，這個(gè)替代 σ 是 Γ 中一個(gè)合一算子（或者解），當(dāng)且僅當(dāng) σ（Ci）≡σ（Di）其中 i=1，…，n，這個(gè)例子中，Γ 被叫做可解的或可合一的。

通常情況下，合一算子能用實(shí)例前序≤·來比較。令Γ是一個(gè)FLε-合一算法問題，V是出現(xiàn)在Γ中的變量集，σ，θ是這個(gè)問題的兩個(gè)合一算子。我們定義σ≤·θ當(dāng)且僅當(dāng)有一個(gè)替代λ，對(duì)于所有的X∈V使得 θ（X）=λ（σ（X））。

如果σ≤·θ，那么我們說θ是σ的一個(gè)例子。

定義2 令Γ是一個(gè)FLε-合一算法問題，替代集M被叫做Γ的一個(gè)完備合一算子集當(dāng)且僅當(dāng)它滿足接下來的兩個(gè)性質(zhì)：

1.M的每一個(gè)元素是Γ的一個(gè)合一算子；

2.如果θ是Γ的一個(gè)合一算子，那么存在一個(gè)合一算子σ∈M，使得σ≤·θ。這個(gè)集合M被叫做Γ的一個(gè)最小合一算子集，當(dāng)且僅當(dāng)它額外地滿足

3.如果 σ，θ∈M，那么 σ≤·θ蘊(yùn)含 σ＝θ。

定義3 令Γ是一個(gè)FLε-合一算法問題。這個(gè)問題有單一的類型（有限的，無限的）當(dāng)且僅當(dāng)它有一個(gè)最小完備合一算子集基數(shù)1（有限基數(shù)，無限基數(shù)）。如果Γ沒有一個(gè)最小完備合一算子集，那么它是零型。

2 FLε的相等和包含

為了能夠特征化FLε-概念項(xiàng)的相等，一個(gè)簡(jiǎn)化的FLε-概念項(xiàng)在[17]被引入，一個(gè)給定的FLε-概念項(xiàng)能通過應(yīng)用合取的交換和結(jié)合模態(tài)的如下規(guī)則轉(zhuǎn)化成一個(gè)相等的簡(jiǎn)化項(xiàng)。C∩T→C，A∩A→A?r.C∩?r.D→?r.C 對(duì)所有的 FLε-概念項(xiàng) C，D 且 C?D

定理1 令C，D是FLε-概念項(xiàng)，且C?，D?是C和D各自簡(jiǎn)化形式。那么C≡D當(dāng)且僅當(dāng)由∩的結(jié)合和交換決定的C?恒等于D?。

引理1 如果 C，D是FLε-概念項(xiàng)的簡(jiǎn)化，使得?r.D?C，那么C要么是 T，要么是 C=?r1.C1∩…∩?r.Cn的形式，其中 n≥1；C1，…，Cn是簡(jiǎn)化的并且關(guān)于包含是成對(duì)不可比較的，而且D?C1，…，D?Cn。相反的，如果 C，D 是 FLε-概念項(xiàng)使得 C=?r.C1∩…∩?r.Cn且 D?C1，…，D?Cn，那么?r.D?C。 FLε-合一算法的可判定的證明中，我們將利用這個(gè)事實(shí)嚴(yán)格包含的你順序是有充分根據(jù)的。

命題1 沒有 FLε-概念項(xiàng)的極大結(jié)果 C0，C1，C2，C3，…使得 C0?C1?C2?C3?…。

3 一個(gè)零型的FLε-合一算法問題

為了證明FLε有合一算法零型，我們展示一個(gè)FLε-合一算法問題有這種類型。

定理2 令 X，Y是變量， 這個(gè) FLε-合一算法問題 Γ:＝｛X∩?r.Y≡？?r.Y｝有合一算法零型。

4 可判定性問題

在我們能描述關(guān)于FLε-合一算法的可判定程序之前，我們必須引入一些概念。一個(gè)FLε-概念項(xiàng)被叫做一個(gè)原子當(dāng)且僅當(dāng)它是概念名（也即是，概念常量或者概念變量），一個(gè)值限?r.D或者一個(gè)存在限制?r.D。明顯地，任何FLε-概念項(xiàng)是（等于）原子項(xiàng)的一個(gè)合取，其中空合取是T。一個(gè)FLε-概念項(xiàng)C的原子集At（C）推導(dǎo)的定義：如果C=T，那么 At（C）:=φ；如果 C 是一個(gè)概念名，那么 At（C）:=｛C｝；如果 C=?r.D 那么 At（C）:=｛C｝∪At（D）；如果 C=C1∩C2，那么 At（C）:=At（C1）∪At（C2）。

概念名、值限?r.D和存在限制?r.D其中D是一個(gè)概念名或者T被叫做平坦的原子。這個(gè)FLε-合一問題Γ是平坦的當(dāng)且僅當(dāng)它僅僅包括接下來的形式的方程：-X≡？C其中X是一個(gè)變量而C是是非變量的平坦的原子；

-X1∩…∩Xm≡？Y1∩…∩Yn其中 X1，…，Xm，Y1，…，Yn是變量。

引理 2.令 C，D，D′是 FLε-概念項(xiàng)使得 D＞isD′而且 C 是簡(jiǎn)化的，并且含有至少一個(gè)D的出現(xiàn)，如果C′通過用D′取代所有D的出現(xiàn)從C 中獲得，那么 C＞isC′。

命題2 令Γ是一個(gè)FLε-合一問題。那么Γ是可解的當(dāng)且僅當(dāng)它有一個(gè)最小的簡(jiǎn)化的基合一算子。

引理3 令Γ是一個(gè)FLε-合一問題，且γ是一個(gè)最小的簡(jiǎn)化基算子。如果C是γ的 一個(gè)原子，那么有Γ的一個(gè)非變量原子D，使得C≡γ（D）。

命題3 令Γ是一個(gè)平坦的FLε-合一問題且γ是Γ的一個(gè)最小的簡(jiǎn)化基算子。如果X是出現(xiàn)在Γ中的一個(gè)概念變量，那么γ（X）≡T或者有一個(gè) Γ 的非變量原子 D1，…，Dn（n≥1）使得 γ（X）≡γ（D1）∩…∩γ（Dn）。

定理3 εL-合一算法是非決定性多項(xiàng)式完全（NP-Complete）

5 結(jié)論

本文分析了描述邏輯合一算法的研究進(jìn)展和存在問題，在Badder F的基礎(chǔ)上又進(jìn)一步研究了帶存在和任意算子的描述邏輯FLε的合一算法問題。給出了FLε的合一算法的定義，我們已經(jīng)證明在DLFLε的合一算法是零型和其中的εL-合一算法是非決定性多項(xiàng)式完全（NP-complete）。

模態(tài)邏輯和描述邏輯有一個(gè)緊密的聯(lián)系是眾所周知的。例如這個(gè)DLALC，它能向FLε加入否定來獲得，對(duì)應(yīng)于基本的（多）模態(tài)邏輯K，在K中的合一算法的判定是一個(gè)長(zhǎng)期存在的開問題。最近，在K-一些擴(kuò)展（例如，通過一元模態(tài)）的合一算法不可判定已經(jīng)被證明，子布爾模態(tài)邏輯的合一算法（也即是，模態(tài)邏輯在所有布爾操作符下不閉，正如FLε的模態(tài)邏輯相等），據(jù)我們所知，模態(tài)知識(shí)中沒有被考慮。

［1］Baader,F.,Kusters,R.:Matching in description logics with existential restrictions[Z].In:Proc.KR 2000,2000.

［2］Baader,F.,Narendran,P.Unification of concepts terms in description logics[J].J.of Symbolic Computation 31(3),2001.

［3］Badder F,Unification in Commutative Theories[J].J.of Symbolic computation,1989,8(5).

［4］Badder F,Morawska.Unification in the Description logic εL[Z].