基于TailVaR的我國保險公司經(jīng)濟資本度量研究

王 穩(wěn)，郭 祥

(對外經(jīng)濟貿(mào)易大學(xué)保險學(xué)院，北京100029)

一、問題提出

經(jīng)濟資本概念出現(xiàn)于上世紀70年代，美國信孚銀行首次將風(fēng)險因素納入自身經(jīng)營業(yè)績的考察過程，提出基于風(fēng)險調(diào)整的收益率指標［1］。隨著風(fēng)險量化模型的不斷發(fā)展，經(jīng)濟資本在企業(yè)風(fēng)險管理中的應(yīng)用日趨深入。保險公司是專門經(jīng)營風(fēng)險的企業(yè)，經(jīng)濟資本對于企業(yè)的產(chǎn)品定價、績效考核、業(yè)務(wù)創(chuàng)新乃至戰(zhàn)略制定都具有重要作用［2］。經(jīng)濟資本需求量與保險公司面臨的風(fēng)險水平正相關(guān)。一定置信水平上的經(jīng)濟資本數(shù)量全面客觀地反映了保險公司的整體風(fēng)險。如何準確確定經(jīng)濟資本量是保險公司風(fēng)險管理研究的核心問題。目前理論界和實務(wù)界有許多關(guān)于經(jīng)濟資本度量的方法，諸如VaR、違約損失率等，但多數(shù)不滿足風(fēng)險度量一致性原則，并且在風(fēng)險損失分布擬合時多采用正態(tài)分布，未考慮風(fēng)險損失分布的厚尾特征。本文尋求滿足風(fēng)險度量一致性條件下非正態(tài)分布的經(jīng)濟資本度量方法，借鑒Harry Panjer(2002)提出的TailVaR方法對我國保險公司的經(jīng)濟資本進行測算［3］，試圖為投保者、監(jiān)管機構(gòu)與保險公司經(jīng)營者決策提供參考。

全文內(nèi)容安排如下:首先提出研究問題，明確全文的研究方向。第二部分從經(jīng)濟資本度量思路、經(jīng)濟資本度量模型與風(fēng)險度量一致性三個方面對國內(nèi)外的相關(guān)文獻進行梳理。第三部分介紹TailVaR的經(jīng)濟資本度量方法基本內(nèi)容、優(yōu)勢及其對極端風(fēng)險損失的處理。第四部分通過我國保險公司數(shù)據(jù)的實證分析對TailVaR方法的適用性加以驗證。最后部分為研究結(jié)論。

二、研究綜述

經(jīng)濟資本度量本質(zhì)上依賴于風(fēng)險度量過程，關(guān)于經(jīng)濟資本度量思路方面的研究文獻主要集中在兩個方面:一是通過各個業(yè)務(wù)線的風(fēng)險匯總測算整體風(fēng)險，主要選用Copula函數(shù)對多風(fēng)險聯(lián)合分布的經(jīng)驗?zāi)M，是一種自下而上的風(fēng)險度量方法;二是拋棄著重于一種或幾種風(fēng)險的評估方法，自上而下測算企業(yè)整體應(yīng)承擔(dān)的風(fēng)險［4］，主要采用 VaR、TailVaR 等方法。

文獻關(guān)于經(jīng)濟資本的度量模型研究主要集中在三個方面:統(tǒng)計度量模型、偏離校準模型與過程模擬模型。其中，經(jīng)濟資本度量以統(tǒng)計度量模型最為普遍，統(tǒng)計度量模型借助于預(yù)先分類的風(fēng)險，依據(jù)歷史損失數(shù)據(jù)估算出風(fēng)險損失的概率分布，以達到計算經(jīng)濟資本的目的，主要包括內(nèi)部衡量法、VaR法、極值法等。Michael K.Ong(1999)提出的信用風(fēng)險經(jīng)濟資本數(shù)量模型，強調(diào)風(fēng)險損失受到違約概率、違約風(fēng)險暴露、違約損失率等因素的影響［5］。KMV公司1993年提出基于期權(quán)定價理論的Credit Monitor模型，J.P.Morgan于1997年推出Credit Metrics模型，瑞士信貸1997年提出Credit Risk+模型，麥肯錫1998年提出Credit Porfolio View模型，上述模型對市場信用風(fēng)險導(dǎo)致的損失分布進行分析，并在國際銀行業(yè)得到廣泛使用［6］。此外，還存在基于交易對手的經(jīng)濟資本分析，利用風(fēng)險暴露的差異計算交易對手風(fēng)險的經(jīng)濟資本［7］。借助于VaR對經(jīng)濟資本度量，即在一定持有期與置信區(qū)間內(nèi)，企業(yè)的最大潛在損失，扣除預(yù)期損失后得出經(jīng)濟資本，是目前經(jīng)濟資本度量最常用的方法。研究成果主要針對如何取得VaR展開，如使用方差——協(xié)方差法、參數(shù)法、歷史數(shù)據(jù)模擬法、蒙特卡羅模擬法、極值方法等。Jorion(1997)認為VaR描述了市場的正常波動，大于VaR值的損失只會以小概率發(fā)生［8］。由于通常假定資產(chǎn)收益率服從正態(tài)分布，并且不能解釋資金的時間價值與風(fēng)險溢價［9］，不依賴于正態(tài)性假定的擴展模型如市場風(fēng)險的粒度調(diào)整方法、基于半漸進方法的單因素市場風(fēng)險模型成為新的研究方向［10-11］。在組合風(fēng)險方面，多選取貝塔分布、逆高斯分布與廣義帕累托分布對多風(fēng)險的經(jīng)濟資本進行度量，其中基于廣義帕累托分布的測算結(jié)果最符合實際情況［5］，Vasicek分布表明了組合損失分布收斂于極限形式的可能情況，在計算組合風(fēng)險時能夠表現(xiàn)出信用風(fēng)險的左偏性質(zhì)，也具有相應(yīng)的 優(yōu) 越 性［12］。Jacobson，Jesper Lindé，Kasper Roszbach(2005)使用模特卡羅對資產(chǎn)組合損失分布模擬并計算出經(jīng)濟資本數(shù)額［13］。Bandyopadhyay(2008)通過計算股票市值計算違約距離的方法得出商業(yè)銀行所需的經(jīng)濟資本總量［14］。在計算組合風(fēng)險經(jīng)濟資本時出現(xiàn)的Copula函數(shù)及其應(yīng)用應(yīng)得到足夠重視，該方法借助樣本數(shù)據(jù)與風(fēng)險資產(chǎn)收益率邊緣分布得出風(fēng)險損失聯(lián)合分布，克服了線性相關(guān)系數(shù)與秩相關(guān)系數(shù)的不足［15-20］。

偏離校準模型主要分析風(fēng)險不同的波動幅度對經(jīng)濟資本變動的影響，主要包括情景分析、壓力測試等。其中，情景分析與壓力測試作為診斷工具檢驗各類別投資組合的經(jīng)濟資本是否充足以及相應(yīng)的資本配置的限制是否合理，對金融機構(gòu)經(jīng)濟資本配置和風(fēng)險暴露修正做出了積極貢獻［22-23］，Embrechts(1999)［24］，Moneil(1999)［25］推導(dǎo)出基于極值理論(Extreme Value Theory，EVT)與壓力情景下資產(chǎn)組合損失及其發(fā)生概率的計算方法。過程模擬模型關(guān)注風(fēng)險之間的相關(guān)性，更加真實地模擬風(fēng)險損失分布，包括因素分析法與貝葉斯法。Kiihn提出反映突發(fā)性操作風(fēng)險的度量模型，或通過貝葉斯方法建立因果推斷模型對風(fēng)險進行描述［26-27］。Basel委員會提出基本指標法、標準法與高級法三種方法對損失分布進行估計。Alexander(2000)將貝葉斯方法用于操作風(fēng)險度量，有效結(jié)合風(fēng)險管理控制與度量，利用主觀先驗信息進行情景分析［27］。King(2001)建立 Delta-EVT模型，使用Delta因子度量高頻低損的操作風(fēng)險損失［28］。Marcelo(2002)說明貝葉斯網(wǎng)絡(luò)在商業(yè)銀行風(fēng)險管理中的應(yīng)用［29］。Hubner(2005)建立Oprisk+模型，檢驗不同分布的擬合情況［30］，但總體上該類模型的應(yīng)用范圍仍然較窄，有待于進一步擴展。

表1 各種風(fēng)險度量方法的一致性判斷

現(xiàn)階段諸如標準差與VaR等傳統(tǒng)風(fēng)險度量方法多被用來研究經(jīng)濟資本分配問題以及金融資產(chǎn)損失分布下的條件風(fēng)險價值［31-32］，但是上述度量方法都沒有體現(xiàn)出Markowitz資產(chǎn)組合理論的風(fēng)險分散化效應(yīng)，且都不滿足風(fēng)險的次可加性(Glenn Meyers，2000)。各種風(fēng)險度量方法的一致性判斷見表1。隨著風(fēng)險度量一致性原則的提出［33］，多種新型的風(fēng)險度量方法陸續(xù)出現(xiàn)，Artzner P(1999)針對VaR的不足，提出滿足風(fēng)險度量一致性原則的風(fēng)險度量函數(shù) TailVaR，Landsman＆Valdez(2003)、Denault D(2005)、Furman＆Landsman(2005)、Vernic(2006)、Vanduffel(2008)則在 Artzner P的基礎(chǔ)上探討了經(jīng)濟資本在實際運用層面的合理應(yīng)用［18，34-35，37］。Harry Panjer(2002)在 Edwatd Zaik.James.Artzner P等人的研究基礎(chǔ)上，利用符合一致性原則的風(fēng)險度量函數(shù)TailVaR分析了保險公司的風(fēng)險狀況，并為保險公司的經(jīng)濟資本度量提供了新的思路［3］。

國內(nèi)經(jīng)濟資本度量理論方面，多位學(xué)者對VaR的理論發(fā)展進行介紹并對其在我國的實用性進行探討。非參數(shù)統(tǒng)計方法在VaR中得到了廣泛應(yīng)用［38］。基于馬爾科夫鏈模特卡羅模擬計算VaR，有效克服了傳統(tǒng)方法靜態(tài)性的缺陷［39］。基于廣義誤差分布的VaR算法與改進的bootstrap算法成為近期VaR計算的新發(fā)展［40-41］。

經(jīng)濟資本度量應(yīng)用方面文獻很多，一是基于清償能力的角度從靜態(tài)與動態(tài)兩個方面研究經(jīng)濟資本與VaR的關(guān)系，并通過經(jīng)濟資本度量的對比分析發(fā)現(xiàn)各種方法的不足之處，為我國金融機構(gòu)提供借鑒［42-43］;二是比較總體經(jīng)濟資本的測度方法，重點針對經(jīng)濟資本加總方法進行研究［44］，并針對時間序列采用GARCH與Copula模型度量經(jīng)濟資本［45-46］。

國內(nèi)對于TailVaR風(fēng)險度量方法的研究較少。梁凌、譚德俊、彭建剛(2005)討論了基于TailVaR函數(shù)的風(fēng)險度量與經(jīng)濟資本分配標準，并采用違約率均值不變條件下的Credit Risk+模型對我國商業(yè)銀行經(jīng)濟資本分配進行了實證分析［47］。滕帆(2005)在Harry Panjer(2002)的基礎(chǔ)上用TailVaR函數(shù)定量測算了我國五家保險公司的經(jīng)濟資本數(shù)量［48］。李博(2009)用風(fēng)險度量一致性原則及TailVaR函數(shù)定量估算了我國五家商業(yè)銀行的經(jīng)濟資本數(shù)量，并進行比較分析［49］。朱建平(2009)利用尾部風(fēng)險價值法對保險經(jīng)濟資本進行測量［50］。竇爾翔，熊燦彬(2011)計算我國商業(yè)銀行與保險公司基于TailVaR的經(jīng)濟資本，并以此為基礎(chǔ)計算出RORAC，對銀行與保險公司的經(jīng)營風(fēng)險與運作效率進行對比分析［51］。但是上述研究都基于投資收益率(損失率)正態(tài)分布的假定，沒有充分體現(xiàn)風(fēng)險損失的厚尾，導(dǎo)致實證過程中只能依靠提高置信水平來補償所造成的經(jīng)濟資本偏小估計。

此外，比較國內(nèi)外研究現(xiàn)狀可以發(fā)現(xiàn)，經(jīng)濟資本是企業(yè)風(fēng)險管理的核心工具，是資本風(fēng)險管理的重要內(nèi)容，然而相對于商業(yè)銀行，現(xiàn)有關(guān)于保險公司經(jīng)濟資本管理的理論研究和實證研究都非常缺乏，這對于我國保險公司實施企業(yè)風(fēng)險管理形成了極大的障礙。目前企業(yè)風(fēng)險管理視角下的風(fēng)險分析與經(jīng)濟資本度量面臨如何讓風(fēng)險一致性原則在實踐中得到有效運用的挑戰(zhàn)。

三、基于TailVaR的經(jīng)濟資本度量方法

(一)TailVaR度量方法及分布修正

經(jīng)濟資本度量本質(zhì)上是一種風(fēng)險度量應(yīng)用，是將保險企業(yè)的風(fēng)險損失這一隨機變量轉(zhuǎn)化成某一置信區(qū)間確定值的過程。傳統(tǒng)的風(fēng)險度量方法與風(fēng)險一致性度量方法存在差距。因此，Artzner(1999)提出基于TailVaR方法的一致性風(fēng)險度量方法。TailVaR函數(shù)(又稱為條件尾部期望)定義如下:

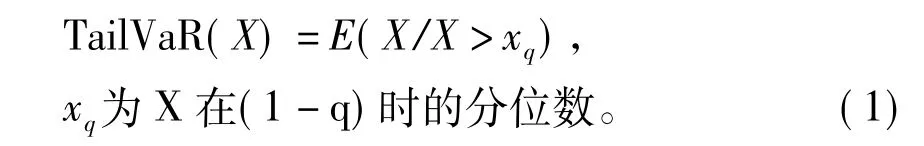
本文將保險公司的利潤(或凈損失)視為隨機變量，由此求得資本額的TailVaR就是為彌補風(fēng)險損失保險公司所應(yīng)準備的經(jīng)濟資本。目前研究多從參數(shù)法中的正態(tài)分布展開，并使用代數(shù)方法求解TailVaR。本文仍借鑒這一研究思路，在Harry Panjer、滕帆等人的分析框架基礎(chǔ)上通過修正損失率的厚尾分布形式，計算出不符合正態(tài)分布的TailVaR值，重新對我國保險公司的經(jīng)濟資本進行度量，以更好地符合現(xiàn)代保險公司的實際風(fēng)險狀況。

對于式(1)，對于分布函數(shù)已知的常規(guī)性分布可以依據(jù)代數(shù)方法推導(dǎo)出TailVaR的計算公式。現(xiàn)有的常規(guī)性分布函數(shù)包括正態(tài)分布、對數(shù)正態(tài)分布、T分布與Gamma分布，針對目前研究使用的損失分布形式，本文主要介紹正態(tài)分布和Gamma分布的TailVaR計算。

1.正態(tài)分布的TailVaR計算

均值為μ，標準差為σ的正態(tài)分布TailVaR計算公式為:

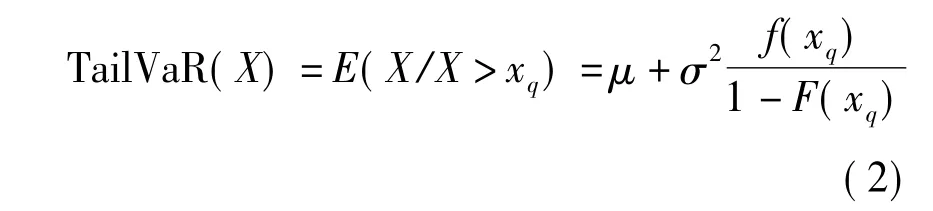
其中，f(x)為正態(tài)分布的概率密度函數(shù)，F(xiàn)(x)為正態(tài)分布的累積分布函數(shù)，xq為X在(1-q)時的分位數(shù)。由于任意正態(tài)分布都可以轉(zhuǎn)化為標準正態(tài)分布，對于損失率服從正態(tài)分布的保險公司Tail-VaR值可以借助于標準正態(tài)分布進行計算，計算公式如下:

其中，Y服從標準正態(tài)分布。不同破產(chǎn)概率下的標準正態(tài)分布的VaR與TailVaR值如表2所示，一般正態(tài)分布的 TailVaR值可以通過公式(3)計算得出。

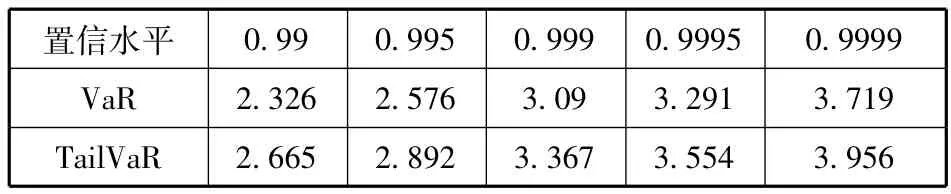
表2 標準正態(tài)分布各置信水平下的VaR與TailVaR計算

2.Gamma分布的TailVaR計算

對于非正態(tài)部分的TailVaR計算，不再具有正態(tài)分布的簡化計算，只能通過定義式計算，以Gamma分布為例，其TailVaR計算公式如下:

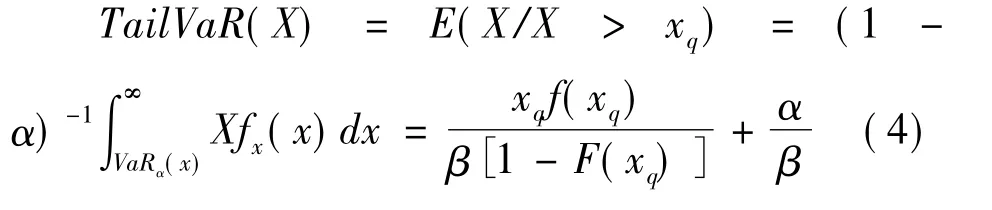
其中，f(xq)是Gamma分布的密度函數(shù)，F(xiàn)(x)為Gamma分布的累積分布函數(shù)。

對于其他損失分布的TailVaR計算與此類似，在此省略計算過程。包含上述損失分布的常用分布的TailVaR計算公式如表3所示。

表3 基于參數(shù)法的部分隨機分布TailVaR計算公式

3.非常規(guī)分布的TailVaR計算

對于非常規(guī)分布可以采用線性規(guī)劃方法進行求解［32］。通過引用業(yè)績函數(shù)，將TailVaR的度量轉(zhuǎn)化為業(yè)績函數(shù)最小化問題，利用線性凸規(guī)劃進行求解。令f(x，y)表示損失與不確定性的混合函數(shù)，x表示風(fēng)險頭寸，y表示風(fēng)險損失發(fā)生的參數(shù)，則置信度q內(nèi)的損失發(fā)生概率為Ω(x，q):

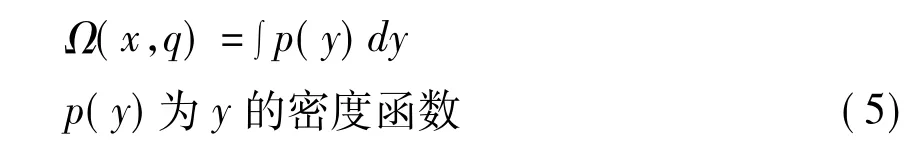
在風(fēng)險頭寸x不變的前提下，Ω(x，q)可以作為風(fēng)險損失分布函數(shù)。不失一般性假定該函數(shù)滿足對q處處連續(xù)，且是q的非減函數(shù)。對于任何α∈(0，1)，風(fēng)險損失的TailVaR定義為:

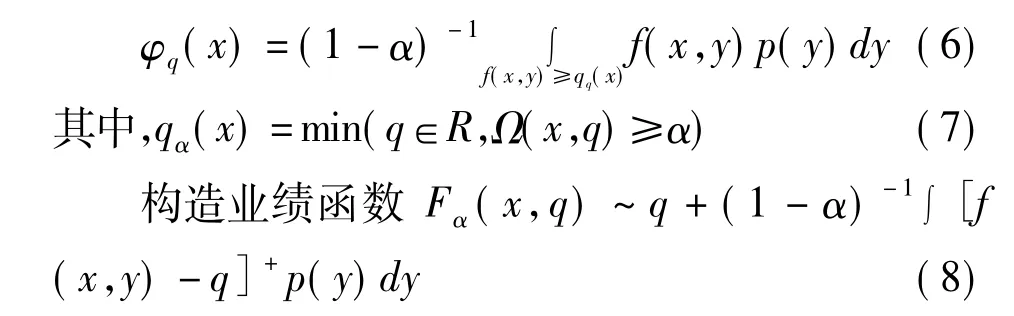
利用線性凸規(guī)劃可以對上述業(yè)績函數(shù)最小化進行求解，求得相應(yīng)的TailVaR值，具體步驟詳見Rockafeller與 Uryasev的論文［32］。另外，極值法在TailVaR計算方面的應(yīng)用是一種新興的研究方法，一般做法是針對超出置信度的數(shù)據(jù)首先使用更為合適的分布形式進行擬合以更有效地描述尾部特征，在此基礎(chǔ)上采用參數(shù)法計算該分布的TailVaR數(shù)值。

(二)TailVaR計算方法的優(yōu)點

TailVaR計算方法符合風(fēng)險度量一致性，滿足以下條件:

1. 次可加性：ρ(X+Y)≤ρ(X)+ρ(Y)。該條件說明聯(lián)合風(fēng)險損失小于單一風(fēng)險損失之和，只有各項風(fēng)險完全相關(guān)時，等號才能取得。而現(xiàn)實中保險公司面臨的各項風(fēng)險不是完全相關(guān)的，存在風(fēng)險的分散效應(yīng)。這是全面風(fēng)險管理理論的基本結(jié)論，通過公司內(nèi)部的風(fēng)險整合，可以對沖部分風(fēng)險，使得整體風(fēng)險小于各業(yè)務(wù)線風(fēng)險之和。Tail-VaR度量方法能夠反映出風(fēng)險分散效應(yīng)，更有效地反映企業(yè)整體層面的風(fēng)險。

2.單調(diào)性：若X≤Y成立，則 ρ(X)≤ρ(Y)成立。該條件表明TailVaR所涉及的風(fēng)險是通常意義上風(fēng)險，即風(fēng)險水平與風(fēng)險損失正相關(guān)，較大的風(fēng)險水平要求更多的經(jīng)濟資本覆蓋風(fēng)險損失。

3.正齊次性：對于任意正數(shù) λ，ρ(λX)=λρ(X)。風(fēng)險度量值是相對的，該條件可以去除風(fēng)險度量過程中的量綱影響，同時也表明資產(chǎn)組合一定的前提下，資產(chǎn)規(guī)模與資產(chǎn)風(fēng)險存在比例關(guān)系。

4.平移不變性：對于任意確定性損失η，ρ(X+η)=ρ(X)+η。該條件表明，增加確定性資產(chǎn)不會影響TailVaR度量的風(fēng)險價值，如果企業(yè)增加了確定性資產(chǎn)，則所需的經(jīng)濟資本會下降，下降的數(shù)額等于增加的確定性資產(chǎn)價值。

上述四個約束構(gòu)成風(fēng)險度量一致性的條件，雖然Giorgio Szego(2002)認為上述一致性約束仍存在不足，但本文認為滿足上述條件的TailVaR度量方法在實際應(yīng)用方面比VaR更有效，是較為完善的風(fēng)險度量標準。

(三)TailVaR對經(jīng)濟資本極端風(fēng)險的處理

從式(1)可以看出，TailVaR是將大于(1-q)分位數(shù)的損失分布的期望值作為非預(yù)期損失的近似替代，對于尾部不明顯的分布，其極端損失處于損失分布的尾部并發(fā)生概率較小，因此使用TailVaR度量的經(jīng)濟資本與實際所需的經(jīng)濟資本差別較小。但是對于厚尾分布而言，相比于正態(tài)分布等常規(guī)分布極端損失的發(fā)生概率更大，該方法本質(zhì)上沒有排除極端損失，因此與經(jīng)濟資本所表示的非預(yù)期損失可能存在較大差異，相同置信度條件下，TailVaR對經(jīng)濟資本的要求應(yīng)大于VaR對經(jīng)濟資本的要求，而相同的經(jīng)濟資本數(shù)量，TailVaR對應(yīng)的置信度小于VaR使用的置信度。

另外，使用參數(shù)方法的TailVaR度量具有風(fēng)險損失分布依賴性，針對不同的損失分布會得出具有差異性的結(jié)果。因此對于歷史數(shù)據(jù)較準確的分布擬合成為應(yīng)用該方法時較為關(guān)鍵的環(huán)節(jié)，常規(guī)分布可以推導(dǎo)出相應(yīng)的計算公式，對于復(fù)雜的風(fēng)險損失分布難以直接進行計算，需要借助于數(shù)據(jù)模擬與線性規(guī)劃進行求解。

四、基于TailVaR方法的我國保險公司經(jīng)濟資本實證研究

(一)樣本選取與數(shù)據(jù)來源

本文選取2005年至2009年度我國16家保險公司的財務(wù)數(shù)據(jù)(編號1-8為非壽險公司，編號9-10為壽險公司，隱去具體保險公司名稱，結(jié)果備索)。考慮到資產(chǎn)規(guī)模對利潤的影響，本文使用ROA代替利潤，同時考慮到我國保險公司的資產(chǎn)規(guī)模不斷增大，使用近兩個會計年度的平均資產(chǎn)對上述保險公司各個會計年度的ROA進行計算，所有數(shù)據(jù)來自中國保險年鑒(2005-2010)。

表4 我國非壽險保險公司ROA描述性統(tǒng)計

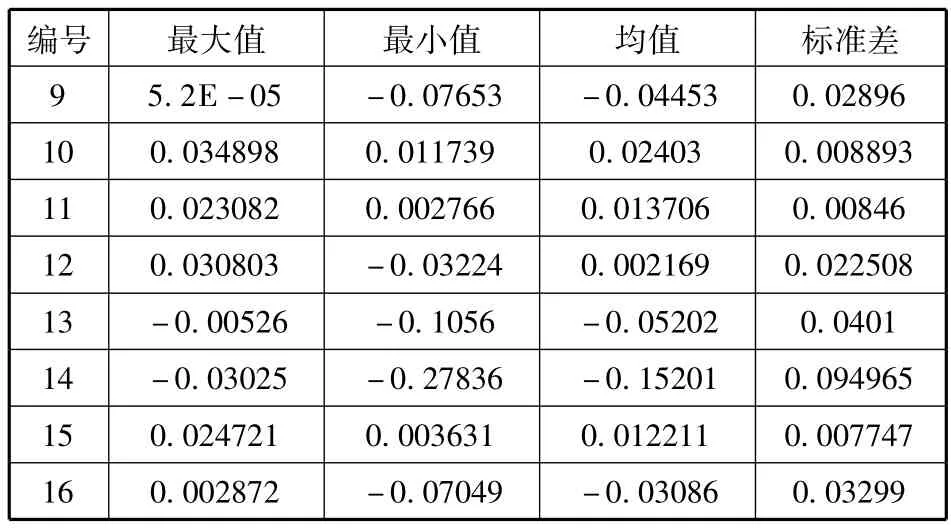
表5 我國壽險保險公司ROA描述性統(tǒng)計

(二)損失率分布假定

目前該領(lǐng)域的研究一般使用ROA近似代替損失率，該處理方法體現(xiàn)了收益與風(fēng)險損失的內(nèi)在關(guān)系——風(fēng)險與風(fēng)險溢價正相關(guān)性，本文仍借鑒這種處理方法。針對我國壽險與非壽險公司的損失率，使用Kolmogorov-Smirnov(K-S)檢驗方法對其進行正態(tài)分布擬合檢驗，由于可供分析的財務(wù)數(shù)據(jù)較少，并考慮到損失分布的厚尾性質(zhì)，本文選取顯著性水平為0.1，P值小于0.1拒絕原假設(shè)，即認為該公司的損失率不服從正態(tài)分布。通過驗證的樣本繼續(xù)使用t檢驗進行樣本的均值檢驗(原假設(shè)為保險公司的損失率為0)，借助R2.12.2對數(shù)據(jù)的K-S檢驗與t檢驗結(jié)果見表6、表7。

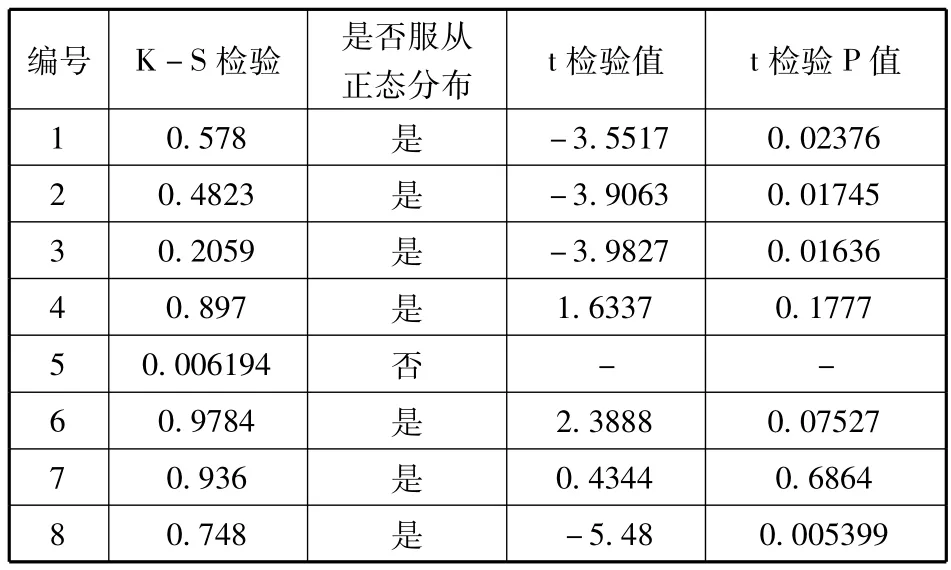
表6 非壽險公司樣本正態(tài)性與均值檢驗

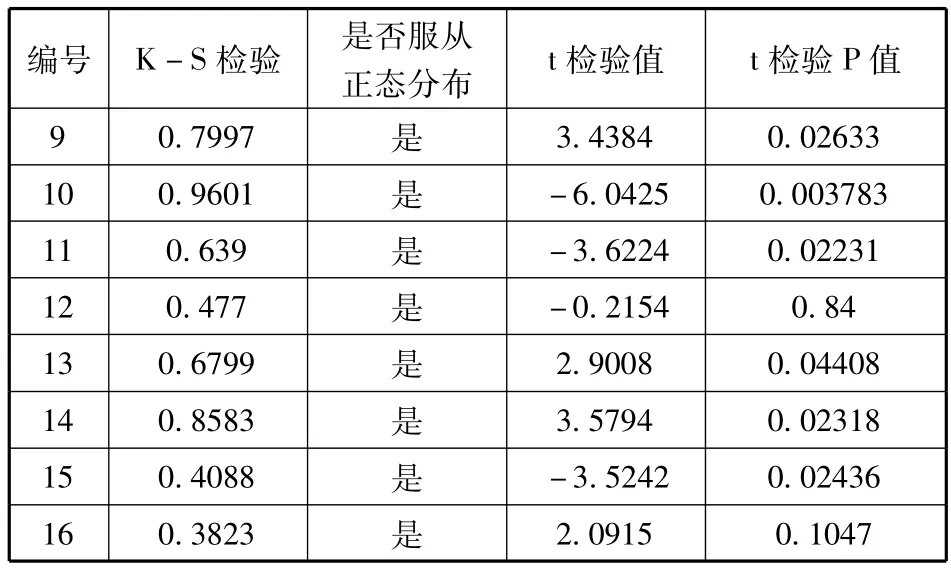
表7 壽險公司樣本正態(tài)性與均值檢驗

K-S結(jié)果顯示，15家保險公司損失率不能拒絕原假設(shè)，可認為其服從正態(tài)分布，t檢驗結(jié)果顯示編號4、7、12、16的保險公司損失率顯著為0。編號為5的財產(chǎn)保險公司其損失率沒有通過正態(tài)性檢驗。之前研究成果將所有保險公司損失率均假定為正態(tài)分布的做法是存在缺陷的，對于編號為5的保險公司損失率只能繼續(xù)進行分布擬合，選擇更合適的分布形式。由于損失率取值一般具有厚尾分布，結(jié)合概率分布直方圖，假設(shè)該保險公司損失率服從Gamma(α，β)，對其進分布擬合得出參數(shù)估計α=0.2，β=3.3，K-S方法的Gamma檢驗結(jié)果P值為0.438，表明Gamma較好地擬合了損失率分布。

對于上文估計的Gamma分布，其不同破產(chǎn)概率下的TailVaR直接計算存在困難，本文使用R估計Gamma分布的在1%、0.5%、0.1%、0.05%、0.01%水平下的上分位點，代入上式求得基于Gamma分布的TailVaR值，具體結(jié)果見表8。

表8 Gamma分布各個置信水平下的TailVaR計算

利用式(2)、式(4)得出正態(tài)分布與Gamma分布的單位資本所需經(jīng)濟資本后，采用2008年與2009年的平均資產(chǎn)計算各個公司所需的總體經(jīng)濟資本，由于存在多種置信水平，本文選取99.9%的置信水平，基本可以考慮到保險公司的多數(shù)風(fēng)險暴露，保證保險公司在較大程度上應(yīng)對非預(yù)期損失，各保險公司的經(jīng)濟資本測算結(jié)果如表9、表10所示。

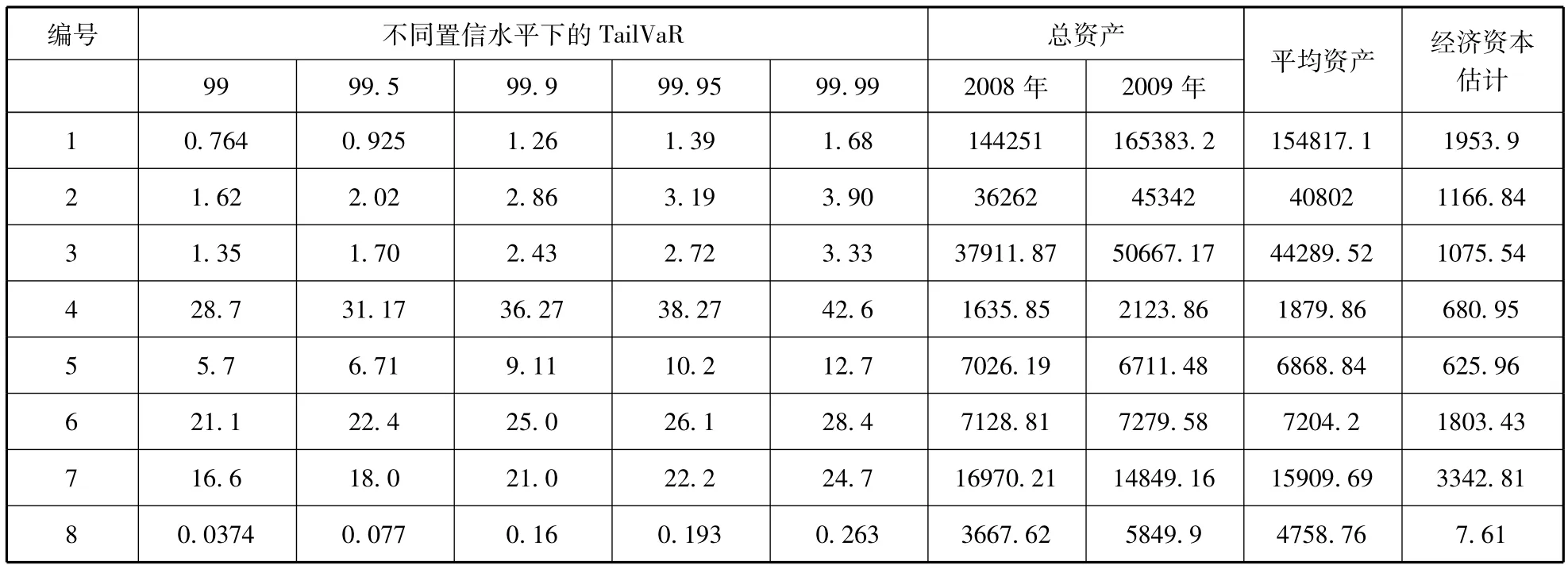
表9 非壽險公司經(jīng)濟資本度量結(jié)果

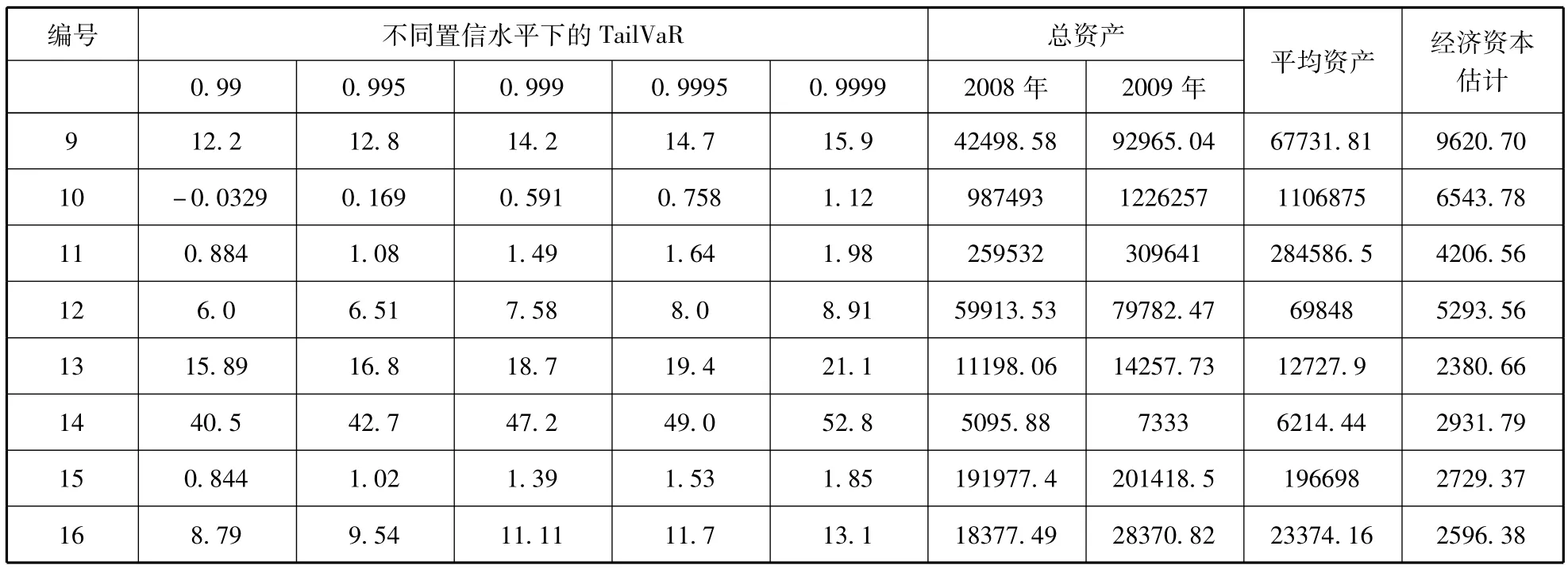
表10 壽險公司經(jīng)濟資本度量結(jié)果

五、結(jié)論

本文選取我國16家保險公司，使用符合風(fēng)險一致性度量的TailVaR方法度量我國保險公司經(jīng)濟資本，各家保險公司由于資本總額不同，實際經(jīng)濟資本絕對數(shù)量不存在可比性，風(fēng)險差異通過同一容忍程度下的TailVaR進行比較。由上述結(jié)果可以看出，中國保險公司的風(fēng)險水平存在較大的差異。觀察各公司的TailVaR可以發(fā)現(xiàn)，風(fēng)險狀況較好的公司編號為 1、8、10、11、15，風(fēng)險處于中等水平的保險公司編號為 2、3、5、7、12、13、16，剩余保險公司面臨較大的意外風(fēng)險沖擊，必須保持較高比例的資金作為經(jīng)濟資本，其中編號14的經(jīng)濟資本占比高達47.2%，可能存在以下方面的問題:經(jīng)濟資本測算的樣本期間較短，使用的數(shù)據(jù)擬合與總體可能存在差距，但是僅僅從標準差也可以看出第14號公司處于損失率的較大波動，反映出公司損失具有較大的不確定性，經(jīng)濟資本的度量結(jié)論實際數(shù)據(jù)可能存在出入，但是排序比較仍然具有實際意義。非壽險公司的平均TailVaR為12.26%，壽險公司的平均TailVaR為12.78%，兩者不存在顯著差異，可以認為在整體層面上，壽險業(yè)務(wù)與非壽險業(yè)務(wù)的整體風(fēng)險差別不大，但是并不排除損失率正態(tài)假設(shè)對該結(jié)果的影響。上述分析結(jié)果表明，各保險公司的風(fēng)險存在較大差異，而基于TailVaR的經(jīng)濟資本方法能夠有效地反映上述差異，因此保險公司應(yīng)該建立以經(jīng)濟資本為核心的企業(yè)風(fēng)險管理框架，更有針對性地預(yù)防企業(yè)自身的風(fēng)險損失，達到提升企業(yè)價值的目的。

本文使用正態(tài)分布與Gamma分布對未通過正態(tài)性檢驗的樣本數(shù)據(jù)進行模擬，隨后基于上述分布計算經(jīng)濟資本，具有一定的創(chuàng)新性。實證結(jié)果表明通過TailVaR計算的經(jīng)濟資本在不同保險公司之間存在較大差異，該方法能夠比較客觀地反映出各保險公司的實際風(fēng)險狀況，是一種較為科學(xué)的風(fēng)險度量方法，應(yīng)得到理論界與實務(wù)界的重視。另外，在衡量保險公司經(jīng)濟資本時，Gamma分布更加注重損失分布的尾部特征，可以修正正態(tài)損失分布的不足，是實際應(yīng)用中的一種有效分布形式，基于其他厚尾損失分布的經(jīng)濟資本度量是今后繼續(xù)研究的方向。

［1］James C.RAROC Based Capital Budgeting and Performance Evaluation;A Case Study of Bank Capital Allocation［R］.Working Paper，Wharton school，1996(9):40-96.

［2］James Lam.Enterprise Risk Management:From Incentives to Controls［M］.Hoboken，N.J.Wiley，2003:26-58.

［3］Harry H P.Measurement of Risk，Solvency Requirements and Allocation of Capital within Financial Conglomerates［R］.AFIR/ICA conference in Cancun in Mexico，2002(3):225-289.

［4］Doherty H A.Integrated Risk Management［M］.New York:McGraw-Hill，2000:1-52.

［5］Michael K Ong.Internal Credit Risk Models:Capital Allocation and Performance Measurement［M］.London Risk，1999.158-177.

［6］Charles Smithson，et al..Result from the 2002 Survey of Credit Portfolio Management Practices［M］.International Association of Credit Portfolio Managers，2002:241-269.

［7］Michael Araten.Current Issue in Estimating Economic Capital for Credit Risk［J］.RMA Journal，2004(3):86-97.

［8］Philippe Jorion.Value at Risk:The New Benchmark for Controlling Derivatives Risk［M］.McGraw-Hill，2009:455-550.

［9］Jonathan Batten and Warren Hogan.A Perspective on Ccredit Derivatives［J］.International Review of Financial Analysis，2002，11(3):251-278.

［10］Michael B Gordy.A Risk-factor Model Foundation for Ratings-based Bank Capital Rules［J］.Journal of Financial Intermediation，2003(10):199-232.

［11］Emmer Susanne，Tasche Dirk.Calculating Credit Risk Capital Charges with the One-factor Model［J］.Journal of Risk，2004，7(5):85-103.

［12］Oldrich Vasicek.Loan Portfolio Value［J］.Risk，2002(12):160-162.

［13］Tor Jacobson，Jesper Lindé and Kasper Roszbach.Credit Risk Versus Capital Requirements under Basel II:Are SME Loans and Retail Credit Really Different？［J］.Journal of Financial Services Research，2005(10):43-75.

［14］Bandyopadhyay Arindam.Assessment of Economic Capital:An Equity Market Approach［J］.National Institute of Bank Management，2008(7):1-6.

［15］Schweizer.Sklar.Probabilistic Metric Spaces［M］.N.J.Wiley，1983:62-108.

［16］Embrechts P，Lindskog，F(xiàn)，McNeil A.Modelling Dependence with Copulas and Applications to Risk Management［J］.Practice，2001(9):329-384.

［17］De Matteis R.Fitting Copulas to data［D］.Zürich:Institute of Mathematics of the University of Zürich ，2001:38-39.

［18］Vanduffel S，Chen X，Dhaene J，et al.Optimal Approximations for Risk Measures of Sums of Lognormals Based on Conditional Expectations［J］.Journal of Computational and Applied Mathematics，2008，221(1):202-218.

［19］Roger B，Nelsen.An Introduction to Copulas［M］.New York:Springer，2005:16-18.

［20］Chavez-Demoulin V，Embrechts P.Quantitative Models for Operational Risk:Extremes，Dependence and Aggregation［J］.Journal of Banking ＆ Finance，2006(10):2635-2658.

［21］張堯庭.連接函數(shù)技術(shù)與金融風(fēng)險分析［J］.統(tǒng)計研究，2002(4):48-51.

［22］Dunbar N.R.Irving:This Is the Way the World Ends［J］.Risk，1998(12):28-32

［23］Schachter，B.Improving Value at Risk with a Precision Measure by Combining Kernel Estimation with Historical Simulation［J］.Review of Derivatives Research，1998(1):371-390.

［24］Embrechts;Paul;Resnick，Sidney，Samorodnitsky.Gennady.Extreme Value Theory as a Risk Management Tool［J］.North American Actuarial Journal，1999(4):30-41.

［25］Moneil，Alexander J.Estimating the Tails of Loss Severity Distributions Using Extreme Value Theory［J］.ASTIN Bulletin，1999，27(1):117-137.

［26］M H Tripp，H L Bradley，R Devett.Quantifying Operational Risk in General Insurance Companies［R］.The Institute of Actuaries ，2004，10(5):919-1012.

［27］Carol Alexander.Bayesian Methods for Measuring Operational Risk［J］.Discussion Papers in Finance，2000.

［28］Jack L King.Operational Risk:Measurement and Modeling［M］.Chichester Wiley，2001:248-262.

［29］Cruz Marcelo.Modeling，Measuring and Hedging Operational Risk，Bayesian Techniques in Operational Risk［M］.NY:John Wiley ＆ Sons Inc.，2002:177-190.

［30］Georges Hubner，et al.Measuring Operational Risk in Financial Institution:Contribution of Credit Risk Modeling［R］.Working Paper，2005.

［31］Giorgio Szego.Measure of Risk［J］.Journal of Banking and Finance，2002(26):1708-1729.

［32］Rockafeller T，Uryasev S.Optimization of Conditional Value-at-risk［J］.Journal of Risk，2000，2(3):21-24.

［33］Artzner P，Delbaen F，Eber J M ，et al.Coherent Measures of Risk［J］.Mathematical Finance ，1999(3):208-226.

［34］Landsman Z，Valdez E A.Tail Conditional Expectations for Elliptical Distributions［J］.North American Actuarial Journal，2003(7):55-71.

［35］Denault D.Coherent Allocation of Risk Capital［J］.Journal of Risk，2005(1):7-21.

［36］Furman E，Landsman Z.Risk Capital Decomposition for Multivariate Dependent Gamma Portfolio［J］.Insurance:Mathematics and Economics ，2005，37(7):635-649.

［37］Vernic R.Multivariate Skew-normal Distributions with Applications in Insurance［J］.Insurance:Mathematics and E-conomics ，2006，38(2):413-426.

［38］許大志，鄭祖康.非參數(shù)方法在金融風(fēng)險管理模型中的應(yīng)用［J］.系統(tǒng)工程，1999(5):20-27.

［39］王春峰，萬海暉，張 維 .金融市場風(fēng)險測量模型——VaR［J］. 系統(tǒng)工程學(xué)報，2000(1):67-75.

［40］田新時，劉漢中，李 耀.基于DeltaGamma正態(tài)模型的VaR計算［J］.系統(tǒng)工程，2002(5):92-96.

［41］杜本峰.基于Bootstrap方法的風(fēng)險度量模型及其實證分析［J］.統(tǒng)計研究，2004(1):49-54.

［42］劉曉星.銀行操作風(fēng)險度量方法比較研究［J］.財經(jīng)問題研究，2006(1):61-67.

［43］彭建剛，吳 思，張麗寒.國外兩種商業(yè)銀行經(jīng)濟資本計量方法的比較分析［J］.上海金融，2008(7):62-66.

［44］楊繼光，劉海龍.商業(yè)銀行組合信用風(fēng)險經(jīng)濟資本測度方法研究［J］.金融研究，2009(4):143-158.

［45］田 玲，張 岳.基于GARCH模型的我國保險公司經(jīng)濟資本度量［J］.保險研究，2010(3):37-41.

［46］田 玲，羅添元，王正文.基于Copula函數(shù)的保險公司經(jīng)濟資本配置研究［J］.保險研究，2011(6):51-55.

［47］梁 凌，譚德俊，彭建剛.CreditRisk+模型下商業(yè)銀行經(jīng)濟資本配置研究［J］.經(jīng)濟數(shù)學(xué)，2005(9):221-228.

［48］滕 帆.中國保險公司經(jīng)濟資本估算［J］.統(tǒng)計與信息論壇，2005(6):33-36.

［49］李 博，徐樅巍.基于TailVaR的中國商業(yè)銀行經(jīng)濟資本度量研究［J］.合肥工業(yè)大學(xué)學(xué)報:社會科學(xué)版，2009(12):7-11.

［50］朱建平.中國保險業(yè)經(jīng)濟資本管理的實證研究［J］.南京審計學(xué)院學(xué)報，2009，6(2):35-39.

［51］竇爾翔，熊燦彬.基于RAROC的我國金融機構(gòu)的風(fēng)險與效率分析［J］.國際金融研究，2011(1):83-89.