基于集成支持向量機的故障診斷方法研究

王金彪， 周 偉， 王 澍

(上海飛機設計研究院，上海 200235)

0 引言

近年來，集成學習是機器學習中的一個研究熱點，它通過訓練多個基分類器，并將結果按一定的方法進行集成，可以顯著地提高分類系統的泛化能力，許多學者對其進行了廣泛的研究，許多學者開始致力于研究集成學習的理論基礎和進行算法設計［1－2］。

支持向量機 (Support Vector Machines，SVM)是基于統計學習理論的一種適合高維、小樣本數據分類的學習器。和傳統的學習機器相比，它可以獲得和可利用樣本相匹配的學習能力，從而可以具有很好的推廣能力，在模式識別方面有很重要的應用［3］。SVM具有較好的泛化能力和穩定性(其結果不隨訓練次數發生變化)。但是實際應用中SVM也有一些缺點:首先，SVM訓練問題實際上是一個凸二次優化問題，在解優化問題是采用了逼近算法，這會使結果不準確;其次，SVM的性能很大程度上取決于核函數和模型參數的選擇，目前還沒有一個特別有效的方法可以準確找到最優參數，這也會導致支持向量機的訓練結果不是最優的。

本文擬通過集成學習的方法來提高支持向量機的泛化能力，提高支持向量機的識別精度，并應用到故障診斷中。

1 集成學習

1.1 概述

集成學習一般包含3個要素:基分類器類型、基分類器生成方法和結論生成方法。常用的基分類器有決策樹、K近鄰分類器、神經網絡、支持向量機等。基分類器可以為同種類型，也可以為不同類型，分別稱為同構集成和異構集成，其中同構集成為研究重點，異構集成研究得較少。本文采用的基分類器為支持向量機。同構集成中基分類器的生成方法主要有以下3大類。

1)對訓練集進行處理。

如Breiman提出的Bagging方法，其思想是對訓練集有放回地抽取訓練樣本，從而為每一個基分類器都構造出一個跟訓練集同樣大小但又各不相同的訓練集，從而訓練出不同的基分類器，進而構建一個多分類器系統［4］。

2)對數據特征進行處理。

其思想為對于具有多特征的數據集，通過抽取不同的輸入特征子集分別進行訓練，從而獲得不同的基分類器，把這些分類器的分類結果適當整合能夠獲得比任何一個基分類器的分類精度都要高的分類器，其中子空間法為其典型代表方法［5］。

3)通過隨機擾動產生具有差異性的基分類器。

隨機擾動法的思想是在每個基分類器的學習過程之中引入隨機擾動，使得學習出來的每個基分類器都不同，如果基分類器對隨機擾動比較敏感，那么隨機擾動法可以有效地產生多個不同的基分類器。這種方法比較容易在人工神經網絡集成學習上進行。對于人工神經網絡，使用后向傳遞算法來進行學習的時候對于每個神經網絡的初始權值進行隨機分配，則產生的基分類器會有很明顯的不同;又如，對于支持向量機集成，可以擾動支持向量機模型中的核函數的參數，進而產生具有差異性的基分類器。

1.2 集成學習的有效性

Hansen和Salamon經過研究發現，假設集成由N個獨立的基分類器構成，每個基分類器的分類錯誤率為p，采用絕對多數投票法，當參與集成的各基分類器的錯誤是不相關的，那么集成的誤差為［6］

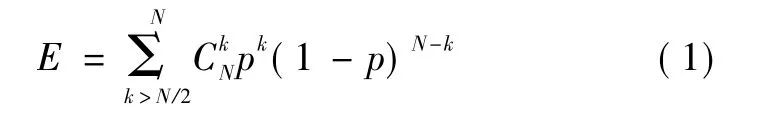
當基分類器之間的錯誤相關時，相關系數為0≤α≤1，將模型簡單化，假設各個基分類器之間的錯誤相關部分相同，那么集成后的誤差為

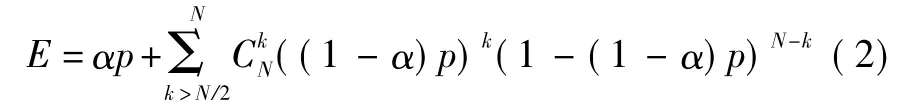
當各個基分類器的分類錯誤率均為p=0.2，相關系數為0，0.25，0.50，0.75，1 時(相關系數為0，即各基分類器的錯誤是完全不相關;相關系數為1，即各基分類器完全相同;相關系數越大意味著基分類器之間的差異性越小)，集成后的分類錯誤率如圖1所示。

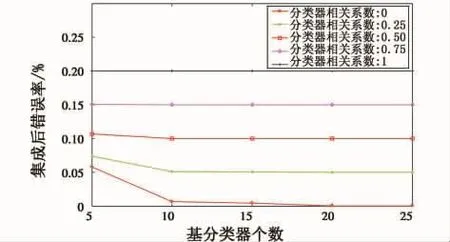
圖1 集成分類器錯誤率與相關系數的關系Fig.1 The relationship of the error recognition rate and correlation coefficient

上述簡化模型雖不能完全反映出集成后的錯誤率與基分類器間差異性的關系，但一定程度上表明了兩者的聯系，即通過集成學習得到的多分類器系統對于基分類器有一定的要求，否則多分類器系統的泛化能力與單分類器系統相比不一定能得到提高，基分類器一般應滿足以下兩個原則［7］:

1)基分類器的精度應達到一定要求，對太低的精度的基分類器進行集成不會有一個好的結果，但是基分類器精度太高的話，又會影響基分類器之間的差異性;

2)各個基分類器之間應有一定的差異性，差異性是影響集成效果的重要因素，舉一個極端的例子來說，如果我們對10個相同的基分類器進行集成，顯而易見，泛化能力不會有任何的提高，因為這10個基分類器之間的差異性為零，這導致集成后沒有效果。

總之，基分類器的精度越高、差異性越大，那么集成后的泛化能力越好，從圖1中可以看出，當各個基分類器相同時(即相關系數為1，差異性最小)，集成后泛化能力沒有提高;隨著各個基分類器之間差異性的增大(相關系數為0時，差異性最大)，集成后泛化能力提升越大。另外，從圖1中可以看出，隨著基分類器個數的增多，集成誤差越來越小，當基分類器數達到15以后，集成后誤差變化不大;且隨著基分類器個數的增多，模型也越復雜，訓練、測試需要的時間也越多，因此本文在兩者之間取一個折衷，基分類器數目取為15個。

1.3 支持向量機的穩定性

本文采用的基分類器為支持向量機，經典集成學習算法Bagging對于神經網絡(Neural Network，NN)有很好的提升作用，為了了解Bagging對支持向量機的作用，本文進行了下述實驗，對于Image數據集，保持模型參數不變，分別隨機去除10%、20%、30%、40%、50%、60%、70%、80%、90%的數據，形成9個新的數據集，每種情況下對數據集進行了隨機劃分(按照6:4的比例，60%為訓練集，40%為測試集)，進行了10次隨機劃分，支持向量機識別結果如圖2所示，神經網絡識別結果如圖3所示。

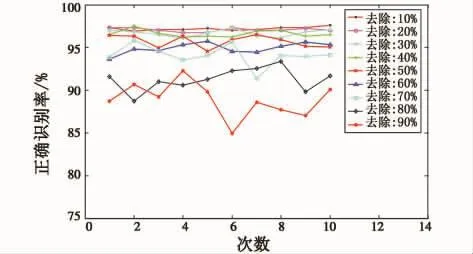
圖2 SVM在Image數據集上的正確識別率Fig.2 The correct recognition rate of SVM

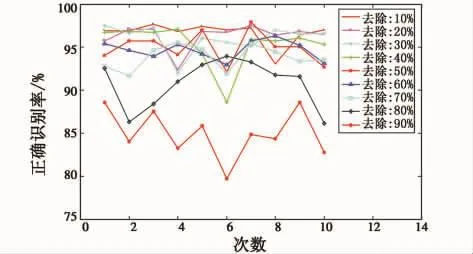
圖3 NN在Image數據集上的正確識別率Fig.3 The correct recognition rate of NN

為了更好地定性說明問題，對數據集進行了100次隨機劃分(按照6:4的比例，60%為訓練集，40%為測試集)，計算了100次識別結果的正確識別率的均值和方差，如表1所示，方差即表征分類器對數據變化的敏感程度。

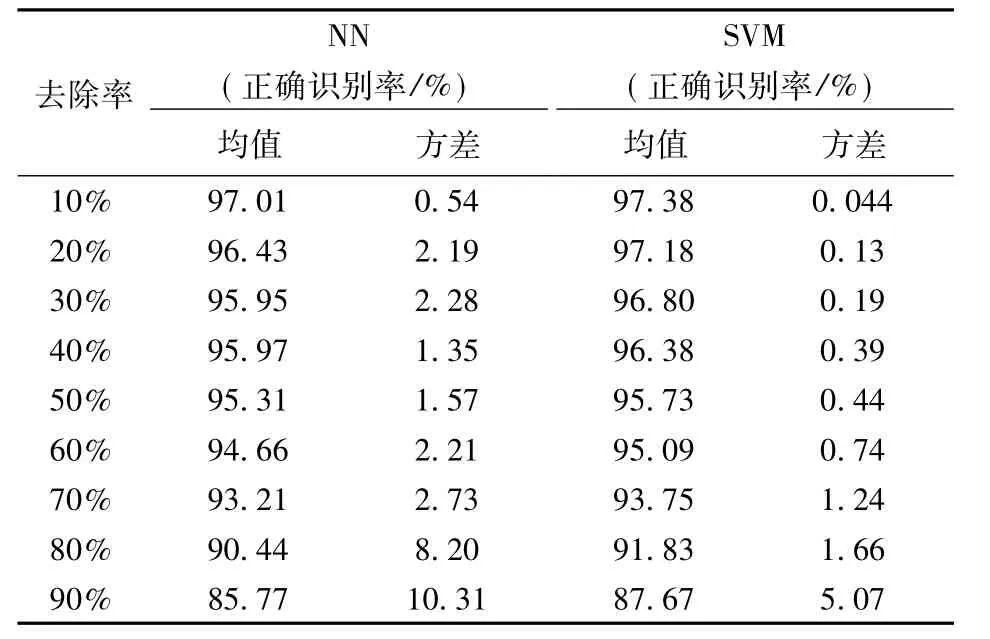
表1 NN與SVM的穩定性比較Table 1 The stability of NN and SVM

在表1中，在所有的去除率情況下，SVM的識別率均高于NN方法，且前者100次計算的方差遠遠小于后者，這說明SVM相對于神經網絡分類器來說是一種穩定的分類器，對數據擾動不敏感，也就是說它滿足了集成學習對基分類器要求的第一個條件:基分類器要有好的分類精度，卻沒有滿足第二個條件——基分類器要有較大的差異性。而Bagging方法通過擾動數據集，來形成不同的訓練集，進而來訓練具有差異性的基分類器，因而這種方法對穩定性較差的分類器算法如神經網絡效果比較好，而對于穩定性較好的SVM的泛化能力提升不大。

2 雙重擾動集成支持向量機

對于支持向量機集成，為了更好地擴大基分類器的差異性，提高集成后的正確識別率，本文采用了同時擾動數據特征和數據集的方法，來生成基分類器，來達到提高基分類器差異性的目的。

子空間法是一種通過擾動特征來得到不同的訓練集，進而得到具有差異性的基分類器的一種集成學習方法。其中的一個關鍵環節是:如何對特征進行擾動。本文將特征評估算法——Relief算法應用到特征擾動中，首先通過特征評估算法計算各個特征的權重，接著利用此權重向量，通過輪盤賭法產生一系列特征子集，進而得到一系列不同的訓練集，使得訓練集具有差異性，最后得到一系列基分類器，形成一個多分類器系統。

Relief算法是從訓練集中隨機選擇一個樣本R，然后從同類樣本中尋找最近鄰樣本H，稱為NearestHit，再從和其不同類的樣本中尋找最近鄰樣本M，稱為NearestMiss，然后對于每維特征，如果R和H在其上的距離小于R和M上的距離，則說明此維特征對區分同類和不同類的最近鄰是有益的，則應該增加該特征的權重;反之，如果R和H在其上的距離大于R和M上的距離，則說明此維特征對區分同類和不同類的最近鄰是有害的，則應該減小該特征的權重。Relief算法提出時針對于處理類別數為兩類的數據的分類問題，后來Kononenko擴展了Relief算法得到了ReliefF算法，ReliefF可以解決多類問題以及回歸問題。實際上故障診斷中分類問題一般為多類分類，因此需要利用Relief擴展后的算法ReliefF。ReliefF算法在處理多類問題時，不是從所有不同類樣本集合中統一選擇最近鄰樣本，而是從每個不同類別的樣本集合中選擇最近鄰樣本，并且不是選擇一個最近鄰樣本，而是選擇k個最近鄰樣本［8－9］。ReliefF算法偽代碼如下所述。

通過上述RelidfF算法得到的權重向量，利用輪盤賭法進行特征的選擇，雙重擾動集成支持向量機算法偽代碼如下所述。

3 試驗驗證

3.1 標準數據集驗證

為了了解雙重擾動集成算法對支持向量機泛化能力的提升作用，本文對于雙重擾動集成支持向量機在標準數據集上進行了實驗。其中集成支持向量機中基分類器個數為15，對于多類識別問題，采用一對一方法將兩類支持向量機擴展為多類支持向量機。所有支持向量機核函數選為徑向基核函數，最優參數通過網格法得到。子空間集成支持向量機和支持向量機在測試集上的正確識別率如表2所示，均值和方差為算法重復100次的結果(每次對數據進行按6:4的隨機劃分)。

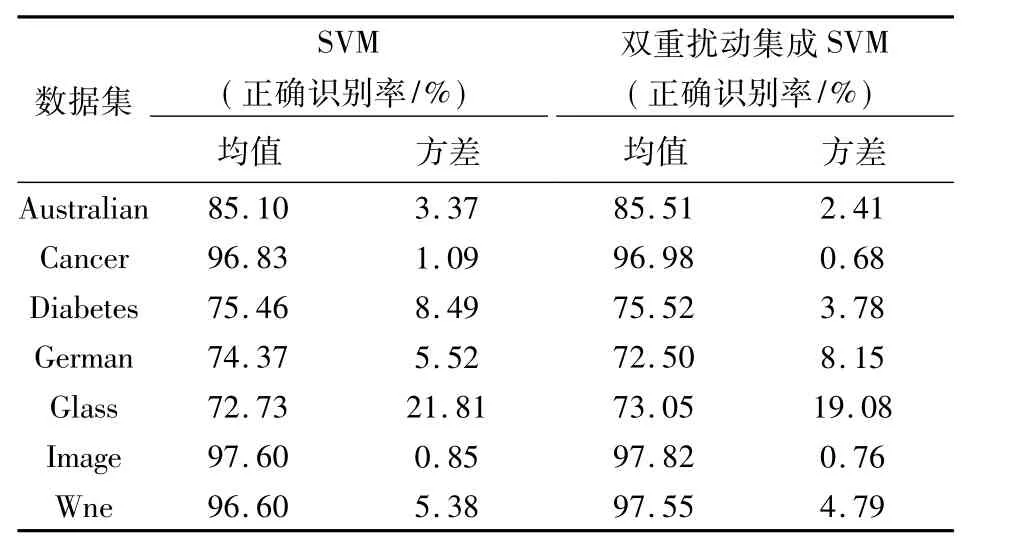
表2 識別結果對比分析Table 2 Comparison of the recognition results

由表2可以看出，除了German數據集，在其他6個數據集上，雙重擾動集成SVM較SVM正確識別率都有不同程度的提高，并且方差都比SVM小，說明雙重擾動集成支持向量機比SVM有更強的穩定性，泛化能力較SVM有了提升。雙重擾動集成SVM在這6個標準數據集上的正確識別率比子空間集成SVM的正確識別率高，究其原因，是由于雙重擾動法采用了兩種機制對數據進行了擾動，因此集成后結果較好。

3.2 故障數據驗證

為驗證雙重擾動集成支持向量機在故障診斷中的作用，對在立式試驗臺上得到的正常狀態、不平衡狀態、碰磨狀態、半頻渦動狀態4種試驗數據，進行了分類識別。

故障診斷第一步，通過時域特征提取和小波包特征提取方法對信號進行分析，提取所需要的特征向量。對信號進行了時域特征提取，分別提取了波形指標、峰值指標、脈沖指標、裕度指標、偏斜度指標、峭度指標以及峰峰值，作為特征向量中的7個參數。再加上由小波包分解得到的16個特征，總共23個特征組成一個樣本。從這4種狀態中總共提出500個樣本，其中正常狀態100個樣本，不平衡狀態200個樣本，碰磨狀態100 個樣本，半頻渦動100 個樣本［10－11］。

故障診斷第二步，利用雙重擾動集成支持向量機和支持向量機對其進行分類識別，其中訓練集為300個樣本，測試集為200個樣本，基分類器個數為15個，支持向量機核函數為徑向基核函數，核函數參數通過網格法得到，識別結果如表3所示。試驗結果表明，雙重擾動法提高了支持向量機的正確識別率。

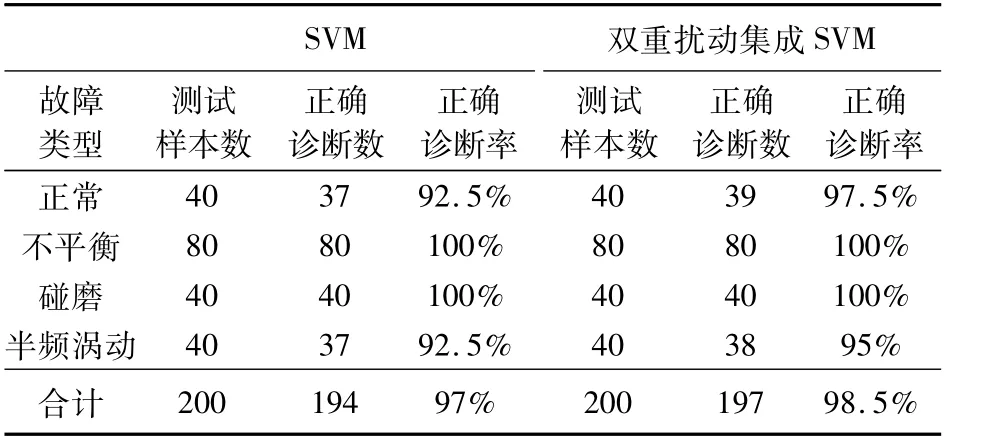
表3 故障診斷結果對比分析Table 3 Comparison of the fault diagnosis results

4 結論

本文對集成學習方法在支持向量機上的應用進行了研究，通過模擬試驗證明了支持向量機的穩定性，說明了傳統集成學習方法對其泛化能力提升有限，進而提出了雙重擾動法。采用了適合的特征評估算法——ReliefF算法得到權重向量，進而通過輪盤賭法得到子空間法所需要的特征子集，并與Bagging算法結合起來，形成了雙重擾動法，在標準數據集及實際故障數據上進行了試驗，結果表明，雙重擾動法較好地提升了支持向量機的泛化能力。

［1］ DIETTERICH T G.Machine learning research:Four current directions［J］.AI Magazine，1997，18(4):97-136.

［2］ VALENTINI G，MASULLI F.Ensembles of learning machines［R］.Neural Nets WIRN Vietri-02，Series Lecture Notes in Computer Sciences，2002.

［3］ VAPNIK V.統計學習理論的本質［M］.張學工，譯.北京:清華大學出版社，2000.

［4］ BREIMAN L.Bagging predictors［J］.Machine Learning，1996，24:123-140.

［5］ ZHANG Y Q，RAJAPAKSE J C.Feature selection for ensemble learning and its application［M］.New Jersey:John Wiley ＆ Sons，2008.

［6］ HANSEN L K，SALAMON P.Neural network ensembles［J］.IEEE Transaction on Pattern Analysis and Machine Intelligence，1990，12(10):993-1001.

［7］ DIETTERICH T G.Ensemble learning［J］.The Handbook of Brain Theory and Neural Networks，2002:1-9.

［8］ KIRA K，RENDELL A A.The feature selection problem:Traditional methods and a new algorithm［C］//Proceedings of the Ninth National Conference on Artificial Intelligence，1992:129-134.

［9］ KONONENKO.Estimation attributes:Analysis and extensions of RELIEF［J］.Proceedings of the 1994 European Conference on Machine Learning，1994(784):171-182.

［10］ 胡橋，何正嘉，張周鎖.基于提升小波包變換和集成支持向量機的早期故障智能診斷［J］.機械工程學報，2006(8):16-22.

［11］ 張岐龍，單甘霖，段修生，等.基于小波支持向量機的模擬電路故障診斷［J］.電光與控制，2010，17(5):66-69.