中心距誤差對重合度的影響研究
2012-09-03 08:39:38蘇州市職業大學機電工程系施雄泉
湖北農機化 2012年6期
蘇州市職業大學機電工程系 施雄泉
0 引言
齒輪傳動是各種機械設備中常用的零件,在使用中總希望齒輪的承載能力高、傳動平穩。其中一重要影響因素是重合度,實際使用中總希望重合度大些,但由于齒輪制造、安裝時總有誤差,故會影響重合度的數值。本文主要探討中心距誤差對重合度的影響。
1 漸開線齒輪的傳動重合度

ε稱為重合度,它表明同時參與嚙合的輪齒對數。
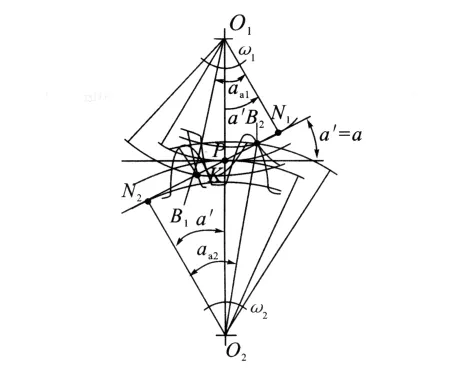
圖1 齒輪傳動的重合度
由(1)知,基圓上的齒距pb=πm由圖1知
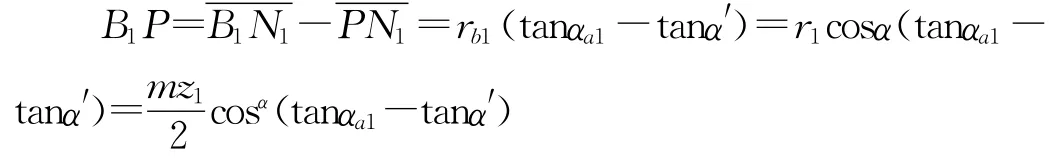
式中:αa1為小齒輪的齒頂圓壓力角,α′為嚙合角,m為模數
同理:
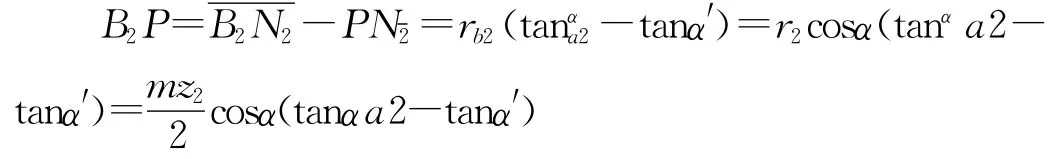
式中αa2為大齒輪的齒頂圓壓角

式中:α為理論中心距,α′為實際中心距,Δ為中心距誤差
由上述諸式可知,重合度與模數無關,與小齒輪齒數、傳動比及中心距安裝誤差有關。
分別取Z1為17、20、25、30,傳動比為1、2、4、6,用Matlab繪圖工具繪圖,圖2~圖5為中心距誤差與重合度的關系曲線。
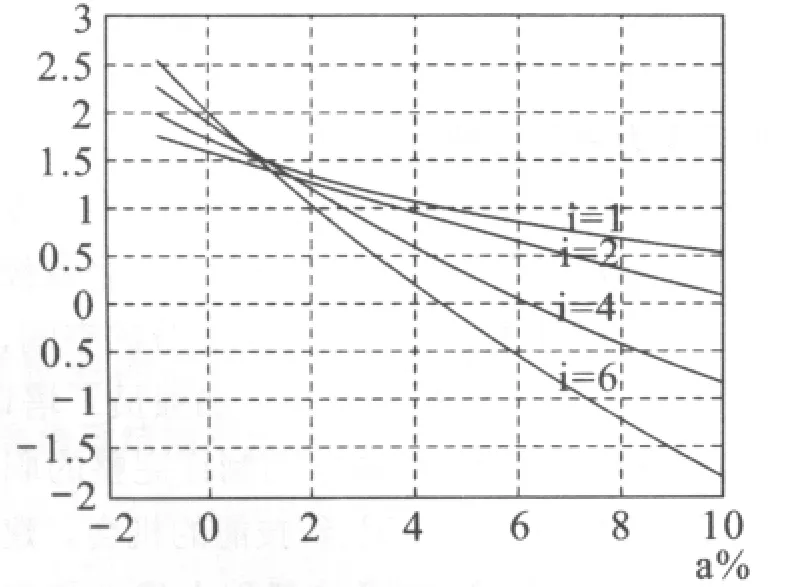
圖2 Z1=17時的重合度與中心距誤差關系
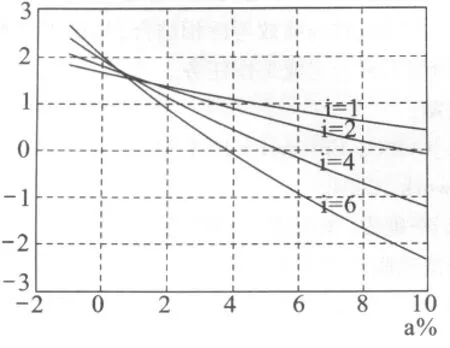
圖3 Z1=20時的重合度與中心距誤差關系
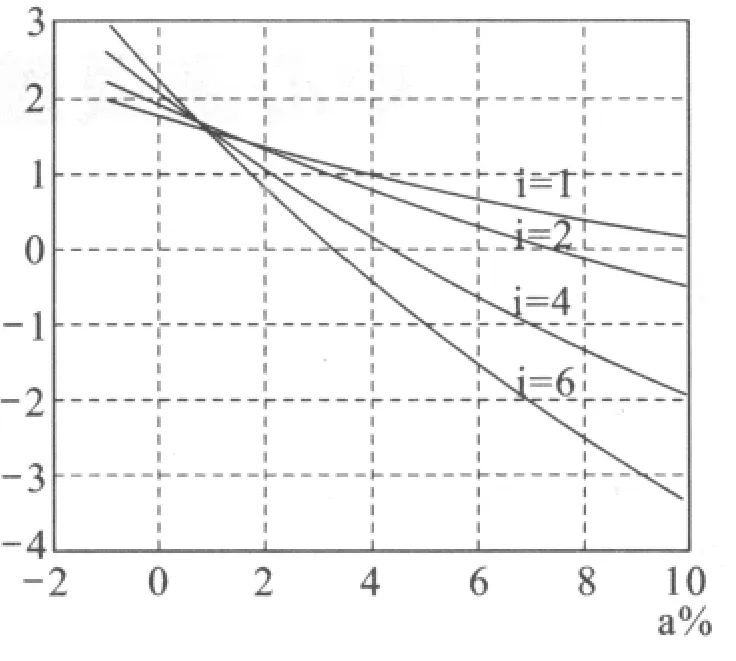
圖4 Z1=25時的重合度與中心距誤差關系
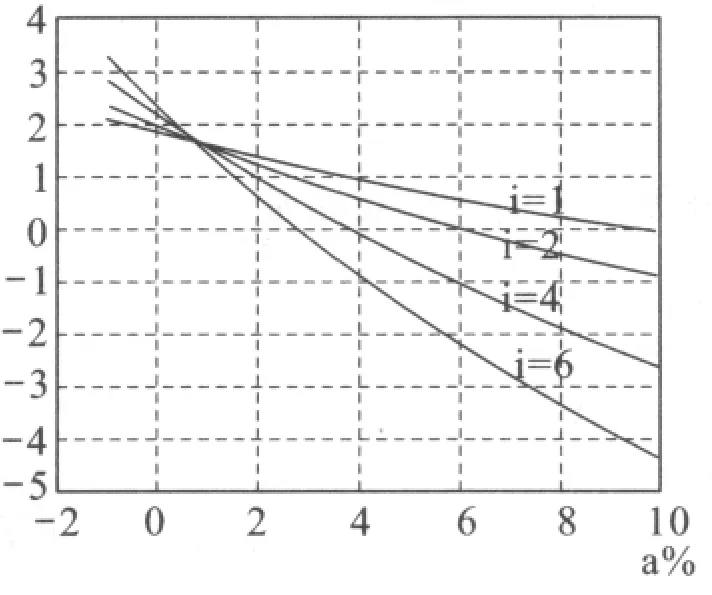
圖5 Z1=30時的重合度與中心距誤差關系
2 結論
由圖2~圖5知,當中心距誤差小于0時,傳動比愈大,重合度愈大,但實際上此時無法安裝,估無意義;當中心距誤差大于0而小于1%時,傳動比愈大,重合度愈大;當中心距誤差大于1%時,傳動比愈大,重合度愈小;當中心距誤差大于1.5%時,重合度將小于1,此時無法保持連續傳動,所以建議在實際設計時,中心距誤差不要超過1%。
[1]孫恒,陳作模.機械原理[M].北京:高等教育出版社,2001.
[2]黃錫愷,鄭文緯.機械原理[M].北京:高等教育出版社.1989.
[3]阮沈勇.MATLAB程序設計[M].北京:電子工業出版社.2004.

