基于近似模型的兩級集成系統協同優化方法

蔣 平 匡 玲 邵新宇 肖 蜜

華中科技大學數字制造裝備與技術國家重點實驗室，武漢，430074

0 引言

復雜工程系統（如飛機、船舶、汽車、機械裝備等）的設計通常涵蓋多個相互耦合的學科，為了對多學科耦合進行有效處理，以獲得最優的系統設計方案，Sobiesczanski－Sobieski［1］提出了多學科設計優化（multidisciplinary design optimization，MDO）方法。

MDO方法也稱MDO策略，是當前MDO領域的研究熱點。MDO方法按照是否對系統進行分級處理，可分為單級MDO方法和多級MDO方法兩大類。相比單級 MDO方法，多級MDO方法更符合復雜工程系統設計的組織模式，利于進行學科間的并行設計和分布式計算。常用的多級MDO方法主要有：協同優化（collaborative optimization，CO）方法、并行子空間優化（concurrent subspace optimization，CSSO）方法、分層目標傳遞（analytical target cascading，ATC）方法和兩級集成系統綜合（bi－level integrated system synthesis，BLISS）方法。其中，BLISS中的BLISS2000被認為是目前全局優化性能最強的多級MDO方法［2］。但BLISS2000方法仍然存在比較大的改進空間，其中，作為子系統級影響系統級的權值系數w的數學意義并不明確，而且若優化問題存在大量耦合，將它作為系統級設計變量，那么系統級設計變量的維數將大大增加，導致搜索難度和計算量加大。CO方法雖然從結構形式上較好地解決了復雜工程系統設計的組織復雜性問題，但容易出現難于收斂和陷入局部收斂的現象。為此，結合BLISS2000和CO特點的兩級集成系統協同優化（bi－level integrated system collaborative optimization，BLISCO）方法被提出［3］，從組織形式和協調分解方面更好地解決了大規模多學科耦合問題。

在復雜工程系統的多學科設計優化中，往往涉及眾多高精度的仿真分析模型，如結構有限元分析模型、氣動分析模型，以及計算流體動力學分析模型等，這使得計算成本大大增加；同時，在學科仿真分析中，不可避免地會產生一些數值噪聲，這將降低求解算法的收斂速度，甚至導致無法獲得全局最優解。因此，有必要在設計過程中引入近似模型來代替高精度的仿真分析模型，降低反復調用高精確仿真分析模型的計算成本，縮短設計周期，平滑數值噪聲，獲得整體最優的設計方案。

基于以上分析，本文提出了一種BLISCO與近似模型技術相結合的MDO方法，通過在BLISCO方法中引入近似模型來降低計算復雜度，加快算法收斂速度，避免數值噪聲，提高設計優化效率。并且通過具體的算例，驗證了本文所提出方法的有效性和可行性。

1 基于近似模型的BLISCO方法

1.1 BLISCO方法

BLISCO是一種兩級優化方法，分為系統級優化和子系統級優化。系統級優化負責協調子系統之間的差異，子系統級優化負責最小化耦合輸出狀態變量對系統目標函數的綜合影響。BLISCO方法保留了CO方法的協同機制，而用子系統耦合輸出狀態變量的加權和代替子系統一致性約束作為其優化的目標函數。BLISCO方法在形式上更類似于BLISS2000方法，不同的是BLISCO方法通過嚴格的推導，明確了w的數學定義，從而在系統級消除了w變量，降低了系統級設計變量的維數，不需要進行包含系統級優化和子系統級優化的系統迭代過程。

對涉及N個子系統的多學科設計優化問題，采用BLISCO方法所得到的數學模型如下［4］。

（1）子系統級優化。在系統級給定 ｛zshare，zy｝的條件下，第i個子系統優化問題可表述為

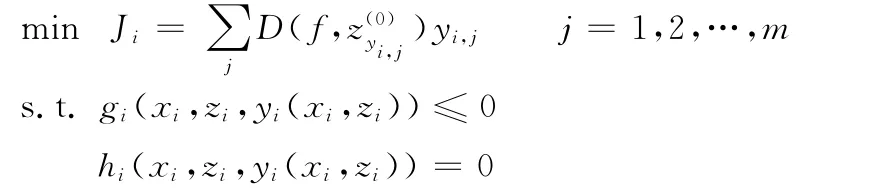
其中，zi是系統級設計變量，包括｛zshare，zy｝，zshare為系統級共享設計變量，zy為對應子系統耦合狀態變量的系統級耦合設計變量；yi，j是子系統i的第j個耦合狀態變量；xi是子系統的局部設計變量；D（f，）是系統級目標函數對初始耦合設計變量的導數；gi和hi分別表示第i個子系統的不等式約束和等式約束。如果第i個子系統的狀態變量包含系統級目標f，那么該子系統的目標函數就是系統級目標函數，這體現了該子系統對系統級目標函數的全部影響。D（f，）可通過兩種方式獲得：當系統級目標函數為耦合設計變量的顯函數時，可通過解析法直接獲得導數信息而不需要進行子系統分析；當系統級目標函數為耦合設計變量的隱函數時，可采用先通過子系統優化得到約束對應的拉格朗日乘子，然后進行最優靈敏度分析的方法獲得導數信息［5］。

（2）系統級優化。即

其中，y＊為子系統優化后獲得的耦合狀態變量值；C為耦合設計變量和耦合狀態變量之間的一致性約束；gs和hs分別為系統級的不等式約束和等式約束。

1.2 近似模型

在設計優化過程中，不可避免地要對設計空間進行有效探索。復雜系統的MDO問題，存在著計算復雜、組織復雜、模型復雜以及信息交換復雜等問題，直接將單學科設計優化中常用的設計空間搜索優化算法應用于多學科分析中是不切實際的［6］。

近似模型技術就是用現有的簡單模型擬合原始的復雜設計空間，可以減少設計優化過程中的計算次數、預計輸入輸出參數之間的關系，避免算法陷入局部最優。同時，近似模型技術與優化算法的不同組合，還可以提供新的優化問題求解方法。近似模型技術作為學科分析和優化算法之間的接口，已得到了廣泛的應用［7－8］。目前常用的近似模型包括響應面模型、徑向基神經網絡模型、泰勒序列逼近模型以及Kriging模型［9］。構建近似模型的一般流程如圖1所示。

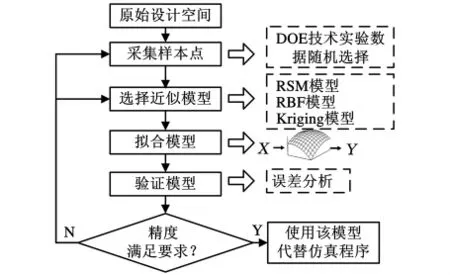
圖1 構建近似模型的一般流程圖

1.3 近似模型與BLISCO方法的結合

本文將近似模型與BLISCO方法相結合，提出了基于近似模型技術的BLISCO方法，算法結構如圖2所示。

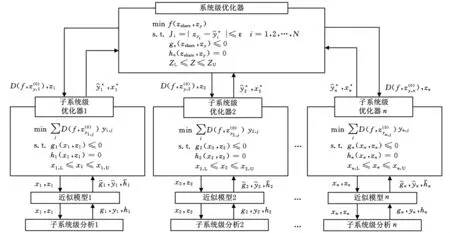
圖2 基于近似模型的BLISCO方法基本結構

在圖2所示算法結構中，包括子系統級優化、子系統級優化、子系統級分析及近似模型的建立。zshare是系統級共享設計變量；zy是系統級耦合設計變量；zi是系統級傳遞到第i個子系統的系統級設計變量目標值，zi∈ ｛zshare，zy｝；xi是該子系統的局部設計變量；yi，j是對應于系統耦合設計變量zyi，j的子系統i的第j個子系統耦合狀態變量；D（f，）是系統級目標函數對耦合設計變量的導數，上標0代表初始耦合設計變量、x＊i是經過子系統優化后獲得的狀態變量和局部設計變量值是通過近似技術建立的子系統等式和不等式約束以及狀態變量的函數模型；Ji為系統級耦合設計變量目標值與優化后的耦合狀態變量值之間的一致性約束，為了加快收斂速度，以絕對值小于ε的不等式約束代替等式約束。其中子系統近似模型的構建在子系統級優化之前，這與BLISS2000對子系統優化的結果建立近似模型不同，不需要進行復雜的系統分析，不必針對優化結果擴展和收縮響應面邊界；另外，在對子系統分析建立的近似模型中也包括約束條件，去除了約束的數值噪聲，避免了系統級優化的結果在子系統級不可行的問題，同時減少了系統級循環的次數。流程中子系統分析的目的只是為了建立近似模型，故分析只針對設計空間中采集的少量樣本點進行，與BLISCO方法相比，避免了每一次系統優化都要進行繁多的子系統分析，從而大大減少了計算量，提高了優化效率，同時對子系統建立近似模型消除了設計空間的數值噪聲，可以更高效地找到系統全局最優方案。

2 算例分析

2.1 齒輪減速箱優化問題

齒輪減速箱優化問題（speed reducer problem，SRP）是 NASA（national aeronautics and space administration）評估 MDO方法性能的十大標準算例之一［10］。該問題包含齒輪設計和軸設計，目標是在滿足齒輪的彎曲應力和接觸應力以及軸的位移和應力等約束條件下使得減速箱的質量最小。它的數學模型［11］如下：

文獻［12］給出了該問題的最優解x＊＝ （3.5，0.7cm，17，7.3cm，7.71cm，3.35cm，5.29cm）T，最優目標值f（x＊）＝2994kg。

根據基于近似模型的BLISCO算法，將該問題分為系統級和兩個子系統級，分解如下。

系統級：

子系統2：

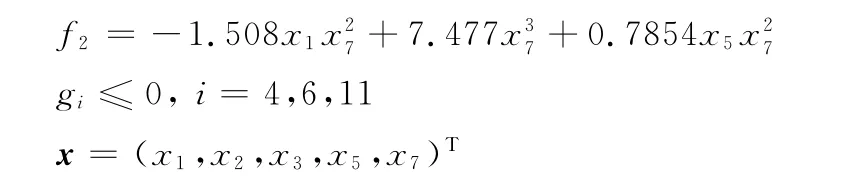
由于子系統的狀態變量之間不存在耦合關系，故引入虛擬耦合設計變量。其中系統級設計變量Z＝｛x1，x2，x3，zy1，zy2｝，子系統1局部設計變量X1＝｛x4，x6｝，子系統2局部設計變量X2＝｛x5，x7｝。考慮到該算例函數并不復雜，且響應面模型具有較好的全局近似能力，計算量也不大，故選用二次多項式響應面作為近似模型，具體的算法結構如圖3所示。選取五個不同的初始點，各點取值如表1所示。

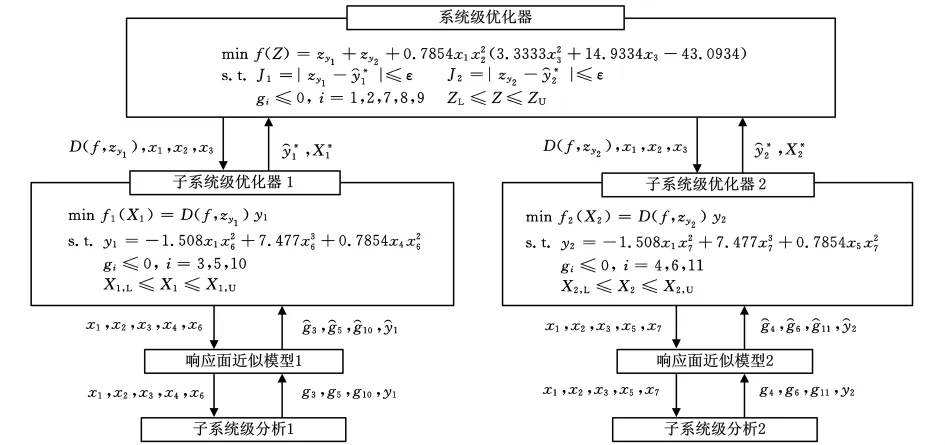
圖3 齒輪減速箱的優化算法結構圖

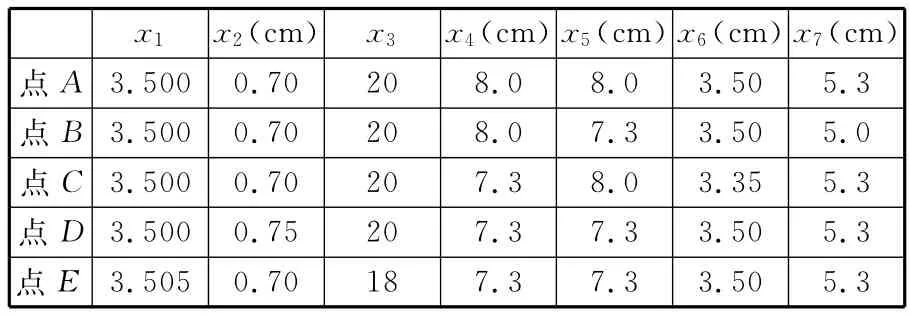
表1 五個不同的初始點的取值

在子系統設計空間中，采用隨機選取的方法，選取72個樣本點，建立二次多項式響應面模型分別如圖4和圖5所示。

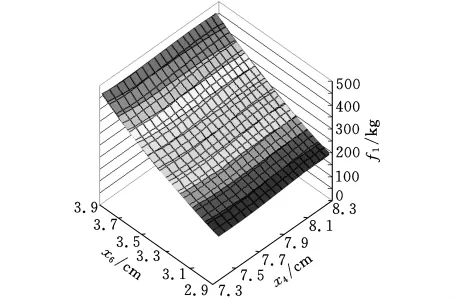
圖4 子系統1的二次多項式響應面近似

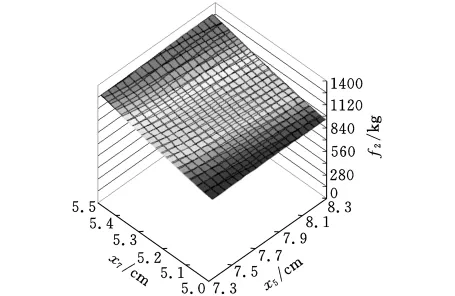
圖5 子系統2的二次多項式響應面近似

用多學科設計優化軟件iSIGHT建立優化模型，系統級和子系統級均使用序列二次規劃優化算法，一致性約束的ε取為0.005。對于5個不同的初始點，用原BLISCO算法求得的優化結果如表2所示。選取同樣的初始點和優化算法，響應面近似模型與BLISCO算法結合后求得的優化結果如表3所示。

表2 原BLISCO算法優化結果

表3 近似技術與BLISCO結合后的優化結果

比較分析表2和表3可以看出，無論使用原BLISCO算法還是使用基于近似模型的BLISCO方法，對于不同的初始值，該算例均收斂到穩定的優化解，充分證明了該優化方法的有效性。另外，使用近似模型的BLICO方法雖然系統迭代次數有稍許增加，但相比原BLISCO算法需要1000多次的子系統分析，而建立近似模型只進行了72次的子系統分析而言，優化速度得到了很大提高；由于對子系統的約束和狀態變量均建立了近似模型，消除了設計空間的數值噪聲，基于近似模型的BLISCO方法獲得了比原算法更好的全局最優解，這又體現了該方法的高效性和準確性。且相比其他優化算法如 BLISS2000算法［13］（均值2994.355 955kg）、基于Kriging近似的ECO算法［14］（均值2997.117kg），基于近似模型的BLISCO方法的效果也更好。

以樣本點E為例，基于近似模型的BLISCO方法獲得系統級和子系統級目標的優化歷程如圖6所示。

為了考慮近似模型精度對優化結果的影響，對前面構造的近似模型增加了18個樣本點，重新構造響應面模型，優化后得到的結果如表4所示。

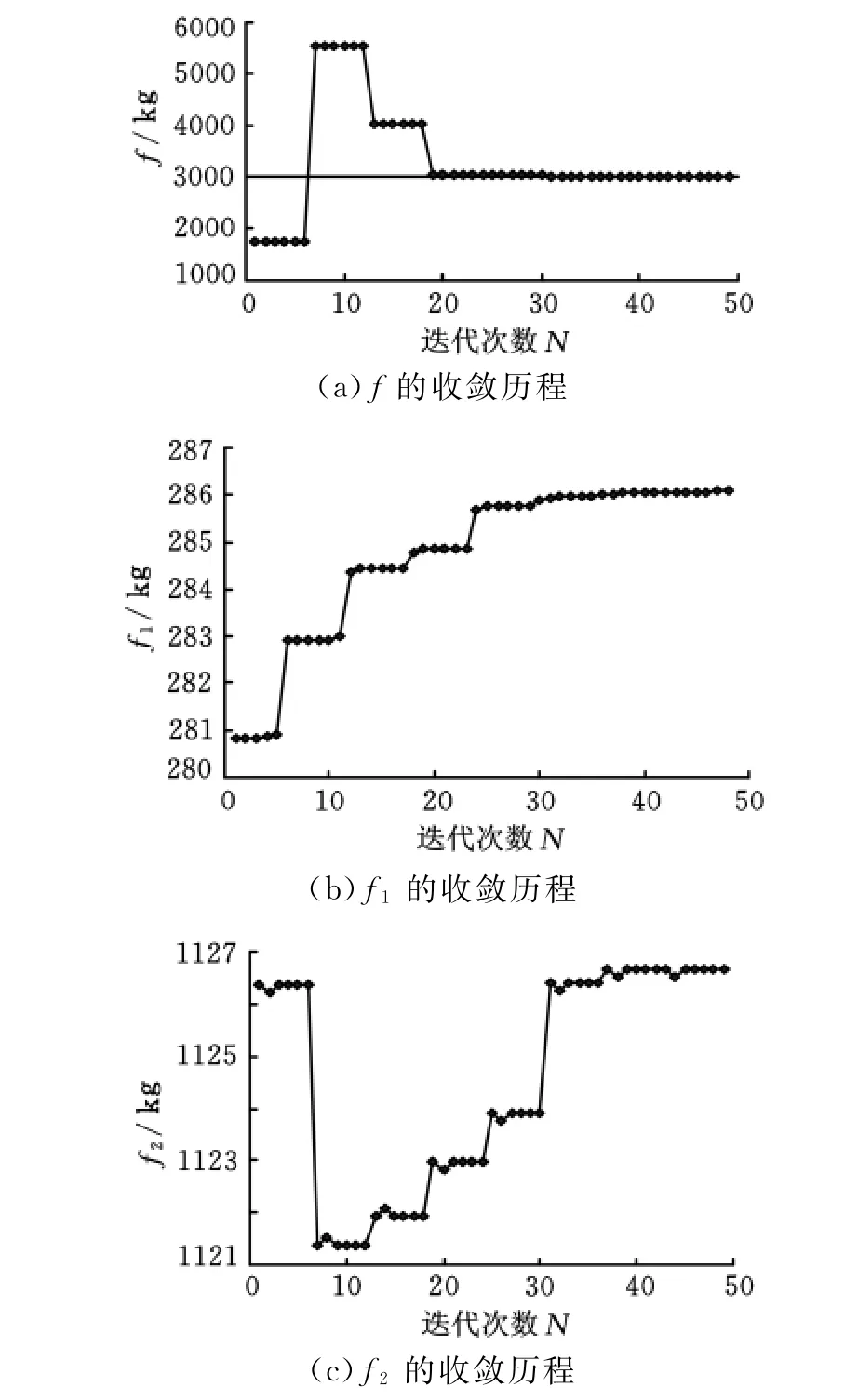
圖6 系統級和子系統級目標的收斂歷程

表4 增加樣本點后的優化結果

從表4可以看出：增加近似模型精度后，該優化策略獲得全局最優解的能力更強，獲得的優化解2994.065 23kg與文獻［12］給出的最優解2994kg十分接近，這說明近似模型建立的精確度越高，該優化策略獲得的結果越準確。

2.2 經典耦合函數優化問題

經典耦合函數是Sellar測試CSSO／RS優化過程的MDO算例［15］，它是一個典型的非線性強耦合優化問題，其數學模型的描述如下：

根據基于近似模型的BLISCO算法，首先確定系統級設計變量和子系統級局部設計變量。y1和y2中均含有x1、x3，且y1和y2之間存在耦合關系，故確定系統級設計變量Z＝｛x1，x3，zy1，zy2｝，子系統級局部設計變量為x2。因為y2中不含局部設計變量，不需要對其進行優化，可將其并入系統級優化，子系統1的設計變量X1＝｛x2｝。

最終算法分解如下。

系統級：

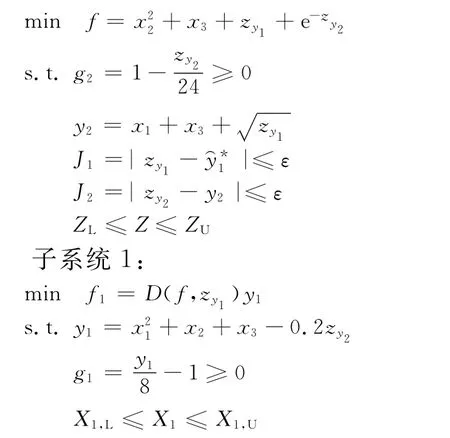
運用多學科設計優化軟件iSIGHT對其建立優化模型，y1函數比較簡單，故它的函數近似也采用響應面模型。選取4個初始點如表5所示。

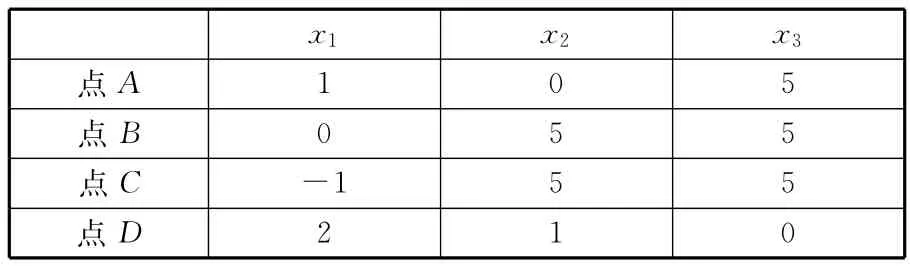
表5 四個不同的初始點

用拉丁超立方試驗設計方法選30個樣本點，對子系統1建立二次響應面模型如圖7所示。

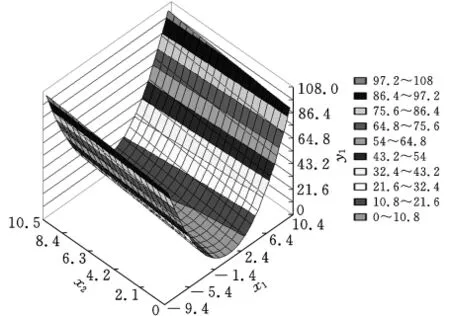
圖7 子系統1的近似模型

選取15個樣本點對子系統輸出響應和約束進行近似誤差分析，結果如圖8所示。

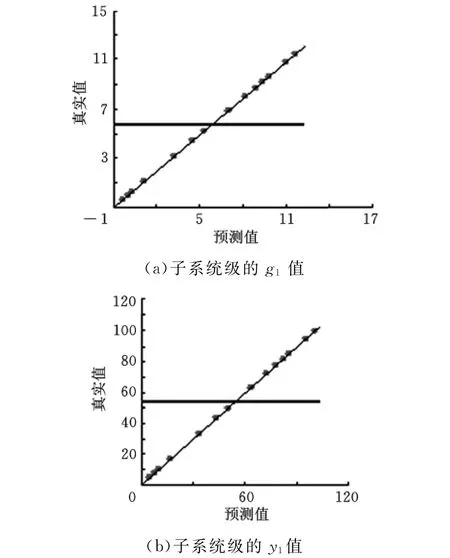
圖8 子系統輸出和約束真實值和近似值的誤差分析

該響應面模型的預測值與實際值趨于一致，輸出響應和約束的總誤差數量級為10－17，故對子系統1建立的響應面近似模型完全滿足精度要求。

系統級優化采用廣義簡約梯度法，子系統級優化采用NLPQL優化算法，一致性約束的ε取為0.005。對各初始點進行設計優化，用原BLISCO算法求得的結果如表6所示，將近似模型與BLISCO算法結合后獲得的優化結果如表7所示。

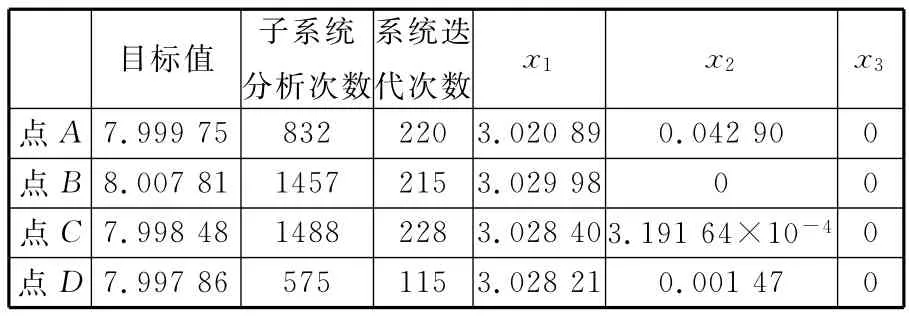
表6 原BLISCO算法優化結果

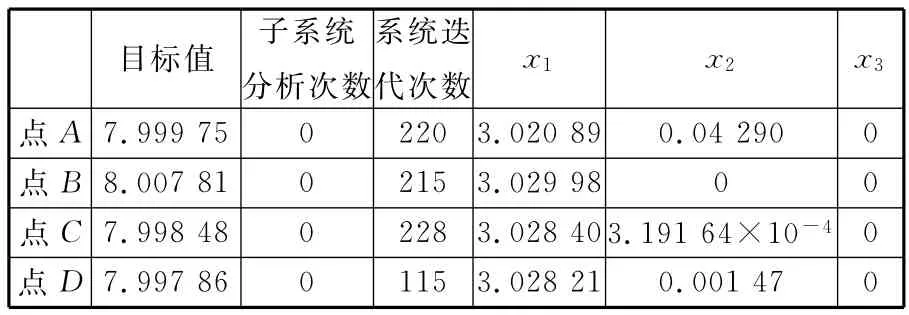
表7 近似技術與BLISCO結合后的優化結果

由表7可知，建立近似模型后的系統迭代次數和優化結果同采用精確分析模型的BLISCO算法相同，但避免了反復的子系統分析過程，計算量大大降低，優化效率明顯提高。

為了提高非線性約束問題的收斂速度，一致性約束中用含ε的不等式約束代替了嚴格的等式約束。本文選取了不同數值的ε來研究ε的取值大小對優化結果的影響，當ε取0.05、0.0005、0.000 005時，使用基于近似模型的BLISCO方法求得的優化結果分別如表8～表10所示。

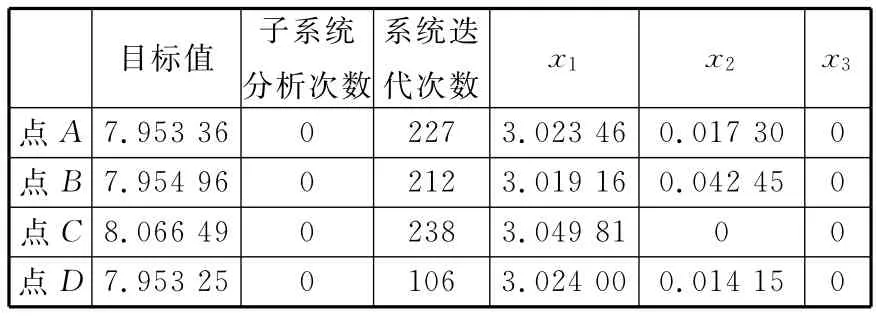
表8 當ε＝0.05時，近似技術與BLISCO結合后的優化結果

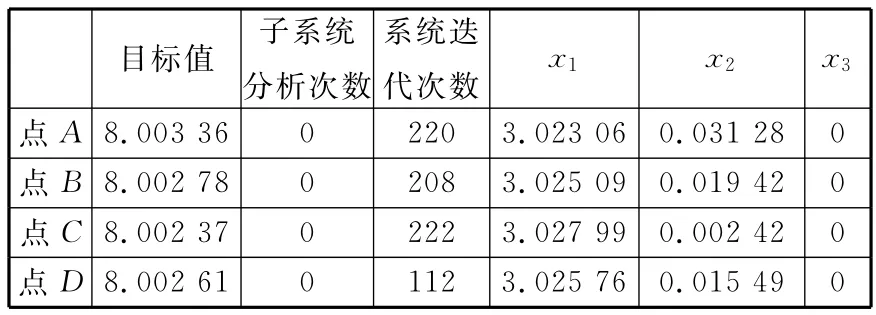
表9 當ε＝0.0005時，近似技術與BLISCO結合后的優化結果

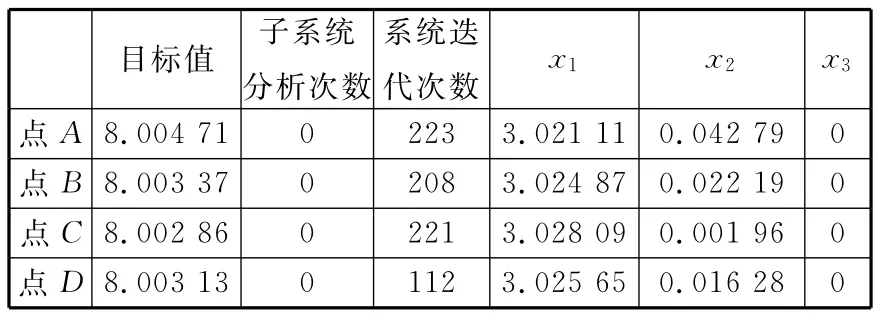
表10 當ε＝0.000 005時，近似技術與BLISCO結合后的優化結果

可以看出，對于不同的ε取值，系統都得到了收斂的優化結果，驗證了一致性約束中用不等式約束代替嚴格等式約束的可行性。且當一致性約束的允許容差減小時，優化結構隨初始值變化的波動降低，結果穩定性較好。另外從表中結果來看，進行優化得到最優解的計算量與容差值大小的選取沒有太大關系，與初始值的選取相關。

3 結語

本文提出了一種基于近似模型的BLISCO方法，該方法不但保留了BLISCO方法的優點，而且通過用近似模型代替昂貴的子系統高精度仿真模型，達到了提高大規模復雜MDO問題優化效率的目的。通過齒輪減速器算例和經典耦合算例，驗證了當子系統之間存在／不存在耦合，以及選取不同初始點條件下，基于近似模型的BLIS－CO方法的可行性和高效性，并獲得了比原BLISCO方法以及相關文獻所提出方法更好的優化結果。同時，本文對系統級一致性約束的不同允許容差進行了研究，驗證了一致性約束中用不等式約束代替嚴格等式約束的可行性，且允許容差越小，收斂得到的最優解隨不同初始點的波動越小，即優化結果更穩定。

目前，本文所采用的算例較為簡單，從模型構建效率出發，采用了響應面模型作為近似模型。在以后的研究中，將根據問題特征采用精確度或效率更高的近似模型，并擬將所提出的基于近似模型的BLISCO方法應用到更復雜的工程系統設計中。

［1]Sobiesczanski－Sobieski J.A Linear Decomposition Method for Optimization Problem－Blueprint for Development［R］.Hampton：NASA Technical Memorandum，1982.

［2]Xu L，Yan L，Chen X Q，et al.Enhanced Bi－level Integrated System Synthesis 2000 （EBLISS 2000）［C］／／50th AIAA／ASME／ASCE／AHS／ASC Structures Structural Dynamics and Materials Conference.New York：American Institute of Aeronautics and Astronautics Inc.，2009：1－15.

［3]趙敏，崔維成.BLISCO方法在載人潛水器設計中的應用［J］.船舶力學，2009（2）：259－268.

［4]趙敏.兩級集成系統協同優化方法及其在深海空間站總體概念設計中的應用［D］.上海：上海交通大學，2009.

［5]Barthelemy J F，Sobieszczanski－Sobieski J.Optimum Sensitivity Derivatives of Objective Function in Nonlinear Programming［J］.AIAA Journal，1983，21（6）：913－915.

［6]王振國，陳小前，羅文彩，等.飛行器多學科設計優化理論與應用研究［M］.北京：國防工業出版社，2006.

［7]Sakata S，Ashida F，Zako M.Structural Optimization Using Kriging Approximation［J］.Computer Methods in Applied Mechanics and Engineering，2003，192（7／8）：923－939.

［8]Gusciora P H，Foss A S.A Reduced－order Model of a Fixed－bed Reactor Based on a Novel Application of the Taylor Dispersion Approximation［C］／／American Control Conference.Atlanta，1988：1058－1063.

［9]鐘毅芳，陳柏鴻，王周宏.多學科綜合優化設計原理與方法［M］.武漢：華中科技大學出版社，2006.

［10]Padula S L，Alexandrov N M，Green L L.MDOTest Suite at NASA Langley Research Center，AIAA－1996－4028［R］.New York：American Institute of Aeronautics and Astronautics，1996.

［11]Kodiyalam S.Evaluation of Methods for Multidisciplinary Design Optimization（MDO），CR－1998－208716［R］.Hampton：NASA，1998.

［12]Azarm S，Li W C.Multi－level Design Optimization Using Global Monotonicity Analysis［J］.Journal of Mechanisms，Transmissions，and Automation in Design，1989，111（2）：259－263.

［13]蔡偉，陳小前，姚雯.基于加速收斂BLISS的不確定性多學科設計優化［C］／／高金伍，王國俊.第六屆中國不確定系統年會論文集.香港：Global－Link Publisher，2008：25－30.

［14]Xiao M，Gao L，Qiu H B，et al.An Approach Based on Enhanced Collaborative Optimization and Kriging Approximation in Multidisciplinary Design Optimization［J］.Advanced Materials Research，2010，118／120：399－403.

［15]Sellar R S，Batill S M，Renaud J E.Response Surface Based，Concurrent Subspace Optimization for Multidisciplinary System Design，AIAA－1996－0714［R］.New York：American Institute of Aeronautics and Astronautics，1996.