基于灰色BP神經網絡的質心數據處理方法

張 憲 鐘 江 吳 暉 趙章風

浙江工業大學，杭州，310014

0 引言

發展山區丘陵農業機械化的關鍵之一在于選擇適宜于山區丘陵作業的體積小、重量輕、性能高的農業機械［1－2］。小型農業作業機作為山區丘陵地帶農業作業的主力機具，其質心高度參數和其他位置參數將直接影響整機對作業環境的適應性能、整機的動力性能、作業和行駛的穩定性、側翻安全性以及加速時的動態響應等。因此，質心位置的確定在小型作業機的整機設計中具有舉足輕重的地位，也是小型農業作業機整機設計的關鍵。

1 三點支撐質心位置測試系統的測試原理

質心位置參數一般需要通過質心測試系統試驗獲得。本文基于三點支撐質心位置測試系統來測試質心高度［3］。其原理如圖1所示。三個支點呈等腰三角形布置，每個支點上設置一個稱重傳感器，底邊兩個支點通過球關節與平臺上表面連接。測試時，頂端支點在伺服電機的驅動下做上下運動，通過稱重傳感器讀取三個支點處的數據，經計算得到被測物體的質心位置參數。

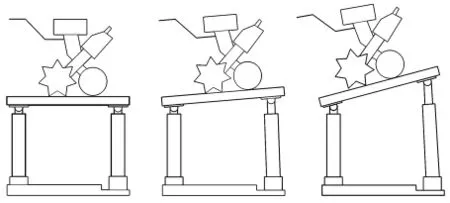
圖1 三點支撐質心位置測試系統測試過程示意圖

通過理論研究可知［3］：頂端支點升降，測試平臺與水平面形成一個傾斜角。質心高度坐標測試的精度隨傾斜角的增大而提高。

由于在測試過程中，傾斜角度大于被測小型作業機和測試平臺之間的摩擦角，故被測小型作業機將產生滑移，較為危險；同時，測試系統存在隨機誤差和系統誤差，為獲得較高精度的質心高度數據，需要進行大量的重復測試。在保證測試精度的前提下，為提高測試效率，本文構建一種具有較高精度的質心高度預測模型，通過有限次小角度測試獲得的數據，可以預測得到較高精度的質心高度參數。

2 質心高度預測模型的構建流程

質心高度預測模型的構建受到兩方面的約束：一是不可能包括所有因素；二是很難確定通過測試獲取的含有誤差的參數之間的精確關系［4－5］。采用兩種或多種預測模型構建技術的組合，可以盡可能多地利用測試獲得的數據中所包含的有效信息。

由理論研究可知［3］：質心高度相對誤差曲線為指數曲線，其通式為

式中，y為質心高度相對誤差；x為三點支撐質心位置測試系統中產生平臺傾斜的升降桿位移；a、b為系數。

由式（1）可以看出，平臺的傾斜角度與測試數據的平均值亦呈指數曲線分布。由于灰色系統理論對于構建指數型的模型具有獨特的優勢，同時它具有“貧信息”、建模簡單的優點，因此本文采用灰色系統理論進行質心位置預測模型的構建。但是，灰色系統理論還存在缺乏自學習能力、自組織能力和自適應能力，對非線性信息的處理能力較弱，且不能包括所有影響因素等缺陷。BP神經網絡技術具有“大樣本”、非線性處理能力及學習能力強、能夠快速收斂等特征。根據灰色系統理論中灰數的定義可知，BP神經網絡的輸出實際上是灰數，即BP神經網絡包含灰色內容，可以用灰色系統理論對其進行考察，反之用BP神經網絡技術來研究灰色系統也是可行的［6－8］。由于灰色系統理論與BP神經網絡技術具有上述特點，所以，將灰色系統理論與BP神經網絡進行有機的結合，構建基于灰色BP神經網絡技術的質心位置預測模型是可行的。

基于灰色系統理論，可以在“貧信息”條件下建模，但由于“貧信息”和系統非線性信息處理能力較弱的缺陷，使得所建模型誤差較大，雖然可以通過對初始值和背景值的改進來提高精度［9］，但在實際應用中，采用灰色模型直接預測所得數據的真實性值得商榷。而采用BP神經網絡技術，基于在試驗范圍內灰色模型計算出的數據，對質心位置進行進一步的預測，可以很好地彌補上述不足。

將灰色模型與BP神經網絡在模型中按串聯方式結合［10］，即將灰色模型的輸出作為BP神經網絡的輸入，則質心位置預測模型構建流程如圖2所示。圖2中，ξ1、ξ2分別為基于GM（1，1）灰色模型和基于BP神經網絡模型的擬合精度；δ1、δ2分別為第一級GM（1，1）灰色模型和第二級BP神經網絡模型的設定精度。

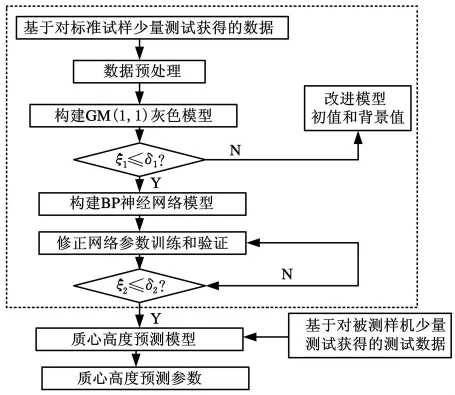
圖2 數據預測模型構建流程圖

在質心位置預測模型的構建中，將已知重量和質心位置的標準試樣在測試系統上進行有限次、小角度測試，對所得原始數據進行預處理，剔除壞值，以減小粗大誤差對預測精度的影響。然后基于灰色系統理論，采用GM（1，1）灰色模型進行第一級質心位置預測模型的構建。該模型的構建，本質上是采用灰色模型對原始數據進行擬合，擬合精度將決定該模型對質心位置預測的精度。在該模型構建過程中，需要將預測結果與已知試樣的質心位置進行對比，通過修改模型初始值和背景值來提高模型的擬合精度。當基于灰色系統理論獲得的第一級預測模型達到設定的精度后，基于該模型預測的數據以及影響測試精度的主要因素——傾斜角，構建第二級基于BP神經網絡技術的質心位置預測模型，通過對網絡參數的修正和訓練，使其預測結果達到規定的精度，至此，質心高度預測模型構建完成。

3 試驗平臺的搭建與試驗數據

3.1 試驗平臺的搭建

小型三點支撐質心位置測試系統方案如圖3和圖4所示，主要由機械系統和控制系統組成。機械系統包括測試平臺、底座、升降推桿、稱重傳感器、位移傳感器和球鉸等，其中頂端支點可在較大范圍內上下升降，以調整測試平臺的傾斜角；控制系統包括計算機、數據采集卡等。系統所采用的稱重傳感器和位移傳感器的性能參數見表1和表2。

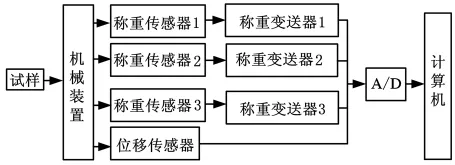
圖3 測試系統總體方案

圖4 驗證用試驗臺

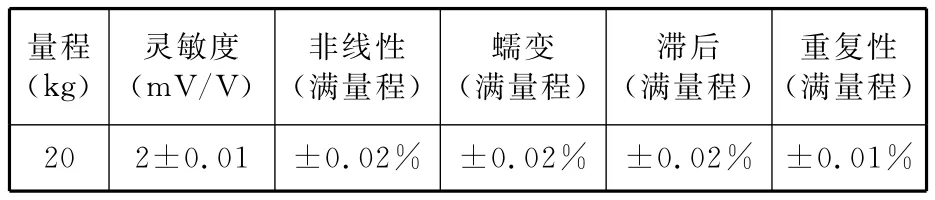
表1 稱重傳感器參數表

表2 位移傳感器參數表

在試驗過程中，首先調整三個支點的高度，將測試平臺調整成水平狀態；之后放上標準試樣，調整頂端支點的高度，使測試平臺與水平面成某一傾斜角，并讀取三個稱重傳感器和位移傳感器的測量值，代入質心計算公式［3］，可得到標準試樣質心位置的測試值。

3.2 試驗數據

本次試驗已知標準試樣的質心高度為45mm。考慮到在小型作業機質心位置的實際測試中，質心測試平臺的傾斜角度不能太大，故在試驗中選取與實際測試相近的傾斜角（5°～8°），測試時，每隔0.2°進行一次數據采集，從5°到8°和從8°到5°來回各測5次并取其平均值，代入質心位置計算公式，計算出的標準試樣的質心高度測試數據和理論高度的相對誤差見表3中“測試數據”一欄。

從表3中可以看出，由于測試次數較少，數據具有一定的離散性，同時，當角度較小時，其相對誤差較大；隨著測試角度的增大，相對誤差變小。

4 質心高度預測模型的構建與預測

4.1 基于灰色系統理論的灰色模型的建立

根據灰色系統理論，有如下預測模型（GM（1，1）灰色模型）：

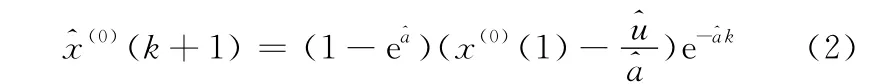
將表3的測試數據代入式（2），可以獲得基于灰色系統理論的初步質心位置預測模型：

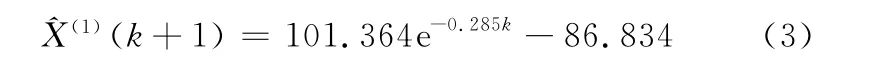
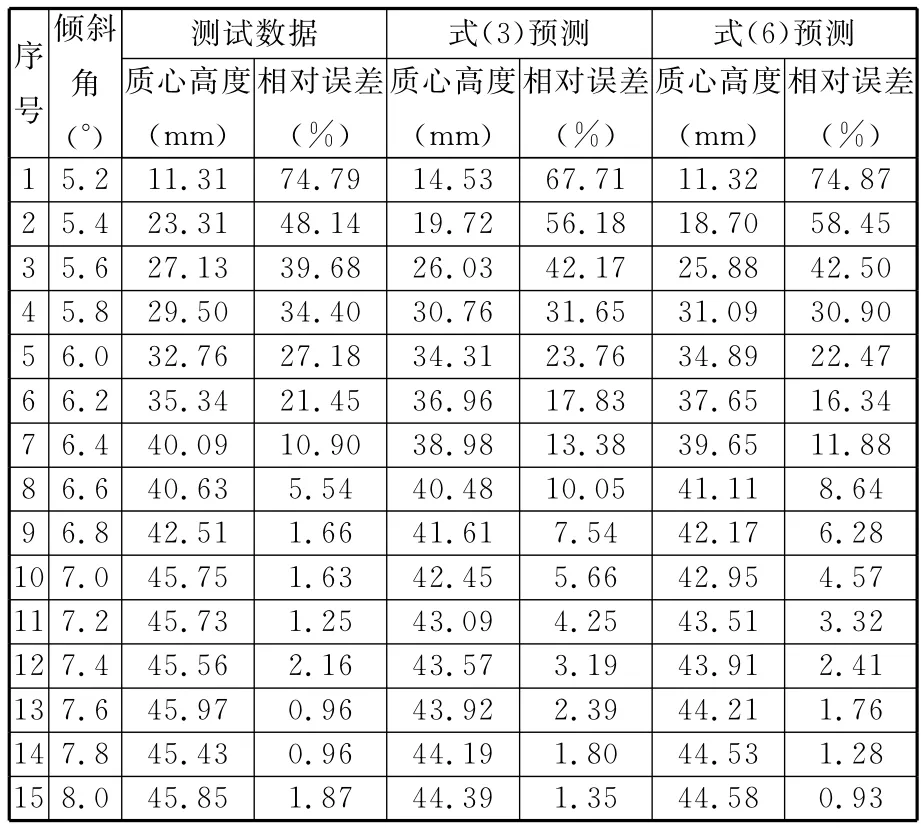
表3 測試數據和改進前后灰色模型預測數據對比

從表3中“式（3）預測”一欄中可以看出，預測模型式（3）與測試數據擬合不是很理想，尤其是在測試角度較大的部分，根據理論與仿真分析所獲得的測試角度越大則測試精度越高的結論，需要對式（3）進行修正，以提高測試數據在大角度位置的擬合程度。

GM（1，1）灰色模型的構建過程就是對測試數據的曲線擬合過程，由于測試系統隨機誤差的存在，測試次數較少，數據的離散性使得擬合曲線不可能通過X（1）序列的任何一個點；同時，在GM（1，1）模型中，采用梯形公式求出定積分的近似值作為背景值z（1）（k＋1），梯形公式存在的誤差將導致模型預測的偏差。利用最小二乘法對初始值（1）和背景值z（1）（k＋1）進行改進，將有利于模型精度的提高，即

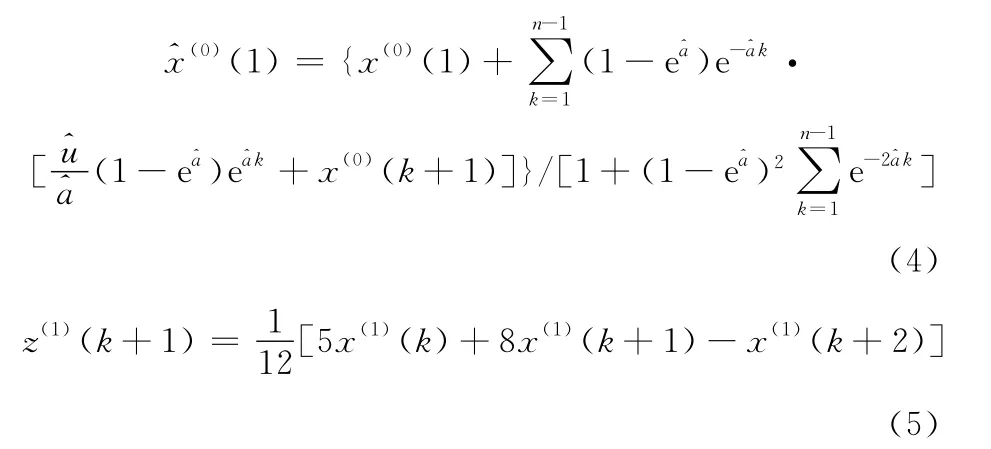
改進后的模型為

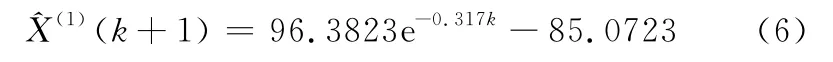
式（6）為基于灰色系統理論的第一級質心位置預測模型，將測試數據代入式（6），計算出當傾斜角為8°時，質心高度為44.58mm，與標準試樣的質心高度相對誤差為0.93%，其精度高于式（3）預測的結果，同時也滿足對第一級預測模型的要求。

從表3可看出改進前后的第一級預測模型與測試數據的擬合程度，改進后的第一級預測模型與原始數據有更為合理的擬合。

4.2 基于BP神經網絡技術的預測模型的建立

根據第一級預測模型可知，在采用三點支撐測試系統進行質心位置測試時，傾斜角越大，測試精度越高。但為了安全起見，一般傾斜角都不大于8°。為進一步提高質心位置預測精度，擬構建以測試角度和第一級預測模型（式（6））的輸出值為輸入元素的基于BP神經網絡的第二級質心位置預測模型。

預測方案：將表3中“式（6）預測”一欄中的前10組數據與相應的測試角度用于神經網絡的訓練。將每5個角度的質心高度數據以及其相應的測試角度作為輸入向量，輸出向量為輸入向量之后的質心高度數據；將表3中“式（6）預測”一欄中的最后5組數據作為測試數據來驗證神經網絡的預測精度。當網絡預測精度達到理想值后，再利用這5組數據進行測試平臺傾斜角大于8°的質心高度參數預測，直到相對誤差收斂為止。

根據預測方案，網絡的輸入向量共10個（5個角度和5個質心位置），目標向量為第6個角度參數時的質心位置值；由于一般預測問題都可以通過單隱層的BP神經網絡實現，根據Kolmogorov定理，確定隱含層神經元數為21個，所構建的BP神經網絡預測模型為10×21×1系統，其中隱含層的神經元傳遞函數采用S型正切函數Tansig，輸出層神經元傳遞函數采用S型對數函數Logsig。在進行參數輸入前，需對輸入元素進行歸一化處理，同樣在完成計算后，所獲得的數據也需進行反歸一化處理。

用MATLAB編寫BP神經網絡程序，并將歸一化后的用于訓練的數據輸入網絡。設定的網絡訓練函數為Trainlm，采用Levenberg－Marquardt算法進行網絡學習。訓練次數為1000，訓練精度為0.001，訓練結果如圖5所示。

將表3中“式（6）預測”一欄中的6～14組數據歸一化后輸入網絡，其預測結果和表3中“式（6）預測”一欄中的11～15組數據進行驗證，結果如圖6所示，最大誤差為0.66%，滿足預測要求。

4.3 質心高度預測與結果分析

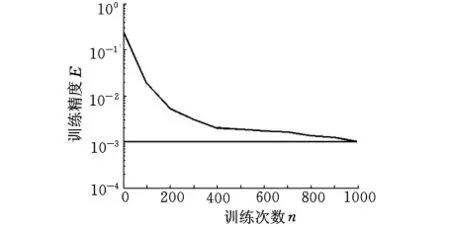
圖5 訓練結果

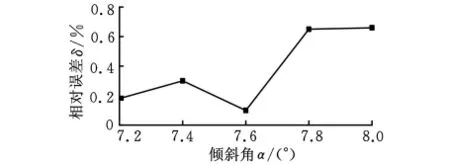
圖6 驗證誤差

將表3中“式（6）預測”一欄中的11～15組數據歸一化后，輸入上述已經完成訓練的網絡，通過預測得出第16組數據，再將表3中“式（6）預測”一欄中的12～15組數據和預測得出的第16組數據一并歸一化后輸入網絡，得出第17組數據，依次循環，直至相對精度收斂為止。預測得到的傾側角度與相對誤差的關系見表4，由表4可知數據在10.4°開始收斂，對應的預測質心高度為44.659mm，與標準試樣的相對誤差為0.759%，滿足測試要求。

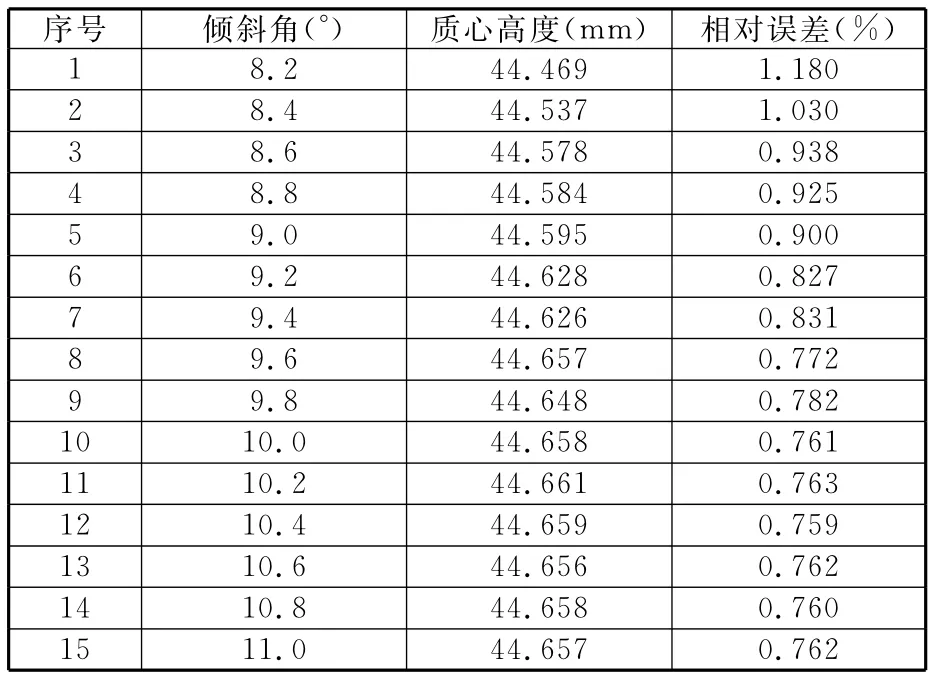
表4 灰色神經網絡質心預測值的相對誤差

5 結語

本文對采用三點支撐質心位置測試系統測量小型作業機質心高度的數據處理方法進行了研究。為解決測試系統中傳感器隨機誤差導致測試數據較大偏離、測試精度降低的難題，結合理論研究和仿真分析的結果，基于灰色BP神經網絡技術，研究了采用GM（1，1）模型與BP神經網絡聯合構建質心高度數據預測模型的方法，并在小型驗證試驗臺上進行驗證。結果證明，根據所建立的預測模型在有限次、小角度條件下，對質心高度測試獲得的數據進行處理可以獲得較高精度的質心高度數據。本文所研究的理論和建模方法可以為小型作業機質心測量系統的高效率、高精度和高安全性的測量提供保證，同樣也可用于大型拖拉機、汽車、航空和航天等其他領域中的各種物體質心高度的測量，同時也為各種智能化測試系統提供了一種減小傳感器隨機誤差對測試精度影響的數據處理方法。

［1]蔣建東，張立彬，胥芳，等.面向大批量定制生產的小型農業作業機客戶需求模型的構建研究［J］.農業工程學報，2005，21（9）：98－102.

［2]張立彬，葉永偉，蔣建東，等.基于可重構模塊化的小型農業作業機方案的設計［J］.農業機械學報，2005，36（4）：78－81.

［3]鐘江，趙章風，喬欣，等.基于三點支撐的質心測量系統及誤差分析［J］.中國機械工程，2010，21（12）：1469－1472.

［4]傅立.灰色系統理論及其應用［M］.北京：科學技術文獻出版社，1992.

［5]楊建鋼.人工神經網絡教程［M］.杭州：浙江大學出版社，2001.

［6]Fabbri A，Molari G.Static Measurement of the Centre of Gravity Height on Narrow－track Agricultural Tractors［J］.Biosystems Engineering，2004，87（3）：299－304.

［7]Kolmogrov A N.On the Representation of Continuous Function of Many Variables by Superposition of Continuous Function of One Variable and Addition［J］.American Math.Society Trans.，1963，28（1）：55－59.

［8]Zhong Luo，Yuan Jingling，Xia Hongxia.A Study on Gray Neural Network Modeling［C］／／Proceedings of the First International Conference on Machine Learning and Cybernetics.Bejing：2002，2021－2023.

［9]鐘珞，白振剛，夏紅霞，等.灰色問題神經網絡建模優化及其應用［J］.計算機工程與應用，2001，37（8）：33－34.

［10]高瑋，馮夏庭.基于灰色－進化神經網絡的滑坡變形預測研究［J］.巖土力學，2004，25（5）：514－517.