對兩個頻率相近成分作頻譜校正的非迭代形式研究

張 強，張 頻，陳奎孚

(1.上海師范大學 建筑工程學院，上海 201418；2.江西農業大學 國土資源與環境學院，南昌 330045；3.中國農業大學 理學院，北京 100083)

對于非密集頻率復雜諧波信號，基于復正弦模型(Complex Sinusoid Model：CSM)的校正技術已經發展得幾近完美［1－6］，有關的綜述參考文獻［7－8］。該方法僅僅利用主瓣附近幾條的離散譜線數據，經過簡單運算就可以得到相當精確的參數。對于頻率密集模型，是否還存在這種不需迭代的校正技術，尚未見文獻給出明確答案。最簡單的頻率密集模型是雙頻率模型(Double-Frequency Model：DFM)。針對這種模型，文獻［9］通過搜索兩個頻率分量在復平面上的方位角將其分離，它需要使用數值法搜索。文獻［9－10］直接用數值方法迭代求解非線性頻率方程，因而兩者算法復雜性和運算量都遠遠超出CSM的簡單校正方法。

本文將探索對于DFM，是否存在類似CSM的顯式校正公式。本文的理論分析表明：DFM加矩形窗情形確實有顯式校正公式；但對其他窗函數，校正公式要么不存在，要么過度復雜，因而不具有實用性。

1 CSM存在簡單校正公式的原因

對周期信號和平穩信號，所使用的窗函數一般均為對稱。仔細研究CSM校正公式的推導過程，可以發現：它之所以簡單是因為常見對稱窗函數w(t)的頻譜W(ω)具有如下的兩個特性。

特性1常見的對稱窗函數的頻譜W(ω)一般可以表示為如下形式：

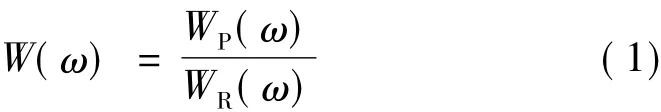
其中：WR(ω)為實有理分式，有的甚至為實多項式；WP(ω)是由三角函數構成的超越實函數。

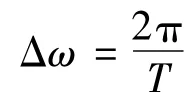
不失一般性，本文僅考慮WP(ω+Δω)=－WP(ω)的情形。

對于單頻復解析信號 xa(t)=A0exp(jφ0+jω0t)加w(t)的傅里葉變換為：

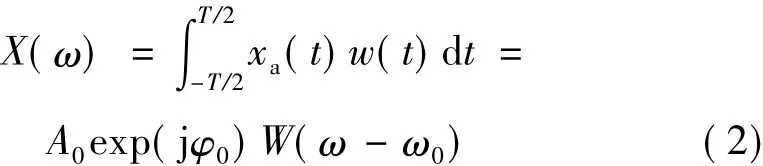
記主瓣內相鄰的兩條FFT譜線ω1和ω2對應的頻譜為X1和 X2，即：

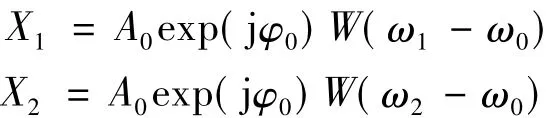
由于FFT的譜線間隔Δω=ω2－ω1=2π/T，因此二者的比值為：

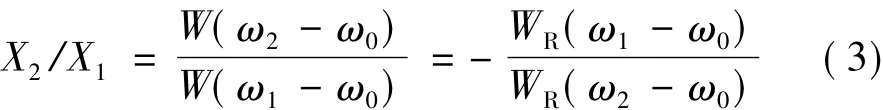
其中利用了特性1和特性2。正因為這兩個特性，X1和X2的超越部分抵消而使得X2/X1僅為ω0的有理函數，進而才有可能建立簡單的校正公式。

比如將漢寧窗 WR(ω)=(ωT/2)［1－(πT/2)2］代入式(2)，立即可以得到它的校正公式。

對于DFM，不再有類似于式(3)的簡單比例關系。但是如果能將兩個所對應頻譜分離，則各自參數應滿足這個比例關系。

2 DFM的頻率方程

記DFM的信號為：

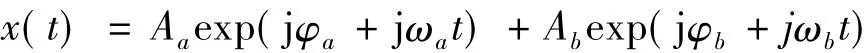
其中的 Aa，φa，ωa，Ab，φb，ωb分別為兩個頻率成分的幅值、相位和頻率參數。根據傅里葉變換的線性性質，有：

考察雙頻率主峰附近的四條連續譜線。記頻率為ω1～ω4，對應的頻譜為 X1～X4，即：

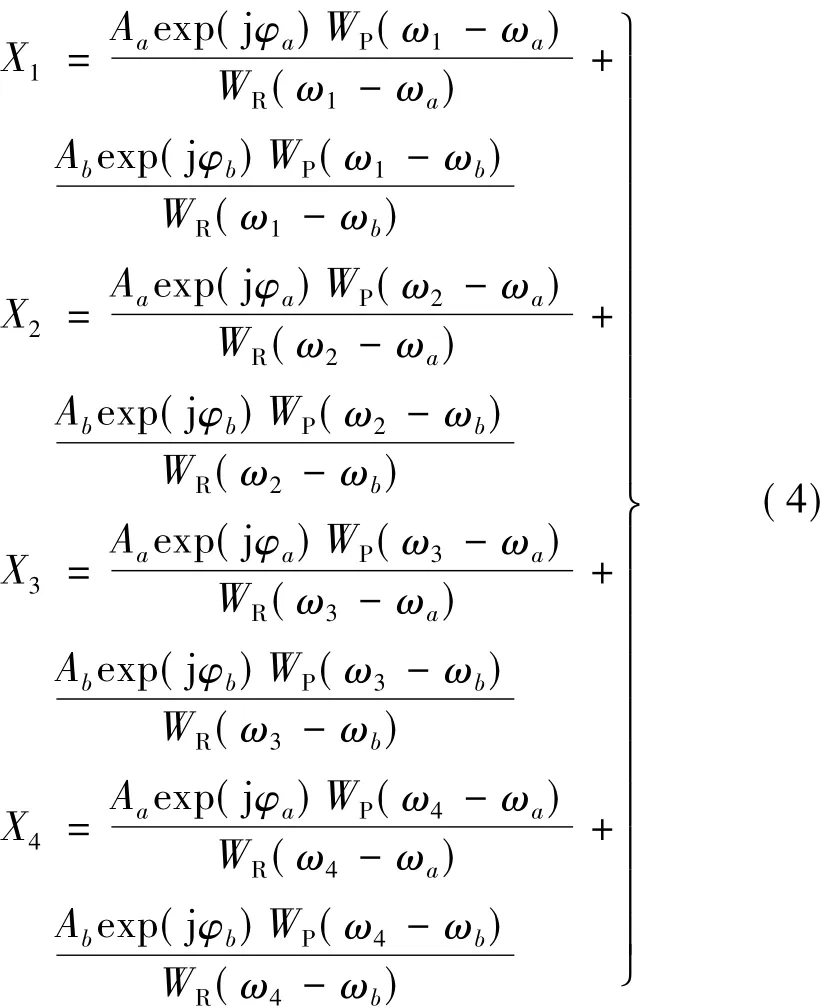
方程組(4)有8個待定參數，但是每個方程都是復方程，虛部和實部各提供一個方程，因此有8個方程。但是本文不直接解這8個方程，而是利用特性2。根據該特性，方程組(4)的每個方程右端兩個分子為：

盡管方程組(4)無超越函數，但也未必能夠得到顯式解。比如高于5次多項式的方程，有所謂的阿貝耳定理，即方程的根不可能用方程系數經過有限次四則運算和開方運算表達出來。退一步，即使有顯式解，若其表達式非常復雜，則實用性也不大。如簡單的三次多項式方程，它的顯式根很復雜。

3 DFM加矩形窗的校正

下面研究DFM加矩形窗簡化情形。

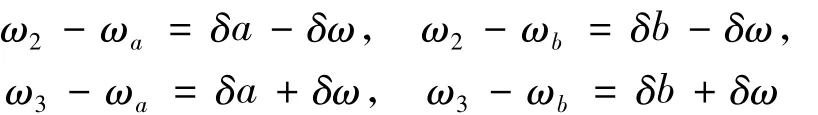
這樣方程組(4)的第2和第3兩式變為：

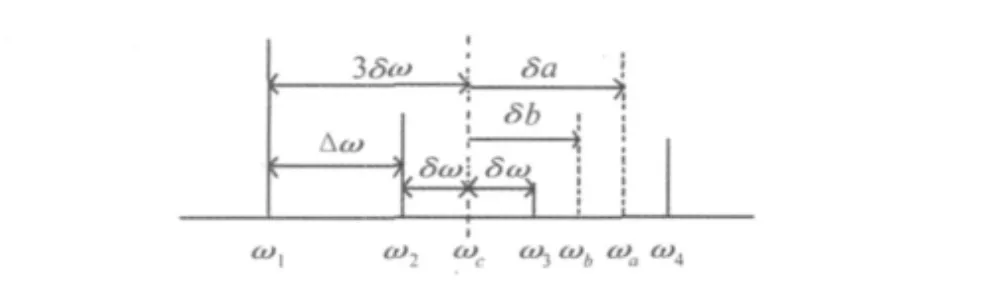
圖1 頻率參數之間的關系Fig.1 The relationship between the frequency variables

不失一般性，取T=2。將WR(ω)=ω代入式(5)，利用克萊姆法則可以解出：

對于方程組(4)的第1和4式，只需將X1→X2，X3→X4，3δω→δω 代入式(6)即有：

將方程(8)的第1式展開得：

將方程(8)第2式作類似展開，然后與式(9)相減，并消去公因式δa－δb得到：

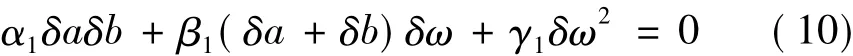
式中：

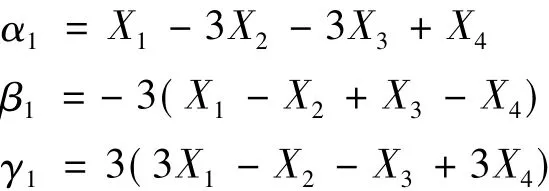
將式(10)的第一項δaδb表示出來：

然后代入式(9)的第1項，經整理可得另外一個方程：

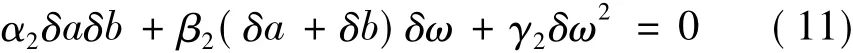
其中：

聯立式(10)和式(11)，可以解出：

其中Δ，Δ1和Δ2是中間變量，具體為：

由式(12)可以看出頻率校正量仍然僅與頻譜比值有關。但是對于DFM，離散譜線在復數平面內不再共線［11］，因此虛部和實部都出現在校正公式上。

由于Δ，Δ1和 Δ2均為復數，因此式(12)中－4Δ1Δ是否大于零并不重要。在理論上δa，δb應該全為實數，但是由于誤差存在，很難保證其虛部為零，通常取其實部作為δa，δb的近似即可。

由圖1的關系，可以得到校正后的頻率：

以上是針對時間零點位于窗函數中心建立的公式。對于常用軟件包的FFT，零點位于窗口最左側。根據傅里葉變換的時移性質，FFT的奇數條譜線將附加一個π相位，而偶數條譜線不變。因而所有推導過程和最終結果應將 －X1→X1，－X3→X3。

由式(12)的推導過程可以看出，如果將矩形窗換成更復雜函數，則無法得到平行于式(10)和(11)的二次多項式方程，因此校正量雖然與頻譜的比值存在確定關系，但是顯式表達式將很復雜或者根本就得不到。

4 考核結果與討論

為了驗證式(12)和式(13)的正確性，以及評價它們的實用性，計算參數取T=2，FFT的長度N=1 024。因此，ΔT=T/N=1/512，Δω =2π/T=π。DFM 信號的兩個成分為：成分1為強幅成分，參數有兩組，即Aa=10，ωa=100.05Δω，φa= π/3 和 Aa=10，ωa=100.55 Δω，φa=π/3，前者接近整周期采樣，后者接近半周期采樣；成分2為弱幅成分，Ab=1，φb=5π/4。為了細致考核校正公式的效果，ωb在一個范圍內取值，即ωb=ωa+ρΔω，其中 ρ=0.3～3Δω。

仿真考核的誤差如圖 2 所示，其中 εω/Δω，εA，εφ分別為校正后的頻率絕對誤差、幅值相對誤差和相位誤差。

圖2 仿真考核的誤差特性Fig.2 The error characteristics of the tested example

由圖2可以看出，強幅成分的參數精度很高，誤差的總趨勢隨兩個頻率的分離而下降，當ρ＞0.5之后，εω只有萬分之幾個 Δω，幅值相對誤差量級不超過10－4，相位誤差也只有零點幾度，且整周期采樣與否對幅值和頻率的精度影響不大(但成分1是否為整周期采樣對成分2的精度影響比較大)。

對影響誤差的各種因素比較發現：對誤差影響最大的因素是FFT的矩形積分法對精確積分接近程度［12］，特別是窗函數兩端權不為零，而數值積分又沒有計入這個值的影響。

在成分1的誤差曲線上標有X的點，該點附近的誤差很大，其原因是式(12)中的Δ→0，因此數值上出現奇異。在校正實施中必須檢查這個值，以確定結果的可靠性。如果不考慮這一點，根據誤差隨頻率差而總體下降的趨勢，式(12)也適用于CSM的頻譜校正。

弱幅成分的參數識別誤差較大，但當ρ=0.5～2(即若兩成分頻率間隔界于 0.5Δω ～2.0Δω)，則頻率誤差不超過0.1Δω，幅值相對誤差低于5%，相位誤差在幾度范圍之內，大體可滿足工程精度的要求。

但是隨ρ繼續增大，弱幅成分的參數誤差趨勢并非繼續降低。這是因為隨ρ增大，弱幅成分對強幅成分主峰附近的頻譜貢獻越小，因而利用強幅成分主峰周圍譜線估計的弱幅信號參數的精度越來越差，尤其是奇點(圖中標有X的點)頻度也加增大。因而對于弱幅成分，如果ρ＞2，不如采用CSM校正公式更為可靠。

弱幅成分的頻率估計奇點往往由Δ=0所造成，但式(13)的Wp(ω2－ωa)也會導致幅值和相位的估計奇點。

5 結論

分析了單頻率模型的頻譜存在簡單校正公式的原因。原因是常用窗函數的譜函數可以分解為超越函數與有理分式的乘積，前者對離散譜線間隔有周期性。利用這個特性很容易建立單頻率模型的加對稱窗的頻譜校正公式。將該特性用于雙頻率模型(DFM)，也可以得到對應的頻率方程，但是其關系非常復雜。除了加矩形窗外，其他窗情形涉及到高于2次的多項式方程，因此顯示校正公式可能不具有實用性或根本不存在。

對于DFM加矩形窗，頻率校正量滿足二次多項式方程，因此可以寫出其顯式解，但是其復雜性遠遠超出單頻率模型的校正公式。采用含幅值差異較大的兩個頻率成分的信號，對這組顯式校正公式進行了考核。結果表明，對于強幅成分，在工程精度內可以認為無誤差，而對弱幅成分，當兩頻率間隔在0.5～2個頻率分辨率范圍之內，誤差在工程精度上可以容忍。如果頻率相距比較大，還是各自采用單頻率模型為宜。

該方法的噪聲特性需要進一步探討。

［1］沈玉娣，劉 雄，趙振毅.機械故障診斷－FORTRAN源程序匯編［M］.西安：西安交通大學出版社，1990.

［2］黃迪山.FFT相位誤差分析及實用校正方法［J］.振動工程學報，1994，7(2)：185－189.

［3］謝 明，丁 康.頻譜分析的校正方法［J］.振動工程學報，1994，7(2)：172－179.

［4］丁 康，謝 明.離散頻譜三點卷積幅值校正法的誤差分析［J］.振動工程學報，1996，9(1)：92－98.

［5］丁 康，鐘舜聰，朱小勇.離散頻譜相位差校正方法研究［J］.振動與沖擊，2001，20(2)：52－55.

［6］朱利民，鐘秉林，黃 仁.離散頻譜多點卷積幅值修正法的理論分析［J］.振動工程學報，1999，12(1)：120－126.

［7］丁 康，張曉飛.頻譜校正理論的發展［J］.振動工程學報，2000，13(1)：14－22.

［8］段虎明，秦樹人，李 寧.離散頻譜的校正方法綜述［J］.振動與沖擊，2007，26(11)：138－144.

［9］謝 明，丁 康.兩個密集頻率成分重疊頻譜的校正法［J］.振動工程學報，1999，12(1)：109－114.

［10］陳奎孚，張森文.利用三條譜線計算頻率緊鄰的兩個成分的參數［J］.振動工程學報，2004，17(2)：153－158.

［11］謝 明，丁 康，莫克斌.頻譜校正時譜線干涉的影響及判定方法［J］.振動工程學報，1998，11(1)：22－28.

［12］陳奎孚，焦群英，高小榕.改善FFT精度的2種算法比較［J］.中國農業大學學報，1996，1(6)：74－79.