關于n長路的（a，b；n）－優美標號

馬鳳敏，吳曉春，張 偉，張慶成

（1.河北工業職業技術學院基礎部，河北 石家莊 050000；2.東北師范大學數學與統計學院，吉林 長春 130024）

1 預備知識

對于一個圖G（V，E），如果對每一個v∈V（G），存在一個非負整數g（v）（稱為頂點v的標號）滿足：（1）max｛g（v）｜v∈V｝＝｜E（G）｜；（2）?u，v∈V，如果u≠v，則g（u）≠g（v）；（3）?e1，e2∈E（G），如果e1≠e2，則g＊（e1）≠g＊（e2），其中g＊（e）＝｜g（u）－g（v）｜，uv＝e（稱為由g導出的邊標號），則稱G為優美圖，稱g為G的一個優美值或優美標號.設Pn是一個n長路，其上的點依次為v0，v1，…，vn，a和b是非負整數，若Pn的優美標號g 滿足g（v0）＝a，g（vn）＝b，則稱g是Pn的一個（a，b；n）－優美標號，記為g（a，b，n），稱Pn是（a，b；n）－優美的.

優美標號的概念是由Golomb在文獻［1］中給出的.由于應用范圍的廣泛性，許多學者做了大量的研究工作，已有詳盡的研究成果［2］.2004年，P.Gvozdjak在文獻［3］中為了解決著名的Oberwolfach問題，提出（a，b；n）－優美猜想：路Pn是（a，b；n）－優美的當且僅當非負整數a，b，n滿足：（1）b－a與n（n＋1）／2有相同的奇偶性；（2）0＜｜b－a｜≤（n＋1）／2；（3）n／2≤a＋b≤3n／2.

該猜想的必要性已由P.Gvozdjak在文獻［3］中給出.關于充分性，文獻［3］對n≤20的情況驗證成立.a＝0的情況，S.M.Lee等人在文獻［4］給出.a＝1，2的情況由文獻［5］解決了.a＝3的情況我們已另文證明.本文則證明了a＝4時，（a，b；n）－優美猜想成立.

為方便我們約定，Z表示整數集，Z［m，k］＝｛x∈Z｜m≤x≤k｝，當k＞m 時，記Z［m，k］＝?.

2 結果及證明

我們首先利用非負整數a，b，n滿足（a，b；n）－優美猜想條件，把n和b進行分類.

引理2.1 當a＝4，非負整數a，b，n滿足（a，b；n）－猜想條件，則

n≥16，b＝（n－7）／2或b＝（n－3）／2或b＝（n＋1）／2或b＝（n＋5）／2或b＝（n＋9）／2.

引理2.2 當a＝4，n為偶數時，該猜想成立.即對滿足猜想條件的b和偶數n，Pn是（4，b；n）－優美的.

證明思路是將部分特殊值具體標出，一般情形對n分情況進行處理.

證明 a＝4.

當n≥16時，把n分成5種情況討論：

情形1 當n≡0（mod 10）.

當n≥40時，我們定義v1，v2，…，v10（3＋m）的優美標號g如下：

（1）當b＝（n－8）／2，m＝n／10－4，我們定義vn－9，vn－8，…，vn＋1的優美標號g如下：

（2）當b＝（n－4）／2，m＝n／10－4，我們定義vn－9，…，vn－8，vn＋1的優美標號g如下：

（3）當b＝n／2，m＝n／10－4，我們定義vn－9，vn－8，…，vn＋1的優美標號g如下：

（4）當b＝（n＋4）／2，m＝n／10－5，我們定義vn－19，vn－18，…，vn＋1的優美標號g如下：

（5）當b＝（n＋8）／2，m＝n／10－4，我們定義vn－9，vn－8，…，vn＋1的優美標號g如下：

情形2 當n≡2（mod 10）.

當n≥42時，我們定義Pn的（4，b；n）－優美標號如下：

（1）頂點v1，v2，…，v10（3＋m）的優美標號g與情形1給定的g 相同.

（2）當b＝（n－8）／2，m＝（n－2）／10－4，我們定義vn－11，vn－10，…，vn＋1的優美標號g如下：

（3）當b＝（n－4）／2，m＝（n－2）／10－4，我們定義vn－11，vn－10，…，vn＋1的優美標號g如下：

（4）當b＝n／2，m＝（n－2）／10－4，我們定義vn－11，vn－10，…，vn＋1的優美標號g如下：

（5）當b＝（n＋4）／2，m＝（n－2）／10－4，我們定義vn－11，vn－10，…，vn＋1的優美標號g如下：

（6）當b＝（n＋8）／2，m＝（n－2）／10－4，我們定義vn－11，vn－10，…，vn＋1的優美標號g如下：

情形3 當n≡4（mod 10）.

當n≥44時，我們定義Pn的（4，b；n）－優美標號如下：

（1）頂點v1，v2，…，v10（3＋m）的優美標號g與情形1給定的g 相同.

（2）當b＝（n－8）／2，m＝（n－4）／10－4，我們定義vn－13，vn－12，…，vn＋1的優美標號g如下：

（3）當b＝（n－4）／2，m＝（n－4）／10－4，我們定義vn－13，vn－12，…，vn＋1的優美標號g如下：

（4）當b＝n／2，m＝（n－4）／10－3，我們定義vn－3，vn－2，…，vn＋1的優美標號g如下：

（5）當b＝（n＋4）／2，m＝（n－4）／10－3，我們定義vn－3，vn－2，…，vn＋1的優美標號g如下：

（6）當b＝（n＋8）／2，m＝（n－4）／10－5，我們定義vn－23，vn－22，…，vn＋1的優美標號g如下：

情形4 當n≡6（mod 10）.

當n≥46時，我們定義Pn的（4，b；n）－優美標號如下：

（1）頂點v1，v2，…，v10（3＋m）的優美標號g與情形1給定的g 相同.

（2）當b＝（n－8）／2，m＝（n－6）／10－4，我們定義vn－15，vn－14，…，vn＋1的優美標號g如下：

（3）當b＝（n－4）／2，m＝（n－6）／10－3，我們定義vn－5，vn－4，…，vn＋1的優美標號g如下：

（4）當b＝n／2，m＝（n－6）／10－4，我們定義vn－15，vn－14，…，vn＋1的優美標號g如下：

（5）當b＝（n＋4）／2，m＝（n－6）／10－3，我們定義vn－5，vn－4，…，vn＋1的優美標號g如下：

（6）當b＝（n＋8）／2，m＝（n－6）／10－3，我們定義vn－5，vn－4，…，vn＋1的優美標號g如下：

情形5 當n≡8（mod 10）.

當n≥38時，我們定義Pn的（4，b；n）－優美標號如下：

（1）頂點v1，v2，…，v10（3＋m）的優美標號g與情形1給定的g 相同.

（2）當b＝（n－8）／2，m＝（n－8）／10－3，我們定義vn－7，vn－6，…，vn＋1的優美標號g如下：

（3）當b＝（n－4）／2，m＝（n－8）／10－3，我們定義vn－7，vn－6，…，vn＋1的優美標號g如下：

（4）當b＝n／2，m＝（n－8）／10－3，我們定義vn－7，vn－6，…，vn＋1的優美標號g如下：

（5）當b＝（n＋4）／2，m＝（n－8）／10－3，我們定義vn－7，vn－6，…，vn＋1的優美標號g如下：

（6）當b＝（n＋8）／2，m＝（n－8）／10－3，我們定義vn－7，vn－6，…，vn＋1的優美標號g如下：

引理2.3 當a＝4，n為奇數時，（a，b；n）－優美猜想成立.即對滿足猜想條件的b和奇數n，Pn是（4，b；n）－優美的.當n≥16，我們分以下5種情形分別討論：

情形1 n≡1（mod 10）.

當n≥41時，我們定義Pn的（4，b；n）－優美標號如下：

（1）頂點v1，v2，…，v10（3＋m）的優美標號g與引理2.2情形1給定的g相同.

（2）當b＝（n－7）／2，m＝（n－1）／10－4，我們定義vn－10，vn－9，…，vn＋1的優美標號g如下：

（3）當b＝（n－3）／2，m＝（n－1）／10－4，我們定義vn－10，vn－9，…，vn＋1的優美標號g如下：

（4）當b＝（n＋1）／2，m＝（n－1）／10－4，我們定義vn－10，vn－9，…，vn＋1的優美標號g如下：

（5）當b＝（n＋5）／2，m＝（n－1）／10－5，我們定義vn－20，vn－19，…，vn＋1的優美標號g如下：

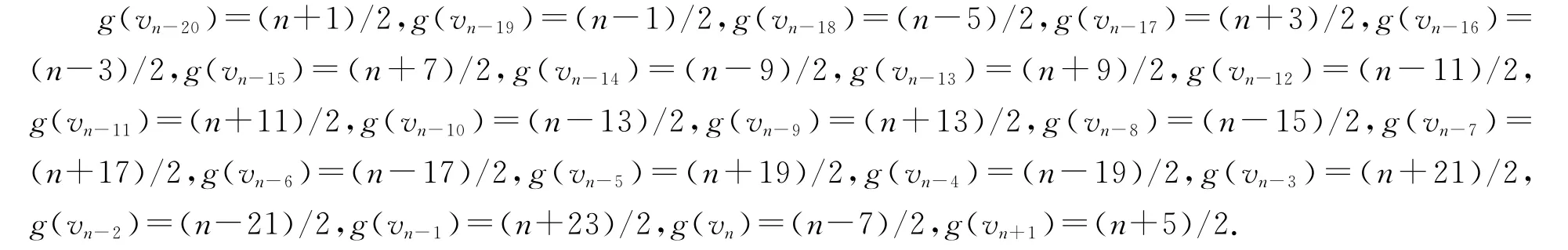
（6）當b＝（n＋9）／2，m＝（n－1）／10－4，我們定義vn－10，vn－9，…，vn＋1的優美標號g如下：

情形2 當n≡3（mod 10）.

當n≥43，我們定義Pn的（4，b；n）－優美標號如下：

（1）頂點v1，v2，…，v10（3＋m）的優美標號g與引理2.2情形1給定的g相同.

（2）當b＝（n－7）／2，m＝（n－3）／10－4，我們定義vn－12，vn－11，…，vn＋1的優美標號g如下：

（3）當b＝（n－3）／2，m＝（n－3）／10－4，我們定義vn－12，vn－11，…，vn＋1的優美標號g如下：

（4）當b＝（n＋1）／2，m＝（n－3）／10－4，我們定義vn－12，vn－11，…，vn＋1的優美標號g如下：

（5）當b＝（n＋5）／2，m＝（n－3）／10－4，我們定義vn－12，vn－11，…，vn＋1的優美標號g如下：

（6）當b＝（n＋9）／2，m＝（n－3）／10－4，我們定義vn－12，vn－11，…，vn＋1的優美標號g如下：

情形3 當n≡5（mod 10）.

當n≥45時，我們定義Pn的（4，b；n）－優美標號如下：

（1）頂點v1，v2，…，v10（3＋m）的優美標號g與引理2.2情形1給定的g相同.

（2）當b＝（n－7）／2，m＝（n－5）／10－4，我們定義vn－14，vn－13，…，vn＋1的優美標號g如下：

（3）當b＝（n－3）／2，m＝（n－5）／10－3，我們定義vn－4，vn－3，…，vn＋1的優美標號g如下：

（4）當b＝（n＋1）／2，m＝（n－5）／10－3，我們定義vn－4，vn－3，…，vn＋1的優美標號g如下：

（5）當b＝（n＋5）／2，m＝（n－5）／10－3，我們定義vn－4，vn－3，…，vn＋1的優美標號g如下：

（6）當b＝（n＋9）／2，m＝（n－5）／10－5，我們定義vn－24，vn－23，…，vn＋1的優美標號g如下：

情形4 當n≡7（mod 10）.

當n≥47，我們定義Pn的（4，b；n）－優美標號如下：

（1）頂點v1，v2，…，v10（3＋m）的優美標號g與引理2.2情形1給定的g相同.

（2）當b＝（n－7）／2，m＝（n－7）／10－3，我們定義vn－6，vn－5，…，vn＋1的優美標號g如下：

（3）當b＝（n－3）／2，m＝（n－7）／10－3，我們定義vn－6，vn－5，…，vn＋1的優美標號g如下：

（4）當b＝（n＋1）／2，m＝（n－7）／10－4，我們定義vn－6，vn－5，…，vn＋1的優美標號g如下：

（5）當b＝（n＋5）／2，m＝（n－7）／10－3，我們定義vn－6，vn－5，…，vn＋1的優美標號g如下：

（6）當b＝（n＋9）／2，m＝（n－7）／10－3，我們定義vn－6，vn－5，…，vn＋1的優美標號g如下：

情形5 當n≡9（mod 10）.

當n≥39，我們定義Pn的（4，b；n）－優美標號如下：

（1）頂點v1，v2，…，v10（3＋m）的優美標號g與引理2.2情形1給定的g相同.

（2）當b＝（n－7）／2，m＝（n－9）／10－3，我們定義vn－8，vn－7，…，vn＋1的優美標號g如下：

（3）當b＝（n－3）／2，m＝（n－9）／10－3，我們定義vn－8，vn－7，…，vn＋1的優美標號g如下：

（4）當b＝（n＋1）／2，m＝（n－9）／10－3，我們定義vn－8，vn－7，…，vn＋1的優美標號g如下：

（5）當b＝（n＋5）／2，m＝（n－9）／10－3，我們定義vn－8，vn－7，…，vn＋1的優美標號g如下：

（6）當b＝（n＋9）／2，m＝（n－9）／10－3，我們定義vn－8，vn－7，…，vn＋1的優美標號g如下：

由引理2.1—2.3可得本文主要結果：

定理2.1 當a＝4時，（a，b；n）－優美猜想成立.即對滿足猜想條件的b，n，Pn（n≥4）是（4，b；n）－優美的.

［1］GOLOMB S W.How to number a graph，in graph theory and computing［M］.New York：Acadmic Press，1972：23－37.

［2］GALLIAN J A.A dynamic survey of graph labeling［J］.The Electronic Journal of Combinarorics，2009（DS6）：1－219.

［3］GVOZDJAK P.On the oberwolfach problem for cycles with multiple lengths［D］.Burnaby：Simon Fraser University，2004.

［4］LEE S M，LAI K Y，WANG Y S.On the graceful permutation graphs conjecture［J］.Congressus Numerantium，1994，103（2）：193－201.

［5］范麗霞，梁志和.關于n長路的（a，b；n）－優美猜想［J］.河北師范大學學報：理學版，2010，34（1）：5－9.