月地轉(zhuǎn)移中途軌道修正分析
尹軍用,汪 備
(上海宇航系統(tǒng)工程研究所,上海201108)
1 引言
2007年10月24 日,中國(guó)第一顆月球探測(cè)衛(wèi)星“嫦娥一號(hào)”成功發(fā)射。嫦娥一號(hào)衛(wèi)星的轉(zhuǎn)移軌道(不包括調(diào)相軌道)飛行時(shí)間是114h,為了克服探測(cè)器飛向月球過(guò)程中軌道位置和速度誤差的逐漸發(fā)散,嫦娥一號(hào)設(shè)計(jì)了三次中途軌道修正:第一次修正在第17h進(jìn)行,最后一次在第90h進(jìn)行,還有一次作為備選,安排在第41h。實(shí)際上,嫦娥一號(hào)衛(wèi)星飛行十分理想,只是在第41h作了唯一的一次中途軌道修正,修正量4.8m/s。
月地轉(zhuǎn)移和地月轉(zhuǎn)移動(dòng)力學(xué)方程類似,月地轉(zhuǎn)移的軌道特性和地月轉(zhuǎn)移的軌道特性存在對(duì)稱性。因此,月地轉(zhuǎn)移軌道同樣存在中途軌道修正的問(wèn)題,如果月地轉(zhuǎn)移的入軌偏差超過(guò)允許值,卻不進(jìn)行中途軌道修正,則難以保證返回器(艙)的落點(diǎn)精度,甚至不能返回地球。
不管是載人登月還是無(wú)人探月,月地轉(zhuǎn)移中途軌道修正都不可或缺。據(jù)目前了解到的資料,只有前蘇聯(lián)的Luna-16月球采樣返回沒(méi)有進(jìn)行中途軌道修正(主要因?yàn)長(zhǎng)una-16返回地球的精度要求較低),其余月球返回探測(cè)器(Luna-20、Luna-24、探測(cè)器5~8號(hào)等)都進(jìn)行了至少一次月地轉(zhuǎn)移中途軌道修正。
在人類載人登月的歷史中,僅有6次成功的載人登月經(jīng)驗(yàn),即“阿波羅”(Apollo)11號(hào)~Apollo17號(hào)(Apollo-13號(hào)除外),Apollo載人飛船在進(jìn)行月地轉(zhuǎn)移時(shí),至少進(jìn)行1次中途軌道修正,見(jiàn)表1。
表1顯示,Apollo載人登月月地轉(zhuǎn)移中途軌道修正一般分兩次,第一次一般在月地加速后15h左右,第二次中途軌道修正在到達(dá)再入點(diǎn)前3h左右。
載人登月軌道和無(wú)人登月軌道的區(qū)別主要有兩點(diǎn):
其一是載人登月軌道轉(zhuǎn)移時(shí)間一般較短,目的是減少乘員和系統(tǒng)對(duì)能源的消耗。Apollo載人登月系列中,任務(wù)時(shí)間最長(zhǎng)的為Apollo17號(hào),約302h,最短的是Apollo11號(hào),約195h。Apollo載人登月飛船地月轉(zhuǎn)移時(shí)間在69h~81h之間,月地轉(zhuǎn)移時(shí)間在59h~72h之間。而無(wú)人登月任務(wù)因?yàn)閷?duì)載人及附加系統(tǒng)的能源的消耗要求稍低,一般時(shí)間較長(zhǎng)。
其二是載人登月的軌道安全性設(shè)計(jì)要求較高。Apollo載人登月飛船在火箭發(fā)射過(guò)程、地月轉(zhuǎn)移過(guò)程(見(jiàn)圖 1)、著月過(guò)程都考慮了安全返回軌道的設(shè)計(jì)(見(jiàn)圖2)。NASA給“阿波羅”登月飛船設(shè)計(jì)了很高的安全標(biāo)準(zhǔn):從火箭起飛開(kāi)始,航天員完成登月任務(wù)的概率為90%,航天員安全返回地球的概率為99.9%(不管是否完成任務(wù)),而無(wú)人登月任務(wù)的軌道則不需要這么高的安全性。
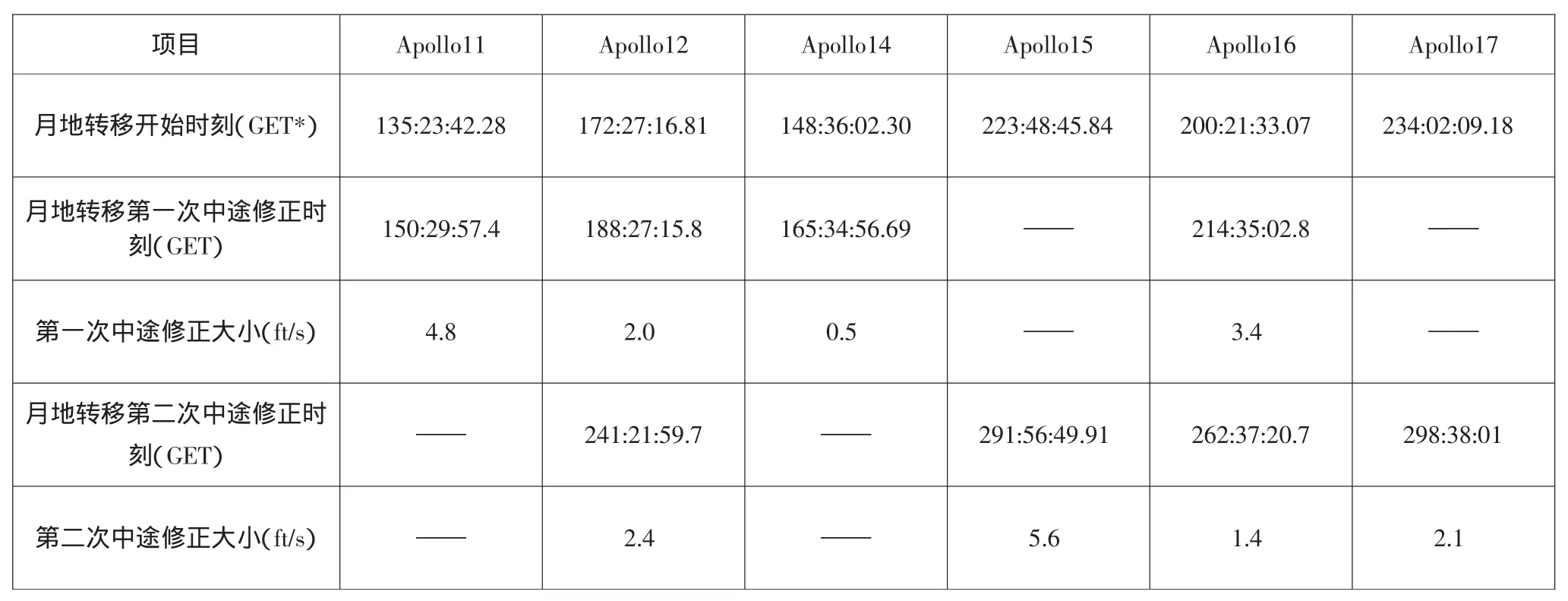
表1 Apollo登月飛船月地轉(zhuǎn)移統(tǒng)計(jì)

圖1 “阿波羅”地月轉(zhuǎn)移過(guò)程的中止軌道

圖2 “阿波羅”著月過(guò)程的中止軌道
Apollo地月/月地轉(zhuǎn)移中途修正的目的有兩類:
一類是修正軌道入軌偏差。由于入軌時(shí)間誤差、控制誤差、導(dǎo)航誤差等因素的影響,Apollo飛船入軌后會(huì)與預(yù)先設(shè)計(jì)的軌道有一定偏差,且到達(dá)月球(或返回地球)的軌道參數(shù)也與期望值不同,必須在中途進(jìn)行軌道修正以滿足到達(dá)月球(或返回地球)的軌道約束。修正軌道入軌偏差的修正量和入軌偏差有關(guān)系。
另外一類修正的目的是改變目標(biāo)軌道。Apollo載人登月軌道的安全性軌道設(shè)計(jì)要求比較高,一般發(fā)射軌道采用自由返回軌道,但是自由返回軌道有一定的局限性,即著月點(diǎn)限定在月球赤道附近,無(wú)法到達(dá)月球高緯度地區(qū),因此,實(shí)際Apollo地月轉(zhuǎn)移軌道常采用混合軌道(見(jiàn)圖 3),即載人飛船一開(kāi)始按照自由返回軌道發(fā)射并進(jìn)入轉(zhuǎn)移軌道后,當(dāng)確信船上儀器工作正常時(shí),飛船將進(jìn)行中途軌道修正,偏離自由返回軌道,進(jìn)入目標(biāo)軌道,使飛船能夠降落在月面設(shè)定著陸點(diǎn)。

圖3 “阿波羅”飛船混合軌道
到目前為止,針對(duì)月球探測(cè)器中途軌道修正的研究主要集中在地月轉(zhuǎn)移中途軌道修正,對(duì)月地轉(zhuǎn)移的中途軌道修正尚未看到公開(kāi)的文獻(xiàn),本文的目的是通過(guò)數(shù)值計(jì)算,對(duì)月地轉(zhuǎn)移的中途修正時(shí)間和修正量進(jìn)行分析,為我國(guó)的月球探測(cè)返回軌道設(shè)計(jì)提供理論依據(jù),其適用范圍可以是無(wú)人登月返回,也可以是載人登月返回。
2 模型的建立
2.1 探測(cè)器的動(dòng)力學(xué)方程
月球探測(cè)器在地-月間飛行過(guò)程中,除了受到中心引力體的萬(wàn)有引力以及發(fā)動(dòng)機(jī)的推力外,還受到其它天體(太陽(yáng)、月球/地球等)的引力攝動(dòng),地球、月球非球形攝動(dòng)、太陽(yáng)光壓攝動(dòng)以及大氣阻力等攝動(dòng)作用,在進(jìn)行探月軌道設(shè)計(jì)時(shí)必須考慮這些攝動(dòng)的影響。而對(duì)于探測(cè)器受到的其它的攝動(dòng),比如木星、金星和火星的第三體攝動(dòng)、地球潮汐攝動(dòng)、地球扁率的間接攝動(dòng)、相對(duì)論效應(yīng)攝動(dòng)等,由于其對(duì)探測(cè)器飛行軌道影響較小,在進(jìn)行探測(cè)器軌道設(shè)計(jì)時(shí),可以忽略不計(jì)。
月球探測(cè)器在地心天球坐標(biāo)系中的動(dòng)力學(xué)方程為:
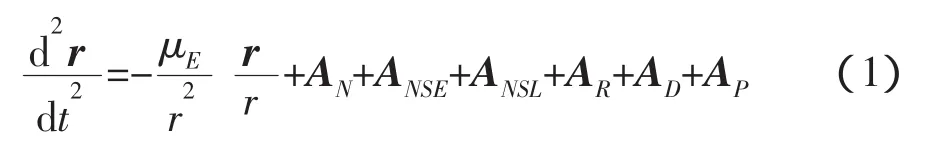
式中,右端第一項(xiàng)為地球的中心引力,其余項(xiàng)為:AN:N體引力攝動(dòng)加速度;ANSE:地球非球形引力攝動(dòng)加速度;AP:推力加速度;ANSL:月球非球形引力攝動(dòng)加速度;AR:光壓攝動(dòng)加速度;AD:大氣阻力攝動(dòng)加速度。
本文中,探測(cè)器的動(dòng)力學(xué)方程主要考慮第三體引力—太陽(yáng)和月球的影響,別的天體攝動(dòng)因素因其量級(jí)較小,暫不考慮。
2.2 地月/月地轉(zhuǎn)移軌道的解法
2.2.1 微分修正法
為簡(jiǎn)單起見(jiàn),僅考慮地球、月球和太陽(yáng)的引力作用,則月球探測(cè)器的軌道動(dòng)力學(xué)方程可以表示為:

若記,則上述二次方程可以改寫為一次方程:


對(duì)方程(4)做變分,得

其中,A(t)=Df(u(t))為f(u)的Jacobian矩陣。
又變分方程(5)具有如下形式的解:
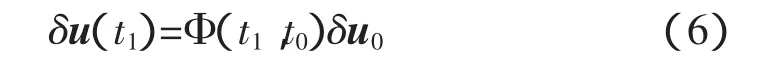

因此,給定初始條件u(t0)=u0,Φ(t0,t0)=I6,通過(guò)

即可解出狀態(tài)轉(zhuǎn)移矩陣 Φ(t,t0)。
2.2.2 地月轉(zhuǎn)移軌道的解法

令
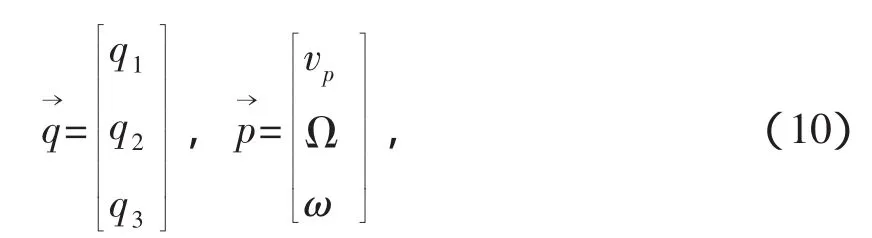
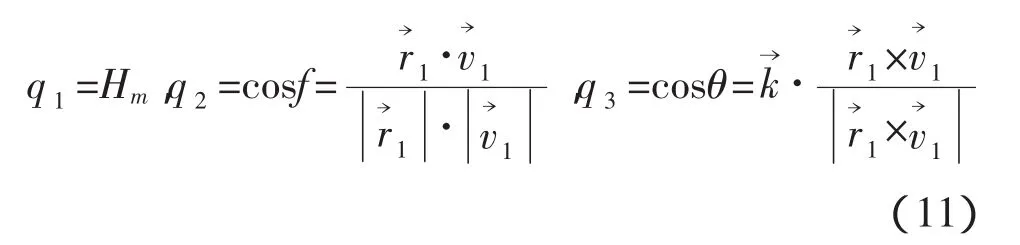
其中,Ω為升交點(diǎn)赤經(jīng),ω為近地點(diǎn)幅角,vp是近地點(diǎn)的速度,Hm為近月點(diǎn)高度,是Z方向的單位矢量。地月轉(zhuǎn)移初始狀態(tài)與終端狀態(tài)之間有著確定的關(guān)系,如下

忽略二階項(xiàng),則兩狀態(tài)的偏差之間的關(guān)系可以用線性近似表示為

利用這一關(guān)系,在一個(gè)合適的初值基礎(chǔ)上,通過(guò)若干次迭代就可以求出十分精確的數(shù)值解。這里的問(wèn)題是,上述偏導(dǎo)數(shù)的分析表達(dá)式無(wú)法給出,但可通過(guò)數(shù)值求出,如下


則,

2.2.3 逆向積分法
在進(jìn)行月地轉(zhuǎn)移軌道計(jì)算時(shí),按照地月轉(zhuǎn)移的思路,初始位置在環(huán)月軌道,末端位置在地球大氣層附近,分別給出兩端的約束條件,可以應(yīng)用微分修正法計(jì)算月地轉(zhuǎn)移軌道。一般的,為了計(jì)算月地轉(zhuǎn)移軌道的方便,可以根據(jù)地月和月地軌道計(jì)算的對(duì)稱性,根據(jù)逆向積分,將月地轉(zhuǎn)移軌道從再入點(diǎn)積分至月球停泊軌道,計(jì)算方法和計(jì)算過(guò)程和計(jì)算地月轉(zhuǎn)移軌道類似,僅僅需要將積分時(shí)間由正變?yōu)樨?fù)。
3 環(huán)月軌道參數(shù)誤差對(duì)再入點(diǎn)偏差的影響
探測(cè)器在月地轉(zhuǎn)移過(guò)程中,對(duì)于不同的月地轉(zhuǎn)移軌道,地—月系統(tǒng)對(duì)探測(cè)器初始入軌誤差都會(huì)逐漸放大,且對(duì)不同軌道的影響會(huì)有所不同。但是,由于整個(gè)轉(zhuǎn)移過(guò)程中的動(dòng)力學(xué)方程完全一致,且都是從月球附近轉(zhuǎn)移到地球附近,雖然其初始參數(shù)和末端參數(shù)不同,但是整個(gè)發(fā)散的量級(jí)是相同的,中途軌道修正的能量也是和初始軌道偏差成正比的。
給定2016年10月10日0時(shí)42分54秒從月球停泊軌道出發(fā)的一條軌道,出發(fā)點(diǎn)在月心慣性系下的參數(shù)為aM=Rm+200km、e=0、i=139.2°、Ω=176.7°、ω=231.9°、f=0°,對(duì)應(yīng)Vp=2459.85m/s。該月地轉(zhuǎn)移軌道轉(zhuǎn)移時(shí)間72h,到達(dá)再入點(diǎn)時(shí)間為2016年10月13日0時(shí)42分54秒,再入點(diǎn)經(jīng)度為57.191deg、再入點(diǎn)緯度為30.433deg。
下面分別研究環(huán)月軌道參數(shù)的偏差對(duì)再入點(diǎn)的影響,方法是對(duì)環(huán)月軌道參數(shù)進(jìn)行拉偏,其中月地轉(zhuǎn)移時(shí)間為從月地加速點(diǎn)至再入點(diǎn)的時(shí)刻間隔,再入點(diǎn)的偏差是在地固系下實(shí)際再入點(diǎn)和期望再入點(diǎn)的直線距離,各種參數(shù)對(duì)再入點(diǎn)的影響見(jiàn)表2~表7。

表2 初始速度偏差對(duì)再入點(diǎn)的影響

表3 初始近月點(diǎn)高度偏差對(duì)再入點(diǎn)的影響

表4 初始軌道傾角偏差對(duì)再入點(diǎn)的影響

表5 初始真近點(diǎn)角偏差對(duì)再入點(diǎn)的影響
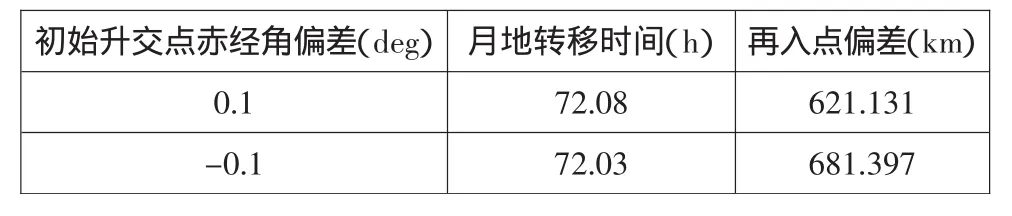
表6 初始升交點(diǎn)赤經(jīng)偏差對(duì)再入點(diǎn)的影響

表7 初始近地點(diǎn)幅角偏差對(duì)再入點(diǎn)的影響
由表2~表7可知,環(huán)月軌道參數(shù)偏差對(duì)再入點(diǎn)的位置影響很大,在沒(méi)有中途軌道修正的情況下,初始速度偏差0.1m/s,再入點(diǎn)位置偏差200km量級(jí);初始近月點(diǎn)高度偏差0.5km,再入點(diǎn)位置偏差在500km量級(jí);初始軌道傾角和真近點(diǎn)角偏差0.1deg,再入點(diǎn)位置偏差在100km量級(jí);初始升交點(diǎn)赤經(jīng)和近地點(diǎn)幅角偏差0.1deg,再入點(diǎn)偏差在600km量級(jí)。
表2~表7說(shuō)明,如果要完成月地轉(zhuǎn)移任務(wù),將返回器返回至預(yù)定的著陸場(chǎng),需要進(jìn)行中途軌道修正。
4 月地轉(zhuǎn)移第一次中途軌道修正的時(shí)間分析
基于前面的調(diào)研分析,本文不加論證的給定月地轉(zhuǎn)移中途軌道修正次數(shù)為2次。
假定速度有1m/s的誤差,在探測(cè)器進(jìn)入月地轉(zhuǎn)移軌道后不同的時(shí)刻(2~71h)進(jìn)行修正,修正脈沖與修正時(shí)刻的關(guān)系見(jiàn)圖4~圖5。
由圖4~圖5可以看出,在進(jìn)入月地轉(zhuǎn)移軌道的初始幾十個(gè)小時(shí)內(nèi),修正時(shí)刻越早,需要的速度修正脈沖越小,但修正量變化緩慢。在到達(dá)再入點(diǎn)的前6個(gè)小時(shí)內(nèi),速度修正脈沖變化比較劇烈,從約50m/s增大到約500m/s,誤差隨著探測(cè)器運(yùn)行時(shí)間的增大逐漸放大,因此,從節(jié)省能量的角度,月地轉(zhuǎn)移第一次中途修正時(shí)間越早越好。根據(jù)由圖4~圖5,速度方向1m/s的速度殘差被放大到10m/s(10倍)需要約50h,放大到 5m/s(5 倍)需要 40h,放大到 2.5m/s(2.5倍)需要20h,因此,建議月地轉(zhuǎn)移第一次中途修正在月地加速后40h之前,此時(shí)誤差放大的量級(jí)在初始速度偏差的5倍范圍內(nèi)。

圖4 第1~60h修正對(duì)應(yīng)的修正脈沖曲線
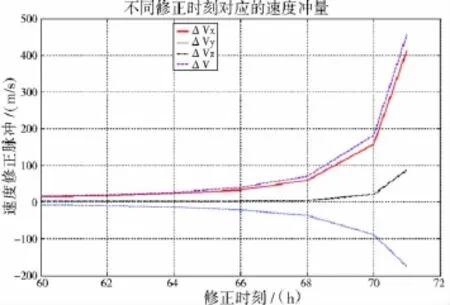
圖5 第60~71h修正對(duì)應(yīng)的修正脈沖曲線
另一方面,如果第一次修正時(shí)刻太早,則殘余誤差會(huì)更多的被放大,會(huì)加重以后的修正任務(wù);另外,進(jìn)入月地轉(zhuǎn)移軌道后,地面對(duì)探測(cè)器的跟蹤定軌還需要一段時(shí)間,一般在月地轉(zhuǎn)移加速12h以后比較合適。
因此,在沒(méi)有對(duì)誤差放大量級(jí)的具體約束條件下,粗定月地轉(zhuǎn)移第一次中途修正在12h~40h之間,后續(xù)仿真暫定為20h。
5 環(huán)月軌道參數(shù)對(duì)中途軌道修正量的影響
當(dāng)探測(cè)器進(jìn)入月地轉(zhuǎn)移軌道的狀態(tài)相對(duì)于標(biāo)稱狀態(tài)有偏差時(shí),在修正時(shí)刻(本文在入軌后20h修正)給探測(cè)器施加一個(gè)速度脈沖,使其到達(dá)再入點(diǎn)的狀態(tài)滿足預(yù)定條件,以下討論速度修正脈沖的大小與環(huán)月軌道參數(shù)誤差量的關(guān)系。
近地點(diǎn)高度的誤差對(duì)軌道的影響比較明顯,見(jiàn)圖6,修正量和誤差量成正比。近地點(diǎn)高度1km的誤差,需要1.8m/s的速度增量修正。
升交點(diǎn)赤經(jīng)的誤差對(duì)軌道的影響見(jiàn)圖 7,修正量和誤差量成正比。升交點(diǎn)赤經(jīng)0.1deg的誤差,需要2.7m/s的速度增量修正。
近月點(diǎn)幅角的誤差對(duì)軌道的影響見(jiàn)圖8,修正量和誤差量成正比。近月點(diǎn)幅角0.1deg的誤差,需要2.5m/s的速度增量修正。
月地加速時(shí)間的誤差對(duì)軌道的影響見(jiàn)圖9,修正量和誤差量成正比。月地加速時(shí)間1min的誤差,需要0.3m/s的速度增量修正。
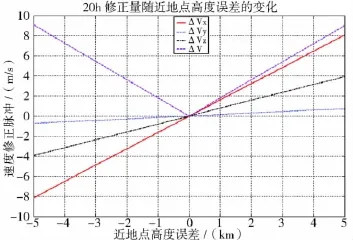
圖6 修正脈沖隨近地點(diǎn)高度誤差的變化曲線

圖7 修正脈沖隨升交點(diǎn)赤經(jīng)誤差的變化曲線
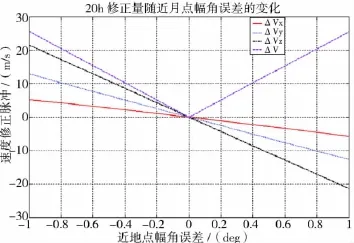
圖8 修正脈沖隨近月點(diǎn)幅角誤差的變化曲線
圖6~圖9顯示,偏差量和修正量有近似線性的的關(guān)系,20h誤差修正量可根據(jù)實(shí)際偏差量近似的估計(jì)出來(lái)。
6 月地轉(zhuǎn)移第二次中途軌道修正的時(shí)間分析
第一次中途修正后,速度方向上仍然會(huì)存在一定的殘余誤差,以1m/s的殘余誤差分析,分析三方向速度殘余誤差對(duì)落點(diǎn)的影響,即在第20h以后的軌道上的某一時(shí)刻,速度拉偏1m/s,計(jì)算拉偏前后的軌道到達(dá)再入點(diǎn)的偏差,見(jiàn)圖10。
從圖 10可知,第二次中途修正(最后一次)時(shí)間越早,其速度殘差對(duì)落點(diǎn)偏差的影響越大。如果從月地轉(zhuǎn)移第20h進(jìn)行修正,三方向1m/s的速度偏差會(huì)分別造成再入點(diǎn)約800km、750km和60km的偏差;如果在再入前1h進(jìn)行修正,1m/s的速度偏差會(huì)造成三方向造成6km、4km和2km的位置偏差。因此,從落點(diǎn)精度的保證來(lái)說(shuō),第二次中途修正越晚越好。

圖9 修正脈沖隨發(fā)射時(shí)間誤差的變化曲線
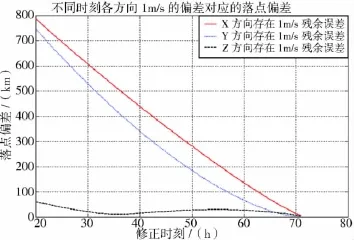
圖10 不同時(shí)刻各方向1m/s的偏差對(duì)再入點(diǎn)的影響
同樣從誤差發(fā)散的角度,第一次中途修正帶來(lái)一定的殘余誤差,第二次中途修正越晚所需要的修正量越大,這點(diǎn)從圖4~圖5可以證明,而且特別明顯的是,速度殘差的發(fā)散在到達(dá)地球前3h劇烈的增大。因此,從節(jié)約能量的角度來(lái)說(shuō),第二次中途修正越早越好,特別是在到達(dá)地球前3h之前的時(shí)刻修正。
一般的,月地轉(zhuǎn)移以保證落點(diǎn)精度為首要任務(wù),但是仍需避免在速度殘差發(fā)散劇烈的階段進(jìn)行修正,因此,建議在再入前3h左右施加第二次中途修正,這也是Apollo飛船選擇再入前3h左右進(jìn)行中途修正的原因。
7 結(jié)論
本文對(duì)月地轉(zhuǎn)移中途軌道修正進(jìn)行了研究,通過(guò)建立探測(cè)器在地—月系統(tǒng)的動(dòng)力學(xué)模型,簡(jiǎn)要分析了初始入軌誤差對(duì)再入點(diǎn)偏差的影響。本文還利用地月/月地轉(zhuǎn)移的中途軌道修正模型和微分修正算法,分析了在存在環(huán)月軌道偏差的條件下,月地轉(zhuǎn)移軌道誤差隨月地轉(zhuǎn)移時(shí)間的發(fā)散過(guò)程,給出初始偏差發(fā)散2.5倍、5倍和10倍大約所經(jīng)歷的時(shí)間。
本文分析第二次中途軌道修正的方法和分析第一次中途軌道修正的方法類似,同樣是分析第一次修正后的殘余誤差在月地轉(zhuǎn)移軌道上的發(fā)散過(guò)程,對(duì)再入點(diǎn)的偏差進(jìn)行分析,該分析可以解釋Apollo載人飛船第二次中途軌道修正的時(shí)間選擇。
受篇幅所限,本文僅僅對(duì)由于入軌誤差的影響而進(jìn)行月地轉(zhuǎn)移中途軌道修正的一類情況進(jìn)行了簡(jiǎn)要的分析,對(duì)于改變目標(biāo)軌道的一類中途軌道修正沒(méi)有研究,這一類的問(wèn)題與自由返回軌道和混合軌道的設(shè)計(jì)關(guān)系密切,需要結(jié)合實(shí)際的載人登月任務(wù)進(jìn)行設(shè)計(jì)。◇
[1]楊維廉,周文艷.嫦娥一號(hào)月球探測(cè)衛(wèi)星軌道設(shè)計(jì)[J].航天器工程,2007,16(8):16-24.
[2]周文艷,楊維廉.月球探測(cè)器轉(zhuǎn)移軌道的中途修正[J].宇航學(xué)報(bào),2004,25(1):89-92.
[3]楊維廉,周文艷.嫦娥一號(hào)衛(wèi)星地月轉(zhuǎn)移軌道中途修正分析[J].空間控制技術(shù)與應(yīng)用,2008,34(6):3-7.
[4]Manned Spacecraft Center.Apollo 11 Mission Report.MSC-00171.
[5] Holley,M.D.,Swingle,W.L.,et al.:Apollo Experience Report-Guidance and Control Systems:Primary Guidance,Navigation,and Control System Development.NASA TN D-8227,1976.

