具有負泊松比效應蜂窩材料的面內沖擊動力學性能＊

張新春，劉 穎，李 娜

（1.華北電力大學機械工程系，河北 保定 071003；2.北京交通大學土建學院力學系，北京 100044）

由于具有獨特的力學性能和可設計性強等優點，具有負泊松比效應多胞材料將成為航空航天、汽車、鐵路和軍事等工程領域不可缺少的材料之一，已引起了廣泛關注［1－8］。多胞材料具有負泊松比現象的一種合理解釋是材料具有內凹的胞元結構（即胞元擴張角θ小于零），研究較多的是六邊形蜂窩及其相應的內凹結構（見圖1）。多胞材料內凹微結構的存在，使它具有一些與實體材料不同的特殊性能。尤其在沖擊荷載作用下，胞元微拓撲結構的改變對材料局部動態應力演化過程的影響更加顯著。因此，如何建立內凹微拓撲結構參數與多胞材料動力學響應間的關系，也是具有負泊松比效應多胞材料力學性能研究的重要目標之一。

具有負泊松比效應多胞材料最早由R.S.Lakes［2］制備，他通過對聚合物泡沫的三軸壓縮和熱處理，制備了具有內凹胞體結構的材料。目前已經有了解釋該現象的多種力學模型［3－8］，并有對這種結構性能進行的大量研究。例如，盧子興等［3］基于旋轉機制，提出了具有負泊松比效應的二維多胞材料力學模型，并預測了模型的泊松比及剛度系數與胞元擴張角之間的關系；J.B.Choi等［4］對內凹泡沫夾芯材料的楊氏模量進行了預測，指出具有負泊松比效應泡沫材料的力學性能與胞元微拓撲結構的改變（由外凸到內凹）有關；D.W.Overaker等［5］研究了微拓撲性和胞元擴張角對六邊形蜂窩材料彈性性能的影響；H.Wan等［6］討論了胞元幾何參數對內凹蜂窩結構泊松比的影響，指出該結構的泊松比隨著應變的改變而變化；J.N.Grima等［7］對泡沫材料中的拉脹特性進行了研究，并提出了一種新的解釋；E.J.Horrigan等［8］使用兩種不同的優化工具，對具有負泊松比效應隨機蜂窩結構的力學性能進行了優化。可見，對具有負泊松比效應多胞材料的大量研究已經展開，但主要集中于靜力學特性的討論。與靜態及準靜態壓縮不同，在沖擊載荷作用下，結構和慣性效應將主要影響材料的動態響應特性。如何建立胞元微拓撲結構參數與材料宏觀動力學性能間關系，也是具有負泊松比效應多胞材料力學特性描述中的一個重要問題。胞元內凹微拓撲結構的變化引起材料中豐富的動力學演化特性還有待于進一步澄清。

本文中，以內凹六邊形蜂窩為研究對象，討論胞元擴張角和沖擊速度對蜂窩材料面內沖擊性能和能量吸收機理的影響，以期建立具有負泊松比效應多胞材料的宏觀動力學響應與胞元擴張角和沖擊速度間的內在關聯。

1 計算模型

1.1 有限元模型

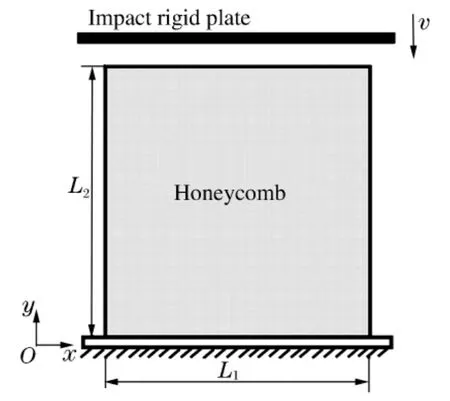
圖2 蜂窩材料的沖擊加載示意圖Fig.2 Diagrammatic sketch for honeycombs under in－plane impact

面內沖擊作用下蜂窩材料的計算模型如圖2所示。試件分別由具有相同壁長和壁厚、但不同擴張角θ（擴張角的定義與文獻［1］完全相同）的內凹六邊形胞元所填充（見圖3）。在本文的討論中，胞元擴張角控制在0～－30°。需要指出的是，當胞元擴張角θ＝－30°時，試件變為規則三角形結構，不屬于本文的研究范疇。基體材料為金屬鋁，采用理想彈塑性模型，楊氏模量Es＝69GPa，泊松比μ＝0.33，屈服應力σys＝76MPa，基體材料的密度ρs＝2.698t／m3。采用顯式動力學軟件LS－DYNA進行動力學特性模擬［9］，計算中使用Shell 163殼單元（4節點四邊形殼單元）進行離散，每條棱邊單元數為6（見圖4）。為了保證收斂，沿厚度方向取五個積分點。對于變形過程中可能的接觸，采用單面自動接觸算法。另外，剛性板表面與蜂窩試件的外表面均視為光滑，兩者接觸無摩擦。采用與文獻［10－11］相同的邊界條件，即當剛性板沿y方向沖擊蜂窩試件時，試件的底端固定，左右兩側自由。另外，為保證變形的平面應變狀態，試件中所有節點面外位移均被限制。模型的面外（沿z方向）厚度b＝1mm。

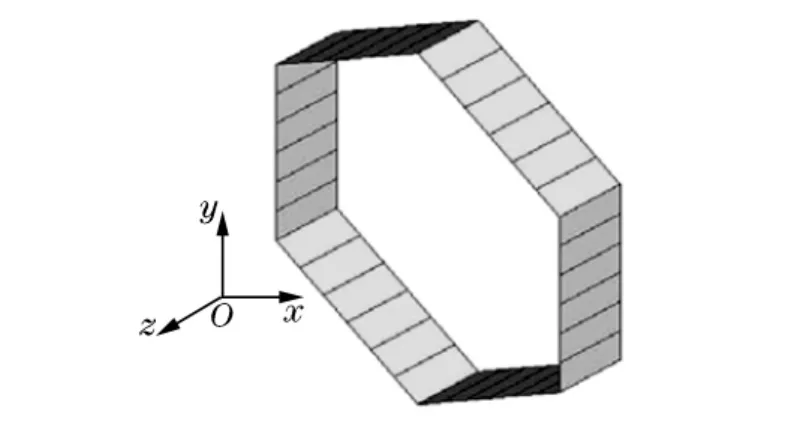
圖4 規則蜂窩結構的網格劃分Fig.4 Mesh division of a regular honeycomb

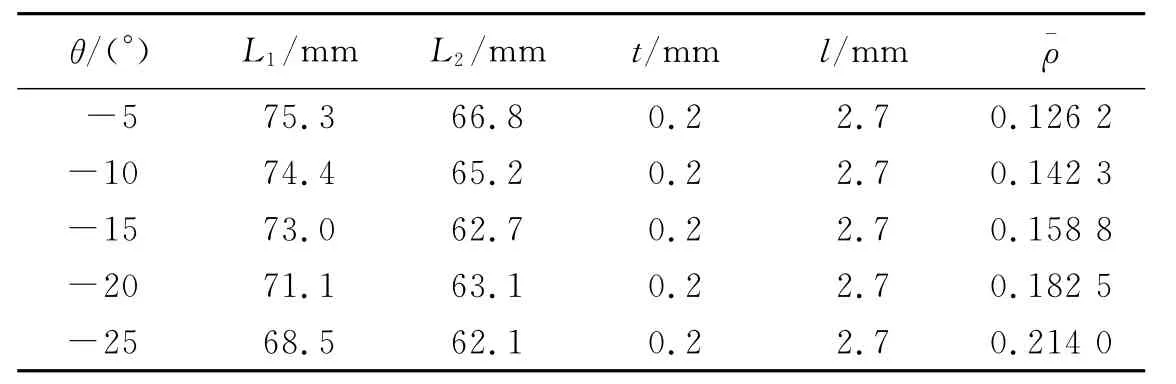
表1 具有負泊松比效應蜂窩材料的性能參數Table1 Characteristic parameters for honeycombs with negative Poisson’s ratio effects

具有負泊松比效應蜂窩材料的相對密度可表示為

式中：ρ＊是蜂窩材料的密度，li是第i個胞壁的長度，ti為相應胞壁的厚度，L1、L2分別是整個試件的寬度和高度。根據方程（1），不同胞元擴張角蜂窩結構的性能參數見表1。

1.2 模型可靠性分析

為了驗證有限元模型的可靠性，建立與文獻［10］完全相同的計算模型，討論規則六邊形蜂窩材料的面內動態響應特性。圖5中給出了剛性板沖擊速度v＝7m／s時，六邊形蜂窩在y方向的沖擊變形特性。由圖可見，在基體材料性能、邊界條件和加載條件完全相同的條件下，計算結果與文獻［10］中面內變形模式基本吻合，證明了該模型的可靠性。

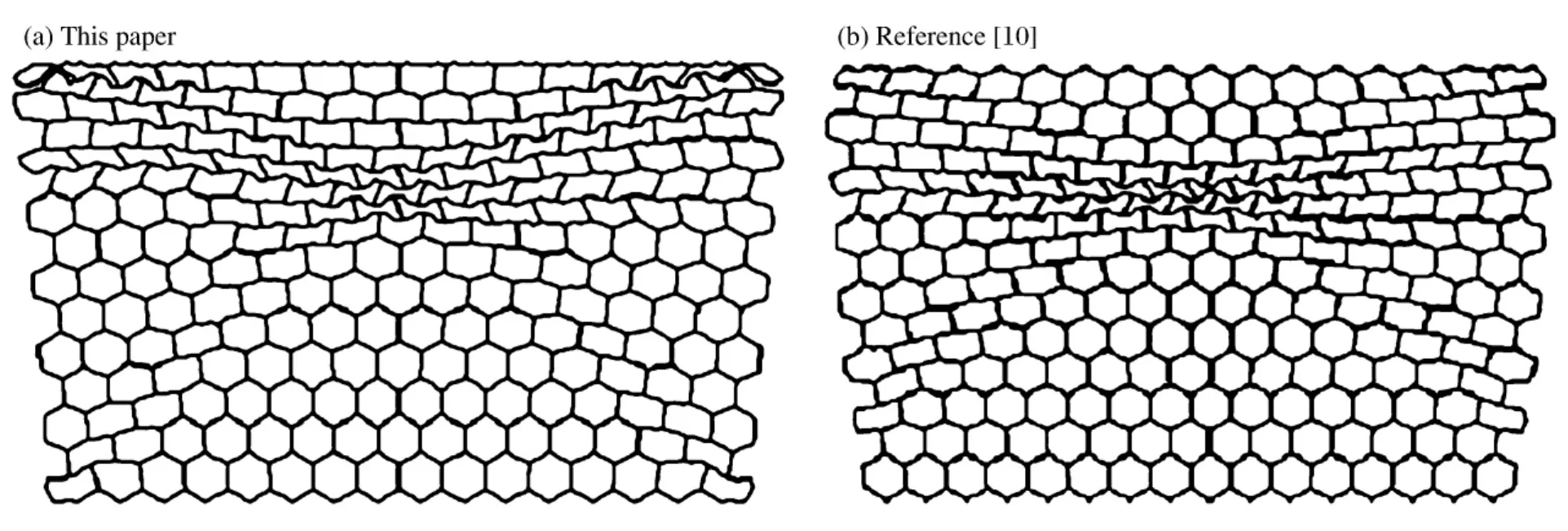
圖5 規則六邊形蜂窩沿y方向的面內變形模式（v＝7m／s）Fig.5 In－plane crushing deformation of regular hexagonal honeycomb in the ydirection

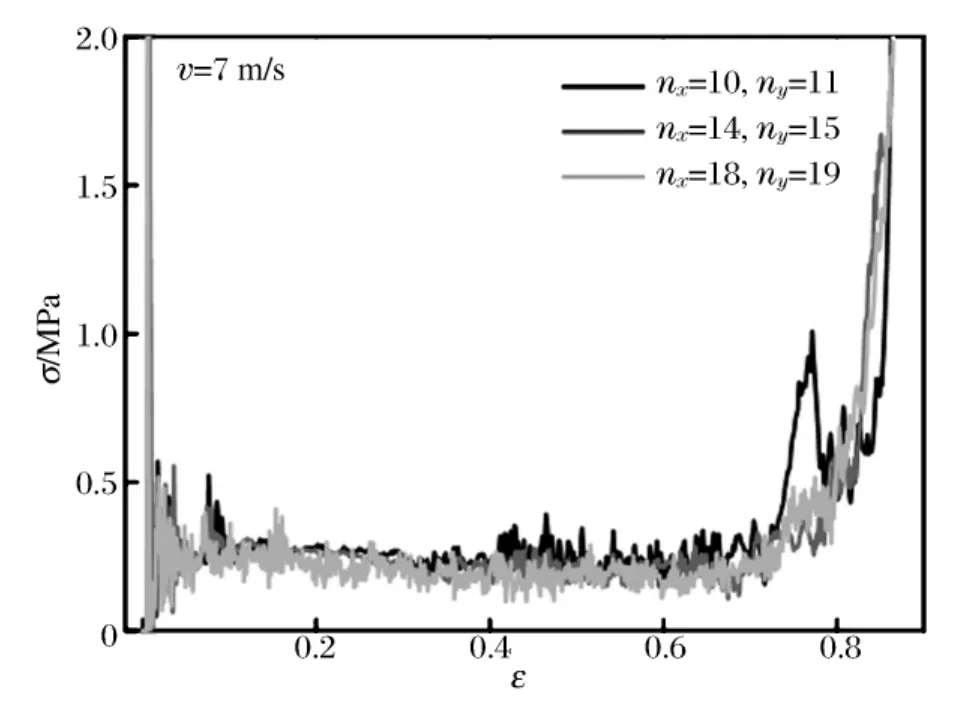
圖6 規則蜂窩材料的動力響應Fig.6 Dynamic response of regular honeycomb

此外，對于蜂窩材料面內動力學特性的模擬，胞元填充數目對模擬結果也有一定的影響。如何有效地捕捉它的態變形特性并保證計算效率，在動態沖擊問題的模擬中十分重要。圖6中討論了剛性板的沖擊速度v＝7m／s時，胞元填充數目對六邊形蜂窩面內動力響應特性的影響。圖中名義應力σ為剛性板作用在試件上的壓縮反力F與初始橫截面面積A 的比值，σ＝F／L1b，名義應變ε為試件沿y方向的相對壓縮量，ε＝δ／L2，δ為沖擊方向剛性板的壓縮位移。研究表明，在x、y方向內填充胞元的數目nx、ny超過10時，動態響應趨于穩定。

在對規則六邊形蜂窩材料研究的基礎上，本文中將系統地討論具有負泊松比效應蜂窩（內凹六邊形）材料的面內沖擊動力學性能。

2 結果討論與分析

2.1 具有負泊松比效應蜂窩材料的面內沖擊響應

圖7中給出了不同沖擊速度下內凹六邊形蜂窩在名義應變ε＝0.4時的面內沖擊變形模式。計算結果表明，由于胞元內凹，蜂窩材料的局部應力分布發生了改變。當胞元擴張角較小（如θ＝－5°）時，在低速沖擊（v＝7m／s）作用下，局部變形帶主要集中在沖擊端和固定端，變形帶內的胞元沿橫向（x方向）表現出局部剛化的特性。從試件的整體變形模態可知，靠近自由邊界的胞元處于受拉狀態，而處于縱向對稱軸附近中部的胞元處于受壓狀態。這也導致了試件的面內動力響應表現為某種軟芯材料（見圖7（a）中虛線）。隨著胞元擴張角的增加（θ＝－15°），由于塑性絞發生在各個結點處，更容易調動各個胞元發生整體變形，試件沖擊端和固定端局部變形帶消失，表現為整體均勻的變形模式。隨著胞元擴張角的進一步增加（θ＝－25°），試件的相對密度增大（見表1），固定端的胞元首先發生變形，當固定端胞元被壓潰之后，沖擊端胞元才開始變形。

隨著沖擊速度的增加（v＝20m／s），不同胞元擴張角蜂窩材料表現出各異的變形模態。當擴張角較小（θ＝－5°）時，變形主要集中在沖擊端，并且表現為V型剪切變形模式。隨著擴張角的增加，V型剪切變形帶逐漸減弱。當胞元擴張角更大（θ＝－25°）時，變形主要集中在沖擊端和固定端，且以沖擊端變形為主，與規則三角形蜂窩變形類似［11］。當沖擊速度接近或超過沖擊波速（v＝120m／s）時，慣性效應增強，變形帶主要集中在沖擊端，對應著從沖擊端到固定端I型逐層壓潰變形模式，這與其他微結構蜂窩材料基本類似［10－11］。可見，在沖擊荷載作用下，具有負泊松比效應蜂窩材料的面內沖擊響應主要依賴于胞元擴張角和沖擊速度。

圖7 具有負泊松比效應蜂窩材料在不同沖擊速度下的變形模式Fig.7 Deformation modes of honeycombs with negative Poisson’s ratio effects under different impact velocities

圖8中給出了具有負泊松比效應蜂窩材料沖擊端剛性板的面內沖擊響應曲線。計算結果表明，具有負泊松比效應蜂窩材料的動態響應規律與一般多胞材料相同，即開始階段，材料動態響應近似于線性；隨后進入穩定的平臺變形區，直至試件逐漸壓縮密實［1］。由于胞元擴張角的不同，蜂窩材料的動態響應各異。胞元擴張角的絕對值越大，試件的平臺應力越高，但由于相對密度的增加，鎖定應變卻相應減小，這種現象隨沖擊速度增加而更加明顯（見圖8）。圖9中給出了具有負泊松比效應蜂窩材料在固定端的動態響應曲線。在低速沖擊荷載（v＝7m／s）作用下，動態響應規律與沖擊端基本類似（見圖8（a）、圖9（a））。隨著沖擊速度的增加，胞元擴張角對固定端動態響應影響逐漸明顯，胞元擴張角的絕對值越小，固定端輸出應力越小。尤其在高速沖擊荷載作用下，這種現象尤為顯著（見圖9（c）、9（d））。

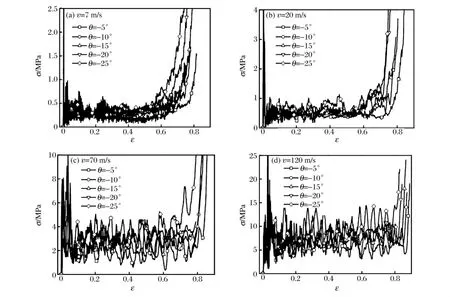
圖8 具有負泊松比效應蜂窩材料在沖擊端的名義應力應變曲線Fig.8 Nominal stress－strain curves for honeycombs with negative Poisson’s ratio effects at the impact end

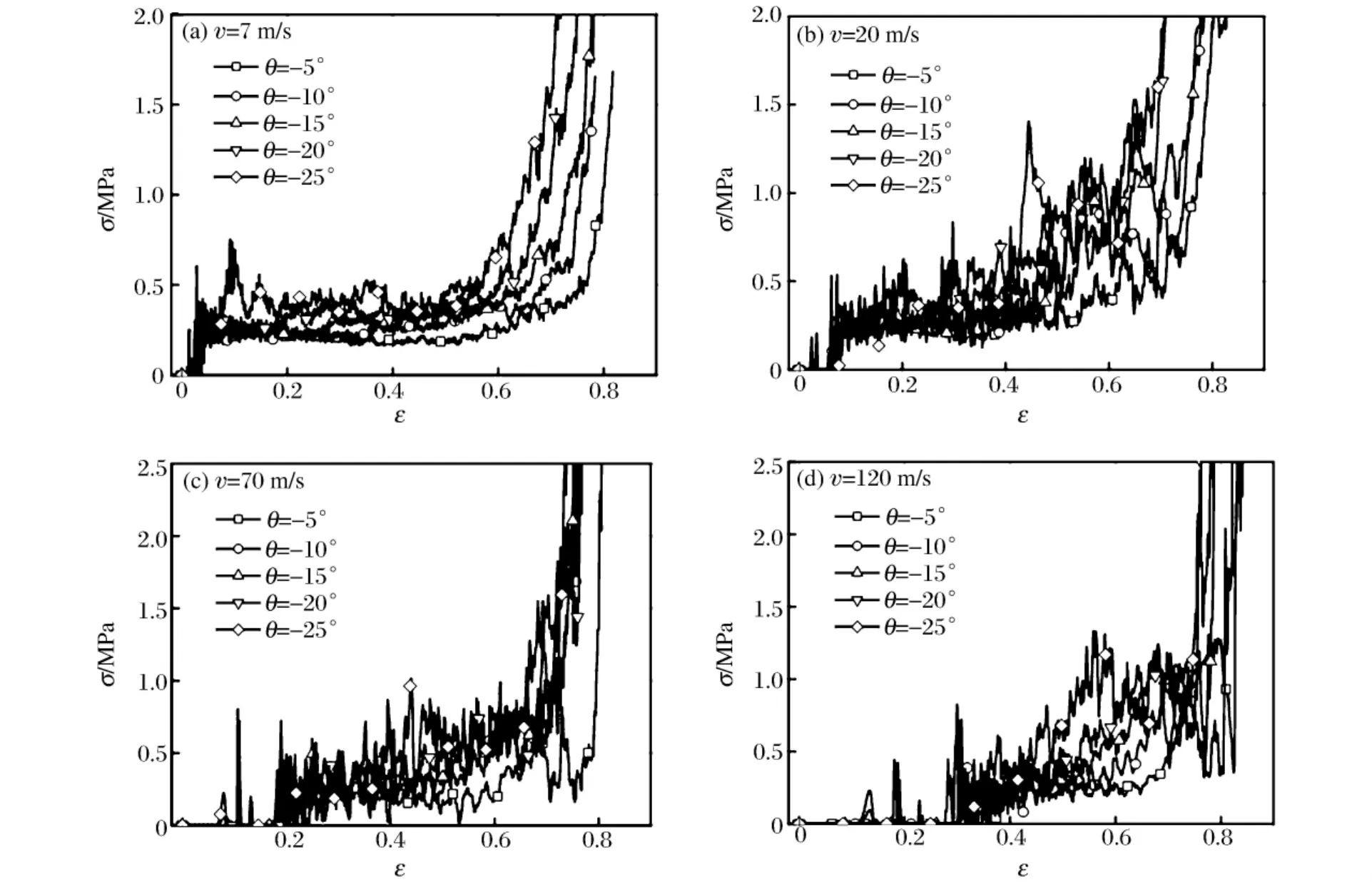
圖9 具有負泊松比效應蜂窩材料在固定端的名義應力應變曲線Fig.9 Nominal stress－strain curves for honeycombs with negative Poisson’s ratio effects at the supporting end

2.2 平臺應力與質量能量吸收

作為一種高效的阻尼材料，輕質多胞材料已被廣泛地應用于各種能量吸收結構中，從各種器件的包裝到航空航天飛機的能量吸收器。評估多胞材料與結構能量吸收能力大小的一個重要指標就是質量能量吸收率（即比能量）［12］

式中：εd為鎖定應變，可由名義應力再次達到初始應力峰值時所對應的應變確定；εcr為屈服應變，為名義壓縮應力達到第一個應力峰值時的名義應變，本文中取εcr＝0.02，以達到較高的計算精度；σ（ε）為隨名義應變而變化的名義應力。基于方程（3），圖10中給出了不同沖擊速度作用下具有負泊松比效應蜂窩材料在沖擊端和固定端的平臺應力。計算結果表明，沖擊端蜂窩材料的平臺應力都隨沖擊速度的增加而增大，與沖擊速度的平方幾乎成正比。對于相同的沖擊速度，蜂窩材料的平臺應力隨胞元擴張角絕對值的增加而增大（見圖10（a）、圖11），這也從另一方面反映了蜂窩材料應力分布的不均勻性。與蜂窩材料在沖擊端的平臺應力類似，固定端平臺應力也隨胞元擴張角的增加而增大，但隨沖擊速度的增加卻基本保持不變（見圖10（b））。

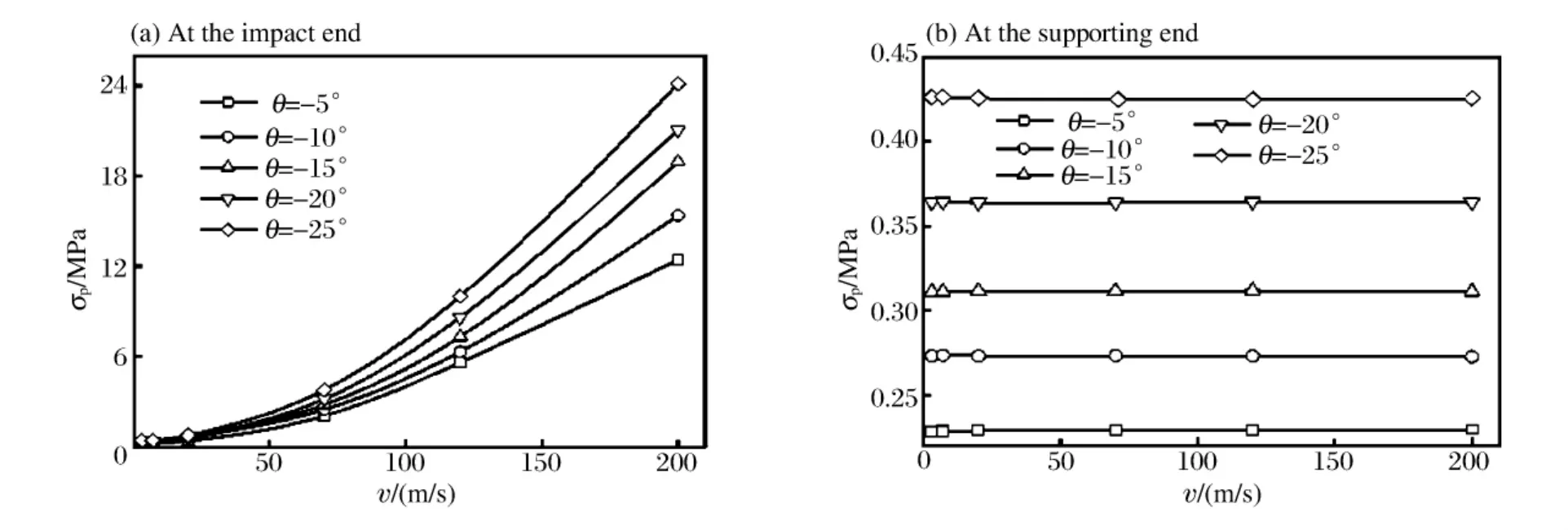
圖10 不同沖擊速度下具有負泊松比效應蜂窩材料的平臺應力Fig.10 Plateau stress for honeycombs with negative Poisson’s ratio effects under different impact velocities

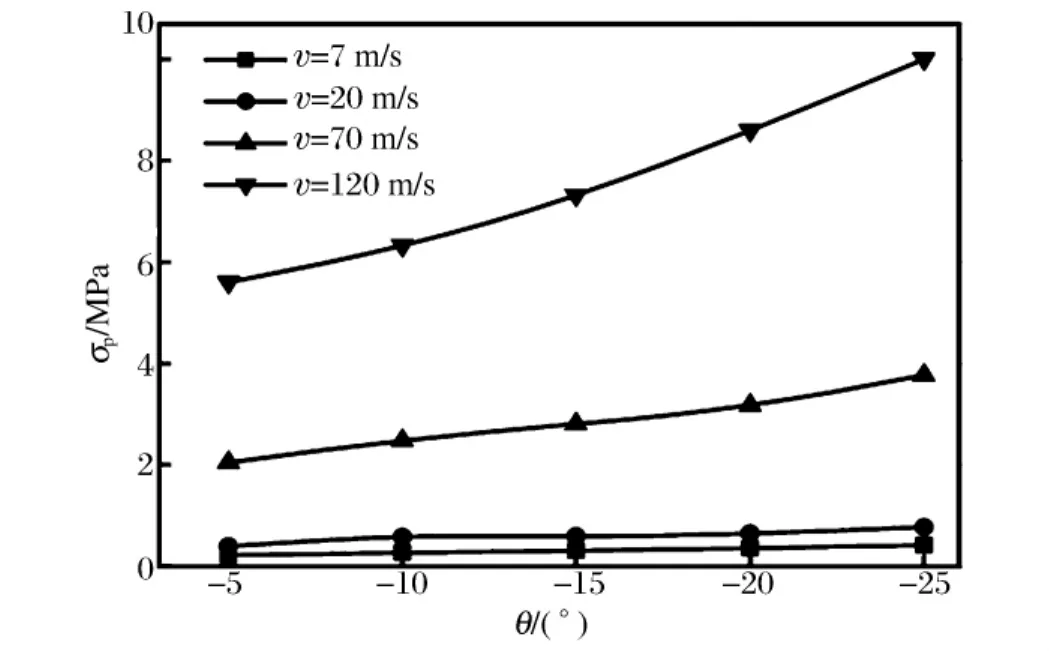
圖11 蜂窩材料沖擊端的平臺應力隨擴張角的變化Fig.11 Variation of plateau stress with respect to expanding angles for honeycombs at the impact end

基于方程（2），圖12中給出了具有負泊松比效應蜂窩材料質量能量吸收率與名義應變的關系。由圖12可見，在胞元幾何尺寸（壁長和壁厚）、材料的相對壓縮量和沖擊速度不變的前提下，胞元擴張角的絕對值越大，蜂窩材料的吸收質量能量越高。一方面，由于胞元擴張角的增加，相對密度相應增加；另一方面，胞元擴張角越大，試件面內變形更加困難。當胞元擴張角增加到一定值時，試件質量吸收能量變化很小。另外，由圖12也可見，隨著沖擊速度的增加，慣性效應增強，在名義應變一定的條件下，具有負泊松比效應蜂窩材料表現出更強的能量吸收能力。

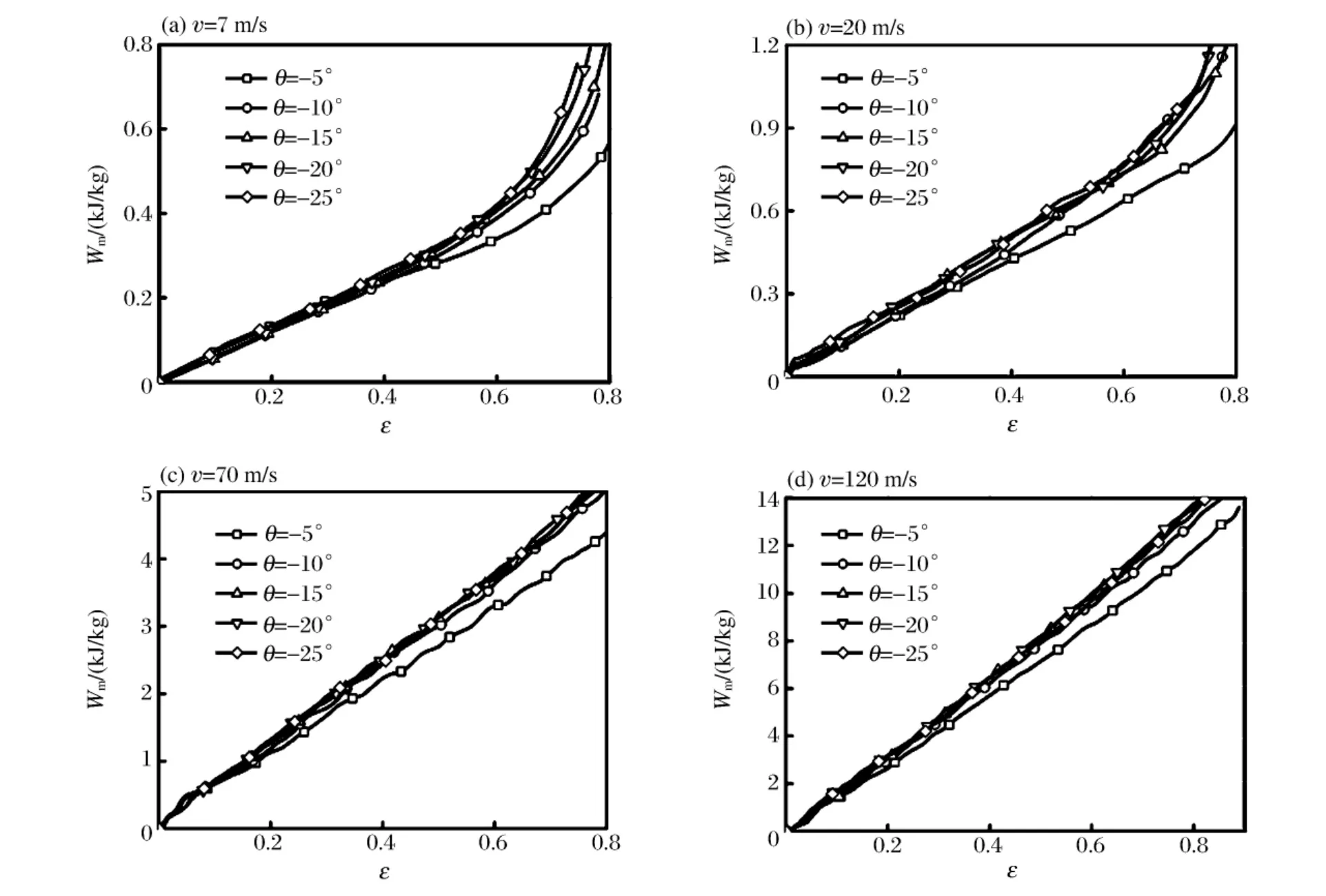
圖12 具有負泊松比效應蜂窩材料的能量吸收特性Fig.12 Energy absorption characteristics for honeycombs with negative Poisson’s ratio effects

3 結 論

針對具有相同幾何結構參數（胞元壁長和壁厚）、但不同胞元擴張角的內凹六邊形蜂窩，研究了不同沖擊荷載作用下蜂窩材料的面內動態沖擊特性。研究結果表明，具有負泊松比效應蜂窩材料的面內變形模式主要依賴于胞元擴張角和沖擊速度。胞元擴張角的不同改變了蜂窩材料中應力波的傳播特性，材料的局部變形模式發生了變化，進而影響了材料的宏觀動態響應。在中低速沖擊作用下，隨著胞元擴張角的增加，試件的動力學響應或者表現為某種軟芯材料（θ＝－5°），或者表現為整體變形模式（θ＝－15°），或者表現為局部剪切變形帶主要集中在沖擊端和固定端 （θ＝－25°）。在胞元壁長和壁厚、名義應變以及沖擊速度一定的前提下，胞元擴張角的絕對值越大，沖擊端蜂窩材料的平臺應力越高。與蜂窩材料在沖擊端的平臺應力類似，固定端的平臺應力也隨胞元擴張角的增加而增大，但平臺應力隨沖擊速度的增加卻基本保持不變。另外，隨著沖擊速度的提高，在名義應變一定的條件下，蜂窩材料表現出更強的能量吸收能力。

［1］Gibson L J，Ashby M F.Cellular solids：Structure and properties［M］.Cambridge：Cambridge University Press，1997.

［2］Lakes R S.Deformation mechanisms in negative Poisson’s ratio materials：Structural aspects［J］.Journal of Materials Science，1991，26（9）：2287－2292.

［3］盧子興，趙亞斌.一種有負泊松比效應的二維多胞材料力學模型［J］.北京航空航天大學學報，2006，32（5）：594－597.LU Zi－xing，ZHAO Ya－bin.Mechanical model of two－dimensional cellular materials with negative Poisson’s ratio［J］.Journal of Beijing University of Aeronautics and Astronautics，2006，32（5）：594－597.

［4］Choi J B，Lakes R S.Analysis of elastic modulus of conventional foams and of re－entrant foam materials with a negative Poisson’s ratio［J］.International Journal of Mechanical Sciences，1995，37（1）：51－59.

［5］Overaker D W，Cuitino A M，Langrana N A.Effects of morphology and orientation on the behavior of two－dimensional hexagonal foams and application in a re－entrant foam anchor model［J］.Mechanics of Materials，1998，29（1）：43－52.

［6］Wan H，Ohtaki H，Kotosaka S，et al.A study of negative Poisson’s ratios in auxetic honeycombs based on a large deflection model［J］.European Journal of Mechanics：A／Solids，2004，23（1）：95－106.

［7］Grima J N，Gatt R，Ravirala N，et al.Negative Poisson’s ratios in cellular foam materials［J］.Materials Science and Engineering：A，2006，423（1／2）：214－218.

［8］Horrigan E J，Smith C W，Scarpa F L，et al.Simulated optimisation of disordered structures with negative Poisson’s ratios［J］.Mechanics of Materials，2009，41（8）：919－927.

［9］Hallquist J O.LS－DYNA Theoretical manual［Z］.Livermore Software Technology Corporation，1998.

［10］Ruan D，Lu G，Wang B，et al.In－plane dynamic crushing of honeycombs：A finite element study［J］.International Journal of Impact Engineering，2003，28（2）：161－182.

［11］Liu Y，Zhang X C.The influence of cell micro－topology on the in－plane dynamic crushing of honeycombs［J］.International Journal of Impact Engineering，2009，36（1）：98－109.

［12］Kooistra G W，Deshpande V S，Wadley H N G.Compressive behavior of age hardenable tetrahedral lattice truss structures made from aluminum［J］.Acta Materialia，2004，52（14）：4229－4237.