有限域切比雪夫多項式算法性能測試與分析

劉亮

(中央電視臺新聞制作部，北京100859)

在L.Kocarev和Z.Tasev首次利用切比雪夫多項式的混沌特性構造了一種公鑰加密算法［1］后，很快 Pina Bergamo 等就對其進行了破解［2］。文獻［3］通過將切比雪夫多項式擴展到有限域上，使得文獻［2］的攻擊方式對其無效，并進一步提出了具體的公鑰算法。文獻［4］通過理論證明和實驗分析，解決了文獻［3］中忽略的切比雪夫多項式在有限域上仍然可能存在破解方法［5-6］，指出有限域切比雪夫多項式作為公鑰加密體系的基礎是可行的。

本文對文獻［3］所提出的密鑰協商、公鑰加密和數字簽名算法做了具體的編程實現，并對其計算性能進行了精確的測量。然后，結合有限域切比雪夫多項式的性質對實驗數據進行分析，并選擇一定的比較策略和相應的安全參數，將之與公鑰體系中常用的RSA、ELGAMAL和ECC算法性能進行比較。發現有限域切比雪夫多項式算法具有加密簡單，計算量小，處理速度快，存儲空間占用小和所需帶寬小的優勢，更加適合于帶寬有限的無線公鑰加密系統。

1 有限域切比雪夫多項式的矩陣迭代算法及其計算量

有限域切比雪夫多項式算法的迭代形式如下:

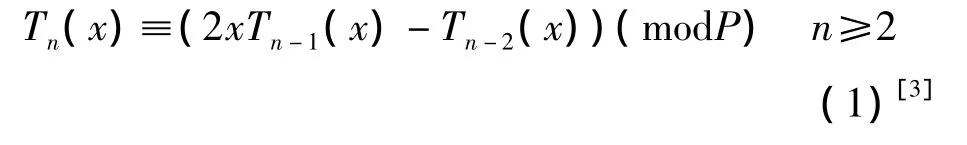
其中 n∈Z，變量 x∈ZP，多項式 Tn(x):ZP→ZP。

在編程實驗中，采用矩陣迭代方法，利用系數矩陣的累乘簡化了代數多項式的迭代計算的復雜性，關系式如下:

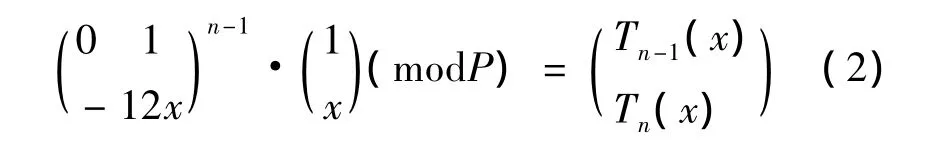
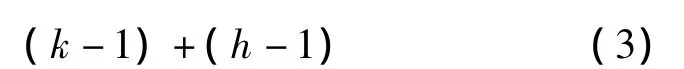
其中，k是n轉換成二進制表示時的總位數;h是n轉換成二進制表示時1的總個數，即漢明距。又因為0＜h＜k，所以有如下計算量關系:

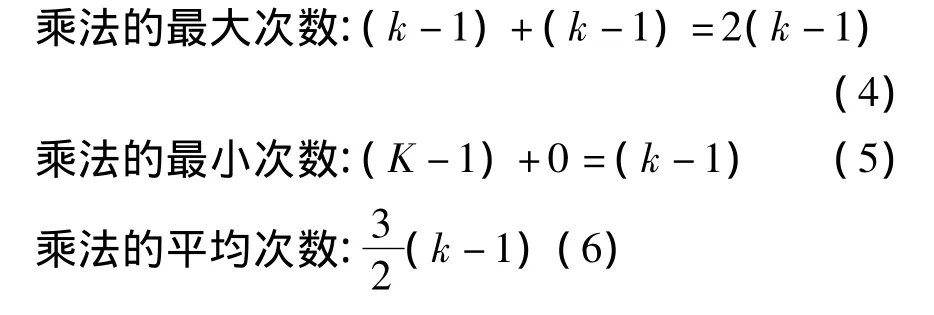
其中，式(3)是在已知比特位數n和漢明距h的情況下的精確的次數，而式(6)是在只知道比特位數n而不知道漢明距h的情況下的估算次數。

2 測試參數的選擇

2.1 安全參數的選擇

現有公鑰體系中常用的非對稱加密算法主要分為三類:

1)大整數分解難題(integer factorization problem，IFP):如 RSA;

2)離散對數難題(discrete logarithm problem，DLP):如 ElGamal，DSA;

3)橢圓曲線離散對數難題(elliptic curve discrete logarithm problem，ECDLP):如 EC ElGamal，ECDSA。

而一個系統的安全性主要取決于它自身算法的幾個安全參數，比如:RSA的安全參數是它的模N。DLP的安全參數有兩個，一個是它的群生成元p，一個是它的子群生成元q，它們都是素數;ECDLP的安全參數是它的橢圓曲線點所組成的加法群的生成元n。這些安全參數是相應算法的安全保障，同時它也是破解的主要對象。安全度相同時，三者的安全參數滿足關系如下:

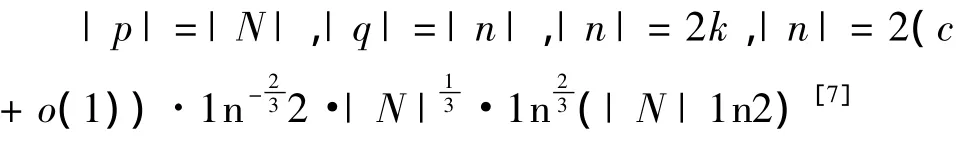
其中，|n|表示其中參數的比特長度，k是對稱加密算法的密鑰長度。表1給出了相同安全度下，這三種加密算法安全參數的比特長度。

表1 安全參數的比特長度

有限域切比雪夫多項式的安全度是由生成域Zp決定的。因此，素數P就是有限域切比雪夫多項式加密系統的安全參數，對應著RSA的N和Elgamal的p。又由于目前只有窮舉搜索可以有效地破解基于有限域切比雪夫多項式的加密體系，因此，它的安全度可以類比于對稱密鑰加密算法。于是，對應表1中安全參數的比特位數，選擇一系列測試域(P)進行實驗，如表2所示。

表2 測試域P的選取

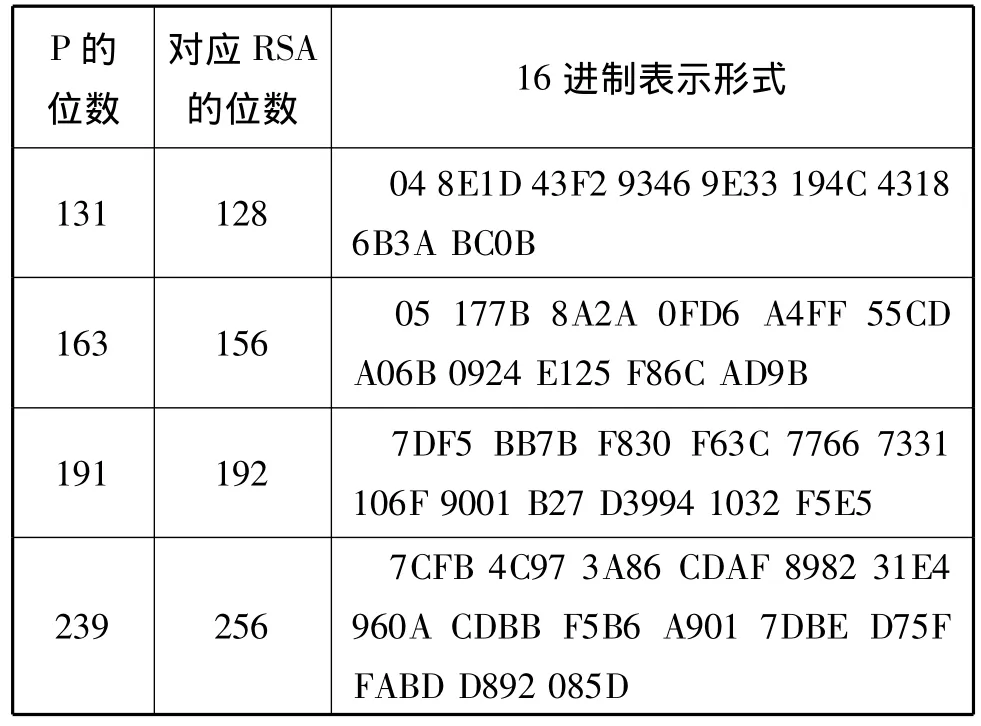
續表

2.2 公鑰x和私鑰n的選擇

由于性能測試主要針對有限域切比雪夫多項式常規算法的密鑰生成時間、加/解密時間、簽名和驗證簽名時間以及密鑰協商時間，因此，可以不考慮有限域切比雪夫多項式中易破解的特殊點［4］，而在域內隨機選擇x和n。

另外，由于x的值對計算時間影響很小，可以忽略不計，而n的取值卻對計算時間有較大影響。因此，在具體測試中，將根據實驗不同的側重點對n做一定的設置或限制。

3 測試方案及測試結果

3.1 單次矩陣乘法時間

實驗中，將不同域下一次系數矩陣乘法的時間作為標準單位，以獲得較精確的算法性能。具體測試時，首先選擇一個域(即P)，接著隨機生成一個x，然后選取一個n值。采用式(3)計算乘法次數。同時，設ni=1(i=0…k)，即n轉換為二進制后的各位全為1。這樣，乘法次數就達到最大，為2(k+1)，測試精度也就達到最高。需要注意的是，對不同的域，要選取不同的n，使得n較接近P，以達到較好的效果。

由于在具體的實驗中采用的是一般的PC機(奔騰 4代 CPU，主頻 2.5GHz，256M 內存)，WIN2000 SERVER的操作系統和VC6的編譯環境結合GNU大數運算庫，因此整個實驗環境的精度就不太高。所以，在每個域，對同一個n值測量10次，每次隨機生成x，以獲得現有條件基礎上較理想的測試結果。同時還對每一次乘法反復測量1000次，以減小系統時間的分辨率低，而每次計算的時間短對測試結果精度的影響。由此，便形成了兩個循環嵌套，將兩個循環的時間累加，然后在循環外做一次除法，便得到較高精度的某一域中一次矩陣乘法所用的時間。再對不同的域重復上述算法，得到不同域的單次矩陣乘法所用的時間。如表3所示，其中，P的取值同表2對應。

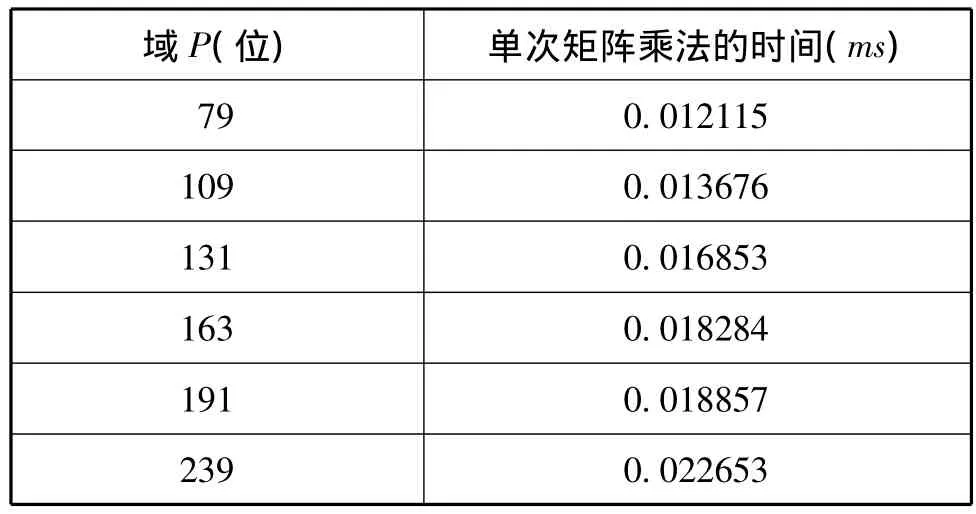
表3 不同域下單次矩陣乘法時間

3.2 密鑰生成和加、解密時間

這里，不需要準確的知道n轉換成二進制表示后的漢明距，而只需要知道n的位數，然后利用式(6)估算出平均矩陣乘法次數，再用測量到的時間除以平均矩陣乘法次數得到的時間與表3中不同域下單次矩陣乘法時間進行比較，便可以知道兩者是否在方法誤差范圍的許可內一致。從而進一步推出不同域下密鑰生成和加、解密的最大時間(n等于P-2)和最小時間(n等于1)，得知其計算時間的范圍和平均計算時間。

為了比較不同域下密鑰生成和加、解密的時間，我們把切比雪夫多項式計算中的n都設定為40位的隨機數，P和x的選取同3.1。仍舊采用3.1中的雙重循環嵌套的方法，進行多次測量再取平均值以獲得最佳測試結果。測試中，采用文獻［3］中的加、解密方案，設密鑰生成過程中的SK為40位，加密過程中的R也為40位，得到測試結果如表4所示。

3.3 簽名、驗證簽名及密鑰協商時間

由于數字簽名、驗證簽名以及密鑰協商也都是基于有限域切比雪夫多項式構造，因此測試方法同3.2中密鑰生成和加解密時間。

表4 不同域下密鑰生成和加、解密時間

測試簽名和驗證簽名時間時，采用文獻［3］中的簽名和驗證簽名的方案。P的取值同表3，簽名過程中簽名的私鑰SK為40位，簽名的消息M也為40位，得到測試結果如表5所示。

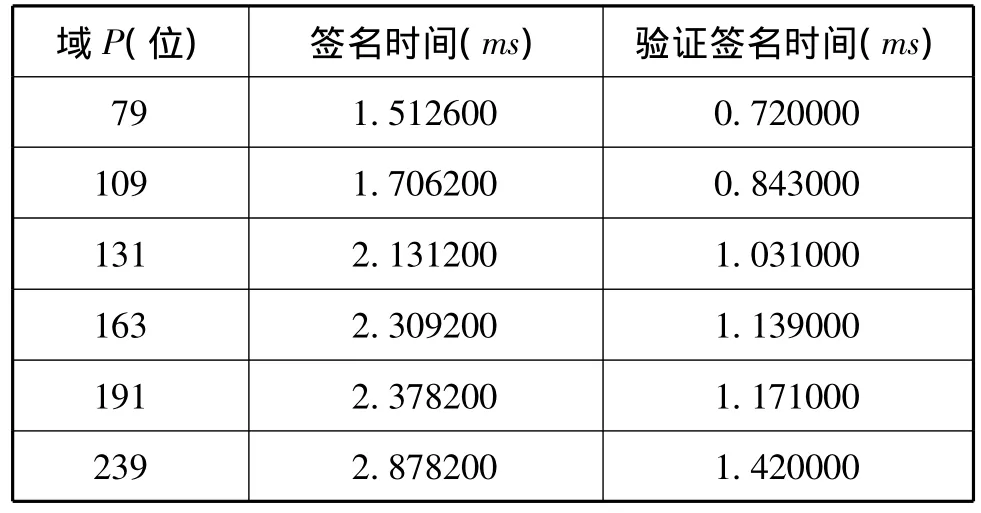
表5 不同域下簽名和驗證簽名時間

測試密鑰協商時，采用文獻［3］中的密鑰協商算法。P的取值同表3，Alice和Bob的協商密鑰KA和KB都為40位，得到測試結果如表6所示。

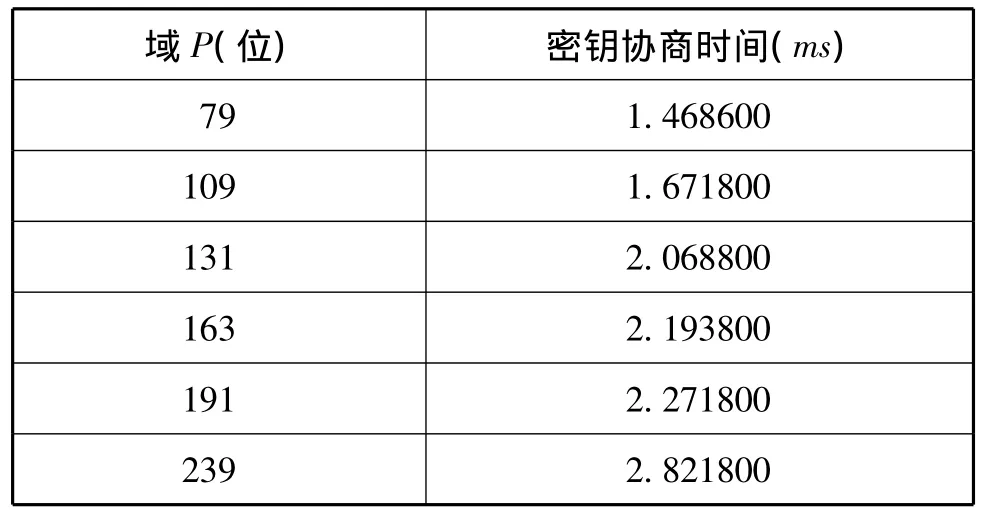
表6 密鑰協商時間

4 實驗數據分析

從表3-6可以看出，隨著P位數的增加，域越來越大，單次矩陣乘法時間、密鑰生成和加解密時間、簽名和驗證簽名時間以及密鑰協商時間都隨之增加。這是符合密碼學特性的，因為P是基于有限域切比雪夫多項式的公鑰體系的安全參數，而安全參數越大則計算量越大，計算時間越長［7］。此外，模運算更加復雜導致的計算量增大也是計算時間增加的原因。

還可以看到，隨著P位數的不斷增加，盡管計算時間變長，但是計算時間的增加幅度比P位數的增加幅度要小很多。這就使得在設計基于有限域切比雪夫多項式的公鑰體系時，可以通過不斷增大P的位數來獲得更高的安全性，而由于計算時間增加并不顯著，因此，整個公鑰體系的性能仍能保持較高，從而保證一定的效率。

由表4-6看到密鑰協商的時間同加密和簽名的時間大致相同，而約是密鑰生成、驗證簽名和解密時間的兩倍。這是因為，前者都進行兩次有限域切比雪夫多項式計算，而后者都只進行了一次有限域切比雪夫多項式計算，又由于它們在計算時選擇的n都是40位，所以得出的數據有以上規律。這說明，測得實驗數據同理論分析是相符的。

另外，可以利用表4-6中的測試數據估算出不同算法得單次矩陣乘法時間。結果，在相同域中，它們與表3中精確測量出來的單次的矩陣乘法時間極為接近。這就更加肯定了算法的正確性，為算法性能的評測提供依據。

5 有限域切比雪夫多項式算法在WPKI中的優勢

由上述測試數據可以看出有限域切比雪夫多項式作為公鑰算法相對于RSA和Elgamal算法具備如下優勢。

(1)安全性更高。由于它本身數學難題的復雜度高于RSA和Elgamal所基于的數學難題，因此，其抗攻擊性具有絕對的優勢。又由于目前針對它并沒有有效的破解方法，所以，它的安全性近似對稱密鑰加密系統。

(2)計算量小，處理速度快，存儲空間小，帶寬要求低。由于有限域切比雪夫多項式所需的安全參數位數低，密鑰尺寸小，因此它整個系統的計算速度就快，效率高，而所需的存儲空間相對就小，對帶寬要求也低。這對無線終端來說是非常重要的。

(3)密鑰的生成和選取更加靈活方便。RSA和Elgamal算法本身對密鑰的選擇就有很高要求，而有限域切比雪夫多項式算法對密鑰的選擇可以十分隨意［4］，因此，整個公鑰系統開銷也可以大大降低。

同ECC相比，有限域切比雪夫多項式算法優勢如下:

(1)數學原理通俗簡單，便于采用。ECC算法建立的數學模型相對來說比較復雜晦澀，給算法的具體實現和推廣帶來不少麻煩。而有限域切比雪夫多項式算法卻是在原來切比雪夫多項式算法基礎上的改進，原理淺顯易懂，計算較前者也更加簡單，效率更高。

(2)加密簡單。ECC在利用公鑰進行加密時需要計算點(x1，y1)=kP(k個P相⊕)，同時要防止點(x2，y2)=kQ 中的 x2=0，否則，就要重新選取［7］。而有限域切比雪夫多項式算法實現的條件寬松得多［4］。

由此可以看出，有限域切比雪夫多項式算法具備了RSA、Elgamal和ECC的優點，而鄙棄了它們的缺點。因此，可以將其很好的應用于WPKI體系的數字證書中。

6 結論

本文對采用有限域切比雪夫多項式的密鑰協商、公鑰加密和數字簽名算法做了具體的編程實現，并選擇一定的比較策略和相應的安全參數，對其計算性能進行了精確的測量。然后，結合有限域切比雪夫多項式的性質對實驗數據進行分析，并將之與公鑰體系中常用的RSA、Elgamal和ECC算法性能和應用進行比較。得知有限域切比雪夫多項式算法具有安全性高，加密簡單，計算量小，處理速度快，存儲空間占用小和所需帶寬小的優勢，更加適合于帶寬有限，計算能力受限的無線公鑰加密系統。

［1］Kocarev L，Tasev Z.Public-key encryption based on Chebyshev maps［J］.The 2003 IEEE International Symposium on Circuits and Systems Proceedings，2003，28-31.

［2］P Bergamo，P D Arco，A D Santis.Security of public key cryptosystems based on Chebyshev polynomials［OL］.http://citebase.eprints.org，2004.

［3］寧紅宙，劉云，何德全.基于有限域上 Chebyshev多項式的新公鑰加密系統［J］.

［4］劉亮，劉云，寧紅宙.公鑰體系中切比雪夫多項式的改進與特性研究［J］.北京交通大學學報，2005.

［5］G Maze.Algebraic Methods for Constructing oneway Trapdoor Functions［D］.Notre Dame:University of Notre Dame，2003

［6］Yoshimura T，Kohda T.Resonance properties of Chebyshev chaotic sequences［J］.Proceedings of the 2004 International Symposium on Circuits and Systems Volume 4 New York:IEEE，2004，23-26.

［7］L Fibìkov，J Vyskoc.Practical cryptography-the key size problem:PGP after year［J］.2001，11.