基于壓縮感知的核磁共振圖像重建的Bregman方法

楊曉蘭，朱永貴，叢佳，劉平

(中國傳媒大學理學院，北京 100024)

基于壓縮感知的核磁共振圖像重建的Bregman方法

楊曉蘭，朱永貴，叢佳，劉平

(中國傳媒大學理學院，北京 100024)

由于一些器官的邊界信息在大多數(shù)核磁共振圖像中都是稀疏的，所以利用壓縮感知從數(shù)量非常有限的觀測數(shù)據(jù)集合中重構同樣的核磁共振圖像并且大大減少核磁共振圖像的掃描磨損成為可能。然而，為了能夠做到這一點，我們必須要解決定義在大量數(shù)據(jù)集合上的非光滑函數(shù)的最小化這一困難問題。為了解決這一問題，我們給出了一個有效算法，它克服以往求解l1問題的計算復雜性，提出β范數(shù)近似逼近l1范數(shù)的思想，由于β范數(shù)具有光滑性，可采用Bregman迭代正則化方法進行求解。數(shù)值實驗證明，核磁共振圖像可以從全部數(shù)據(jù)的40%抽樣中幾乎精確重構。

壓縮感知；核磁共振成像；重構算法；Bregman方法

1 引言

對于壓縮感知成像，其目的是盡可能減少探測單元數(shù)量，更精確的重構出圖像。因此在感知信息獲取投影方面，該方面的研究需要沿著以下幾個方面進行：(a)投影方法的選擇，投影方法需要滿足以下三個條件：1)在信息采集方面，能夠使需要進行的測量盡量少；2)便于投影方法的硬件實現(xiàn)和優(yōu)化算法的迭代運算；3)能夠適用于大多數(shù)的稀疏情況。(b)尋找穩(wěn)定性更高，重建精度更好的重構算法，使得獲得的圖像的精度滿足實際應用需要。

如今，成像在醫(yī)療診斷方面起到了著非常重要的作用。事實表明減少掃描時間非常重要，即減少核磁共振成像所需要的時間，那就意味著在保證圖像質量的情況下，盡可能少地從頻域中收集觀測數(shù)據(jù)。然而，這看上去直接違背了長期以來建立的奈奎斯特標準：即所獲得的觀測數(shù)據(jù)的數(shù)量必須至少與恢復圖像所需要的信息數(shù)量相匹配。這就意味著完美的圖像重構將是不可能的，但壓縮感知允許我們在沒有相關噪聲的情況下重構圖像。

我們給出了一個有效算法，它克服以往求解l1問題的計算復雜性，提出β范數(shù)近似逼近范數(shù)的思想，由于β范數(shù)具有光滑性，可采用Bregman迭代正則化方法進行求解。數(shù)值實驗證明，核磁共振圖像可以從全部數(shù)據(jù)的40%抽樣中幾乎精確重構。

2 基于壓縮感知的核磁共振圖像重建的Bregman方法

通過壓縮感知我們得到b=Ru，其中傳感矩陣R是大小為m×n的矩陣。現(xiàn)在若想通過已經得到的b恢復出原信號u，則通過直接求解上述方程組是無法得到，因為上述方程組的未知數(shù)個數(shù)n大于方程個數(shù)m。如果一個方程組中未知數(shù)個數(shù)多于方程個數(shù)，則一般有無窮解，通常的求解方法為[1]：

(1)尋求更多的方程；

(2)選自由變量，給一組線性無關的值后，進行求解。

如果未知u的其它信息，則上述逆問題很難求得唯一解。但若信號u是k-稀疏的，設m≥k·log(n)，則上述方程組可以求解，因為此時未知數(shù)個數(shù)事實上只有k個。盡管如此，由于我們并不知道u中哪些分量為零，所以不能直接求解，而是通過下式求最稀疏的向量，從而獲得u：

(2.1)

其中‖·‖0表示u中非零元素的個數(shù)。然而，盡管從理論上來講，這種方法可以實現(xiàn)，但是在實際中不可行，因為這是一個組合問題(NP難問題)，計算量非常大。因此我們需要尋求合適的范數(shù)來近似求解上述問題。采用l1范數(shù)最小化求得的解，為稀疏向量，非常接近最小化l0范數(shù)所得的真實解。因此，我們可以選擇l1范數(shù)最小化來近似求解上述優(yōu)化問題，即

(2.2)

剛才討論的信號u本身是稀疏的，接下來討論信號u本身并不稀疏，但是可以壓縮的情況。我們需要將信號變換到變換域考慮。設Ф是壓縮基(如小波基)或緊框架，滿足規(guī)范正交，即Ф*Ф=I，作變換Фu=x，顯然x是稀疏的。于是在這種情況下的求解方法為：

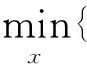
(2.3)

其中A=RФ-1，并且要求m≥μ2(R，Ф-1)·k·logn。

以上考慮的都是等式約束，然而實際中，測量過程可能會引入噪聲，這時約束條件式中的Ax=b必須被放松，從而引出問題

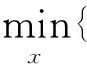
(2.4)

或者問題

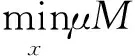
(2.5)

其中σ與μ是參數(shù)。從最優(yōu)化理論上來說，問題(2.4)和(2.5)在某種意義上是等價的，解決了其中一個問題就能決定另一個問題的參數(shù)，使得它倆能夠給出相同的解[2]。

我們將提出β范數(shù)近似逼近l1范數(shù)的思想，他克服了以往求解l1問題的計算復雜性的問題，由于β范數(shù)具有光滑性，使得模型可采用Bregman迭代正則化方法進行求解。

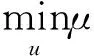
(2.6)

令J(u)=μ|u|β，基于凸函數(shù)J(u)的u，v之間的Bregman距離定義為：

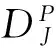
p∈?J(v)是J在v點的次微分中的某一個次梯度。

可通過求解：

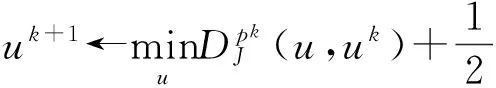
(2.8)

k=0，1，2，3…

u0=0，p0=0(k=0為原始問題(2.6))來替代對(2.6)問題的求解，其證明參見文獻[3]。

因為J(u)不是處處可微，故J(u)的次微分可能包含不止一個元素，從(2.8)中uk+1的最優(yōu)性，對(2.8)關于u求偏導再以uk+1替換可以得到：

0∈?J(uk+1)-pk+A*(Auk+1-b)

因此令：

pk+1=pk+A*b-A*Auk+1。

(2.8)與(2.6)的區(qū)別在于正則化的應用，(2.6)通過直接最小化u的β-范數(shù)將其正則化，而(2.8)是通過最小化u的基于β-范數(shù)的Bregman距離將其正則化。

文獻[3]中的數(shù)值結果表明，當u足夠大，這一簡單迭代過程明顯改進了原始模型(2.6)的去噪能力。

除了對于迭代過程k=0，對于所有的k，(2.8)可以演繹為問題(2.6)只要滿足：

bk+1：=b+(bk-Auk)
b0=u0=0

其初始條件為：b0=u0=0，因此迭代過程(2.8)可以等價于

(2.9)

(2.9)可以通過任意一種已存在的求解(2.6)的方法求解。

方法一：

u0←0，p0←0

(2.81)

Fork=0，1，…do

(2.82)

pk+1←pk-A*(Auk+1-b)

(2.83)

方法二：

b0←0，u0←0

(2.91)

Fork=0，1，…，N，do

bk+1=b+(bk-Auk)

(2.92)

(2.93)

在方法一中，給出uk，pk，uk+1滿足一階最優(yōu)條件：

0∈?J(uk+1)-pk+▽H(uk+1)
=?J(uk+1)-pk+A*(Auk+1-b)

因此：

pk+1=pk-A*(Auk+1-b)∈?J(uk+1)

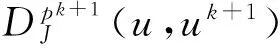
定理二表示Bregman迭代過程的方法一(2.81)-(2.83)，方法二(2.91)-(2.93)在(2.82)及(2.93)有相同的目標函數(shù)(達到同一個常量)的情況下是等價的。

由(2.91)可以得出：b1=b因此當k=0時，(2.82)(2.93)求解相同的最優(yōu)化問題：

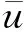
A*(b-Au)
=wF*P*(b-PFw-1u)

故：

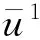
根據(jù)(2.83)p0=0，b=b1可以得到：

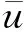
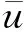
試證明：

(i) (2.82)(2.93)最優(yōu)化問題的第k次迭代是等價的

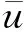
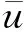
關于(i)的證明：由假設可知：

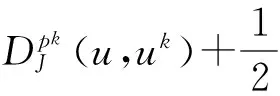
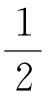
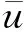
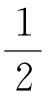
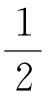
其中C1，C2，C3為常數(shù)，因此(2.82)(2.93)有相同的目標函數(shù)；

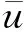
由(i)及[4]的結論可以得到；

關于(iii)的證明：根據(jù)假設以及(2.83)(2.92)，及(ii)可以得到：

pk+1=pk-A*(Auk+1-b)

=pk-wF*P*(PFw-1uk+1-b)

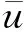
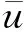
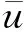
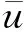
注：如果J不是嚴格凸函數(shù)，方法一、二也許會求的不止一個解，上面的證明過程告訴我們，即使方法一及方法二的某一步迭代產生了不同的中間值，他們之后還是會產生相同的結果。

(2.93)的每次迭代都是(2.6)的一個實例，都可以通過FPC(Fixed-point continuation Methed)[5]來求解，盡管對任何嚴格正的μ都能得到收斂的結果，我們還是要選取能使得(2.6)可以用FPC有效求解的μ，并且使得Bregman迭代的總時間是最優(yōu)的。

下面我們將求解模型：

(2.9)

bk+1=b+(bk-Auk)

此時u是近似稀疏信號，且A=PF指的是部分傅利葉變換，如果令x代表原始信號，w代表小波變換，那么可以得到u=wx，同樣的x=w-1u，因為在實際計算時，能直接得到并且可以做初值的是原始信號，所以需要對模型中的u做一個替換，用wx替換u，那么我們可以得到：

由于A=PF而w代表小波變換，對原始圖進行完小波變換后，不能直接對稀疏信號進行福利葉變換，故要對稀疏信號再進行一次逆小波變換再進行傅利葉變換，此時為使模型簡單，繼續(xù)用u=wx替換wx但同時要加入逆小波變換那么得到：

但是此時使A=PFw-1，下面我們就對上述模型進行計算推導。

令

令導數(shù)為0，那么式子變?yōu)椋?/p>

需要求解上式中的u，我們使用逐步遞歸的方法，用u(k+1)代替u得到：

在分母部分用u(k)代替u(k+1)，并且去分母，得到：

利用

b(k+1)←b+(b(k)-Au(k))

得到：

μu(k+1)+A*(Au(k+1)-b-(b(k)-Au(k)))

合并同類項得到：

由

A=PFw-1

A*A=(PFw-1)*(PFw-1)=wF*P*PFw-1

A*Au(k)=wF*P*PFw-1u(k)

A*=wF*P*

A*b=wF*P*b

那么就得到：

對兩邊同時進行逆小波變換、傅里葉變換。得到：

具體算法如下：

b0←0，u0←0
For：k=0，1，…，N，do
bk+1=b+(bk-Auk)

(3.0)

bk=bk+1
kk=uk+1

3 數(shù)值實驗

在壓縮的核磁共振成像中，采樣矩陣A是由A=RФ-1給出的，其中Ф是一個小波變換，R是一個部分二維離散傅里葉變換。假設一個核磁共振圖像有n個像素。在我們的算法中，R是從相應于一個完整的二維離散傅里葉變換的n×n階矩陣中隨機抽取m行組成的，即R=PF，其中P是從n×n階單位矩陣中隨機抽取m行組成的矩陣，F(xiàn)是二維離散傅里葉變換矩陣，m?n。所選的m行指出所選擇的頻率，在這些頻率中，b中的觀測數(shù)據(jù)被收集。m值越小，通過一個核磁共振掃描器來獲取b所需要的時間就越少。在核磁共振成像中，我們有一定的自由來選擇行(然而，實際的限制可能會影響我們的選擇，但是這已經超出了這篇論文的討論范圍)。在我們的實驗中，由R估量得出的傅里葉系數(shù)并不是在隨機的頻率中選取的。我們是通過以下方式來選擇的：在k-space中，我們分別采取了兩種不同采樣方法進行試驗：一種采樣是沿著一定數(shù)量的從中心散開的呈輻射狀的直線來選取，即半徑抽樣。例如圖4.1顯示了在一個k-space中的22*5條輻射狀直線，即這是22*5 views抽樣頻域圖；另一種則是矩形采樣，例如圖4.2顯示了在一個中采樣的區(qū)域(白色部分為采樣區(qū)域)。我們發(fā)現(xiàn)這種選擇允許我們從數(shù)量較少的采樣數(shù)據(jù)中，而不是整體隨機采樣選擇來恢復方形的核磁共振圖像。實際上，在一個核磁共振成像掃描中，頻率的集合以及采樣的速度都是受物理和心理極限限制的，所以我們的采樣方法是理想化的。

白色顯示的是采樣位置，這時的采樣率是圖1：42.38%，圖2：42.95%。

圖1 圖2

(3.1)

我們在256×256的心臟原始圖像核磁共振圖像上檢測我們的編碼。在所有的檢測問題中，采用的噪聲是均值為0方差為0.01的高斯白噪聲。對256×256的心臟原始圖像進行110 views、66views、22 views頻域抽樣，重構的圖像如圖3每組圖中圖(a)為原始圖像圖(b)、(c)、(d)為恢復后圖像。然后，我們再對256×256的心臟原始圖像進行矩形區(qū)域抽樣，重構的圖像如圖4示，每組圖中圖(a)為原始圖像，圖(b)、(c)、(d)為恢復后圖像。

在數(shù)值試驗中，相對誤差(Relative Error)和信噪比(Signal to Noise Rations，簡稱SNR)用來評估重構圖像的質量。相對誤差和信噪比的定義如下：

(3.2)

(3.3)

(a) (b)

(c) (d)

圖3(a)是原始心臟圖像；(b)、(c)和(d)分別是恢復后的圖像，它們的采樣率分別是42.18%、26.85%和9.36%。

(a) (b)

(c) (d)

圖4 (a)是原始心臟動脈圖像；(b)、(c)和(d)是恢復后的圖像，它們的采樣率分別是42.95%、24.29%和14.44%．

圖5 半徑采樣下相對誤差、信噪比CPU時間與采樣率之間的關系

圖6 矩形采樣下相對誤差、信噪比、CPU時間與采樣率之間的關系

表1半徑采樣下核磁共振圖像重建實驗結果：

表1

表2矩形采樣下核磁共振圖像重建實驗結果

表2

4 結論

在這篇論文中，基于壓縮感知理論，我們通過較少數(shù)量的觀測數(shù)據(jù)來恢復核磁共振圖像，對此，我們研發(fā)了一個有效算法，它克服以往求解問題的計算復雜性，提出β范數(shù)近似逼近l1范數(shù)的思想，由于β范數(shù)具有光滑性，可采用Bregman迭代正則化方法進行求解，這在l1問題的求解方面是一種新穎的方法。在真實的核磁共振圖像上進行的數(shù)值實驗表明，這種算法可以在采樣率相對較小的情況下，使用不到一分鐘的時間來恢復忠實于原圖的正方形圖像。通過對相對誤差、信噪比和CPU時間的對比，我們知道通過使用最優(yōu)化技巧，例如光滑以及更有效的線性搜索等，我們的算法速度仍然可以加快。然而，本論文未能就Bregman法的收斂速度進行系統(tǒng)分析，對這種方法的理論分析也缺乏詳細的研究，這些問題要留待以后再解決。另外，我們認為，這篇論文中所闡述的壓縮感知的算法可以被延拓到其他相關的圖像以及可視化的應用中。

[1]Osher S，Burger M，Goldfarb D，Xu J，Yin W.An iterated regularization method for total variation-based image restoration，Multiscale Model.Simul[J].2005，4：460-489.

[2]趙瑞珍.壓縮傳感與稀疏重構的理論及應用[EB/OL].中國科技論文在線http：//www.paper.edu.cn

[3]Nocedal J，Wright S.Numerical Optimization.Springer[M].New York，2nd edition，2006.

[4]Rudin L I ，Stanley Osher.Total Variation Based Image Reatoration with free local constratints[C]. Image Processing，ICIP-94，1994，1：31-35.

[5]Gilbert A C，Muthukrishnan S，Strauss M J. Improved time bounds for nearoptimal sparse Fourier representation [ A] .Proceedings of SPIE，Wavelets XI [ C] .Bellingham WA：International Society for Optical Engineering，2005，5914：1215.

(責任編輯：王 謙)

TheBregmanMethedResearchonImageReconstructionBasedonCompressiveSensing

YANG Xiao-lan，ZHU Yong-gui，CONG Jia，LIU Ping

(School of Sciences，Communication University of China，Beijing 100024，China)

Because information such as boundaries of organs is very sparse in most MR images，compressed sensing makes it possible to reconstruct the same MR images from a very limited set of measurements significantly reducing the MRI scan duration.In order to do that，however，one has to solve the difficult problem of minimizing nonsmooth functions on large data sets.To handle this，we propose an efficient algorithm that It has overcome the computational complexity of solving thel1problem，this paper puts forwardβnorm approximationl1norm thought，becauseβnorm with slickness，one can use Bregman iterative regularization method to solve this problem.The numerical experiments demonstrate that original MR images can be reconstructed exactly from the mere 40 percent of the complete set of measurements by our approach.

compressed sensing；magnetic resonance imaging；reconstruction algorithm；The Bregman methed

2012-06-06

中國傳媒大學理科規(guī)劃項目(XNL1105)

楊曉蘭(1985-)，女(滿族)，新疆昌吉人，中國傳媒大學理學院碩士研究生.E-mail：yxlan_2010@163.com

TP391

A

1673-4793(2012)04-0018-09