船用堆堆芯控制棒分布對圍板/反射層不連續因子的影響分析
滕辰 蔡琦 陳玉清
(海軍工程大學船舶與動力學院,武漢 430033)
0 引言
船用堆存在非均勻性,引入等效均勻化理論[1]計算包含不連續因子在內的組件均勻化參數后,反應堆靜態物理特性的模擬精度得到顯著提高。但是船用反應堆控制棒大距離移動積分價值的計算上仍存在明顯的誤差,堆芯外圍的四組、五組控制棒問題尤為突出。通過分析,發現僅僅利用一維模型對船用堆圍板/反射層節塊進行均勻化處理過于簡單。雖然可以滿足船用堆靜態物理特性的仿真精度,但無法反映堆芯控制棒棒態發生變化時引發的不對稱性對圍板/反射層均勻化參數尤其是不連續因子的影響。參考文獻[2]中的二維圍板/反射層計算方法,結合 TPFAP中的穿透概率模塊編寫了圍板/反射層等效均勻化參數計算模塊TPBWRHP并通過了ZION算例的驗證。利用該模塊對不同棒態下圍板/反射層節塊進行了計算分析,并結合非線性迭代半解析節塊方法[4]程序對全堆進行擴散計算。計算結果表明,考慮堆內控制棒狀分布態變化對圍板/反射層節塊的影響,能夠有效跟蹤控制棒價值隨棒位的變化特性。
1 等效均勻化理論介紹
傳統均勻化方法假定組件的界面凈中子流為零并把注意力集中到單個節塊的反應率守恒上,忽略了均勻化區域凈中子流的守恒。這一假定對于大型電站堆芯的組件計算來說能較好的吻合,但對于小型船用壓水堆來說,由于它存在較大的非均勻性,會給組件計算帶來較大的誤差。
等效均勻化方法則首先是保證區域交界面上的中子流守恒。但是,這也導致了區域交界面上均勻化后的中子通量不連續,因此需要引入不連續因子來保證區域交界面上的非均勻中子通量連續。非均勻中子通量連續關系可用下式表示:
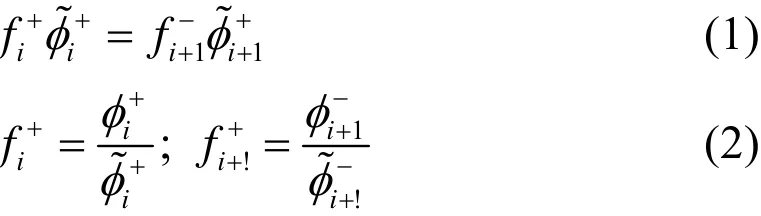
2 圍板/反射層等效均勻化參數的計算
通過修改TPFAP中的穿透概率模塊使之能對組件進行非對稱計算,并利用它對全堆芯進行輸運計算,求出圍板/反射層節塊的非均勻中子通量分布以及面中子通量和凈中子流分布,然后利用邊界凈中子流為零的條件求解圍板/反射層節塊的二維擴散方程獲取節塊面通量的均勻解,最后利用式(2)計算不連續因子。
對每個均勻化圍板/反射層節塊,考慮均勻化區域[5],{(x,y):-h1/2≤x≤h1/2; -h2/2≤y≤h2/2},h1為節塊的寬度,h2為節塊的長度,如圖1所示。建立無源節塊兩群擴散方程為[6]:

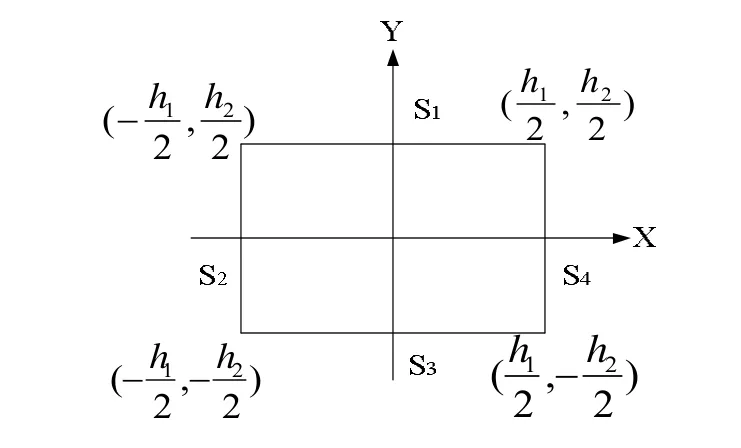
圖1 節塊坐標示意圖
經過兩維非均勻輸運計算,可以得到圍板/反射層區域內中子通量及面平均中子通量和面平均中子流的非均勻輸運解的具體分布。因此,可以用非均勻中子流作為節塊的邊界條件,具體分布可參見圖2。文獻[5]求解系數過程中的方程組達到八階,太過復雜。可以將方程化為四個二階方程進行解析求解,更有利于程序編寫。

觀察上述方程可以發現,系數a1,b1所在的等式與a2,b2所在等式是不相關的。因此可以對兩個二階方程進行求解。又因sinh(x)為奇函數, cosh(x)為偶函數的特點可將上述方程進一步簡化:

所以容易求得系數:
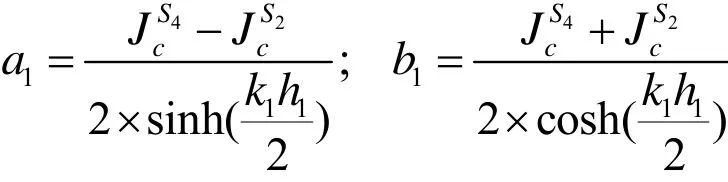
求出方程系數后,求取節塊均勻化后表面的平均中子通量。沿節塊的每個表面對中子通量做積分[5]:
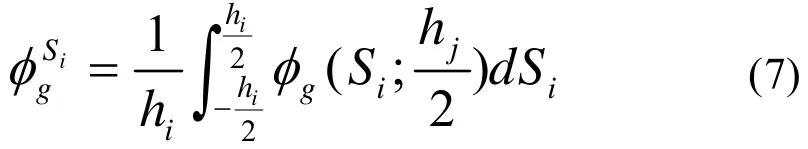
其中,si為積分面;hi為該面的長度;hi/2為該面的不變坐標值;g=1,2。由不連續因子的定義,可以得到每個節塊每個面上的不連續因子是:

其中,‘het’和‘hom’分別表示非均勻化的結果和均勻化的結果。
3 船用堆芯外層組件與反射層的非均勻性分析
3.1 堆芯外層組件非均勻性分析
船用反應堆組件橫截面呈方形,由圓柱形燃料柵元緊密排列而成,內部對稱布置有多個孔道,其中可以是水洞、可燃毒物棒、控制棒等。水洞對中子的慢化效果十分明顯,可燃毒物棒和控制棒均具有大的吸收截面,控制棒的棒位變化在組件中形成了強吸收區域和水洞區域等都是造成反應堆非均勻性的主要原因。船用反應堆體積小,中子通量難以展平也是造成反應堆非均勻的另一個重要原因。圖3、4分別為利用TPFAP計算的含有多束控制棒的組件 M 和多個水洞的組件 N的熱中子歸一化通量分布趨勢圖。從圖中也可以發現中子在組件內分布與邊通量分布存在較大的梯度。根據TPFAP的計算得出組件M的熱群和快群不連續因子分別為1.333、1.085,組件N的熱群和快群不連續因子為:0.868、1.008。由此進一步說明了船用反應堆存在顯著的非均勻性。
3.2 圍板/反射層組件等效均勻化參數計算
船用壓水堆堆芯周圍設置有一定厚度的不銹鋼圍板,由于不銹鋼具有大的吸收截面,因而圍板對堆芯的功率分布有很大影響,尤其是對靠近它的組件影響更為突出。先進均勻化理論通過引入超組件計算[2]可以計算獲得圍板/反射層的中子泄漏譜,并利用入射中子流為零或邊界中子通量為零的邊界條件求出不連續因子。根據船用堆堆芯布置,我們將圍板/反射層與相鄰組件組成的超組件分為:①同時為水洞柵元,②同時為控制棒柵元,③時含有水洞和控制棒柵元三種情況進行計算。圖2為其中超組件③計算的簡化布置圖。計算結果見表1。
4 計算結果與分析
驗算一、冷態臨界下,計算四組棒和五組棒從歸一化棒位入落入堆芯時產生的總的積分價值;驗算二、熱態不同臨界棒位下,計算四組棒的積分價值。計算結果見表1、表2,從結果看考慮控制棒在堆芯的分布狀態對圍板/反射層的影響后可以將積分價值的計算誤差控制在 2% 以內,尤其對大距離移動的控制棒組的積分價值計算有明顯改進。
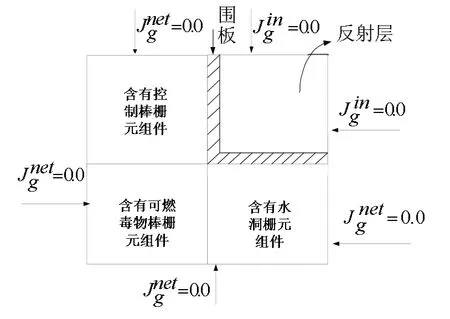
圖2 超組件示意圖
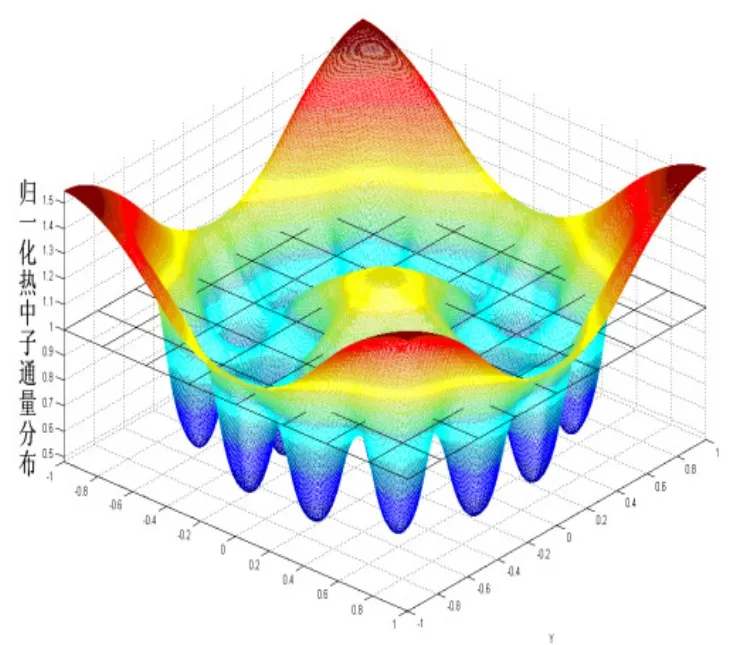
圖3 組件M熱中子歸一化分布圖
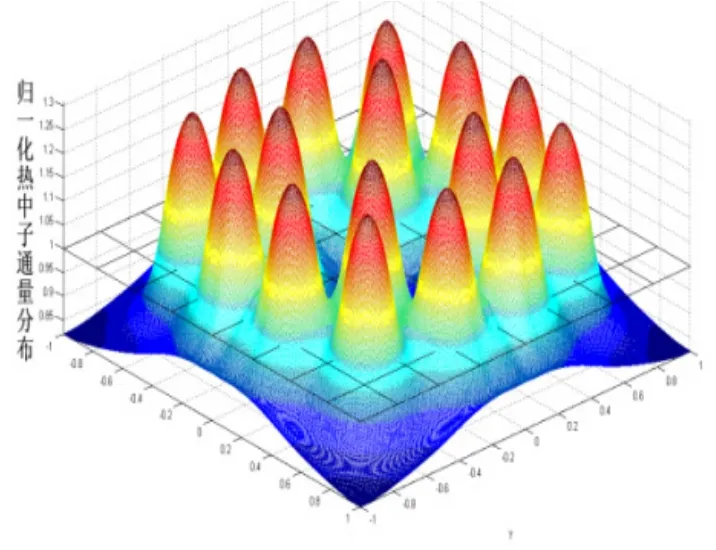
圖4 組件N熱中子歸一化分布圖
總的來說,不連續因子的計算和控制棒積分價值驗算結果進一步說明了船用壓水堆具有顯著的非均勻性。船用壓水堆的非均勻性主要由反應堆本身的堆結構所決定,同時控制棒在堆芯的分布也會對反應堆的非均勻性產生一定的影響。船用壓水堆堆芯最外層組件均是由含有多束控制棒的組件組成(分為四組和五組),組件本身含有強吸截面材料使組件產生了較大的非均勻性。同時四組和五組控制棒作為功率調節棒組,它們的棒位變化使堆芯中某一區域由含多束控制棒的組件變為含多個水洞的組件,影響了堆芯外層組件的快中子譜和熱中子譜以及堆芯外層泄漏中子譜的分布,也是反應堆存在顯著非均勻性的原因。充分考慮控制棒分布對圍板/反射層等效均勻化參數的影響是必要的。
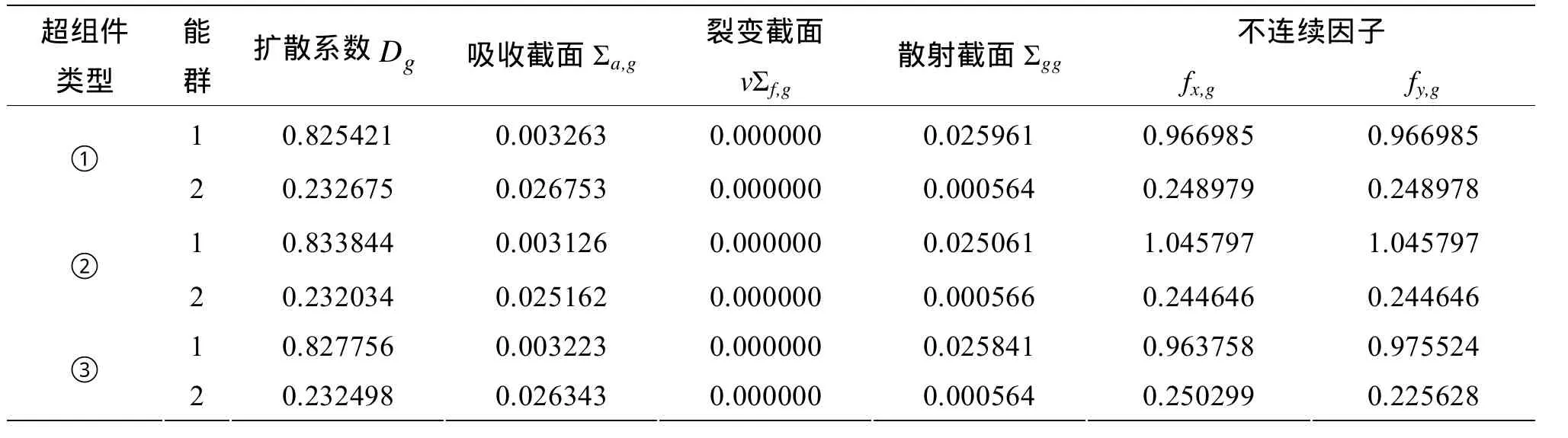
表1 冷態圍板/反射層等效均勻化參數

表2 冷態臨界下的積分價值計算結果
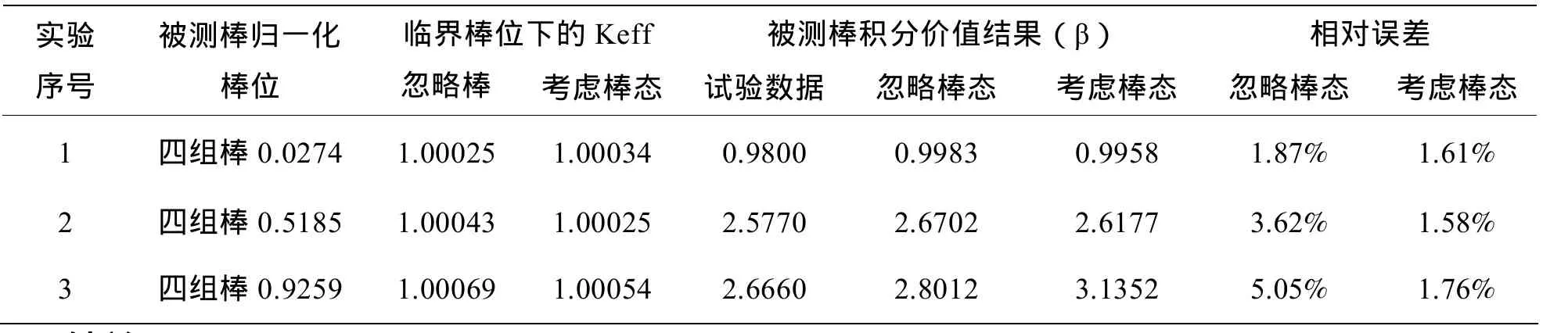
表3 熱態臨界下的積分價值計算結果
5 結論
1) 利用 TPFAP程序并通過添加的函數模塊成功地計算出了燃料組件以及圍板/反射層的不連續因子。
2) 經計算可知船用堆存在顯著的非均勻性,引入不連續因子理論能有效改善控制棒的計算精度。
3) 船用壓水堆的不均勻性除了與反應堆結構緊密相關外,還受到堆內控制棒分布變化的影響。
4) 通過計算結果與試驗的比對,文章進一步驗算了 NLSANM程序對船用堆的適用性和正確性。
[1]K.S. Smith. Assembly homogenization techniques for light water reactor analysis. Progress in Nuclear Energy, 17(13): 303-305, 1986.
[2]謝仲生. 壓水堆核電廠堆芯燃料管理計算及優化[M]. 原子能出版社, 2001.
[3]周旭華. 高溫氣冷堆控制棒區不連續因子的計算與應用[J]. 核動力工程, 2008, 29(6): 1-5.
[4]廖承奎. 求解穩態中子擴散方程的非線性迭代半解析節塊程序NLSANM程序手冊. 西安: 西安交通大學, 2002.
[5]王紅霞, 鐵水反射層參數均勻化計算[D]. 西安: 西安交通大學, 2002.
[6]謝仲生等, 核反應堆物理分析[M]. 北京: 原子能出版社, 1994.

