弓網系統動力學分析

宋 偉

0 引言

隨著國內鐵路技術的發展，列車運行速度的提高，其動態環境急劇惡化，空氣動力作用和輪軌間動力作用加劇，高速弓網受流問題復雜化，對受電弓-接觸網的動態特性提出越來越高的要求。因此，在鐵路高速化進程中，除了要研制高速機車車輛和線路結構外，還必須研究解決受電弓在接觸網下的高速受流問題，研究弓網動力學特性和受電弓的氣力學特性，只有這樣才能使電力機車從接觸網上可靠地獲取電力能源。

本文就針對該問題，對受電弓的線性化模型的運動微分方程進行推導，與接觸網的有限元模型一起建立受電弓-接觸網系統垂向動力學模型，并利用中心差分法編寫了數值仿真程序；研究了列車運行速度、接觸網和受電弓參數對弓網系統動態接觸壓力的影響。

1 受電弓網模型及運動微分方程

1.1 受電弓模型及運動微分方程

國內電力機車上使用的受電弓多為單臂受電弓，在建立接觸懸掛的振動模型時，大都考慮了受電弓的作用及其影響，在進行計算機仿真時，通常都要對受電弓的單元歸算質量，因此目前研究受電弓的模型常采用歸算質量模型，歸算質量模型是利用動能等效原理將原結構簡化成幾個具有集總質量的模型。圖1列出一些比較常用的受電弓模型。

圖1 受電弓模型示意圖

對于受電弓線性化模型的建立，主要是對框架結構的線性化處理。假定受電弓的基座固定不動（即不考慮機車的振動），把受電弓底座的轉動換算到框架頂部的垂向運動。所以本文采用二元弓模型，如圖1 b所示。

根據牛頓定律得到受電弓運動微分方程組表達式為[1，2]

式中，M1、C1、K1、M2、C2、K2分別為受電弓模型中弓頭和框架的質量、阻尼、剛度；y1、y2分別為受電弓弓頭和框架的位移；y(x,t)為接觸線t時刻的位移；F0為靜態抬升力。

1.2 接觸網模型及振動微分方程

接觸網是架設在鐵路線上空，向電力機車供電的輸電線路，通過它與電力機車的受電弓直接滑行接觸，將電能傳遞給電力機車。接觸懸掛是由接觸線、承力索、吊弦及其相應的附屬裝置組成的連續空間機械系統。接觸懸掛若從整體講，是柔性狀態；若就局部而言，線索自身都具有一定剛度。為研究的方便[1]，任取接觸網一個微分段dx，其動態受力示意圖如圖2所示。

圖2 具有一定剛度的一個懸掛微分段受力分析圖

當受電弓以速度V勻速通過接觸網時，根據參考文獻[1]，得到具有一定剛度的接觸懸掛的振動微分方程

式中，EJ，T，ρ，KS，C，δ分別為接觸懸掛抗彎強度，接觸網張力，接觸網線密度，接觸剛度，阻尼系數，Dirac函數；Vt為t時刻受電弓的橫坐標，y(x,t)為接觸線t時刻的位移。

對于等截面簡支梁[3]

式中，qi(t)為廣義振型坐標，是時間t的函數；φn(x)為主振型函數。將式（3）代入式（2）中，將每一項乘以第n個振型函數φn(x)，沿梁的全長L積分，并考慮振型的正交性，第n階振型的廣義坐標運動方程為

對于等截面的簡支梁，振型函數可以假定為三角函數，這時

將上式代入式（4）中，并注意到

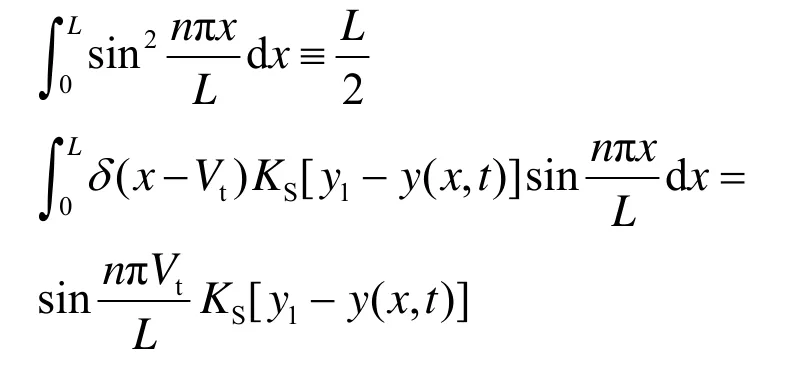
積分后得到

1.3 弓網系統耦合模型及動力學微分方程

為了模擬弓網之間的動態接觸行為，將接觸網模型和受電弓模型進行組合，整個弓網模型如圖2所示。聯立受電弓、接觸網的動力學平衡方程（1）和（7），就得到了不考慮機車振動時，受電弓-接觸網的動力學平衡方程組：

式（8）是一個無窮多自由度的聯立方程組。對接觸網來說，如果位移級數取N項，則整個接觸網的廣義自由度將為N個，加上受電弓的歸算質量M1，M2的自由度y1，y2。整個系統運動方程的N＋1階矩陣表達式

式中，Y、F、M、C、K分別為廣義位移矩陣、廣義力矩陣、廣義質量矩陣、阻尼矩陣和廣義剛度矩陣。

圖2 基于二元弓的弓-網耦合系統模型示意圖

2 仿真算法選擇

由于弓網系統數學模型的復雜性，進行弓網耦合振動分析，已遠遠超出了理論解析的范疇，必須要借助計算機進行數值仿真分析。目前工程中廣泛采用的數值分析方法有2種：隱式法和顯示法。隱式法目前常用的有 Newmark法、Houbolt法、Wilson-θ法、Hilber-Huhges法和Park方法等，其數值穩定性較好。顯示法有四階Runge-Kutta法和中心差分法，經典的線性多步法中不存在無條件穩定的顯示法。

在分析復雜的有限元系統時，要求逐步積分法是無條件穩定的，否則在積分過程中，結構高頻分量的反應會無限制地增長，而使整個積分失去意義。因此，本文仿真算法采用中心差分法[4]。

3 弓網系統動力學仿真

根據前面構建的受電弓-接觸網系統模型，得到弓網系統耦合運動微分方程組，利用中心差分法對弓網系統進行數值模擬，得到動態下的弓網接觸壓力變化曲線，其仿真流程圖如圖3所示。

圖3 弓網系統耦合動力學計算流程圖

利用中心差分法編寫弓網耦合仿真程序，并對不同車速下的弓網動態接觸壓力進行模擬仿真計算。接觸網采用簡單鏈形懸掛，受電弓和接觸網基本參數根據參考文獻[1，5]。圖4、圖5、圖6分別為列車運行速度80，120和160 km/h時弓網動態接觸壓力隨受電弓運動位置的變化曲線。

通過對弓網接觸壓力的仿真可以看出，在正常情況下弓網接觸壓力是沿跨距（65 m）呈周期性變化，在每一跨中的動態接觸壓力變化情況基本一致，即當受電弓通過支柱時，出現接觸壓力的峰值。這是因為接觸網支柱處不僅有集中質量，而且在支柱處接觸網彈性剛度較大，從而導致接觸壓力在受電弓通過此處時出現極值。同時由圖4—圖6可以看出，當列車在較低速運行時（80 km/h），接觸壓力變化較小，弓網保持良好接觸，受流情況良好。但隨著列車速度的不斷提高，弓網接觸壓力變化逐漸增大，對弓網受流產生較大影響。當運行速度提高到160 km/h時，接觸壓力變化劇烈，弓網受流質量變差。

圖4 速度為80 km/h時接觸壓力變化曲線圖

圖5 速度為120 km/h時接觸壓力變化曲線圖

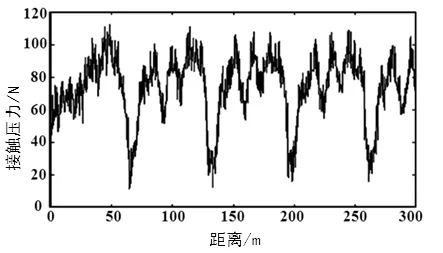
圖6 速度為160 km/h時接觸壓力變化曲線圖

4 結論

本文通過歐拉-拉格朗日方程推導出弓網系統振動微分方程組；利用中心差分法推出弓網數值仿真程序，并對不同工況下的弓網接觸壓力進行仿真及對比分析，得出結論如下：

（1）在低速行車條件下（80 km/h），弓網動態接觸壓力受車軌耦合振動影響較弱，可以忽略。

（2）隨著列車運行速度的提高（≥120 km/h），機車與軌道耦合振動增強，對弓網動態接觸壓力的影響也迅速加大。

由此可見，建立受電弓模型考慮弓網間相互作用高頻區段的影響，既可進一步完善弓網系統相關的數值分析技術，還可為新型高速受電弓的設計和弓網系統動力學特性的認知提供技術支撐。

[1]于萬聚.高速電氣化鐵路接觸網[M].成都：西南交通大學出版社，2003.

[2]于萬聚.接觸網設計及檢測原理[M].北京：中國鐵道出版社，1993.

[3]雷曉燕.軌道力學與工程新方法[M].北京：中國鐵道出版社，2002.

[4]蔡成標，翟婉明.高速鐵路受電弓-接觸網系統動態性能仿真研究[J].鐵道學報，1997，19（5）：38-43.

[5]Poetsch G, et.al.Pantograph/catenary dynamics and control.Vehicle System Dynamics, 1997, 30: 59-195.