一種改進的數字圖像置亂算法

黃 婕

(長沙航空職業技術學院，湖南 長沙 410014)

伴隨著人們對信息安全和保密意識的日益加強，數字圖像的置亂已成為一個重要的研究課題。目前，在信息隱藏技術方面確實取得了可喜的成績，［1］但與此同時信息攻擊者所采用的攻擊手段也在不斷進步，能否很好地保證信息的安全，是一個亟待解決的問題。而圖像置亂方法作為數字水印的一項基礎性工作，采用一定置亂方法的圖像能夠使水印圖像消除像素空間的相關性，從而失去水印信息原有的面貌，然后再將水印信息隱藏到載體里面。這樣，盡管攻擊者能將數字圖像從載體中提取出來，也無法分辨出經過置亂后圖像的信息。所以，對水印信息進行旋轉、置亂運算是很有必要的。

1 數字水印的旋轉算法

為了增強水印信號的保密性與安全性，消除像素空間的相關性，使攻擊者難以還原出水印圖像，先將二值水印轉化為實值圖像，然后進行旋轉、置亂處理，這樣，經過預處理后的水印圖像安全性有了進一步的提高。

文中使用的是二值水印圖像，其中二值水印的矩陣為:

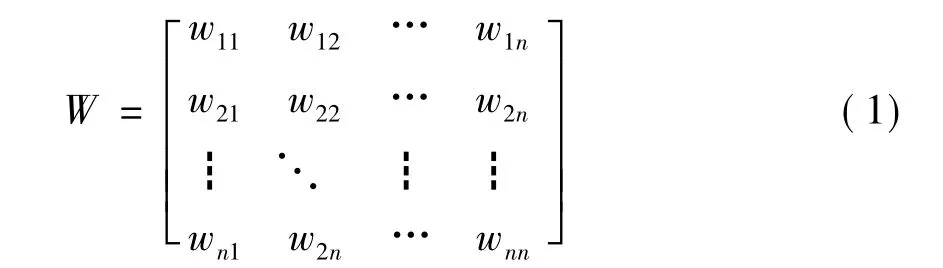
對矩陣W的對應元素進行行掃描，然后轉換為n2×1的向量，即:

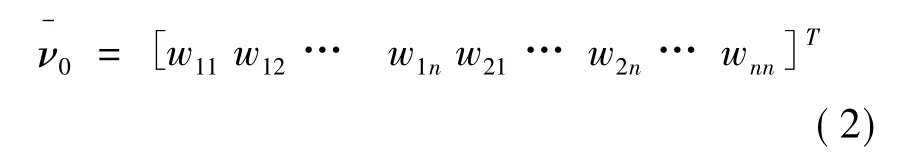
然后計算:

其中:

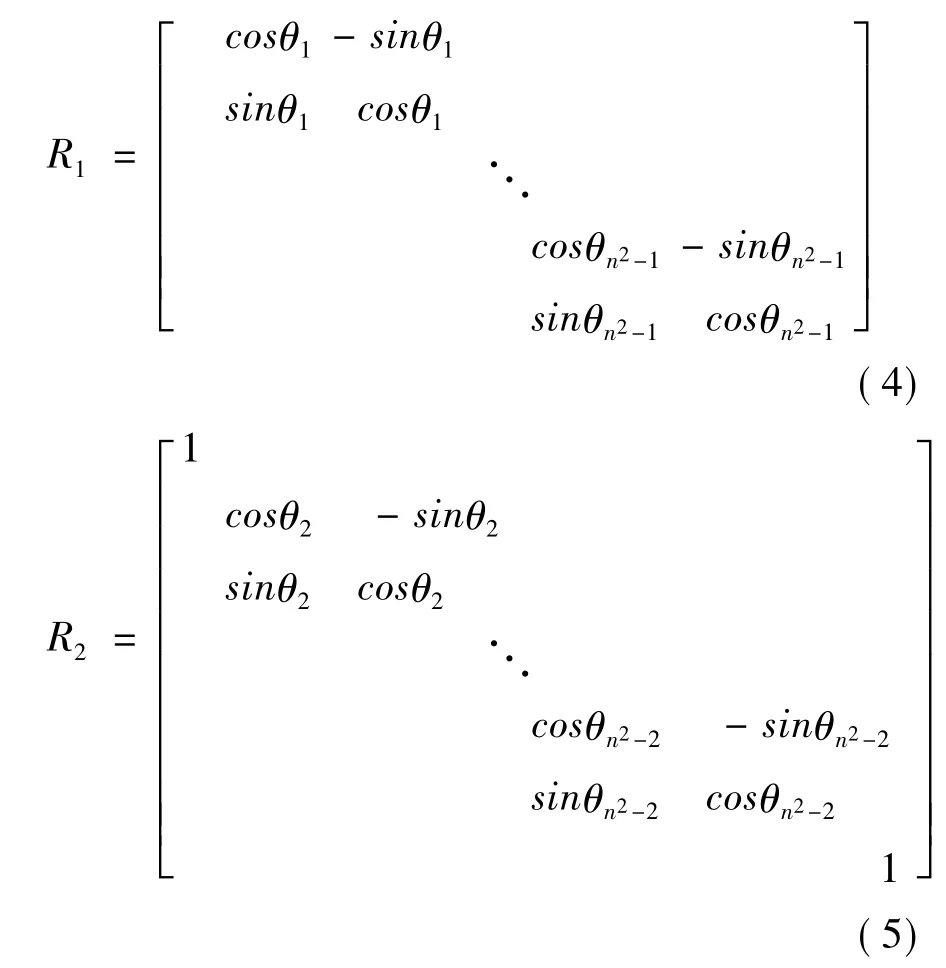
其中R1、R2是旋轉因子，作用是使旋轉后的圖像和原水印圖像的能量相等。所以，僅改變矩陣元素的位置，而不改變圖像的能量。

最后，再將n2×1的向量轉換為矩陣 Wt，Wt即為旋轉后的水印圖像對應的數據矩陣，其形式應為:

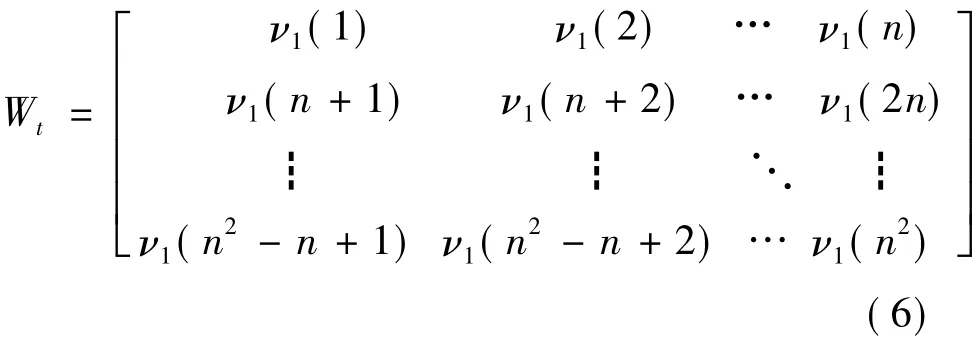
文中采用的水印信息為“HUST”二值水印圖像，旋轉算法在MATLAB語言中程序運行結果如下圖1，其中(a)為水印“HUST”的原始圖像，(b)為旋轉后的圖像:

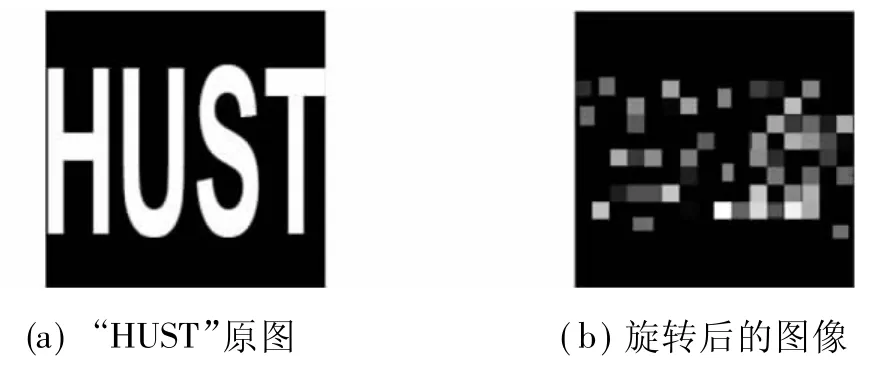
圖1 數字水印旋轉后的實驗結果

2 幾種常見的置亂方法

常見的置亂方法有幻方變換、Arnold變換、Hilbert變換等，各種變換均有差別，下面以兩種方法為例來介紹一些常用的置亂方法。

2.1 幻方變換

幻方是非常古老的數學問題。目前，幻方已經逐漸開發了它的應用。實際上，幻方與群論、組合分析等其他的分支有關聯。因此，幻方的價值有待人們進一步去探索，并發現其他廣泛的應用。［2－3］

n階矩陣:

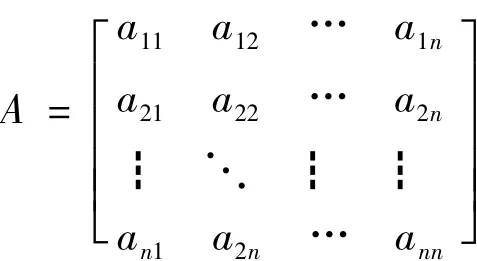
若元素符合以下性質:

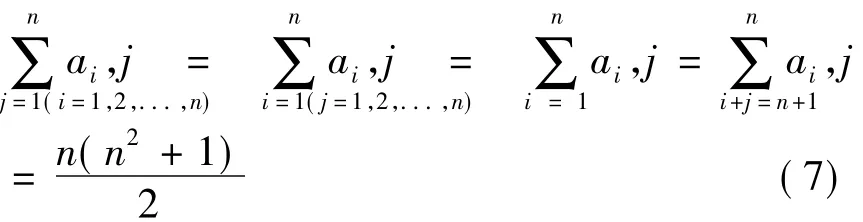
則稱矩陣A為幻方矩陣。

幻方變換就是根據幻方矩陣中的自然數序號元素來對圖像塊位置進行相應移動的位置變換，變換過程可寫為:

(1)使得A中自然數B＇=(A×B)modN序號元素一一對應于B中的像索點。

(2)使得A中的序號為m的元素后移一個單元，即 m+1 位置其中 m∈{1，2，...，n2－1}。使得A中位置為n2的元素移動到1的位置。

(3)B中元素隨著A中元素做相應變換。

于是，矩陣A變換成A1，矩陣B也變換B1，若A1=EA，那么B1=EB，E表示以上的操作。如圖2所示，圖中n=4，為一次幻方變換過程。不過一般情況下 A1，A2，...，An2－1不是標準幻方矩陣。當變換 n2次時，A=An2，B=Bn2，即幻方變換的變換周期為n2。幻方變換是具有一個周期性的過程的。

圖2 幻方變換過程

圖3為64*64*8的PANDA圖像經過變換后的效果。圖3(a)為原是圖像，圖3(b)、3(c)及圖3(d)分別為原始圖像經過16次、32次、4096次置亂的效果圖。

圖3 基于幻方變換的圖像置亂

2.2 Hilbert變換

Hilbert變換來源于，德國數學家 Hilbert在1891年，他利用一種不自交的曲線去遍歷正方形平面中所有點的方法，并且，有且僅有遍歷一次所有結點。因此，這種曲線取名為Hilbert曲線。按照Hilbert曲線的走向遍歷圖像中的所有點，可以不重復地訪問每一個節點，類似于幻方變換，得到變換圖像為Hilbert變換圖像。

若有一幅圖像，以Hilbert方法遍歷為例，其圖像對應矩陣的大小為4×4，假設入口點為矩陣左下角的結點，那么具體的做法如圖4所示。即矩陣A變換成A1，B變換成B1。

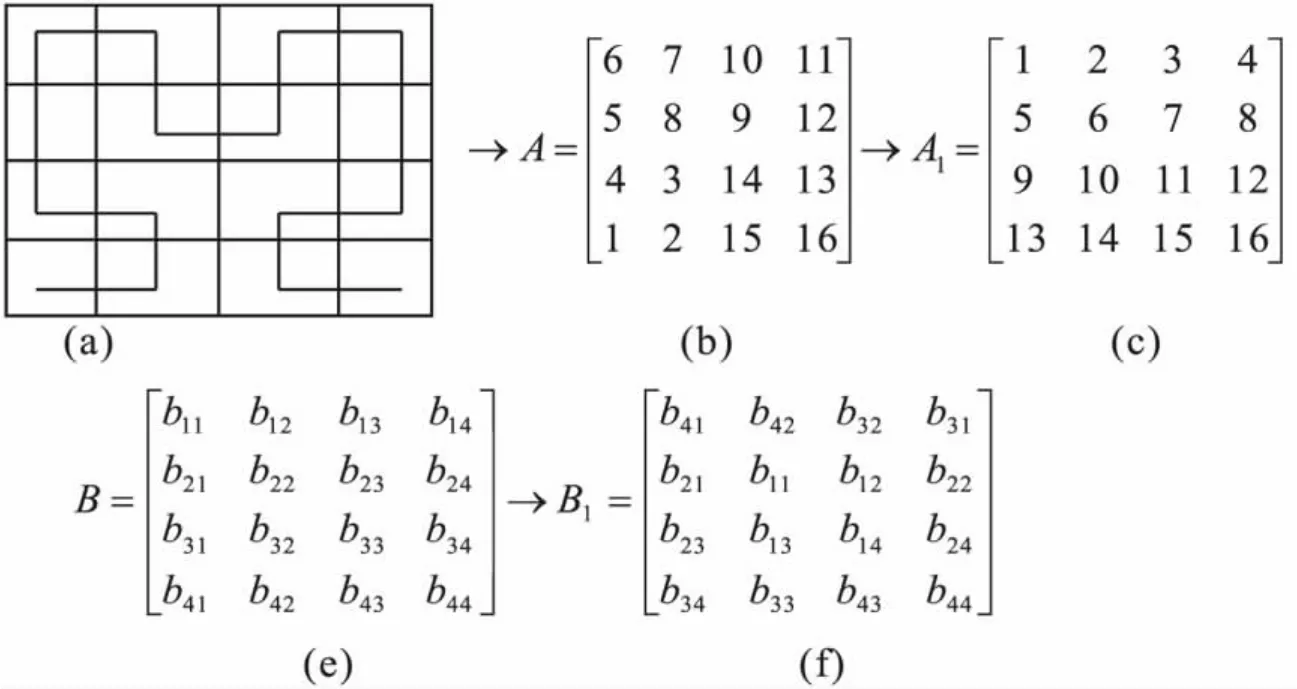
圖4 Hilbert變換示意

Hilbert曲線應用較廣泛，采用Hilbert置亂方法一方面可以對一維的水印信號置亂，同時也能將二維的水印信號置亂。文獻［4］［5］就采用了Hilbert置換技術進行數據的預處理工作。

3 GEMMER數字水印置亂算法

在我們分析了幾種常見的置亂方法的特點之后，給出了一種改進的的置亂算法—具有周期性的GEMMER置亂算法。

其基本步驟實現如下:

1)若對原始圖像進行L層的小波分解，即可產生一個任意長度的元素為非負整數的2L+2的向量;

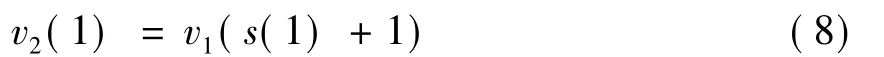
然后，將結果作為ν→2的第2個元素，即:

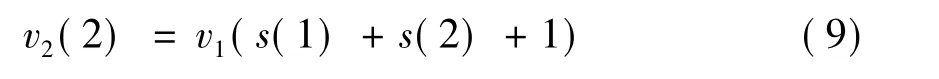
重復以上兩個過程，在n2步后，將得到向量。

3)將n2×1的向量ν→2轉換為矩陣Ws，Ws即為旋轉置亂后的水印圖像對應的數據矩陣，其形式應為:

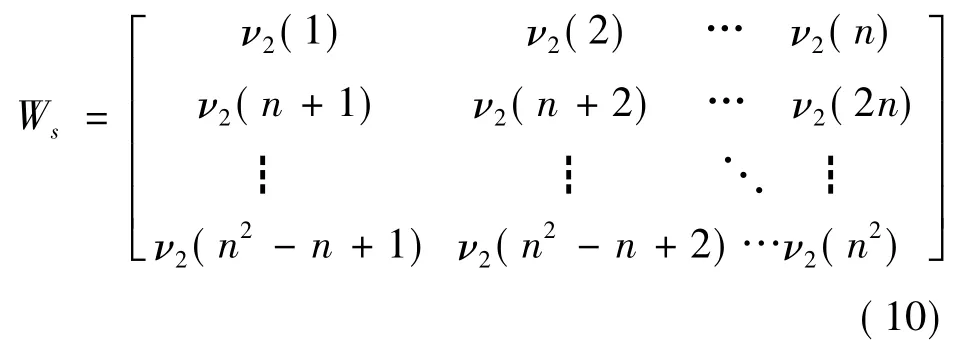
因此，該過程是一種可逆的過程。即原始水印可以從圖像中提取旋轉置亂后的水印信息經過逆運算得到，但是前提是必須知道向量ν→的結構，因此可以說，向量ν→是水印算法中的一個密鑰。

以下是置亂算法的運行結果，其中(a)圖為水印“HUST”的原圖，(b)為旋轉后的圖像，(c)為旋轉置亂后的圖像。

圖5 數字水印旋轉置亂后的實驗結果

由圖5可見，旋轉置亂后的圖像模糊不清，已辨別不出水印圖像。

圖6為提取出的未受攻擊的水印圖像經GEMMER算法的逆變換后的效果圖，圖6(a)為提取的水印圖像，圖6(b)、6(c)分別為經置亂逆變換和旋轉逆變換的效果圖。

圖6 基于GEMMER置亂的效果圖

4 結束語

置亂技術的優劣直接影響著數字水印嵌入提取的效果，因而如何快速、高效地將數字圖像置亂成雜亂無章的圖像早已成為一個重要的研究課題。GEMMER算法經實驗證明，它較之以前的算法有以下優點:

1)在經了置換和旋轉逆變換后，還原了圖像，具有良好的周期性;

2)置亂后的圖像的能量也較集中地分布;

3)結合以上兩點，圖像在旋轉之后再進行置亂，水印圖像的能量就能實現較均勻的分布，從而達到水印的保密性大大提高的目的。

［1］Petitcolas F A P，Anderson R J，Kuhn M G.Information hiding—a survey［C］.Proceedings of the IEEE［A］.1999，87(7):1062 －1077.

［2］丁瑋，齊東旭.信息科學與微電子技術［M］.北京:中國科學技術出版社，1998:309－311.

［3］徐桂芳，曹敏謙著.純幻方的構造原理與方法［M］.西安:西安交通大學出版社，1994:78－95.

［4］尹康康，石教英，潘志庚.一種魯棒性好的圖像水印算法［J］.軟件學報，2007，12(5):668－676.

［5］易開祥，石教英.自適應二維數字水印系統［J］.中國圖象圖形學報，2008，6(5):444－449.