具有可變抽樣區(qū)間的Poisson INAR(1)CUSUM控制圖

郭新俊，朱永忠，張 艷

0 引言

控制圖作為一種重要的統(tǒng)計過程控制工具，被廣泛應(yīng)用于實施過程控制，以改進(jìn)產(chǎn)品質(zhì)量。但常規(guī)控制圖的一個基本假設(shè)前提是觀測值彼此獨(dú)立，而往往在現(xiàn)實中所采集的數(shù)據(jù)會存在自相關(guān)現(xiàn)象很難滿足獨(dú)立性假設(shè)。為了處理自相關(guān)數(shù)據(jù)，我們采用取整的自回歸滑動平均過程模型。早在1985年，Mckenzie[1]提出了一個取非整的ARMA模型（INARMA）。因為對于標(biāo)準(zhǔn)的一階自回歸模型AR（1），一個取非整的INAR（1）模型是很接近它的，所以在2007年，Weib[2]提出了一個c-chart，一個滑動平均控制圖和帶著兩個特殊條件的控制圖去監(jiān)測這樣的過程。但是，幾種相似的結(jié)果顯示它們都沒有表現(xiàn)出較好的監(jiān)測效果。直到2009年，Weiss和Testik[3]研究了一個全新的累積和控制圖Poisson INAR(1)CUSUM，完全基于Poisson INAR(1)模型，能夠很好地監(jiān)測來自INAR(1)過程的數(shù)據(jù)。而這類常規(guī)的控制圖都是假定抽樣區(qū)間和樣本容量都固定不變，它不利于及時發(fā)現(xiàn)過程的變化，特別是過程較小的變化，于是Reynolds et al[4]提出了具有變化抽樣區(qū)間的Shewhart控制圖，并由此形成了動態(tài)控制圖這一新的領(lǐng)域，之后很多學(xué)者研究了動態(tài)的累積和控制圖[5]，指數(shù)加權(quán)滑動平均控制圖[6]等。本文擬在Weiss和Testik[3]的累積和控制圖Poisson INAR(1)CUSUM的基礎(chǔ)上進(jìn)行變化的樣本區(qū)間設(shè)計，即不再假定樣本區(qū)間固定而是根據(jù)當(dāng)前樣本點落入的區(qū)域從而決定采用相應(yīng)的變化的樣本區(qū)間[7][8]。利用馬爾科夫鏈方法計算的數(shù)據(jù)判斷，與FSI圖相比是否減少了過程的平均報警時間，從而有效地提高生產(chǎn)效率。

1 Poisson INAR(1)CUSUM控制圖的描述

1.1 INAR(1)模型

McKenzie[1]早在1985年就給出了第一個INARMA和INAR(1)模型

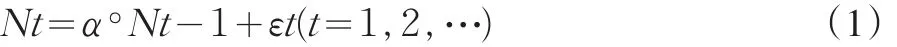
其中，Nt為離散型隨機(jī)變量，α∈(0,1)，°為減弱算子，εt是獨(dú)立同分布的隨機(jī)變量，減弱算子與εt都是相互獨(dú)立的，并且εt在每個t時刻與Nt-1,Nt-2,...都是獨(dú)立的。方程（1）中的INAR(1)模型在現(xiàn)實中有著廣泛的應(yīng)用[2]。

方程（1）中的INAR(1)過程模型是一個齊次馬爾科夫鏈。顯然，零初值是固定的。再者，此模型可適用于幾種邊緣分布，包括二項分布和泊松分布等。下面，我們只考慮泊松分布的情形——設(shè)定Nt是帶有參數(shù)λ＞0的泊松分布且 P(Nt=k)=e-λ(λkk!)；k=0,1,...。

1.2 Poisson INAR(1)CUSUM控制圖

在方程（1）中，若εt是獨(dú)立同分布的隨機(jī)變量且服從參數(shù)為λ(1-α)的泊松分布，Nt為服從參數(shù)λ＞0的泊松分布的離散型隨機(jī)變量即 P(Nt=k)=e-λ(λkk!)，k=0,1,...。那么方程（1）被稱作Poisson INAR(1)模型。

在實際應(yīng)用中可能會有很多原因使統(tǒng)計過程失控。比如Nt和εt的均值或方差可能會從受控狀態(tài)中的某個值變成失控狀態(tài)的另一個值。很多控制圖都能用來監(jiān)測Nt在過程中均值的改變，由于多樣累積和控制圖在較小和中等參數(shù)漂移監(jiān)測中的優(yōu)越性[9]，在此選用多樣累積和控制圖。Christian H Weib和Murat Caner Testik[3]在2009年提出了一個單邊的Poisson INAR(1)累計和控制圖（受控時μ=λ0）：

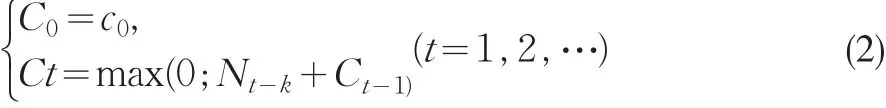
這里，c0≥0是初值，k≥λ0是信念值。過程被認(rèn)為是受控的，只有當(dāng)Ct≥h時過程發(fā)出警報進(jìn)入失控階段，其中h＞0為控制線。盡管通常情況下取初值c0=0，但是當(dāng)取c0≥0時，在監(jiān)測過程失控時更加靈敏。而k的作用是在受控階段阻止控制圖向控制線靠近，能夠及時地調(diào)整自身的取值使之對控制過程中均值漂移更加敏感

2 Poisson INAR(1)CUSUM控制圖的動態(tài)設(shè)計

2.1 動態(tài)控制圖的描述

動態(tài)控制圖[10]是指下一個樣本的抽樣區(qū)間或樣本容量依賴于現(xiàn)實樣本點統(tǒng)計量的控制圖。控制圖的動態(tài)設(shè)計一般有可變抽樣區(qū)間（Variable Sampling Interval,VSI),可變樣本容量（Variable Sample Size,VSS)及可變樣本容量和抽樣區(qū)間（VSSI)這三種情況。其主要思想為：在控制圖的中心限和控制限之間加上警戒限，將中心限與警戒限之間的區(qū)域稱為中心域，警戒限與控制限之間的區(qū)域稱為警戒域。如果現(xiàn)時樣本點統(tǒng)計量位于中心域，則表明其后的點超出控制限的可能性較小，這時可等待較長的時間再去抽取下一個樣本，且下一個樣本的樣本容量可以較小；反之，若現(xiàn)實樣本點統(tǒng)計量位于警戒域內(nèi)，這表明其后的點很有可能超出控制限，為了能盡快的發(fā)現(xiàn)過程的偏移，應(yīng)等待較短的時間去抽取下一個樣本，且其樣本容量應(yīng)該較大，也就是說下一個樣本的抽樣區(qū)間和樣本容量的大小取決于現(xiàn)實樣本點統(tǒng)計量的大小。一般只取兩個抽樣區(qū)間長度 d1，d2，和兩個樣本容量 n1，n2，其中 d1＞d2，n1＜n2。當(dāng)現(xiàn)時樣本點統(tǒng)計量位于中心域時，選取樣本容量n1和抽樣區(qū)間d1；當(dāng)其位于警戒域時，選用樣本容量n2和抽樣區(qū)間d2；若其超出警戒限，則發(fā)出報警信號，過程失控。

2.2 VSIPoisson INAR(1)CUSUM控制圖

早在上個世紀(jì)80年代，Reynolds[5]就一直在專注研究關(guān)于帶有變化的樣本容量或抽樣區(qū)間的控制圖，其中對累積和控制圖的研究占有很大比重。Reynolds和Arnold[5]在1990年給出了一個單邊的（正向的)VSICUSUM控制圖。

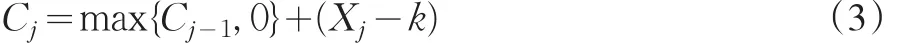
這個控制圖有效地克服了以往的抽樣區(qū)間是固定的情況下會出現(xiàn)不能及時發(fā)現(xiàn)過程較小的變化這一缺點，但是這里的隨機(jī)變量Xj一般默認(rèn)為是相互獨(dú)立的，也就是說，在實際中所觀測的數(shù)值存在自相關(guān)現(xiàn)象時，（3）式還是可能會出現(xiàn)虛報或是漏報的情況。所以我們用（2）式中定義的特殊的隨機(jī)變量Nt來替換Xj再結(jié)合Poisson INAR(1)CUSUM控制圖的優(yōu)點所得到的新的控制圖如下：

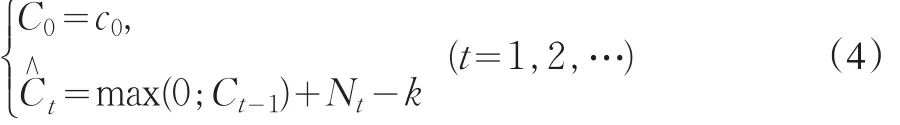
這兒，c0仍然是一個常數(shù)。而（2）中的Ct與（4）中的不同處在于Ct是將控制圖所有取負(fù)值的統(tǒng)計量全部歸零，首先會記錄那些取負(fù)值的統(tǒng)計量，然后當(dāng)代入下一組樣本計算時又將那些負(fù)值重新置為零。除去記錄取負(fù)值的統(tǒng)計量這一點以外這兩者是相同的。之所以選擇控制圖是因為那些負(fù)的統(tǒng)計量的取值很可能被用作去判別樣本區(qū)間。同樣，過程被認(rèn)為是受控的，只有當(dāng)Ct≥h時會發(fā)出警報進(jìn)入失控階段，其中h＞0為控制線。k為信念值通常由控制圖的漂移率來定，如果讓來表示μ0變到μ的幅度，那么k的最佳取值為，h的選擇則是在受控階段時使報警前的樣本數(shù)量的期望達(dá)到某個特定的值而設(shè)定。

2.3 VSIPoisson INAR(1)CUSUM控制圖ATS計算

如果使用兩個樣本區(qū)間d1和d2，用ψi表示報警前使用抽樣區(qū)間di的樣本數(shù)量，其中i=1,2。d0為第一個樣本之前的抽樣區(qū)間，也就是說d0是指從過程開始的0時刻到取第一個樣本這段時間。在許多應(yīng)用中，通常取d0=d1，其表示過程開始之后迅速地取第一個樣本。根據(jù)ATS，ANSS的定義不難得出下列等式：

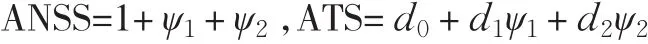
定義

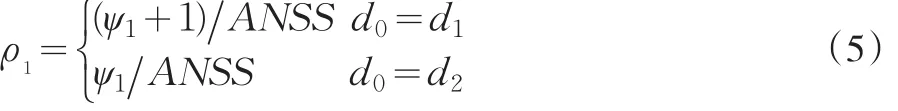
其中ρ1為樣本區(qū)間是d1的樣本數(shù)量占報警前所有樣本數(shù)量的比例。進(jìn)一步有 ATS=d?ANSS,這里d=d1ρ1+d2(1-ρ1)。

對一個可變抽樣區(qū)間控制圖來說，d可看作是平均樣本區(qū)間的長度，而在接下來討論到的固定樣本區(qū)間圖時，d就代表固定樣本區(qū)間的長度。這都是在討論單邊的情況，雙邊的控制圖統(tǒng)計量情況類似，只是要復(fù)雜一些，這里就不再說明了。

在運(yùn)用馬爾科夫鏈方法去近似計算控制圖效能值的時候，常常是將控制圖的連續(xù)區(qū)域分成若干個小區(qū)域，每個小區(qū)域都對應(yīng)著一個馬爾科夫鏈，其中有個區(qū)域稱為吸收態(tài)，表示過程失控。現(xiàn)假設(shè)將某個控制圖的連續(xù)區(qū)域C分成r個區(qū)域E1,E2,...,Er。并且每個狀態(tài)Ei相應(yīng)的去使用一個樣本區(qū)間長度。記bi表示當(dāng)控制圖的統(tǒng)計量落在區(qū)域Ei時的樣本區(qū)間，b={b1,b2,...,br}'。馬爾科夫鏈的轉(zhuǎn)移矩陣P為，這兒Q是P的子矩陣對應(yīng)于r個轉(zhuǎn)移狀態(tài)，0'是由零組成的r×1維零矩陣，1是由1組成的r×1維矩陣。

定義基礎(chǔ)矩陣M=[mij]=(I-Q)-1，這里矩陣P，Q和M都依賴于均值μ的取值。mij是轉(zhuǎn)移狀態(tài)Ej在進(jìn)入吸收態(tài)之前的過程次數(shù)的期望值。用ANSSi表示在狀態(tài)Ei時的統(tǒng)計量ANSS，且 ANSS=(ANSS1,ANSS2,...,ANSSr)'。因為在馬爾科夫鏈的一個狀態(tài)轉(zhuǎn)移發(fā)生時只取一個樣本，所以有一個多樣累積和控制圖的ANSS的取值完全依賴于參數(shù)k和h，所以無論是可變樣本區(qū)間的累積和控制圖還是固定樣本區(qū)間的累積和控制圖，如果它們有相同的k值和h值，那么這兩個控制圖有相同的ANSS值。同樣，用ATSi表示在狀態(tài)Ei時的統(tǒng)計量ATS，d0=bi，并且過程的均值是常數(shù)，則有若 d0≠bi時，有 ATS=ATSi+d0-bi。

3 比較分析

衡量控制圖性能的指標(biāo)是過程運(yùn)行到出現(xiàn)錯誤信號報警所用的時間，如果N代表報警時所運(yùn)行的樣本數(shù)量，那么固定樣本區(qū)間控制圖的報警時間則是由N和固定的樣本區(qū)間長度共同決定。所以對固定樣本區(qū)間控制圖來說，刻畫報警時間的大小就可以簡單的去刻畫N的大小。在質(zhì)量控制學(xué)中，N被稱作運(yùn)行長度。所以它的期望值平均運(yùn)行長度ARL通常被用來衡量固定樣本區(qū)間控制圖的性能。然而在變化的樣本區(qū)間控制圖中，由于抽樣區(qū)間不固定所以報警時間不能單一的由N去描述，那么只能去直接計算報警時間。同樣它的期望值定義為ATS，由于ARL關(guān)系到兩個量所以在可變的抽樣區(qū)間控制圖中我們定義報警時的樣本數(shù)量的期望值為ANSS，它代替了固定抽樣區(qū)間控制圖的ARL。例如，定義受控階段時的ANSS為500或者ATS為250小時，則意味著在受控狀態(tài)下平均運(yùn)行每500個樣本就會出現(xiàn)一次錯誤警報或者平均運(yùn)行每250小時就會出現(xiàn)一次錯誤警報。

控制圖應(yīng)在同一條件下進(jìn)行比較，換言之，當(dāng)過程處于受控狀態(tài)時，它們應(yīng)有相同的平均報警時間ATS。只要VSI控制圖和FSI控制圖有相同的n,h和k值，它們就具有相同的ANSS；也就是說，改變控制圖的抽樣區(qū)間并不改變它的ANSS。當(dāng) μ=μ0時，固定k和h。

選擇合適的警戒限和可變抽樣區(qū)間d1和d2，使得VSI控制圖和FSI控制圖有相同的平均抽樣區(qū)間，此時它們具有相同的平均報警時間ATS。分別計算當(dāng)μ≠μ0時兩個控制圖的ATS，ATS越小，控制圖的效率就越高。

在研究累積和控制圖性能時，我們通常將h和k的值均取整并且讓它們成對出現(xiàn)，如表1所給出的，而當(dāng)k的值接近λ0時控制圖的效果將更加明顯。不難看出無論是固定區(qū)間的FSIPoisson INAR(1)CUSUM亦或是可變樣本區(qū)間的VSIPoisson INAR(1)CUSUM，它們的ATS取值均受到參數(shù)α的影響。再者，對于參數(shù)c0來說，當(dāng)c0＞0時二者的統(tǒng)計量取值總比c0為零時的取值要小一些。而對于以上所有參數(shù)恒定的情況下，VSI圖的值比FSI圖的值要小，即可說明可變抽樣區(qū)間控制圖比固定樣本區(qū)間控制圖更加靈敏。

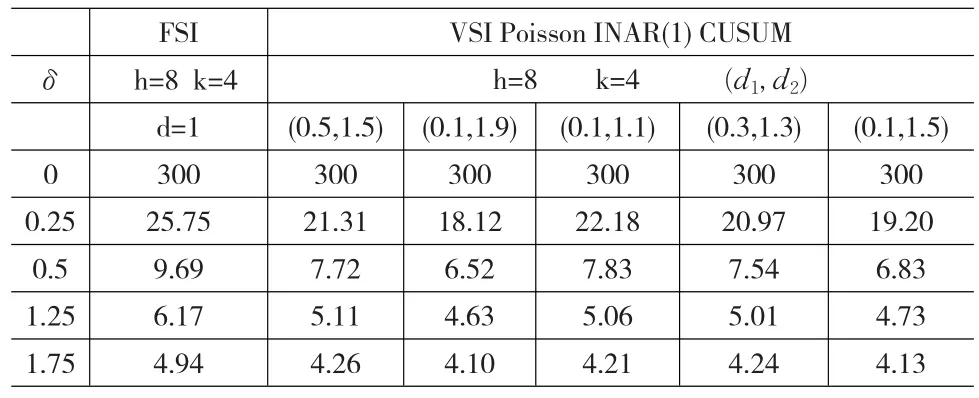
表2 帶有幾組不同區(qū)間的VSI圖和固定區(qū)間的FSI圖的ATS值

對于表2，我們是將FSIPoisson INAR(1)CUSUM的樣本區(qū)間取為d=1，而對VSIPoisson INAR(1)CUSUM的兩個不同的抽樣區(qū)間(d1,d2)分別取不同的組合，其中有兩組是關(guān)于d=1對稱的，而另外三組關(guān)于d=1不對稱的。由表可看出，對VSI無論是否取關(guān)于d=1對稱的抽樣區(qū)間的ATS值都要比FSI的相應(yīng)的值要小。早在1989年，Reynolds就提出過這樣的理論：d1的取值要盡可能的小，言下可讓d2在一定的范圍內(nèi)盡可能取大一些，但不能無限大，畢竟要受到ρ1等參數(shù)的影響。從表中也可看出，對于那三組不關(guān)于d=1的抽樣區(qū)間(d1,d2)，總是d1與d2相差最大的那組（0.1,1.5）的效果最好。而在多數(shù)情況下，通常取關(guān)于d對稱的d1與d2的值能使控制圖達(dá)到最優(yōu)效果，正如表中的兩組關(guān)于d=1對稱的d1與d2的取值，此時VSIPoisson INAR(1)CUSUM的效果最佳。

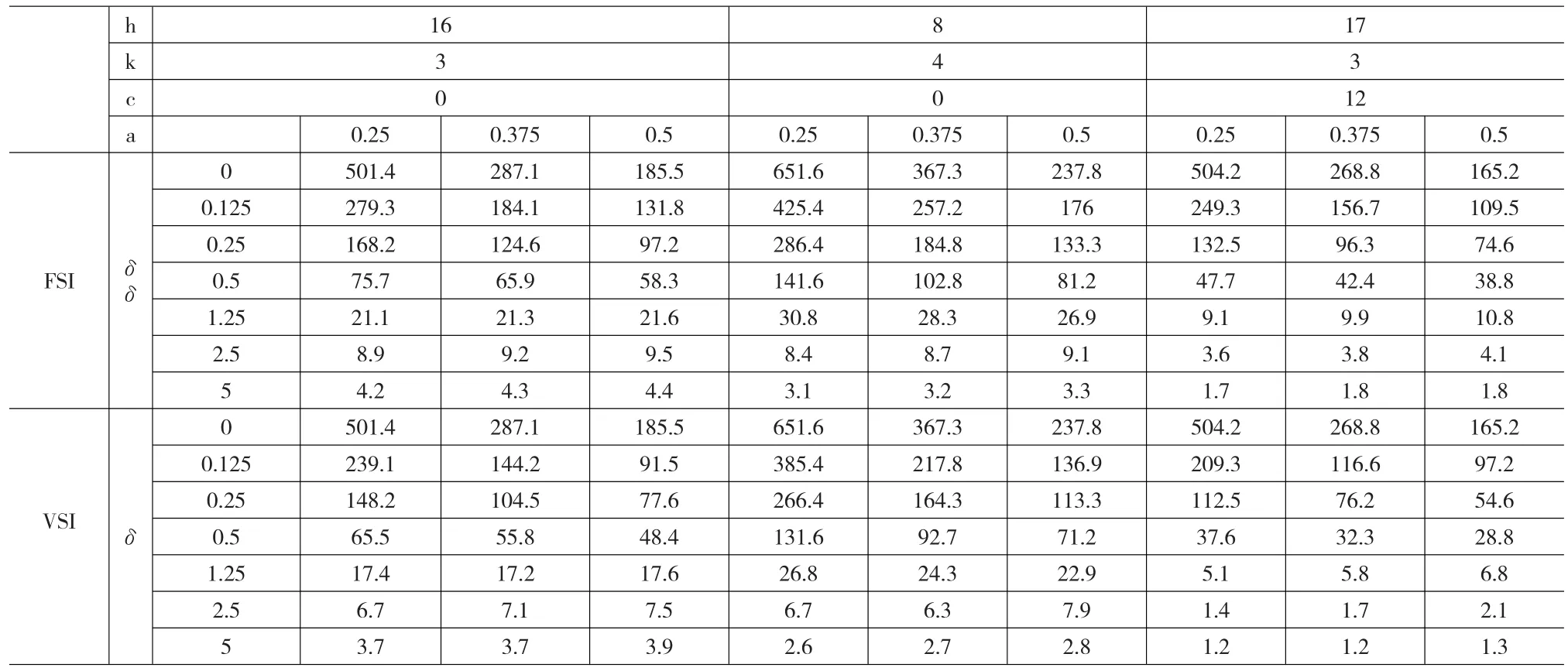
表1 帶有不同k和h值的單邊FSI圖和VSI圖在穩(wěn)態(tài)時的ATS取值

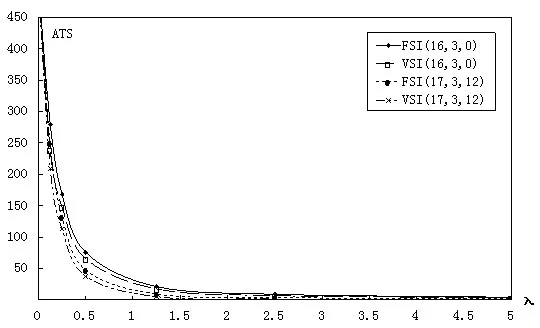
圖1 帶著相同均值漂移率的FSI和VSI的ATS值比較

圖1 中共有四條線段，其中參數(shù)（h,k,c0）為（16,3,0）的FSI圖和VSI圖以及參數(shù)為（17,3,12）的兩種控制圖的比較，很明顯當(dāng)參數(shù)相同時VSI的線段要比FSI的略低；再者，無論是FSI圖還是VSI圖，c0值較大的控制圖相應(yīng)的ATS值小。

4 結(jié)論

由于在實踐中所采集的數(shù)據(jù)通常具有自相關(guān)性，而多樣累積和控制圖在較小和中等參數(shù)漂移監(jiān)測中有優(yōu)越性，所以使用多樣累積和控制圖通過一個一階泊松取整的自回歸滑動平均過程模型（定義為Poisson INAR(1))來監(jiān)測，并且對其進(jìn)行可變抽樣區(qū)間設(shè)計。從文中可看出在參數(shù)大小相同的條件下，VSI圖的ATS值總是比FSI圖要小一些，也就是說無論在受控亦或是失控條件下，VSI圖都要比FSI圖靈敏。但就對VSI圖而言，考慮它的抽樣區(qū)間的組合，一般來說區(qū)間稍長的組合性能將更好一些。所以可變抽樣區(qū)間的累積和控制圖VSIPoisson INAR(1)CUSUM更加容易投入到實際生產(chǎn)或過程中去。

[1]McKenzie,Ed.A Traditional Interpretation of the Forecasts of Season?ally Differenced ARIMA Processes[Z].North-Holland,Amsterdam,1985.

[2]Weiss,C.H.Controlling Correlated Processes of Poisson Counts[J].Quality Reliability Engineering International,2007,23(6).

[3]Christian HWeib.Murat Caner Testik,CUSUMMonitoringof First-Or?der Integer-Valued Autoregressive Processes of Poisson Counts[J].Journal of Quality Technology,2009,41(4).

[4]Reynolds Jr.,M.R.,Arnold,J.C.X-bar Charts with Variable Sampling Intervals[J].Technometrics，1988,30(2).

[5]Reynolds Jr.,M.R.,Arnold,J.C.CUSUM Charts with Variable Sampling Intervals[J].Technometrics，1990,(32).

[6]Accucci M S,Amin R W,Lucas J M.Exponentially Moving Average Control Schemes with Variable Sampling Intervals[J].Communications in Statiatics-Simulation and Computation,1992,21(3).

[7]Yunzhao Luo,Zhonghua Li,Zhaojun Wang.Adaptive CUSUM Control Chart with Variable Sampling Intervals[J].Computational Statistics and Data Analysis,2009,(53).

[8]張維銘.可變抽樣區(qū)間的單邊控制圖[J].數(shù)理統(tǒng)計與管理，2002,6（21）.

[9]濮曉龍.關(guān)于累積和（CUSUM)檢驗的改進(jìn)[J].應(yīng)用數(shù)學(xué)學(xué)報，2003,2（26）.

[10]吉明明.具有可變抽樣區(qū)間的二維EWMA控制圖[J].系統(tǒng)工程理論與實踐，2007,9（9).