信用風(fēng)險(xiǎn)管理中損失分布法與價(jià)值分布法的模擬比較
朱春生,易榮華,劉家鵬
0 引言
隨著信用風(fēng)險(xiǎn)管理理論的創(chuàng)新和計(jì)算機(jī)技術(shù)的運(yùn)用,現(xiàn)代信用風(fēng)險(xiǎn)管理正迅速朝著信用風(fēng)險(xiǎn)被科學(xué)地量化的方向發(fā)展,現(xiàn)代商業(yè)銀行積極探索并正在積極推行的這種管理理念與方法,最終導(dǎo)致了以?xún)?nèi)部評(píng)級(jí)法(IRB)為重要內(nèi)容的新巴塞爾協(xié)議[1]的產(chǎn)生,而新巴塞爾協(xié)議又必將加快這一管理理念在全球范圍內(nèi)的推廣。
信用風(fēng)險(xiǎn)模型最重要的輸出是估計(jì)組合的風(fēng)險(xiǎn)度量VaR或ES,在此基礎(chǔ)上計(jì)算一定時(shí)間跨度的經(jīng)濟(jì)資本。經(jīng)濟(jì)資本為組合損失分布的α分位數(shù)與期望值之差,其中α為保持一定信用評(píng)級(jí)所必須的置信水平。如評(píng)級(jí)AA級(jí)的銀行α一般為99.99%,評(píng)級(jí)AA級(jí)的銀行α一般為99.9%。因此,得到信用(損失)分布是信用風(fēng)險(xiǎn)模型的關(guān)鍵。信用風(fēng)險(xiǎn)的兩種定義,得到信用損失分布的方法也有兩種。一種是只考慮違約情況的損失分布法;另一種是考慮信用遷移的價(jià)值分布法。
損失分布法也稱(chēng)為違約模型(DM)[2],只考慮了違約風(fēng)險(xiǎn),即只計(jì)算風(fēng)險(xiǎn)資產(chǎn)違約帶來(lái)的損失,CreditRisk+模型是典型的違約模型[3]。而實(shí)際上隨著時(shí)間的推進(jìn),風(fēng)險(xiǎn)資產(chǎn)的信用狀況不斷地變化。資產(chǎn)信用狀況的變化同樣也引起資產(chǎn)價(jià)值地變化,這種由于資產(chǎn)信用的遷移引起的資產(chǎn)價(jià)值的波動(dòng)稱(chēng)為信用遷移風(fēng)險(xiǎn)。貸款違約給銀行帶來(lái)?yè)p失,是現(xiàn)實(shí)的風(fēng)險(xiǎn),而信用狀況降低是潛在的風(fēng)險(xiǎn),同樣不可忽視。
價(jià)值分布法也稱(chēng)為盯市模型(MTM)[4]。價(jià)值分布法不但考慮違約帶來(lái)的損失,同時(shí)也考慮信用遷移帶來(lái)的價(jià)值波動(dòng)。單純考慮損失不能準(zhǔn)確地反映組合的風(fēng)險(xiǎn),因此信用計(jì)算整個(gè)組合的價(jià)值狀況,得出組合的價(jià)值分布,從而計(jì)算相應(yīng)的風(fēng)險(xiǎn)。J.P.摩根的Credit Metrics[4]是典型的盯市模型.遲國(guó)泰,董賀超,劉艷萍等開(kāi)發(fā)了基于信用風(fēng)險(xiǎn)遷移的組合收益與組合風(fēng)險(xiǎn)計(jì)量模型[5]。
相關(guān)領(lǐng)域的學(xué)者對(duì)目前國(guó)際上主要的信用風(fēng)險(xiǎn)度量模型和管理方法進(jìn)行了比較[6],從理論基礎(chǔ)和技術(shù)方法的角度研究模型之間的相互關(guān)系,比較分析模型的優(yōu)缺點(diǎn)。但這些研究只限于理論風(fēng)險(xiǎn),缺乏實(shí)際的數(shù)據(jù)支撐。目前也尚沒(méi)有回答以下問(wèn)題:盯市模型和違約模型得到的風(fēng)險(xiǎn)度量到底有多大的差異?是否考慮信用遷移風(fēng)險(xiǎn)的價(jià)值分布得出的風(fēng)險(xiǎn)值一定就大?為此,本文擬構(gòu)建不同類(lèi)型的模型,利用蒙特卡羅模擬實(shí)際地得到商業(yè)銀行貸款組合的損失分布和價(jià)值分布,具體地研究比較盯市模型與違約模型的風(fēng)險(xiǎn)度量ES和VaR。
1 研究方法
由于信用風(fēng)險(xiǎn)分布的非正態(tài)性及信用風(fēng)險(xiǎn)模型的復(fù)雜性和非線(xiàn)性,即使有Vasicek這樣較為簡(jiǎn)單的信用風(fēng)險(xiǎn)單因素模型,用于信用風(fēng)險(xiǎn)組合模型計(jì)算準(zhǔn)確的VaR或ES也很難得到解析解或數(shù)值解。因此,多數(shù)情況下模型需要使用蒙特卡洛模擬方法。下面介紹產(chǎn)生信用組合損失分布的蒙特卡羅模擬方法。
1.1 基于損失分布的蒙特卡羅模擬
蒙特卡羅模擬的基本思想是重復(fù)地模擬所感研究的金融變量的隨機(jī)過(guò)程,使之包括范圍廣泛的各種可能經(jīng)濟(jì)情景,這些金融變量從事先規(guī)定的概率分布中抽取。首先,估計(jì)各信用資產(chǎn)的違約概率,以及估計(jì)債務(wù)人的違約或資產(chǎn)相關(guān)性。其次根據(jù)相關(guān)矩陣產(chǎn)生具有相關(guān)性的隨機(jī)數(shù)列,由數(shù)據(jù)數(shù)列產(chǎn)生相應(yīng)的違約事件;接著根據(jù)違約事件相應(yīng)的違約損失率計(jì)算損失;最后,根據(jù)計(jì)算要求的精度,確定重復(fù)上述步驟的次數(shù)n,并進(jìn)行模擬,得到n個(gè)不同情景下的組合損失,進(jìn)行平均即可得到模擬的信用組合損失分布。
利用蒙特卡羅方法模擬信用風(fēng)險(xiǎn)分布可分為如下幾個(gè)步驟[8]:
(1)價(jià)違約概率和違約損失
金融資產(chǎn)的違約概率可根據(jù)該資產(chǎn)的內(nèi)部風(fēng)險(xiǎn)評(píng)級(jí)確定,或者參照外部的評(píng)級(jí)機(jī)構(gòu),如標(biāo)準(zhǔn)普爾、穆迪確定的行業(yè)信用評(píng)級(jí),根據(jù)該等級(jí)的歷史違約統(tǒng)計(jì)量得到。應(yīng)該注意的是,這種違約概率是過(guò)去的違約率,而不是未來(lái)違約的預(yù)期。違約損失可以根據(jù)歷史違約數(shù)據(jù)確定。
(2)估價(jià)債務(wù)人的資產(chǎn)相關(guān)性
估計(jì)債務(wù)人的違約或資產(chǎn)相關(guān)性,其方法主要有兩種:①利用兩個(gè)債務(wù)人的資產(chǎn)波動(dòng)性及其協(xié)方差結(jié)構(gòu),在默頓模型中將資產(chǎn)的相關(guān)性與違約相關(guān)性聯(lián)系在一起,計(jì)算其聯(lián)合違約概率,再歸納出違約相關(guān)性;②如果無(wú)法確定具體的債務(wù)人之間的資產(chǎn)相關(guān)性,可以采用行業(yè)相關(guān)性代替。同行業(yè)債務(wù)人之間可用行業(yè)資產(chǎn)相關(guān)性近似,不同行業(yè)債務(wù)人之間可用行業(yè)間資產(chǎn)相關(guān)性近似。
(3)產(chǎn)生相關(guān)的違約事件
產(chǎn)生相關(guān)違約事件,分四步進(jìn)行:①產(chǎn)生正態(tài)分布分布的一系列隨機(jī)數(shù),這些隨機(jī)數(shù)是獨(dú)立的。②分解資產(chǎn)相關(guān)矩陣,把前一步中的得到獨(dú)立隨機(jī)數(shù)得到相關(guān)的資產(chǎn)價(jià)值模擬。③根據(jù)每個(gè)債務(wù)人的違約概率計(jì)算違約點(diǎn),DPi=N-1(EDPi;0,1)。其中EDPi為第①個(gè)債務(wù)人的違約概率,N(?)標(biāo)準(zhǔn)正態(tài)分布的累計(jì)分布函數(shù)。④根據(jù)模擬的資產(chǎn)價(jià)值εi與違約點(diǎn)EDPi比較,判斷是否違約。當(dāng)εi<EDPi時(shí),違約;當(dāng) εi≥EDPi時(shí),不違約。
(4)產(chǎn)生隨機(jī)違約損失
發(fā)生違約,從第一步中得到LGD的均值與標(biāo)準(zhǔn)差匹配的Bata分布中抽取隨機(jī)數(shù)。
(5)計(jì)算損失
若債務(wù)人違約,則損失L可由L=EAD×LGD,其中,EAD為債務(wù)人的違約暴露,LGD為債務(wù)人的違約損失;若債務(wù)人不發(fā)生違約,其損失為0,組合中所有資產(chǎn)損失之和就是整個(gè)組合的損失。
(6)損失分布
針對(duì)每種情景產(chǎn)生一個(gè)組合損失,重復(fù)足夠多的次數(shù)得到不同情景的組合損失。用這些組合損失模擬損失分布。圖1給出了一個(gè)具體信貸組合通過(guò)上述方法模擬出損失分布。
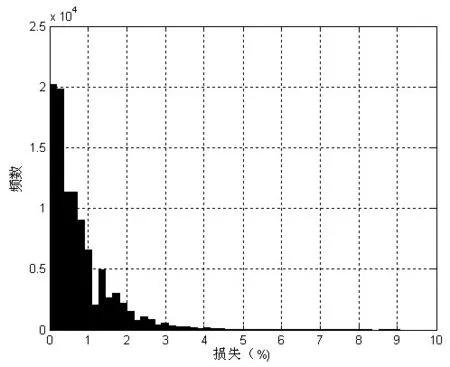
圖1 平均信用品質(zhì)組合損失分布
根據(jù)損失分布數(shù)據(jù)可以得出不同置信水平上的風(fēng)險(xiǎn)值VaR和期望短缺ES。VaR就是損失分布與不同置信水平對(duì)應(yīng)分位數(shù)上的損失值,而ES是超過(guò)相應(yīng)分位數(shù)是損失的期望值。圖2展示了所研究的信貸組合的風(fēng)險(xiǎn)狀況。
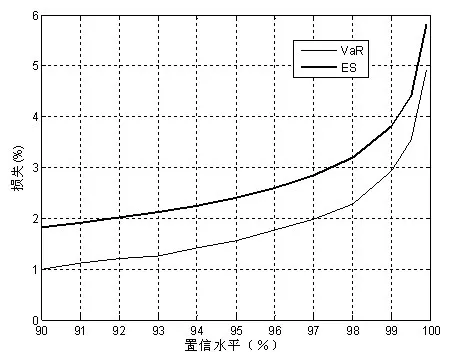
圖2 平均信用品質(zhì)組合的VaR和ES
1.2 基于價(jià)值分布的蒙特卡羅模擬
根據(jù)上面的分析與描述,我們采用蒙特卡羅模擬方法模擬大的信用風(fēng)險(xiǎn)組合的未來(lái)價(jià)值分布,并根據(jù)得到的價(jià)值分布估計(jì)相應(yīng)的風(fēng)險(xiǎn)度量,包括不同置信水平上的期望短缺ES和風(fēng)險(xiǎn)值VaR。
有關(guān)資產(chǎn)價(jià)值分布的蒙特卡羅模擬可以歸納成以下8個(gè)步驟:
(1)根據(jù)歷史數(shù)據(jù)估價(jià)信用轉(zhuǎn)移概率矩陣,實(shí)證數(shù)據(jù)參見(jiàn)相關(guān)研究[9],并計(jì)算相應(yīng)的轉(zhuǎn)換閾值,產(chǎn)生閾值矩陣。
(2)估計(jì)不同信用級(jí)別的零息貸款的期限結(jié)構(gòu)。
(3)估價(jià)貸款或貸款的信用公司資產(chǎn)收益的相關(guān)性矩陣∑,并對(duì)相關(guān)性矩陣進(jìn)行Cholesky分解∑=MMT。
(4)根據(jù)相關(guān)性矩陣的Cholesky分解產(chǎn)生多維相關(guān)性隨機(jī)序列,ε=Mη。
(5)將隨機(jī)序列和閾值矩陣進(jìn)行比較,判斷組合中各個(gè)資產(chǎn)的新的信用級(jí)別。
(6)根據(jù)新的信用級(jí)別計(jì)算各個(gè)資產(chǎn)的新的價(jià)值,求和的得到組合的價(jià)值。
(7)重復(fù)(5)、(6)多次,比如1000000次,則我們可以得到1000000個(gè)可能的未來(lái)資產(chǎn)組合價(jià)值,將之由小到大排序,形成一個(gè)一年后的可能資產(chǎn)價(jià)值樣本分布。
(8)根據(jù)價(jià)值分布計(jì)算風(fēng)險(xiǎn)值(VaR)和期望短缺(ES)。
圖3是給出一個(gè)特定組合的模擬結(jié)果,根據(jù)上述步驟得出的價(jià)值分布。
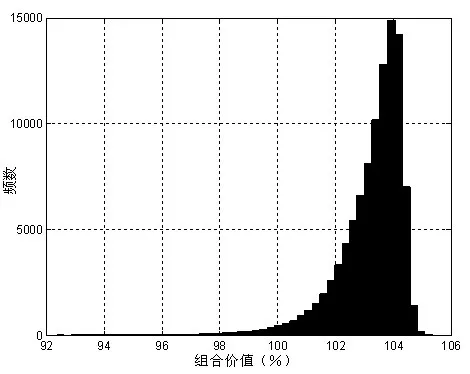
圖3 普通信用品質(zhì)組合的價(jià)值分布
圖3 是向左拖出尾部,圖4是向右拖出尾部,這并不矛盾,因?yàn)閳D4顯示的是損失分布,上圖是價(jià)值分布,所以分布特征基本是一致的,只是存在數(shù)量差異。
2 結(jié)果與分析
為了進(jìn)行比較基于價(jià)值分布和基于損失分布的風(fēng)險(xiǎn)度量,我們研究不同信用品質(zhì)的資產(chǎn)組合的風(fēng)險(xiǎn)值VaR和期望短期ES,它們是有效和常用的風(fēng)險(xiǎn)度量。這里選定高信用品質(zhì)、評(píng)價(jià)信用品質(zhì)、低信用品質(zhì)的三種貸款組合,(見(jiàn)表1)。三種信用品質(zhì)貸款組合都包括100項(xiàng)投資級(jí)貸款,組合的貸款總額96 000 000元平均貸款年限4.3年。高信用品質(zhì)貸款組合全部為投資級(jí)貸款;一般信用品質(zhì)組合包括各種信用級(jí)別的貸款;低信用品質(zhì)貸款組合全部來(lái)自投機(jī)級(jí)貸款。
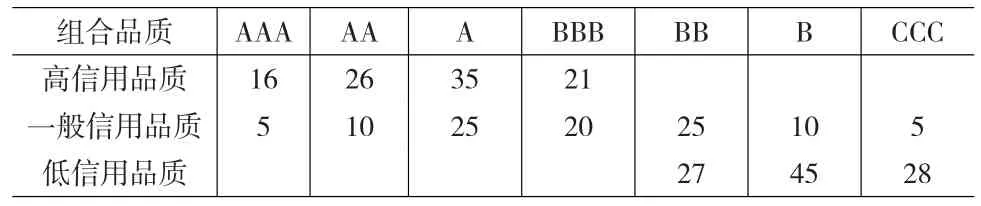
表1 三種貸款組合的信用品質(zhì)構(gòu)成
我們分別計(jì)算了上述三種不同信用品質(zhì)組合的基于損失分布的VaR和ES以及基于價(jià)值分布的VaR和ES,具體結(jié)果見(jiàn)表2。
從表2可以看出,考慮遷移風(fēng)險(xiǎn)的價(jià)值分布計(jì)算的風(fēng)險(xiǎn),無(wú)論是風(fēng)險(xiǎn)值(VaR)還是期望短期(ES)在各種信用質(zhì)量組合的情況下都比較接近,說(shuō)明信用風(fēng)險(xiǎn)還是以違約風(fēng)險(xiǎn)為主,信用遷移風(fēng)險(xiǎn)只所占比例與組合的風(fēng)險(xiǎn)狀況有關(guān)。對(duì)于高品質(zhì)貸款組合,考慮遷移風(fēng)險(xiǎn)后無(wú)論是ES還是VaR都有顯著增大,遷移風(fēng)險(xiǎn)所占比例較大,原因在于高信用級(jí)別的公司如果公司信用質(zhì)量改變,信用變壞的可能性更大。而一般組合的遷移風(fēng)險(xiǎn)所占比例減少,風(fēng)險(xiǎn)增加不大。而低信用品質(zhì)的高風(fēng)險(xiǎn)貸款組合,在考慮信用遷移風(fēng)險(xiǎn)的情況下總的風(fēng)險(xiǎn)反而降低。其原因在于低信用級(jí)別的公司如果公司信用質(zhì)量改變,信用變好的可能性更大,而且信用變壞的違約狀態(tài)已經(jīng)在違約風(fēng)險(xiǎn)中考慮過(guò)。這也印證了隨著時(shí)間跨度的增長(zhǎng),高信用級(jí)別的違約率增長(zhǎng)快,而低信用級(jí)別的公司的違約率增長(zhǎng)慢的現(xiàn)象。圖4給出了兩種方法計(jì)算不同信用品質(zhì)組合的ES之差。
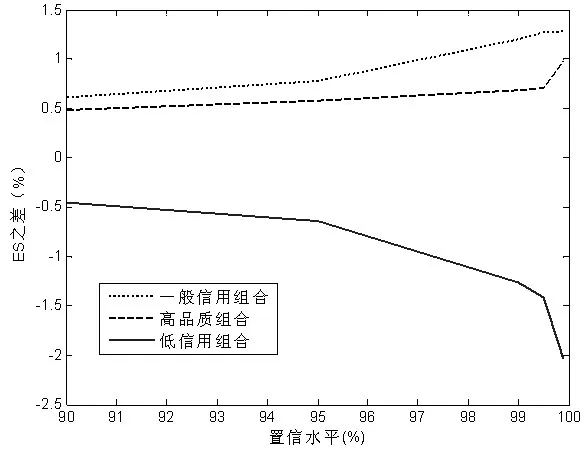
圖4 兩種方法ES風(fēng)險(xiǎn)比較
從圖4中可以看出,兩種方法大約對(duì)ES計(jì)算的風(fēng)險(xiǎn)值有1~2個(gè)百分點(diǎn)的影響,其信用遷移風(fēng)險(xiǎn)中高品質(zhì)信用組合和一般信用品質(zhì)組合是正當(dāng)影響即增加風(fēng)險(xiǎn);而對(duì)低信用品質(zhì)組合是負(fù)的影響,也就是減少風(fēng)險(xiǎn)。雖然,高品質(zhì)組合的曲線(xiàn)在一般信用組合的下面,但由于高品質(zhì)信用組合本身風(fēng)險(xiǎn)較大,信用遷移實(shí)際所帶來(lái)的影響要大些。
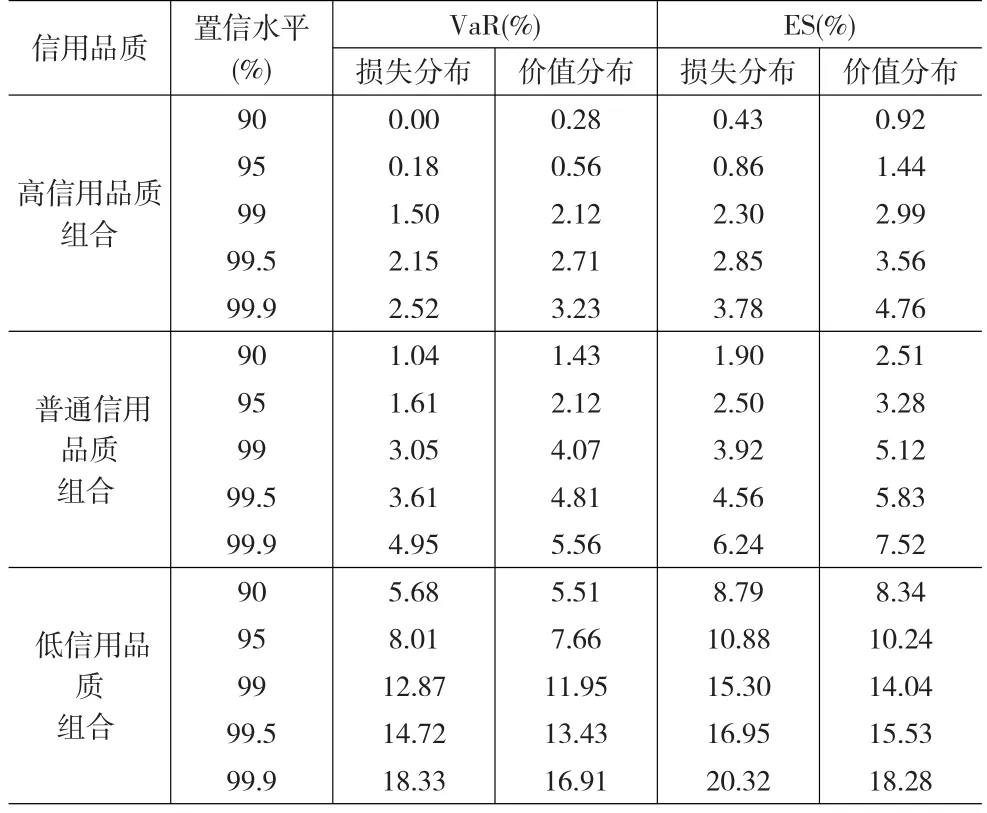
表2 價(jià)值分布和損失分布下計(jì)算的V a R和E S 的比較
3 結(jié)論
通過(guò)實(shí)際的模型計(jì)算比較相應(yīng)的風(fēng)險(xiǎn)狀況我們得出如下結(jié)論:首先,信用遷移風(fēng)險(xiǎn)對(duì)高品質(zhì)信用組合有一些一些影響,其它情況下與違約風(fēng)險(xiǎn)相比信用遷移風(fēng)險(xiǎn)影響較小,信用風(fēng)險(xiǎn)還是以違約風(fēng)險(xiǎn)為主;其次,并不是包括信用遷移風(fēng)險(xiǎn)的廣義信用風(fēng)險(xiǎn)就大,而是與資產(chǎn)組合的信用狀況相關(guān),高信用品質(zhì)的資產(chǎn)信用遷移增加風(fēng)險(xiǎn),而對(duì)低信用品質(zhì)的資產(chǎn)信用遷移減少風(fēng)險(xiǎn)。從監(jiān)管資本的角度,采用內(nèi)部評(píng)級(jí)法的銀行可以靈活運(yùn)用盯市模型(MTM)和違約模型(DM),資產(chǎn)相應(yīng)級(jí)別較高時(shí)采用基于損失分布的違約模型計(jì)算的監(jiān)管資本較低,而通過(guò)基于價(jià)值分布的盯市模型計(jì)算的經(jīng)濟(jì)資本較高;反之,當(dāng)銀行資產(chǎn)信用狀況較差是采用盯市模型計(jì)算經(jīng)濟(jì)資本會(huì)低一些。如此,恰當(dāng)?shù)夭捎貌煌哪P头椒梢缘你y行應(yīng)對(duì)巴塞爾協(xié)議的監(jiān)管時(shí)更有利一些。
[1]巴塞爾委員會(huì).統(tǒng)一資本計(jì)量和資本標(biāo)準(zhǔn)的國(guó)際協(xié)議:修訂框架[M].北京:中國(guó)金融出版社,2004.
[2]安東尼·桑德斯.信用風(fēng)險(xiǎn)度量[M].北京:機(jī)械工業(yè)出版社,2001.
[3]陳旭鳴.現(xiàn)代信用風(fēng)險(xiǎn)管理模型發(fā)展研究[J].統(tǒng)汁與決策,2008,(9).
[4]JP Morgan.CreditMetrics-Technical Document[M].New York:他和Morgan Guaranty Trust Company,1997.
[5]遲國(guó)泰,董賀超,劉艷萍.基于信用風(fēng)險(xiǎn)遷移的組合收益與組合風(fēng)險(xiǎn)計(jì)量模型[J].科研管理,2009,V30(2).
[6]沈沛龍,任若恩.現(xiàn)代信用風(fēng)險(xiǎn)管理模型和方法的比較研究[J].經(jīng)濟(jì)科學(xué),2002,(3).
[8]詹原瑞.銀行信用風(fēng)險(xiǎn)的現(xiàn)代度量與管理[M].北京:經(jīng)濟(jì)科學(xué)出版社,2004.
[9]Carty,Lea.Moody’s Rating Migration and Credit Quality Correlation,1920-1996[R].Moody’s Special Report,1997.

