偽逆矩陣的一種改進解法及其在自由網平差和擬穩平差中的應用

范國慶，楊喜平

(武漢大學測繪學院，湖北武漢430079)

偽逆矩陣的一種改進解法及其在自由網平差和擬穩平差中的應用

范國慶，楊喜平

(武漢大學測繪學院，湖北武漢430079)

提出偽逆陣的一種改進解法，該方法不但理論嚴密、計算簡單，而且解偽逆陣的公式易于編程實現，可以同時用在自由網平差和擬穩平差中，它還可以將這兩種平差結合起來對變形監測網基準點進行穩定性檢驗和分析，最后通過實際算例驗證該方法的有效性。

偽逆陣;基準點;自由網平差;穩定性分析;擬穩平差

一、引 言

自由網平差和擬穩平差的數學模型是相同的，差別在于采用不同的參考系。在平差過程中，如果沒有足夠的起始數據，就會引起誤差矩陣的系數陣列虧，這就是秩虧自由網平差。為了解決該問題，參考文獻［1］已闡述了較多的方法。在秩虧自由網平差中，需要對偽逆矩陣求逆，傳統的解法計算繁瑣、工作量大。本文根據偽逆矩陣對其解法進行改進，得到了一種解偽逆陣較簡單的公式，此公式計算簡單、易于在編程過程中實現，并且可以簡單地將自由網平差、擬穩平差和網點穩定性檢驗聯合在一起，直接計算網點的位移量。

二、偽逆陣解法的改進及其在秩虧自由網平差和擬穩平差的應用

1.秩虧自由網平差的基本原理

秩虧自由網平差的函數模型為［2-4］。

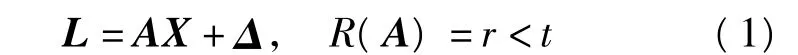
式中，A的列虧數d=t－r，隨機模型為

式(1)的誤差方程為

平差原理為

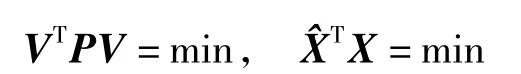
法方程為

式中，N=ATPA。

由于R(N)=R(A)=r，所以N奇異，為消除秩虧可以附加如下的約束條件

式中，R(G)=d。式(5)要滿足的條件有：①網的條件數量等于秩虧數;②GT矩陣的行跟A矩陣的行需要獨立線性。

結合式(4)和式(5)得到［5］

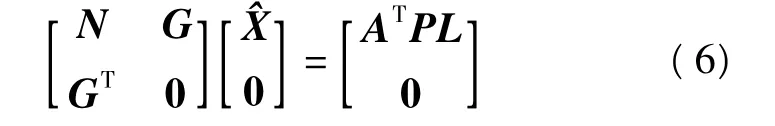
式(6)的系數矩陣的逆矩陣可以用塊矩陣表示

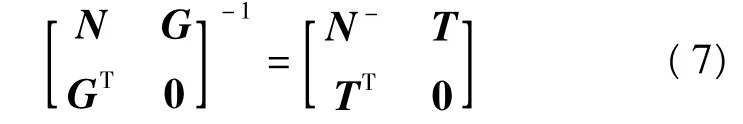
式中，N－為N的一種偽逆陣形式。

因此，未知參數求解為

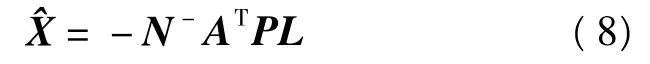
單位權方差估值仍為

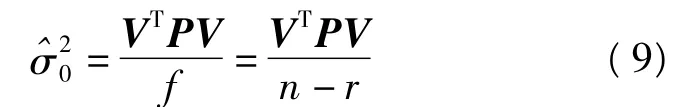
2.解偽逆陣的一種改進解法

由式(7)得出下面的等式

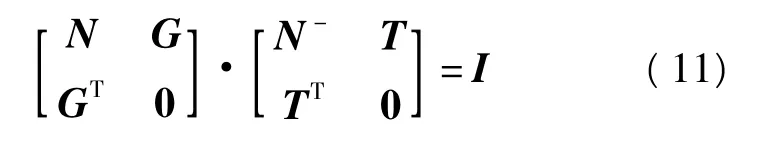
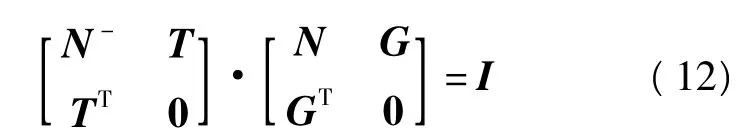
式中，I為單位陣，由式(11)可得

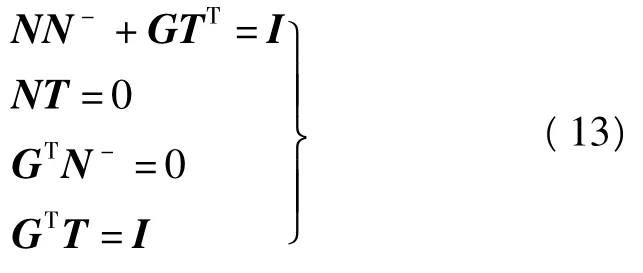
由式(12)有

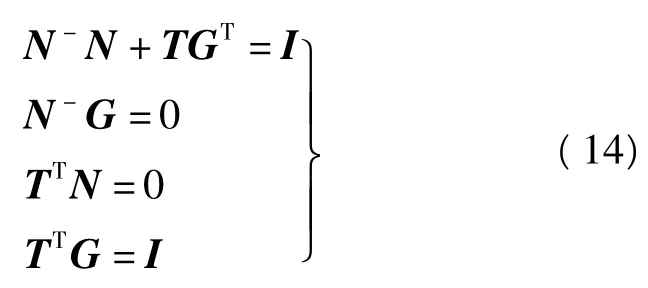
(1)計算T矩陣

由式(14)可得

將式(15)的兩邊乘以Bt，d得

若B矩陣滿足性質

則N－NB=0，求得T矩陣為

因自由網平差和擬穩平差的參考系方程系數矩陣(或稱基準轉換矩陣)滿足式(17)，所以在平差過程中，選B矩陣為參考系方程系數矩陣。

(2)計算N－矩陣

由式(13)可知

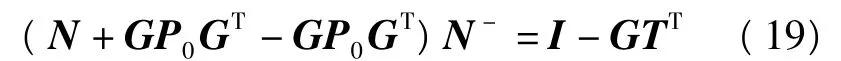
式中，P0為d×d階的矩陣，不變。

由GTN－=0，則

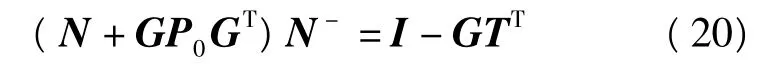
所以

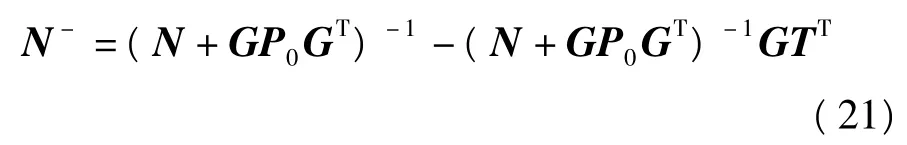
另外，由NT=0和GTT=I可知，G陣相當于

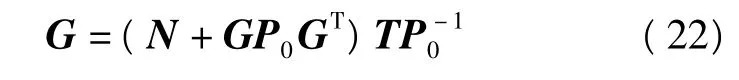
最后得到

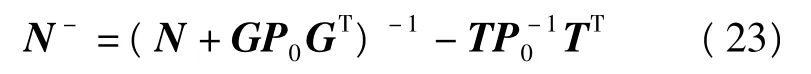
當P0=I時

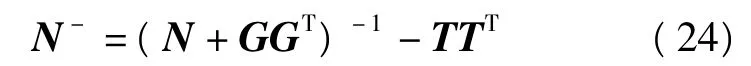
特殊的情況下，當G=B時，N－矩陣就滿足廣義逆N+矩陣，即

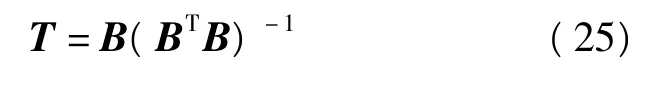
則有

實際計算中，式(23)中的P0矩陣常選為對角矩陣

有

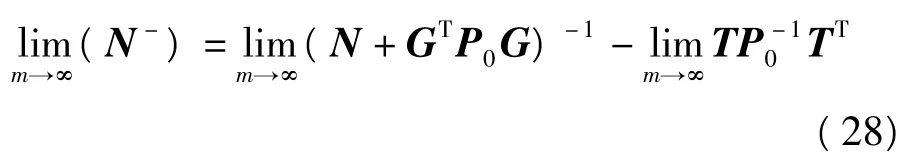
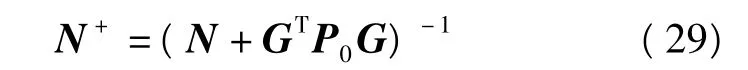
實踐證明［5］，當m≥6時，式(29)即滿足精度要求。

三、偽逆陣改進公式的應用

1.在自由網平差和擬穩平差中的應用

在自由網平差中，為了簡單運用式(29)，對高程網來說，常選

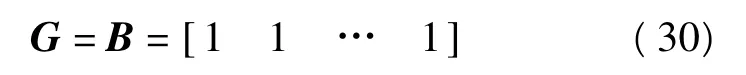
對平面測角網來說，有

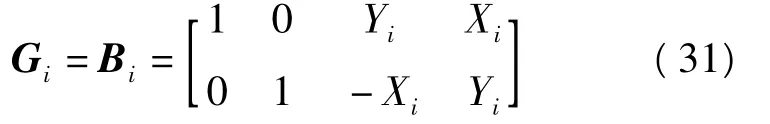
式中，i=1，2，…，n，為網點數;(Xi，Yi)相應為點的近似坐標。若是平面測邊網或平面測邊角網，則式(31)的矩陣沒有4列。

對于擬穩平差，G陣的形式跟自由網平差一致，差別在于，哪個網點是動點，G陣相應的值就為零，若點i是動點，則Gi=Bi=0。

2.聯合自由網平差和擬穩平差對網點穩定性檢驗

從理論上可知，自由網平差和擬穩平差的差別在于參考系方程系數矩陣B的選擇問題。在變形監測數據處理中，如果采用自由網平差，除了第1期外，每周期都要進行基準網點穩定性檢驗，現代測量數據處理理論具有很多方法可以發現基準網點是否穩定，如平均間隙法、穩健迭代權法、單點位移分量法等，具體的理論可以參考文獻［1，6］。本文利用上述公式，聯合自由網平差和擬穩平差對網點進行穩定性檢驗，網點穩定性檢驗采用平均間隙法，此方法的思想是：首先對兩期觀測值進行自由網平差(同近似坐標)，G矩陣的選擇如式(30)或式(31)，利用平均間隙法對網點穩定性進行檢驗之后，如果網中存在動點，將網的動點再選G矩陣，即

由于執行基準點穩定性檢驗及式(32)不可能同時計算，那么最好的解法應該是使用重復的方法計算，直到網中沒有動點為止。該方法的實現步驟如下：

1)對第i－1期基準網進行自由網平差，首先通過間接平差得到網中各點的坐標，然后把得到的坐標作為自由網平差的近似坐標。

2)在第i期，假定所有網點都是穩定點并選矩陣Gi=Bi進行自由網平差;兩期的近似坐標一致。

3)利用平均間隙法進行基準點穩定性檢驗，首先對網進行整體檢驗，看網中是否存在動點。若發現網中具有動點，則用“嘗試法”［6］將不穩定點找出來，找到動點就按照式(32)改變G矩陣，然后用新的G矩陣進行自由網平差，繼續對網點檢驗，直到沒有動點再進行下一步。

4)對網中不穩定的點運用第3)步中的G矩陣繼續進行平差處理，獲得的最后結果與擬穩平差的結果一致。

上述步驟的流程如圖1所示。

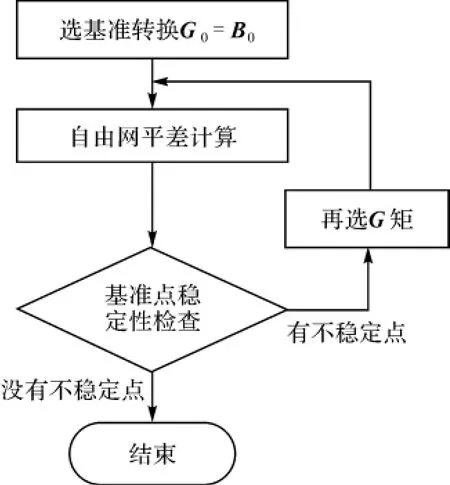
圖1 自由網平差和擬穩平差聯合的流程圖

四、算例分析

以某大壩的變形監測基準網為例，網中具有8個點，如圖2所示，該網是加密網，其中1、3、5、7點是已知點。選擇第1期和第2期的觀測數據進行試驗分析，該網每期測25個角和12條邊長，觀測數據記在表1和表2。利用VB6.0語言根據上述的步驟編制了一個結合自由網平差、擬穩平差對網點穩定性檢驗的軟件。

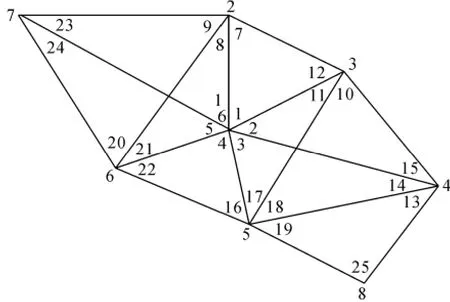
圖2 某大壩變形監測基準網

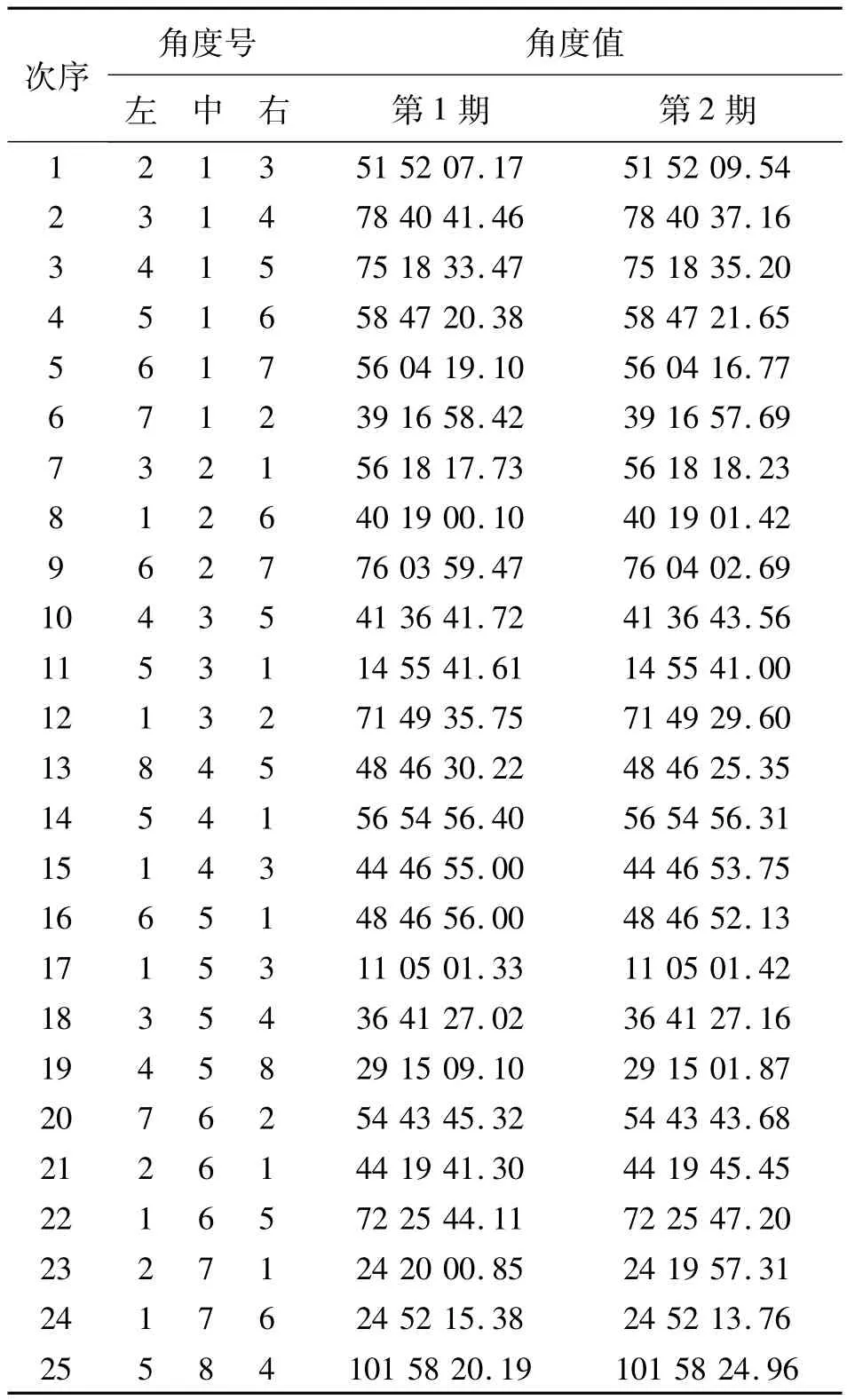
表1 兩期角度觀測值 (°'″)

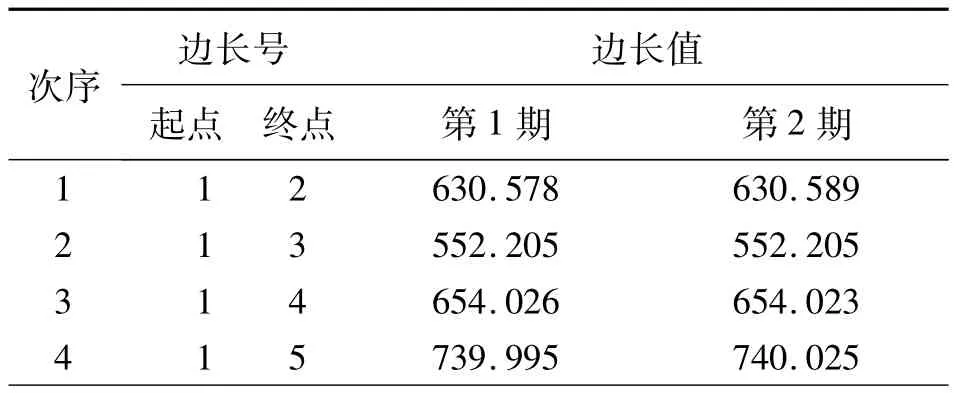
表2 兩期邊長觀測值 m

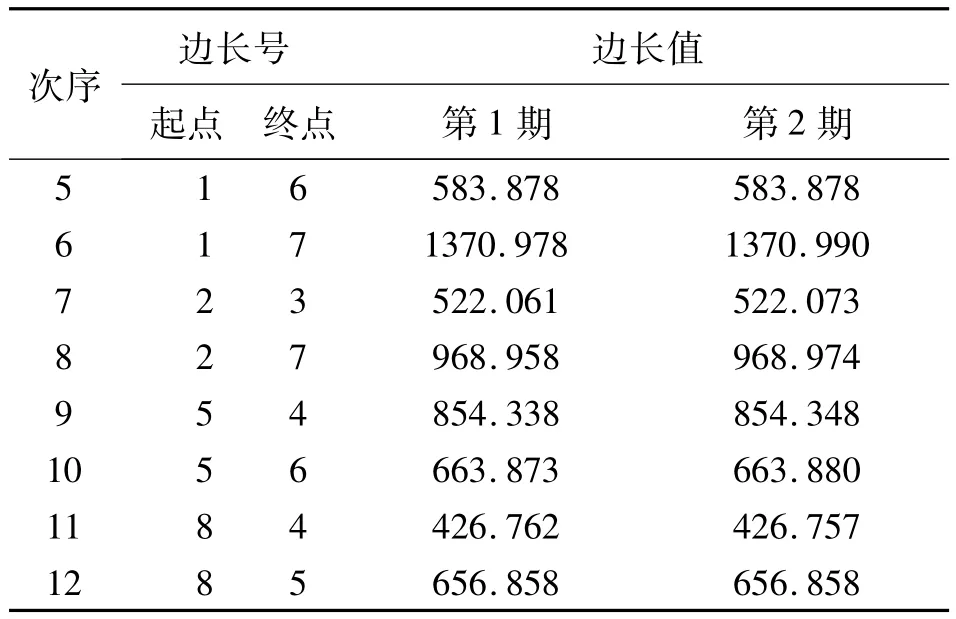
續表2 m

處理過程如下：

1)第1期的處理要憑4個已知點(1、3、5、7點)進行間接平差，其次把平差后的坐標作為第1期自由網的近似坐標(見表3)，然后對第1期觀測的數據進行自由網平差。處理過程中，運用本文的式(29)得到第1期的平差坐標見表3。

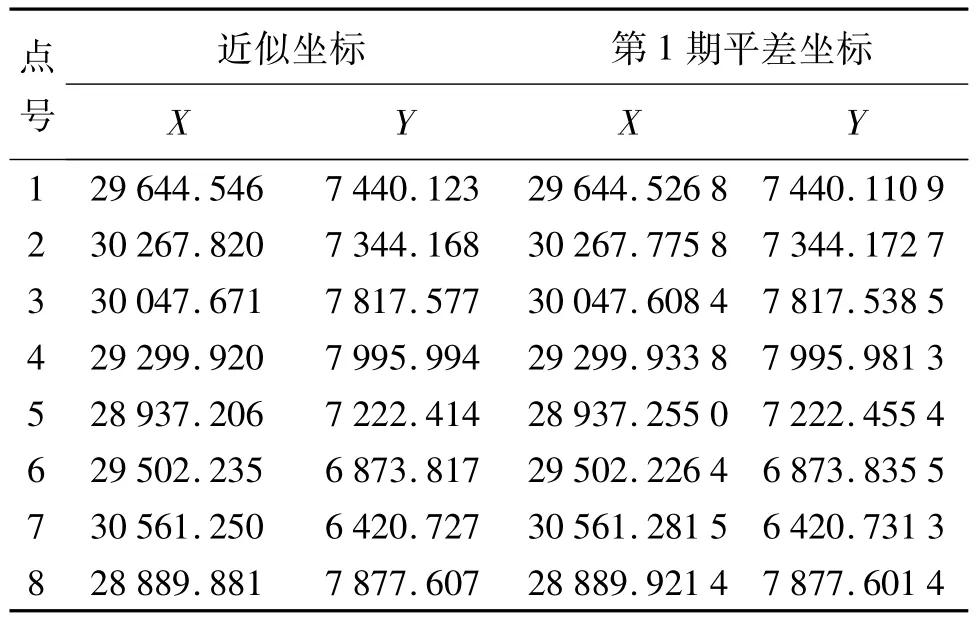
表3 網點近似坐標和第1期平差坐標 m

2)第2期自由網計算的近似坐標和第1期一致，對于G矩陣，首先認為所有網點是穩定點，則G矩陣對應為

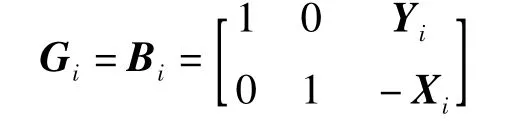
式中，i=1，2，…，8，為網點數;(Xi，Yi)為相應網點的近似坐標。進行自由網平差后得到網點平差坐標。將第2期和第1期平差后的坐標對比，獲得網點的位移量見表4。

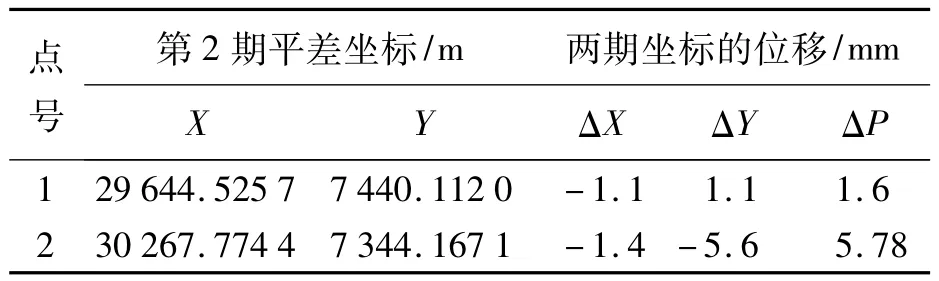
表4 網點的第2期的自由網平差坐標與網點的位移量

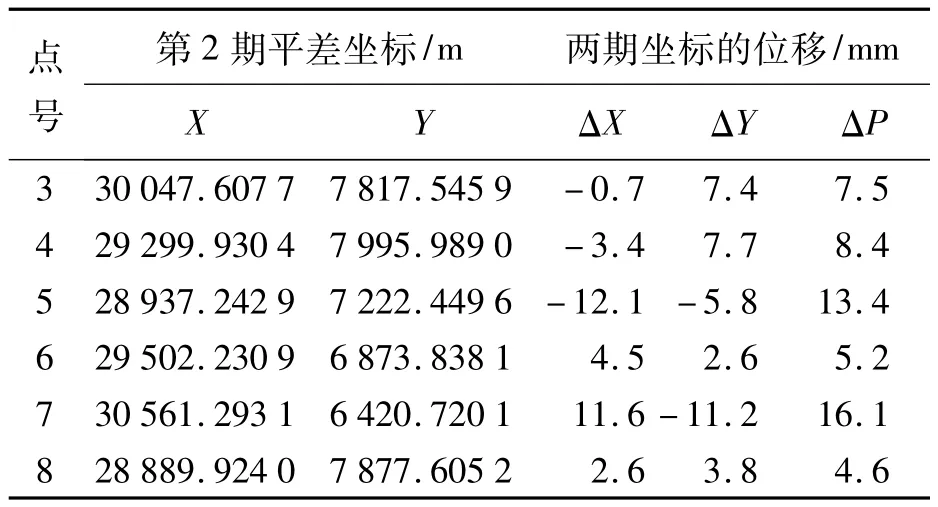
續表4

3)采用平均間隙法進行網整體檢驗是否有動點，得到統計量F=2.28。取顯著水平α=0.05，則F0.05(24，24)=1.98，由于F＞F0.05(24，24)，因此認為兩期觀測期間網中存在動點。

用平均間隙法找不穩定點要用到“嘗試法”，找到點7是動點，所以令

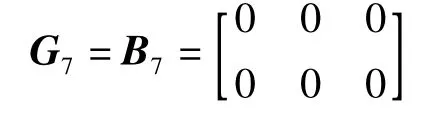
重新計算，再執行檢驗，發現點5也是動點，又令

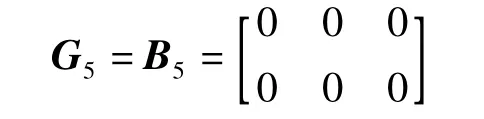
繼續計算和檢驗，獲得統計量F=0.74＜F0.05(24，20)=2.08，所以接受原假設，認為余下的各點均為穩定點，檢驗過程到此為止。

4)將新的G矩陣代入進行自由網平差，這時自由網平差就變成擬穩平差，因此獲得的結果等于擬穩平差的結果。兩期之間的新平差坐標和新位移量見表5。

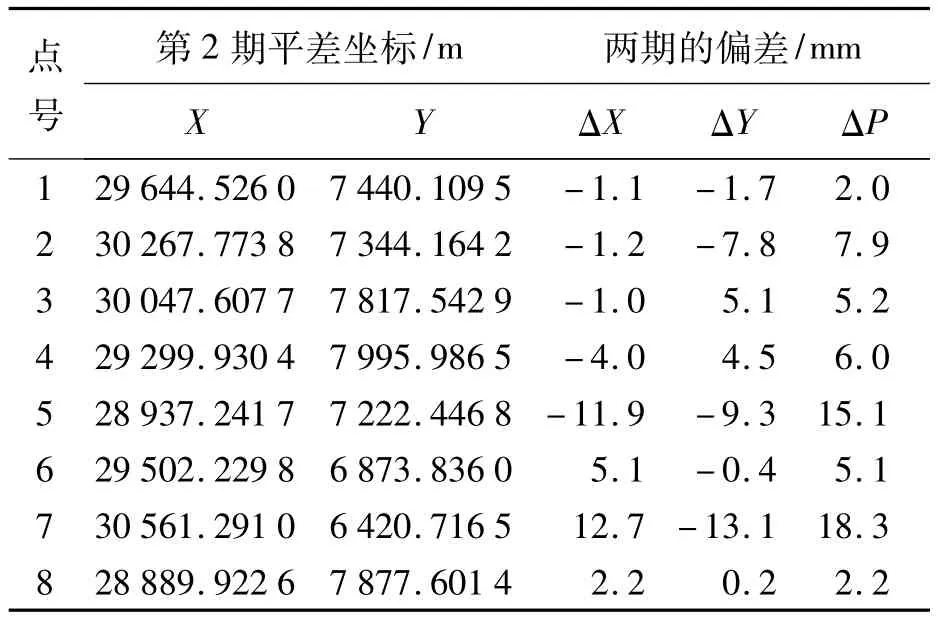
表5 網點的第2期的擬穩平差坐標與兩期位移量

用擬穩平差原理進行平差獲得的結果與上面的方法一致。

五、結 論

1)采用式(29)求解偽逆陣在自由網平差比較簡單，只通過一個公式即能得到N+矩陣。

2)根據本文提出的流程不僅能使編程過程容易實現，而且還能把變形監測基準網數據處理中的自由網平差、基準網穩定性檢驗和擬穩平差聯合起來進行處理，直接獲得網點位移量。

3)變形監測基準網在處理過程中必須進行網點穩定性檢驗，因此這種方法用于變形監測基準網是比較有效的。

［1］ 陶本藻.自由網平差與變形分析［M］.北京：測繪出版社，2001.

［2］ 黃聲享，尹暉，蔣征.變形監測數據處理［M］.武漢：武漢大學出版社，2003.

［3］ 侯建國，王騰軍.變形監測理論與應用［M］.北京：測繪出版社，2008.

［4］ 朱建軍，賀躍光，曾桌喬.變形監測的理論與方法［M］.長沙：中南大學出版社，2004.

［5］ TRAN K.自由網平差在工程測量數據處理中應用研究［D］.河內：越南河內礦業地質大學，1996.

［6］ 黃聲享.監測網的穩定性分析［J］.測繪信息與工程，2001(3)：16-18.

An Improved Pseudo-inverse Matrix of the Solution and Its Application for Free Network Adjustment and Quasi-stable Adjustment

FAN Guoqing，YANG Xiping

0494-0911(2012)09-0011-05

P207

B

2012-01-04

范國慶(1978—)男，越南人，博士生，主要研究方向為變形監測數據處理、分析與預報。