圖像的可逆水印算法研究

楊 超

（煙臺職業學院，山東 煙臺 264670）

數字水印技術的基本思路是在現今流行的數字技術產品(數字視頻、數字圖像和數字音頻等)中嵌入不可見或者微小的信息，用來證明數字產品的一些版權問題歸屬和擁有權等，信息隱藏技術包含了數字水印技術，在實際應用中，數字水印技術常被用來標注和證明產品的真實可靠性，證明是否盜版行為或者為客戶提供一些附加的產品信息[1].經通過將近20年的研究，數字水印技術已漸漸發展成熟.在目前，大多數研究者們的目光主要集中在數字圖像水印研究方面，對音頻水印的研究的關注就相對于來說比較少了.

1 可逆水印算法的優點

現代科學技術的不斷發展，水印技術也在不斷前進，可逆水印算法是在數字水印算法的基礎上形成的，但是它可以更好的填補傳統數字水印算法的缺陷.可逆水印算法為分析信號提供了更加精確的方法，它首先是把信號頻帶進行劃分，一般都是劃分為多個層次，然后進一步分解數字轉換沒有細分的高頻信號，并提取信號特征自適應選擇相應的頻帶，匹配信號譜，這樣可以改善的時頻分辨率.可逆水印算法可以在保持大小不改變的情況下，進行冗余的傳遞，是因為它保證了表示這些信息能量所需要的系數的個數的不改變，這也就是說數字水印中的信息并不是在數字圖像的分解系數組中平均分布的，同時這些系數之間又是存在著相互制約的關系的，這是一個很好的混合操作，使得傳統的攻擊——基于數理統計方法創建沒有效果.

2 圖像可逆水印算法研究

2.1 圖像的L S B算法

圖像的L S B算法的實現比較簡單，其形成水印圖片的步驟為[2]：

2.1.1 對于最初開始需要加載的水印圖像，要把它最初由10進制表示的時/空域像素值轉換成2進制表示，下面的圖1作為一個例子來展示.

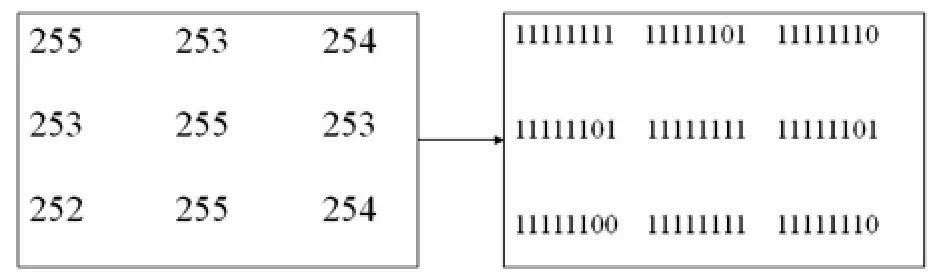
圖1

2.1.2 使用二進制秘密信息每一位的信息替換為相應的矢量數據最低有效位,假設能夠嵌入秘密信息的二進制序列[011000100],替換過程如圖2顯示了.

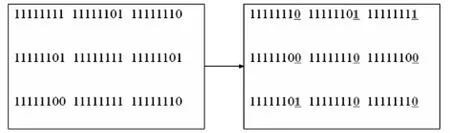
圖2

將包含機密信息的二進制數據轉換成十進制像素值,從而獲得包含機密信息的圖像,如圖3顯示.

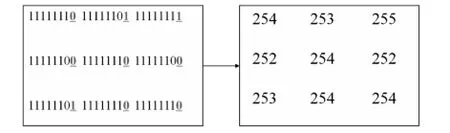
圖3

L S B算法提取水印步驟如下：

將隱藏秘密信息十進制像素轉換成二進制數據,如圖4顯示.

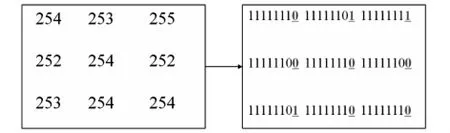
圖4

將二進制數據的最低有效位提取出來，即為秘密信息序列[011000100].如圖5所示.

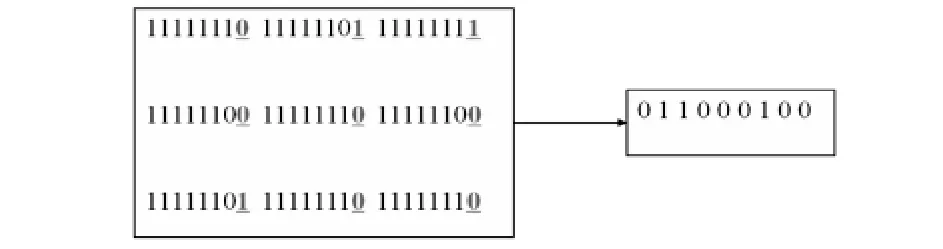
圖5

2.2 基于差分圖像的可逆水印算法

在差分圖像的基礎上建立的可逆水印算法可以實現通過預處理過程和嵌入過程,提取和恢復過程中等等來實現[3-4].

2.2.1 預處理過程

對于已經得到的差分圖像函數D（i，j），可以求出其直方圖的最高值點pm，那么pm和-pm是在差分圖像像素圖形之中出現的最大數，我們可以把這個最大數記為mpm.接下來，我們就要考察pm點在直方圖上的上下相鄰近的點(即為 pm-1、pm+1).把 pm-1、pm+1對應的直方值找出來，取其中較大者，可記為mpmn，相應的像素值(pm-1或pm+1)可記為pmn.這樣我們就可以直接地比較pm和pmn的大小，其中較大者要記為ph，對應的直方值要記為mph，相對較小者要記為pl（ph=pl+1），較小者的直方值要記為mpl.接下來我們就要考慮嵌入水印的問題，這里我們是通過移動PSNR、ph（=pl+1）和 ph+1，以及 ph+2這四點的直方值來實現的.這樣一來，我們知道的嵌入容量就為mph+mpl.

2.2.2 嵌入過程

在嵌入過程中，我們需要考慮如何把水印序列W嵌入到載體圖像I（i，j）中.為了解決這個問題，首先，我們需要通過平移把 D（i，j）差分圖像函數在點±（pl+1）和點±（ph+1）的直方值清空.如果ph的值小于或者等于差分圖像函數在某一點的像素值，我們就要把原始載體圖像中所有奇數列所對應的像素值加上2.如果-ph大于或者等于差分圖像函數在某一點的像素值，就要把原始載體圖像中所有對應的奇數列對應的像素值減去2.最后，把修改后的差分圖像函數記為 J（i，j）.

在對差分圖像函數進行修改后，就需要通過修改后的差分圖像函數的直方圖間接的修改原始的載體圖像，在其中嵌入進水印序列.首先，逐個點逐個點的查詢修改后的差分圖像J（i，j），在查詢的過程中，如果遇到某一點的像素值為±（ph+2）或者±pl，在此需要考察準備被嵌入的水印序列位.如果水印序列位為1，那么J（i，j）在這一點的值就要被修改：如果水印序列位為-pl，那么J（i，j）在這一點的值就要減去1最終變為-（pl+1），就是把初始載體圖像中的奇數列所對應的像素點減 1；如果水印序列位為 pl，那么 J（i，j）在這一點的值就要加上1變為pl+1，就是把初始載體圖像中的奇數列所對應的像素點加1；如果水印序列位為ph+2，那么J（i，j）在這一點的值就要減去1變為ph+1，就是把初始載體圖像中的奇數列所對應的像素點減1；如果水印序列位為-（ph+2），那么 J（i，j） 在這一點的值就要加上 1變為 -（ph+1），就是把初始載體圖像中的奇數列所對應的像素點加 1.而如果水印序列位為 0，那么 J（i，j）在這一點的值就不需要做任何修改.接著查詢，一直持續到 J（i，j）中第二次出現像素值±ph或±pl為止，接著依然根據水印序列位的值，進行新一輪的循環修改中.循環修改結束后，被嵌入水印后的載體圖像的奇數列Iw（i，2j+1）是可以有下面的推導得出來的：若 W（u，v）=1，J（i，j）=±ph或者±pl，并且 J（i，2j+1）=Iw（i，2j+1），即偶數列沒有發生變化，那么偶數列的像素值Iw（i，2j）=I（i，2j）.

2.2.3 復原圖像和提取水印的過程

在可逆水印算法中，水印嵌入圖片后提取水印和復原圖像的過程是一個逆向的水印嵌入過程.

對于灰度大小為M×N的已嵌入水印的圖像Iw（i，j），在接收端求出它的差分圖像函數 Dw（i，j）=M×N/2.在整個差分圖像函數中進行查詢，其中水印序列值是由下式提出的：與此同時，得到過渡復原圖像函數為Rr（i，j）：與之相對應的Rr（i，j）可以記做r（i，j）的差分圖像函數.最終要修改得到的過渡圖像函數R（i，j）就需要通過反向移動Rr（i，j）的直方圖上的點間接得到.

這個過程表現為：首先復原圖像函數的奇數列可以求出為Ir（i，2j+1）：因為在整個復原過程中圖像函數的偶數列一直沒有發生變化，所以可求得Ir（i，2j）=Rr（i，2j）.

2.2.4 實驗結果和結果分析

在仿真實驗中，我們選取的測試圖像是標準化的圖像.通過實驗數據和計算可得ph=2，pl=1，與它們相應的最大值直方值對分別為18，129和20，301，由此可以得到，圖片的嵌入容量達到了38，430位.從圖1中可以看到我們選取了大小128×128像素，(即16，384位)的二值標志圖像作為最終的待嵌入的水印圖像.

從實驗結果中可以看出，盡管在水印嵌入過程中修改了兩個最大值直方點，但最終把這些修改反射到初始載體圖像上形成的改動卻極其微小，這樣微小的改動人類視覺系統根本就無法辨別出來，但是形成的水印圖片的質量卻是非常完善的.實際情況中，由實驗數據計算得到的已形成的水印圖片的PSNR值等于46.399dB.由此可以看出，在PSNR保持比較高的情形下，應用我們提出的在差分圖像的基礎上建立的可逆水印算法，會使得圖片的嵌入容量提高很多.

〔1〕劉振華，尹萍.信息隱藏技術及其應用[M].北京：科學出版社，2010.

〔2〕王朔中，張新鵬，張開文.數字密寫和密寫分析——互聯網時代的信息戰技術[M].北京：清華大學出版社，2011.

〔3〕SalleeP.Model—Based Steganography[C]／／In Proceedings of International Workshopon Digital Watermarking.Berlin：Springer-Verlag，2004：154—167.

〔4〕Guomng Xuan，Yun Q，Shi，Jianjlong Gao，eta1.Steganal ysisbasedon Multiple Features Formedby Statistical Moments of Wavelet Character-istic Functions[C]／／Proceedings of Seventh International Workshop on Information Hiding.Springer—Verlag，2005，3727：262—277.