MATLAB模擬動力系統吸引子

馮澤夫，段秀慶，楊 航，艾文會

（華中師范大學 數學與統計學院，湖北 武漢 430079）

1 引言

MATLAB是由美國mathworks公司發布的主要面對科學計算、可視化以及交互式程序設計的高科技計算環境.它將數值分析、矩陣計算、科學數據可視化以及非線性動態系統的建模和仿真等諸多強大功能集成在一個易于使用的視窗環境中，為科學研究、工程設計以及必須進行有效數值計算的眾多科學領域提供了一種全面的解決方案，并在很大程度上擺脫了傳統非交互式程序設計語言（如C、Fortran）的編輯模式，代表了當今國際科學計算軟件的先進水平.利用MATLAB仿真模擬可以解決生產生活中很多問題，以前的蒙特卡洛方法結合計算機仿真模擬技術后不僅可以避免實驗帶來的損失可以得到非常理想的實驗結果，如燈泡的壽命的測定，戰爭的模擬……，如果真正去實驗會帶來不少的損失，而用MATLAB仿真模擬，只需要我們輸入約束條件和初始值，可以做多次試驗得到較為理想的結果.本文正是這方面應用的體現，對吸引子設計數學模型，利用MATLAB求解洛倫茲方程數值解并繪制吸引子形成的動畫，可以讓讀者真正理解吸引子形成的過程，并且在求解過程中我們發現初值不同得到的結果可能有很大變化，從而發現動力系統吸引子的混沌現象.

2 動力系統吸引子的概念及數值模擬的重要意義

動力系統在高維相空間中所描述出來的相對低維的穩定軌道被稱為吸引子.簡言之，吸引子是指這樣的一個集合，當時間趨于無窮大時，在任何一個有界集上出發的非定常流的所有軌道都趨于它.相空間中滿足以下3個條件的點的集合(可能包含1個點、有限個點或無限個點)，被稱為動力學系統的吸引子.

2.1 終極性

處于非目的態的系統“不安于現狀”，力求離之遠去，處于目的態的系統則“安于現狀”，自身不再愿意或無力改變這種狀態（也可以叫做惰性）.

2.2 穩定性

目的態是系統自身質的規定性的體現，這種規定性只有在穩定狀態中才能確立起來并得到保持，不穩定狀態不可能成為目的態；

2.3 吸引性

吸引性是目的性的根本要素，沒有吸引力的狀態不能成為系統演化所追求的目標.

吸引子是刻畫系統整體特性的概念，具有不可分割性，即不能把它劃分為兩個都滿足定義要求的 較小集合.也不能把幾個吸引子組合為一個吸引子，如平衡態A與周期態B不能合成一個單一的吸引子.吸引子分為平庸吸引子和奇異吸引子，對于平庸吸引子來說，無論初值如何，終值只有一個，而奇異吸引子卻有無數個終值，即奇異吸引子是無數個點的集合，對初值極端敏感.通過對時間序列的相空間重構，構造的奇異吸引子可在一定程度上反映出系統的演化規律，而通過分析相空間重構吸引子的結構，就可以進一步評價動力學系統的混沌特性及其變化.

而奇異吸引子可以用matlab模擬仿真它的產生，現在該方法廣泛應用于流體力學，氣象學災害預報預報，地震預測及信號處理等領域.特別的，在計算機上用洛倫茲所建立的微分方程模擬氣候變化，可以發現初始條件的極細微差別可以引起模擬結果的巨大變化—軌線的行為無法預測，這表明天氣過程以及描述它們的非線性方程是如此的不穩定，這正如眾所周知的天氣的“蝴蝶效應”即：南美洲亞馬遜河流域熱帶雨林的一只蝴蝶偶然拍動一下翅膀，幾星期后可以在美國德克薩斯州引起一場龍卷風.從而氣象學家應用此法進行天氣預報的研究.

3 模擬方案

3.1 模擬的基本思路

3.1.1 模型準備：了解問題的實際背景，明確建模目的，搜集必要的信息如現象、數據等，盡量弄清對象的主要特征，形成一個比較清晰的“問題”，由此初步確定用哪一類模型.

3.1.2 模型假設 根據對象的特征和建模的目的，抓住問題的本質，忽略次要因素作出必要的、合理的簡化假設.

3.1.3 模型構成 根據所作的假設，用數學的語言、符號描述對象的內在規律，建立包含常量、變量等的數學模型，如優化模型、微分方程模型、差分方程模型、圖的模型等.

3.1.4 模型求解 可以采用解方程、畫圖形、優化方法、數值計算、統計分析、模型對數據的靈敏性分析、對假設的強健性分析.

3.2 模擬洛倫茲吸引子

lorenz方程描述了從水桶底部加熱時，桶內液體運動的情況.加熱時，底部的液體溫度上升并產生對流現象，當提供足夠的熱量并保持不變時對流就產生不規則的運動和湍流，形成混沌系統.

3.2.1 建立模型：下面的洛倫茲微分方程組的求解過程演示了吸引子的形成過程.

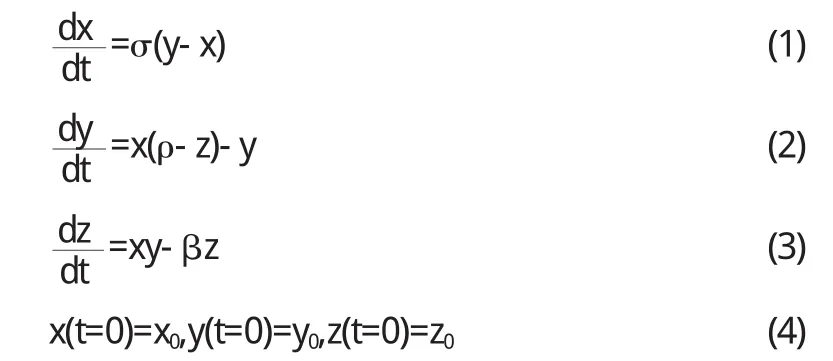
其中x正比于液體對流運動翻動的速率，y正比于液體上流與下流的溫差的變化，z正比于豎直方向的溫度梯度，式中三個參數σ（Prandtl數）、β和ρ（Rayleigh數）可任取大于0的數值，其中ρ是該動力系統中重要的參數.當系數σ、ρ、β在一定范圍內取值時，三個變量x,y,z在相空間構造的吸引子呈現出相似的結構特征.一般常用的組合是σ=10，β=，讓ρ取不同的數值，分析吸引子圖像.

3.2.2 方程的離散化:可以采用歐拉法或4階龍格-庫塔法迭代法對微分方程組求數值解.

3.2.3 洛倫茲方程求解

本文說明用Matlab工具箱求解洛倫茲方程的過程，并給出吸引子的三維動態圖象.洛倫茲方程如下：

這是一個自洽的方程組，用matlab2010求解結果如下：如圖1.

3.2.4 動態顯示吸引子并生成動畫程序略，驗證蝴蝶效應得到結果如圖2.

4 討論及結論

4.1 在ρ取不同的值時我們發現如下規律：ρ較小時如0.9，該lorenz動力系統是穩定的，吸引子最終演化到兩個奇點中的一個，而隨著ρ的值增大，系統變得越來越復雜，軌線的變化越來越難以預測，特別的當ρ取28時出現了混沌現象.

圖1

圖2

4.2 洛倫茲動力系統本身有確定的動力學方程（式（1）、（2）和（3）），該動力學方程的初值、參數值的選取直接關系到該方程是否出現混沌狀態.

4.3 吸引子之外的所有軌線最終將歸宿到吸引子范圍之內，體現出耗散系統的終態最終都將收縮到吸引子上，平庸吸引子的終值只有一個，而奇異吸引子本身由既折疊又分離的軌線構成，并且無法確定其未來的軌線的發展趨勢，這表明混沌系統是一種整體收斂而局部發散的動力學系統.

4.4 利用MATLAB語言進行計算機數值仿真模擬，求解微分方程數值解，操作簡單，圖形逼真.通過仿真實驗，讀者對混沌系統的特性和細節會有直觀深刻的理解.計算機matlab對于混沌的研究正發揮著無可替代的作用.

〔1〕姜啟源，謝金星，等.數學模型（第四版）[M].北京：高等教育出版社，2010.

〔2〕陸安山.混沌系統的仿真實現[J].欽州師范高等專科學校學報，2006（6）.

〔3〕陳永勝.基于MATLAB求解Rossler方程和模擬仿真[J].牡丹江師范學院學報，2009（1）.