基于模糊時間并具有成組約束的車間排序算法

黃錦鈿，陳慶新，毛 寧

HUANG Jin-dian1, CHEN Qing-xin2, MAO Ning2

（1.揭陽職業技術學院，揭陽 522000；2.廣東工業大學，廣州 510006）

0 引言

單元成組加工是現代制造企業應用廣泛的一種生產作業方式，該生產方式是將加工工藝相似的工件放到一組，并根據工件的工藝要求為所需要的設備分組，運用單元成組加工有利于保證工件加工質量和提高生產效率。文獻[1]認為模具型腔的加工受到EDM車間工藝條件的限制，加工型腔所用的電極必須被成組安排到同一臺設備，從而研究了后工序帶有成組特征的模具電極調度策略，并在不同的加工條件下提出相應的調度算法。文獻[2]在假定工件具有精確的加工時間和到達時間前提下，提出了一種前工序具有成組約束的兩階段柔性同序加工車間排序算法。在企業的實際生產中，往往存在大量的不確定因素，如機器故障、操作工人的熟練程度、環境參數等的影響，很少能獲得精確的加工時間和到達時間。因此，本文將在文獻[2]已有研究的基礎上，借助模糊數學理論[3,4]，將工件的加工時間和到達時間作模糊數考慮，在前工序帶成組加工約束的兩階段柔性同序加工車間中，基于遺傳算法提出一種新的啟發式算法，調度目標是為所有工件指定加工設備并確定加工順序，使所有工件經過這兩道工序的最大完成時間最短。現結合模具企業生產的實際情況，將問題進一步具體化，并提出以下假設。

假設1：各部件到達車間的時間已知但不確定，不同部件到達車間的時間不一定相同，同一部件中的工件到達車間的時間相同；

假設2：每個部件包括多個工件，且數量確定已知；

假設3：每個工件都必須經過兩道工序的加工，而且加工順序不能改變；

假設4：允許工件在工序之間等待，兩道工序之間具有無限的緩存能力；

假設5：每道工序對應的工作中心都由若干個工作小組組成，每個工作小組中有若干臺設備，各工作小組的設備數量不等且確定已知，相同工作小組中的設備工作效率相同，不同工作小組中的設備工作效率不同；

假設6：工件在各工序各工作小組需要的加工時間已知但不確定，相同部件中的工件加工要求相同，不同部件中的工件加工要求不同；

假設7：一臺設備在同一時刻只能加工一個工件；

假設8：工件一旦在設備上開始加工，不允許中途停下來，插入其他的工件；

假設9：在前工序，同一部件中的工件必須被安排在同一工作小組加工。

1 模糊時間

1.1 模糊處理

模糊數是模糊集的一種特殊形式。模糊數一般采用分段直線的方法來表示，最常用的就是三角形模糊數和梯形模糊數，其對應的隸屬度函數就是三角形和梯形。本文中工件的到達時間采用三角模糊數 來表示，其隸屬度函數公式如(1)所示：

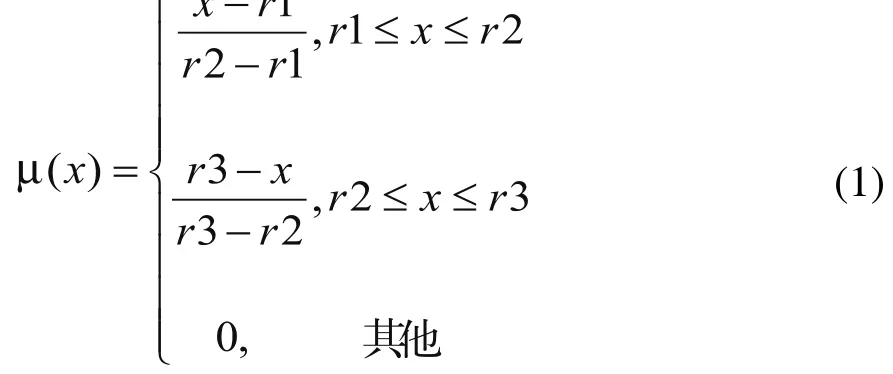
在模具企業的實際生產中，有經驗的調度員在估計某一工件的加工時間時，一般認為工件的加工時間在某一個時間區間段內都是合理的，如果低于這個時間段的下界或高于它的上界時，隨著偏離的距離越遠則其合理性就越低，即滿意度越低。因此，工件的加工時間采用梯形模糊數來表示，其隸屬度函數如式(2)所示：

在模糊調度問題中，模糊數的求和及取大操作是關鍵，求和操作用于計算工件的模糊完工時間，取大操作用于確定工件工序的開工時間。由于本文中工件的到達時間和加工時間分別采用三角模糊數和梯形模糊數，因此在求和計算工件模糊完成時間時存在兩種模糊數間的三種不同運算，根據模糊數擴張原理，模糊數的求和運算作如下三個定義。

和計算工件的完成時間一樣，在確定工件的開工時間時同樣存在三種不同的取大運算，根據模糊取大操作的原理作如下三個定義。

定義6：如果三角模糊數和梯形模糊數作取大運算，設則將三角模糊數表示為梯形模糊數的特殊形式，即三角模糊數表示為 ，因此

1.2 排序方法的選用

模糊數的比較是模糊優化的一個關鍵問題，要使得兩個模糊數之間的比較有意義必須在相同模糊度的情況下進行，雖然很多學者都在研究模糊數的比較方法，提出了各種比較指標。但是，迄今為止還沒有一個方法被公認為是最好的，所有的方法在復雜的情況下都或多或少地缺乏分辨力，甚至與人們的直覺相抵觸。實際應用中，具體采用哪種方法則主要取決于問題的本身和決策者的態度。由于本文研究的調度問題比較復雜，且在實際生產中調度人員的估計方法也是采用取均值的方式，所以本文采用均勻分布的Lee-Li法，把相關的模糊數轉化為精確值來處理。

將模糊集 的均值和標準偏差分別記為m()和σ()，借助模糊事件概率測度的概念，均勻分布的Lee-Li法用下式計算均值和標準偏差：

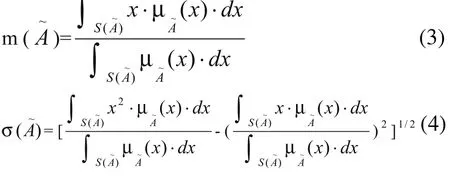
在模糊均值和模糊偏差的基礎上，Lee-Li進一步定義了模糊集綜合評判排序指標如下：

這里的β是由決策者選定的權值，它反映了均值與偏差在決策者心目中的相對重要程度,通過式(5)我們可以把模糊數轉化為精確值，以此為基礎得到目標函數值。

2 基于遺傳算法的求解過程

2.1 遺傳算法概述

遺傳算法自從1975 年由Holland 提出至今已被廣泛的應用到組合優化、機器學習、模式識別以及人工神經元網絡等方面[5,6]。遺傳算法基本流程描述如圖1所示：

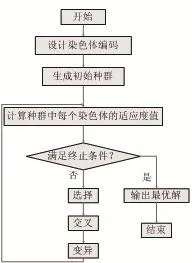
圖1 遺傳算法流程圖

2.2 編碼設計

根據本文調度問題的特點，相同部件中的工件在前工序中必須被安排到同一個加工小組加工，因此在編碼時將相同部件中的所有工件看成一個整體，同時將前工序中同一個加工小組中的機床看成一個整體。

編碼時，用自然數序列代表所有可能的部件加工順序，而不同加工小組上的部件則用‘0’隔開。對于n個部件、前階段有M個工作小組的問題，一個合法的染色體應包括n個部件符號，（M-1）個間隔符號‘0’，總長度為（n+M-1）個基因。現假設有7個部件、前工序有3個工作小組的情況，則染色體的基因編碼表示應為：[1 6 3 0 7 4 0 2 5]。則各小組上對應的部件加工順序為：M1：1→6→3；M2：7→4；M3：2→5。

從染色體的編碼信息中可以確定部件在前工序中的加工小組和加工順序，然后對比部件的到達時間和機床的空閑時間，進一步確定工件對應的機床和加工順序。這種編碼方式有利于保證滿足工件成組加工的約束，而且有利于提高搜索效率。

2.3 適應度函數設計

本文調度的目標函數值是最短的最大完成時間f(S)。按先到達先加工的原則確定工件的加工順序，所有工件通過兩道工序的最大完成時間為Cmax，現通過下面公式將目標函數值轉化為適應度函數值F(S)：

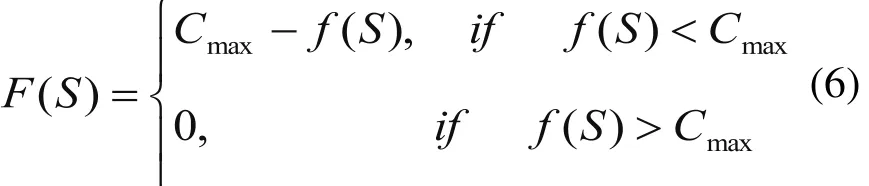
通過式（6）計算轉換，使得目標函數值較小的染色體有較高的適應度，而且各染色體將以適當的概率遺傳到下一代。

2.4 初始種群設計

為了使初始種群盡可能多樣化并且提高尋優效率，本文采用兩種方式產生初始種群。第一種方式是采用完全隨機方法產生初始種群，例如有n個待排產的部件，前工序中有M個加工小組，則首先產生由自然數1到n組成的隨機序列，然后將M-1個0隨機插入到序列中，這樣就得到一個長度為n+M-1的染色體，反復做上述操作，可以得到若干個隨機初始染色體；第二種方式是采用確定方式產生優良初始染色體，采用先到達先加工的原則可以得到一個適應度較高的初始染色體。將這兩種方式產生的染色體結合到一起作為初始種群，這樣不僅增加了種群的多樣性，而且提高了種群的進化進程。

2.5 選擇算子

選擇過程是為了從當前的群體中選出優良的個體，使他們有機會作為父代將其優良的個體信息傳遞給下一代，本文采用確定式采樣選擇方法來選擇優良的個體。具體操作步驟如下：

1）計算群體中各個個體在下一代群體中的期望生存數目Ni：

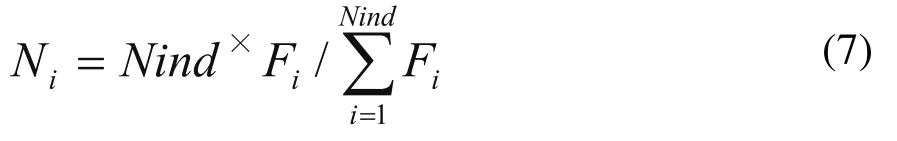
式中，Nind為種群個_體數_量，i = 1,2,3,…,Nind。

2）用Ni的整數部分確定各個對應個體在下一代群體中的生存數目。其中表示取不大于x的最大的整數。此時可確定出下一代群體中的個個體。

3）按照Ni的小數部分對個體進行降序排序，順序取前Nind-個個體加入到下一代群體中。至此可完全確定出下一代群體中的Nind個個體。

這種選擇操作方法可保證適應度較大的一些優良個體一定能夠被保留在下一代群體中，并且操作也比較簡單。

2.6 交叉算子

交叉運算是指對兩個相互配對的染色體按某種方式相互交換其部分基因，從而形成兩個新的個體，它在遺傳算法中起著關鍵作用。在交叉運算之前必須對群體中的個體進行配對，本文采用隨機配對的配對策_略，即將_群體中的Nind個個體以隨機的方式組成 對配對個體組，交叉操作是在這些配對個體組中的兩個個體之間進行的。本文每個染色體編碼包含前工序中各個加工小組的調度信息，我們將每個加工小組對應的調度稱為子調度。本文采用子調度維持交叉算子，即在兩個父代染色體作交叉運算時，在兩個父代染色體中的各取一個子調度復制到后代中，然后用另一個父代染色體剩余的編碼按順序來完成該后代的構造。交叉過程具體描述如下：

1）從一個父代染色體中找到字符“0”所在的位置，建立一個空白后代染色體，并將父代染色體中的字符“0”復制到后代染色體相應的位置；

2）從該父代染色體中隨機取出一個子調度，并將其填入所建后代染色體中的相應位置；

3）在另一個父代染色體中，將與步驟2)所取出的子調度相同的基因標記為“-1”；

4）從左到右掃描另一個父代染色體不為“0”和“-1”的基因，依次將其填入到后代染色體的其余位置。

例子：假設有2個父代Pl和P2，隨機選擇Pl和P2最右邊的子調度作為維持的子調度，交叉運算執行過程如下所示：

父代Pl：1 2 3 0 4 5 6 0 7 8 9

父代P2：2 5 8 1 0 3 4 0 6 7 9

中間執行過程：

父代Pl：1 2 3 0 4 5 -1 0 -1 8 -1

父代P2：2 5 -1 1 0 3 4 0 6 -1 -1

后代Cl：××× 0××× 0 7 8 9

后代C2：××××0×× 0 6 7 9

結果：

后代C1： 2 5 1 0 3 4 6 0 7 8 9

后代C2： 1 2 3 4 0 5 8 0 6 7 9

從上例可以看出，染色體的某一基因片段保持不變，其余基因順序將被調整，部件在前工序的加工小組分配和加工順序也將被調整。

2.7 變異算子

根據染色體編碼的特點，本文采用隨機互換兩個基因位置的變異方式，隨機交換的基因可以是工件號和工件號，也可以是工件號和“0”的不同組合，所以存在下面4種變異形式：

1）如果兩個基因都是工件，可能出現兩種情況。一種情況是兩個工件在同一加工小組上加工，這時實質是改變工件的加工順序，如下所示：

變異前：1 3 4 0 5 6 0 7 8 9

變異后：1 4 3 0 5 6 0 7 8 9

2）另一種情況是兩個工件在不同的加工小組上加工。這時變異改變染色體的工件順序和工件對加工小組的分配，如下所示：

變異前：1 2 3 4 0 5 6 0 7 8 9

變異后：1 2 7 4 0 5 6 0 3 8 9

3）如果兩個基因都是“0”，則把兩個加工小組上的加工任務對調，工件的加工順序不變，如下所示：

變異前：1 2 3 4 0 5 6 0 7 8 9

變異后：5 6 0 1 2 3 4 0 7 8 9

4）如果一個基因是“0”，另一個基因是工件，則工件的加工順序和工件對加工小組的分配都發生改變，如下所示：

變異前：1 2 3 4 0 5 6 0 7 8 9

變異后：1 2 3 4 0 5 6 7 0 8 9

3 應用實例

在某模具企業運用本文所提的方法，對14個不同時到達車間的部件進行排序，各部件包括的工件數量見表1。將各件的到達時間用三角模糊數表示，見表2。將各工件在設備上的加工時間用梯形模糊數表示，在前工序車間有大宇和威力兩個型號的數控機床，見表3和表4。

表1 各部件包括的工件數量（單位：個）

表2 各部件的到達時間（單位：小時）

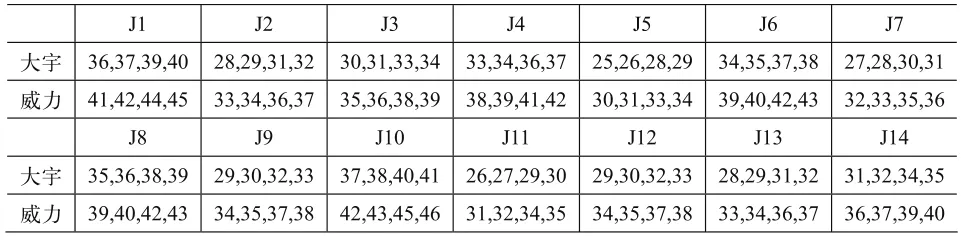
表3 各部件Ji對應的工件在前工序各設備的加工工時（單位：h）

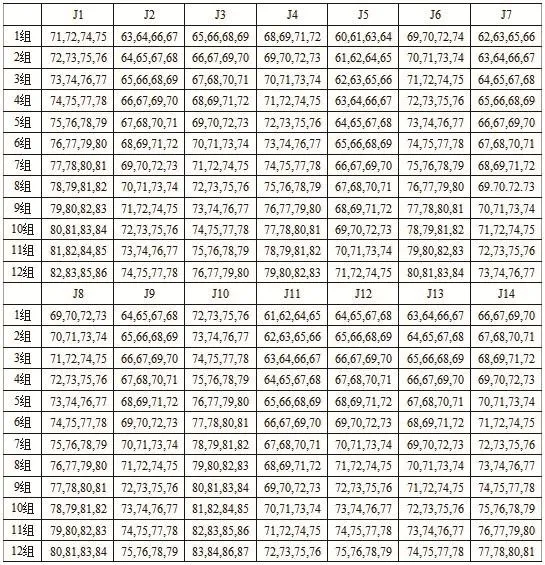
表4 各部件Ji對應的工件在后工序各設備的加工工時（單位：h）

在上述給定條件下，應用本文的遺傳算法求解，設置運行環境為初始種群染色體數為20個，交叉率為0.5，變異率為0.03，遺傳代數為12。通過eM-Plant仿真,發現最好的染色體出現在第9代，第10代，第11代，第12代。均為：[1 3 6 10 14 7 11 0 2 4 8 9 12 13 5]，各機床的計劃負荷甘特圖如下圖2所示。

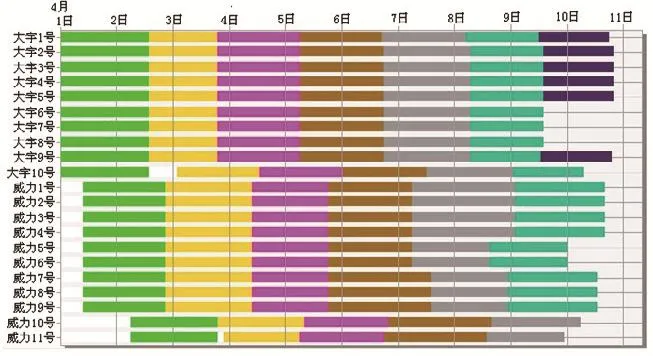
圖2 前工序各機床的甘特圖

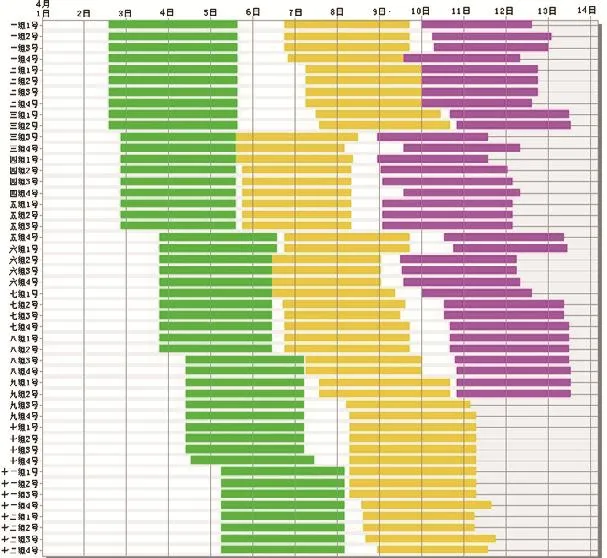
圖3 后各機床的甘特圖

運用本文提出的遺傳算法所有工件通過兩道工序的時間是325小時。如果按先到達先加工的原則確定工件的加工順序，通過兩道工序的最大完成時間是369小時，單純按照Johnson法則確定工件的加工順序，最大完成時間將是415小時。從這些運行結果對比可以看出，該遺傳算法的排序結果優于其它算法，而且計算時間為半秒，適合應用于車間現場。

4 結束語

本文研究了前階段帶有成組約束的兩階段柔性同序加工車間的排序問題，考慮了具有模糊加工時間和模糊到達時間的情況，分別用梯形模糊數和三角模糊數來表示加工時間和到達時間，采用均勻分布的Lee-Li法將模糊數轉化為精確值，通過遺傳算法優化排序，應用企業的實際算例仿真說明該算法的有效性和可行性。

[1] 孫吳勝.考慮后工序帶有成組特征的模具電極調度策略的研究[D].廣州:廣東工業大學.2007.

[2] 黃錦鈿,陳慶新,毛寧.具有成組約束的柔性同序加工車間的排序算法[J].工業工程,2011,V14(2):112-117.

[3] Slowinski R,Hapke M.Scheduling under fuzziness[M].New York:Physica-Verlag.2000.

[4] J.Peng,B.Liu,Parallel machine scheduling models with fuzzy processing times[J],Information Sciences,166,49-66,2004.

[5] 盧永超,陳慶新,毛寧.基于遺傳禁忌搜索算法的模具電火花車間調度[J].工業工程,2008,11(5):80-85.

[6] 盧永超,陳慶新,毛寧.模具電火花加工車間的非同等并聯機混合遺傳算法[J].計算機集成制造系統,2009,15(3):587-543.