數學建模教學優秀教學案例解析
——交巡警服務平臺的設置與調度
木 仁,白阿拉坦高娃,崔 巍
(1.內蒙古工業大學理學院 數學系,內蒙古 呼和浩特 010051;2.內蒙古大學 數學科學學院,內蒙古 呼和浩特 010021;3.赤峰學院 數學與統計學院,內蒙古 赤峰 024200)
數學建模教學優秀教學案例解析
——交巡警服務平臺的設置與調度
木 仁1,2,白阿拉坦高娃3,崔 巍1
(1.內蒙古工業大學理學院 數學系,內蒙古 呼和浩特 010051;2.內蒙古大學 數學科學學院,內蒙古 呼和浩特 010021;3.赤峰學院 數學與統計學院,內蒙古 赤峰 024200)
隨著全球經濟社會的快速發展,數學建模已經成為了眾多學科領域中的焦點問題.各種數學建模方法的推廣依然成為了數學建模教學的必要環節.一個優秀的數學建模案例不僅能夠真實的反映現實問題同時也能多方面體現數學建模方法.交巡警服務平臺的設置與調度問題是一種較為理想的數學建模案例.它不僅能夠從多方面體現數學建模方法、培養學生們的創新意識,同時也可以推廣到眾多實際問題中應用.
Matlab;最短路;線性規劃;0-1整數規劃;非線性規劃;層次分析方法;擬合
1 引言
隨著計算機軟件功能的拓展,眾多復雜的數學建模方法均得到了很好的解決[1].同時也有部分典型案例已經在實踐當中得到廣泛的應有.然而,由于眾多非數學專業學生及非重點院校學生們的數學建模知識的欠缺及計算機應用能力的短板,大部分數學建模方法均未得到很好的推廣.在解決實際問題時數學模型的建立及求解同等重要,只懂得其中的一個往往不能很好的解決實際問題.過去的眾多數學研究工作者雖然具備了扎實的數學建模理論基礎,但由于計算機編程能力的缺乏不能求解出復雜的數學建模問題,而新一代的數學研究工作者雖然具備了一定的編程技巧,但由于數學建模理論知識的欠缺往往不能很好的建立相關模型.這為眾多數學建模教學工作者提出了新的挑戰.今后,應該怎樣推廣數學建模教育,提高不同專業學生的創新意識,特別是非數學類專業學生及非重點院校學生們的數學建模能力及求解能力變的尤為重要[2-3].
數學建模所涉領域眾多,它不僅能夠培養學生們的創新能力,同時也能夠為不同學科領域創造出的經濟社會價值[4].數學建模方法多樣,需要掌握的知識點較多[5].怎樣通過數學建模的課程將眾多數學建模方法傳授給學生們是數學建模教育工作者的所追求的目標[6].對于眾多重點院校的學生來說許多數學建模方法都能夠較快的接受.然而,對于非數學類專業學生或非重點院校學生而言數學建模方法的傳授卻是十分困難.特別是隨著大范圍的擴招,使得非重點院校根本就不能夠招收具有扎實數學基礎的學生.對于這些學生,應進一步探索傳授數學建模方法的方案.其中最為可行的方法就是選擇恰當的數學建模案例對不同的數學建模方法進行全方面的解析.這使得數學建模案例的選取變的十分重要.頻繁的引進不同案例必然會導致大部分學生在短時間內難以接受相關問題.如果能夠通過少數幾個案例將眾多數學建模方法傳授給學生那是最為理想的.
2011年全國大學生數學建模競賽題目交巡警服務平臺的設置與調度題目是一個較為理想的數學建模教學案例.所涉及到的數學建模方法包括Matlab作圖,Matlab編程,最短路問題,行遍性問題,計算機模擬,線性規劃,非線性規劃,層次分析方法,數據的統計分析,數據擬合,綜合評價等眾多方法.以下對其進行深入的分析討論.
2 問題的提出
由于警務資源是有限的,如何根據城市的實際情況與需求合理地設置交巡警服務平臺、分配各平臺的管轄范圍、調度警務資源是警務部門面臨的一個實際課題.
試就某市設置交巡警服務平臺的相關情況,建立數學模型分析研究下面的問題:
(1)附件1中的附圖1給出了該市中心城區A的交通網絡和現有的20個交巡警服務平臺的設置情況示意圖,相關的數據信息見附件2.請為各交巡警服務平臺分配管轄范圍,使其在所管轄的范圍內出現突發事件時,盡量能在3分鐘內有交巡警(警車的時速為60km/h)到達事發地.
對于重大突發事件,需要調度全區20個交巡警服務平臺的警力資源,對進出該區的13條交通要道實現快速全封鎖.實際中一個平臺的警力最多封鎖一個路口,請給出該區交巡警服務平臺警力合理的調度方案.
根據現有交巡警服務平臺的工作量不均衡和有些地方出警時間過長的實際情況,擬在該區內再增加2至5個平臺,請確定需要增加平臺的具體個數和位置.
(2)針對全市(主城六區 A,B,C,D,E,F)的具體情況,按照設置交巡警服務平臺的原則和任務,分析研究該市現有交巡警服務平臺設置方案(參見附件)的合理性.如果有明顯不合理,請給出解決方案.
如果該市地點P(第32個節點)處發生了重大刑事案件,在案發3分鐘后接到報警,犯罪嫌疑人已駕車逃跑.為了快速搜捕嫌疑犯,請給出調度全市交巡警服務平臺警力資源的最佳圍堵方案.(具體圖及附件參見網站http://www.mcm.edu.cn中的2011年競賽題目)
3 數學建模教學內容解析
在上一節中提出的問題所涉及數學建模方法較多.本節中將對其進行詳細的分析,并指出每一問中可傳授的數學建模方法.
數學建模方法傳授點之(一)Matlab在數學建模中的應用
Matlab軟件因其豐富的工具箱,目前已經成為了數學建模領域最為得心應手的軟件[7].同時,由于Matlab在處理數據時與Excel文檔,TXT文檔及數據庫文檔等之間的特殊接口,使得數學建模者可以隨心所欲的讀寫和處理各項數據.在處理數據的同時也可將部分內容可視化的顯示出來,這使得研究工作者對數據有了更為深層次的認識.在數學建模時不僅需要將眾多數據規范化,更需要數據結果的可視化,而在這方面Matlab軟件能夠較為簡便的實現具體的目標.
3.1 數據的可視化顯示方法
在題目中給出了各個節點的相關信息. 其中通過各節點的坐標,與該點連接的節點標號及節點是否為交巡警服務平臺等信息,可將各區的分布圖顯示出來.此時,主要通過Matlab中的簡單循環語句及作圖方法即可畫出圖形.其中繪制出的A區圖形如圖1所示.在A區中已有20個交巡警服務平臺,圖1中的圓圈就是20個交巡警服務平臺.整個城區圖形及其圍堵方案示意圖如圖2所示.圖2中帶有箭頭的線段指出了圍堵交巡警服務平臺及出口.
3.2 數據的讀寫及處理方法
在進行作圖時需要將已有數據讀到Matlab工作區中使用.具體讀取方法有以下三種:
A 直接將Excel數據拷到Matlab中的m文件中,并賦給某一變量;
B 通過Excel的加載宏工具建立Matlab數據與Excel數據之間的相互讀取功能;
C 通過Matlab中的xlsread函數將Excel中指定文件讀至Matlab工作區.
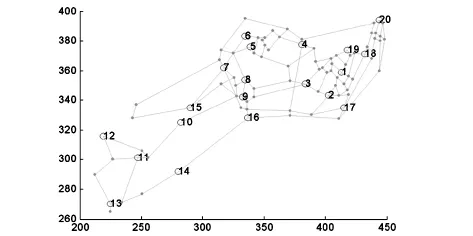
圖1 A區的交通網絡與平臺設置的示意圖
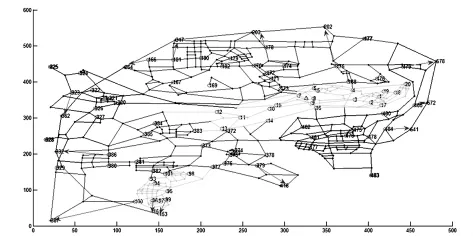
圖2 城區的交通網絡與平臺設置的示意圖
3.3 Matlab函數的編寫與結果的存儲
在計算節點與節點之間的最短路時首先需要計算連接節點之間的距離.通過,Matlab中已經讀入的數據及距離函數可計算獲得連接節點之間的距離.由于在求解最短路時需要使用該結果,故需保存該數據.具體存儲方案有:
A 直接將數據保存為全局變量以便隨時進行調用;
B 通過Matlab與Excel之間的接口將其放置到Excel中;
C 通過Matlab中的xlswrite函數將數據寫入的Excel中.(低版本的Matlab軟件沒有寫入功能,需要使用Matlab7.0及以上版本)
3.4 利用工具箱求解數學模型
在Matlab工具箱中包含了眾多數學建模現成軟件.其中常用且較容易使學生們學會的數學建模軟件主要有:
A 線性規劃Matlab求解函數linprog:線性規劃理論[8]在數學領域基本趨向于完備化的階段.然而,線性規劃在實踐當中的應用仍然沒有得到普及.主要原因在于懂得線性規劃的研究工作者基本都是科研工作者.很少有研究工作者將其投入到實踐當中應用.而相反需要用到線性規劃的人并不知道線性規劃能夠為其帶來的經濟社會價值或根本不可能學會線性規劃模型更不用說線性規劃模型的求解了.
隨著經濟社會的發展,落后或發展中國家必然將會從勞動密集型轉化為技術進步型.而技術的進步離不開數學建模眾多方法.其中較易普及的便是線性規劃.毫不夸張的說現如今能夠通過軟件能夠解決復雜決策問題或不同類型決策問題的人過于缺乏,其中包括眾多教師.那么這一理論及實踐的推廣就可想而知了.從而今后的數學教育特別是非重點院校應該更加重視學生們的理論與實踐的結合及簡單理論的深層次推廣.而不是漫無目的的傳授多種復雜的理論.但部分教師特別是學基礎數學出身的教師過于迷醉與自己所學領域的探索,而并未考慮到在當今時代本可以盛行的優秀數學理論及其求解方法的推廣.這也在部分程度上體現了作為大學數學老師所缺乏的各學科全面發展的能力.
B 整數規劃Matlab求解函數:在實踐當中整數規劃的使用率也不比線性規劃差多少.其中對于大部分決策問題0-1規劃可能更具實用性.本文中提出的題目即是一個典型的例子.這一例子還可以進一步推廣到管理中心的選擇問題等眾多問題.
在Matlab中0-1整數規劃的求解函數為bintprog.對于普通類型的整數規劃可通過線性規劃函數的四舍五入的方法獲取.對于不滿足約束條件的特殊情況可進一步對變量進行約束的方法獲取較優的可行解.
lingo軟件當中可直接通過變量的整數約束獲取整數規劃問題的最優解.但lingo軟件的數據讀取及處理功能遠不及Matlab軟件.
C 非線性規劃的Matlab求解:在Matlab中提供了無約束優化問題的求解算法.而由于非線性規劃問題可通過引進輔助函數將其轉化為無約束最優化問題.
D 微分方程的Matlab求解:在Matlab中不僅可以對微分方程進行數值計算,同時也提供了微分方程的符號計算方法.
E 數據的統計描述、分析及模擬方法.
F 回歸、插值與擬合.
數學建模方法傳授點之(二)最短路問題及行遍性問題
為了給各個交巡警服務平臺分配管轄范圍,需要計算各個節點之間的最短距離.由于已經得知了與每個節點連接的節點標號及連接節點之間的距離,故根據Dijkstra算法可獲得某一頂點至各個節點的最短距離的同時也可通過Floyd算法獲得每個節點之間的最短距離.算法的具體思想及方法參見參考文獻[5].
交巡警不僅需要對管轄范圍內的案件進行快速的處理,同時為了避免案件的發生也需要對管轄范圍內進行定期的巡邏,而這一問題正是數學建模方法中的行遍性問題.
目前隨著網購熱潮的興起,大部分快遞公司急需懂得快件的投放及管理的人才.在這一過程中管理者必需懂得最短路問題及行遍性問題方能更加全面快捷的投遞快件.因此將部分數學專業學生培養為該方面的人才是一個較好的出路.
數學建模方法傳授點之(三)線性規劃問題
在不考慮交巡警服務平臺的工作量的前提下,各個交巡警服務平臺分配管轄范圍的確定問題歸結為每個節點與服務平臺之間的距離的最小化問題.在得知各個節點之間的最短距離的前提下只需通過Matlab循環語句就可以通過逐個比對分配管轄方法.
除了上述分配管轄范圍的方法之外,還可以0-1建立線性規劃模型對其進行求解.由于為各個交巡警服務平臺分配管轄范圍,使其在所管轄的范圍內出現突發事件時,盡量能在三分鐘內有交巡警到達事發地,這一問題等價于為各個交巡警服務平臺分配管轄范圍,使得從交巡警服務平臺到各個節點的距離總合最短的問題.從而,可建立如下0-1整數規劃模型:
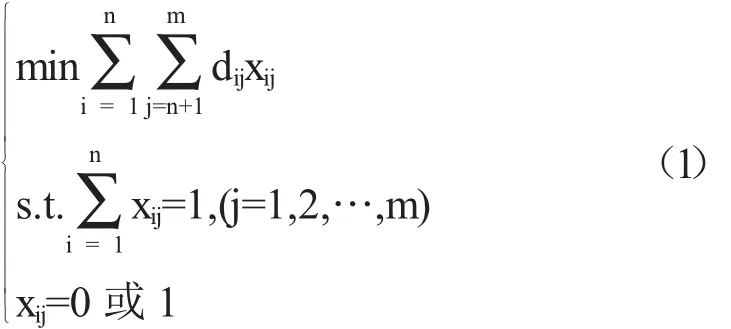
上式中xij表示第j個節點是否屬于第i個交巡警服務平臺的管轄范圍,如果屬于則xij=1,否則xij=0.約束條件表示第j個節點必須屬于某一交巡警平臺管轄范圍.dij表示第i個節點到第j個節點的最短距離.
對于重大突發事件,需要調度全區20個交巡警服務平臺的警力資源,對進出該區的13條交通要道實現快速全封鎖.實際中一個平臺的警力最多封鎖一個路口,請給出該區交巡警服務平臺警力合理的調度方案.該問題轉化為在20個交巡警服務平臺中選出13個交巡警服務平臺,使得該13個服務平臺到13條交通要道之間的距離總合最短.從而針對這一問題建立如下0-1規劃模型
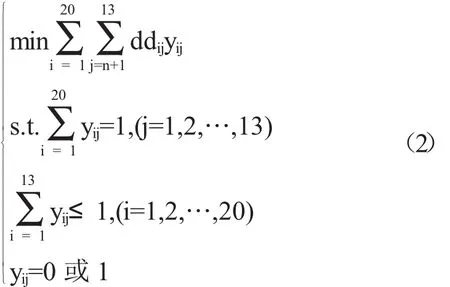
上式中ddij表示城區A中第i個交巡警服務平臺到第j條交通要道的出口節點之間最短距離.約束條件表示第j個出口必須由某一交巡警服務平臺所封鎖;表示第i個交巡警服務平臺至多封鎖一個出口.
同理如果該市地點P(第32個節點)處發生了重大刑事案件,在案發3分鐘后接到報警,犯罪嫌疑人已駕車逃跑.為了快速搜捕嫌疑犯,需給出調度全市交巡警服務平臺警力資源的最佳圍堵方案.該問題等價于80個交巡警服務平臺對17個出口的圍堵問題,為了盡快進行圍堵,需要讓圍堵時所行使的路線長度總和最小化,從而可建立出如下0-1規劃模型:

上式中dddij表示第i個交巡警服務平臺至第j個出口的最短距離,ddddj表示第32節點至第j個出口的最短距離.約束條件dddijzij+3000≤ddddj表示第i個交巡警服務平臺如果封鎖第j個出口,則第i個交巡警服務平臺到第j個出口之間的距離再加上3分鐘的行駛時間3000m后的距離要小于等于案發現場到第j個出口的距離.其它約束條件的解釋與(2)式類似.
上述三個0-1整數規劃模型并不復雜. 但由于數據量較大,很難通過人工輸入系數矩陣.因此,必需借助計算機工具計算出各個最短距離,然后通過算法生成各個系數矩陣.其中存在著大量的稀疏矩陣,通過循環語句可以較快生成.
如果利用Lingo等線性規劃軟件進行求解,不僅在數據的讀寫方面存在較多問題,且隨著變量個數的提高短時間內難以計算獲得最終結果.
數學建模方法傳授點之(四)非線性規劃問題通過模型(1)分配出來的各個交巡警服務平臺的工作量并不均衡,每個交巡警服務平臺的總發案率為
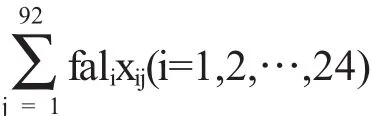
為使各個交巡警服務平臺的工作量均衡,需要調整各個交巡警服務平臺所管轄的節點或節點個數,使得每一個服務平臺的案發率盡量接近發案率平均值,即與發案率平均值之間的差距總和最小化,同時必須滿足與交巡警服務平臺之間的距離小于3000m(即3分鐘內能夠到達案發現場),從而建立如下模型:
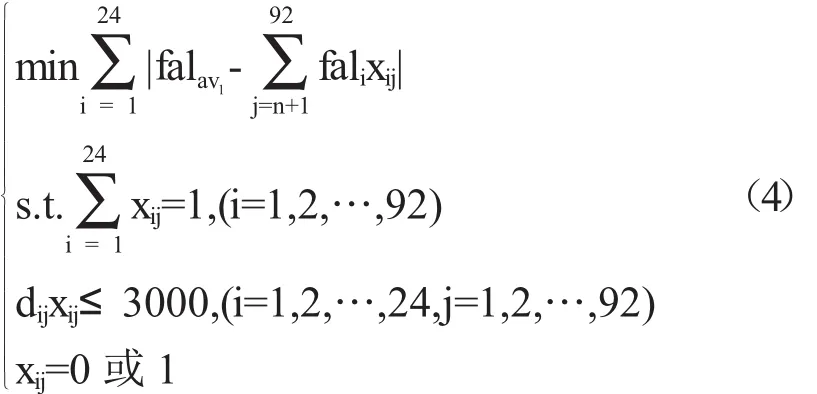
該模型等價于
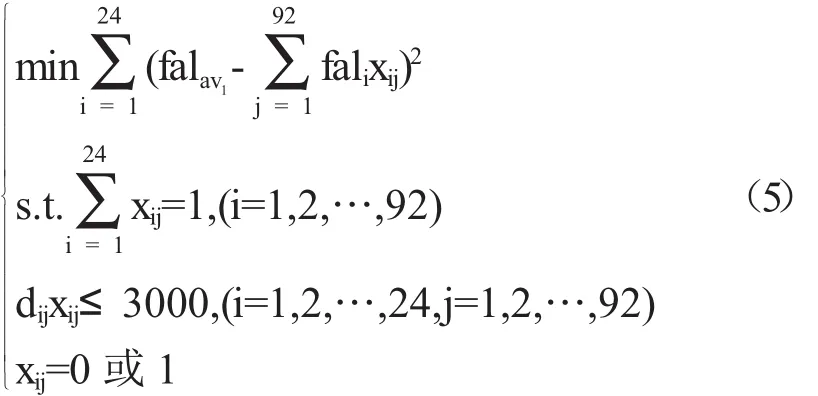
上述模型為二次規劃模型,通過Matlab中的quadprog函數加以求解,但quadprog函數只能求解一般情形下的二次規劃,不能求解決策變量為0-1的二次規劃.因此模型(4)和模型(5)還需要尋求相關非線性規劃理論求解方法[9].
數學建模方法傳授點之(五)數學模型的可行求解方法
由于模型(5)是一個0-1二次規劃模型,因此當變量的個數相對較少時完全可以通過窮舉法及神經網絡方法加以求解.
由于通過最短距離容易得知與交巡警服務平臺距離小于3000m的所有節點.從而模型(5)可利用人工分配的方法加以求解.但該方法只能近似獲得最優解.
在求解模型(5)時可獲得每個節點的最優分配方案(將節點分配給距離最近的交巡警服務平臺).但這必然會讓部分交巡警服務平臺的工作量過高或過低.此時,可設定每個交巡警服務平臺工作量的上線,然后逐一將各個節點分配出去.在分配過程中可根據最優分配方案及次優分配方案的差距分配各個節點.
數學建模方法傳授點之(六)層次分析方法
在評價交巡警服務平臺設置的合理性時,決策者需要考慮眾多因素.不同因素在不同程度上影響著交巡警服務平臺設置的合理性.同時每一個因素又受到相應子因素的影響.在確定各個指標權重時需要利用層次分析方法來確定.
利用Matlab不僅可以較簡單的計算出各個特征值及特征向量,同時還可以用較簡單的算法確定各個指標的權重.相對其它眾多軟件Matlab是一個較好的層次分析方法權重確定軟件.
數學建模方法傳授點之(七)擬合
在確定交巡警服務平臺平均應承擔的報警次數時需要考慮城區面積、城區人口及單位面積人口數量之間的關系.城區面積相對穩定,但城區面積將隨著城市的經濟社會發生改變.從而需要通過以往數據計算擬合[10]出交巡警服務平臺平均應承擔的報警次數與城區面積、城區人口及單位面積人口數量之間的關系.
4 結論
全國大學生數學建模競賽已經成功舉辦了20年.在這二十年期間數學建模雖然得到了一定的推廣,但數學建模的教學工作有待提高.特別是對非重點院校及非數學專業學生數學建模的教學工作更需加強.數學建模的教學工作的提高應優先從教師做起.只有教師的數學建模能力提高的一定水平才能夠推動數學建模教育.而一個優秀的數學建模實例,必將為教師及學生們的數學建模能力的提高起到至關重要的作用.交巡警服務平臺的設置問題是一個較好的數學建模實例.且該題目可以進一步推廣到廠址的選擇問題,管理中心的確定問題等眾多熱點問題中.
〔1〕姜啟源.數學模型[M].北京:高等教育出版社,1997.
〔2〕葉其孝.數學建模教學活動與大學生教育改革[J].數學實踐與認識,1997,27(1):92~94.
〔3〕王茂芝,郭科,徐文皙,周游.數學建模中的創新意識培養[J].大學數學,2009,25(1):126~129.
〔4〕李尚志.培養學生創新素質的探索——從數學建模到數學實驗[J].大學數學,2003,19(1):46~50.
〔5〕趙靜,但琦.數學建模與數學實驗[M].北京:高等教育出版社,2008.
〔6〕李炳照,王宏州,孫華飛,陳一宏.數學建模思想融入數學類課程的思考與實踐[J].高等理科教育,2006(5).
〔7〕羅建軍,楊琦.Matlab 教程[M].北京:電子工業出版社,2006.
〔8〕何堅勇.運籌學基礎[M].北京:清華大學出版社,2008.
〔9〕袁亞湘,孫文瑜.最優化理論與方法[M].北京:科學出版社,2006.
〔10〕盛驟,謝式千,潘承毅.概率論與數理統計[M].北京:高等教育出版社,2008.
O29
A
1673-260X(2012)05-0017-05
內蒙古自治區自然科學基金項目(批準號:2011MS1002);內蒙古大學“211工程”創新人才培養項目資助

