基于GOMS的圖書館界面定量分析及效率測量

袁新芳

(河南城建學院圖書館，河南 平頂山 467036)

1 引言

計算機和通訊設備已廣泛應用到圖書館的信息服務中，但這些設備從根本來講是為圖書館用戶服務的。圖書館應樹立以人為本的服務理念，使用戶在應用這些信息設備和信息技術時注意力不會分散，并感覺到方便、舒適。用戶在享受信息服務的過程中接觸最多是圖書館門戶網站的用戶界面，用戶界面一般是由電子窗口和鼠標控制的菜單構成。如果我們在設計和改進界面時對界面進行定量分析并對界面的信息效率進行定量評價，同時既能考慮到用戶的需求也能考慮用戶的弱點，就能使圖書館的界面更加人性化，更加受到用戶的歡迎［1］［2］。

2 圖書館界面的定量分析

可以用許多定量的方法來分析圖書館網站的界面，筆者利用GOMS模型目的(goals)、對象(objects)、方法(methods)和選擇規則(selection rules)來分析。該模型能夠預測在圖書館網站界面下，用戶或工作人員執行一次信息行為操作所需的時間。［3］［4］

當我們面對兩個不同的圖書館界面時，細微的速度差別能影響到用戶的信息心理、決策需求、對圖書館的評價。我們通過GOMS模型對網站界面進行分析、修正網站界面的設計，使用戶快速地獲得高度精確的信息。

2.1 GOMS擊鍵模型分析

用戶在實施某一信息行為過程中，所花費的時間是各種基本操作所需時間的總和。雖然不同的用戶可能花費的時間不同，但研究者發現無論是使用鍵盤操作還是用圖形輸入設備來完成信息行為，在比較分析中只需要使用一組典型的時間，而不需要測量每個具體個體的時間。經過細致的實驗，給出了各個基本操作的一組代表時間(見表1)。在這里，每個時間用一個字母來代表。

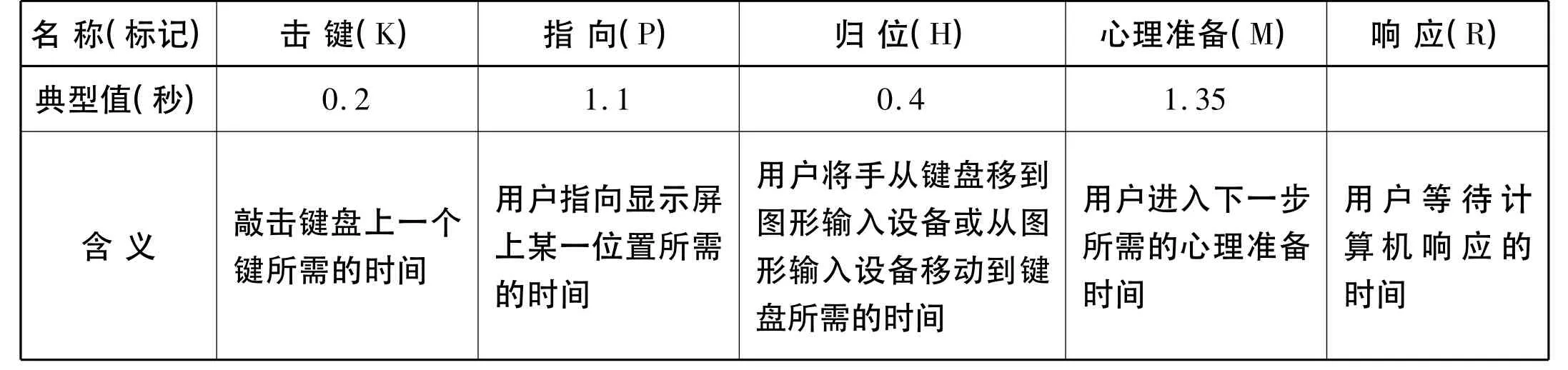
表1 基本操作時間表

在實際的操作過程中，不同的人打字的速度是不盡相同的，那么他們擊鍵所花費的時間(K)也不可能相同。不同的用戶具有不同的性格、脾氣，那么他們的指向(P)、歸位(H)、心理準備(M)等操作上所花費的時間也不同。即便是同一用戶在實施信息行為的過程中的不同心情、精神狀態、信息需求狀態，也會影響用戶在指向(P)、歸位(H)、心理準備(M)等操作上所花的時間。圖書館不同的計算機設備有不同的配置，那么它們對用戶信息需求的響應時間也是不同的。用戶信息檢索提問式的不同表達，計算機設備對用戶信息需求的響應時間也是不同的。由于每個度量值的可變性，我們不能用這個簡單模型來確定絕對時間值，但是可以通過使用典型值，來比較和評判兩種或兩種以上圖書館界面設計的優劣。從而來改進我們的設計方案。

2.2 GOMS模型分析中用戶定位心理規則

我們在圖書館的界面上，完成信息行為時，需要完成一系列的基本操作(K、H和P)，它們是建立GOMS模型的一部分。建模難點在于判斷用戶在何時會停下來進行無意識的心理活動，也就是心理準備時間M。下面列出用戶定位心理活動的基本規則。

規則1 M的初始插入：在K(擊鍵)之前插入M。在用于選擇命令的P之前插入M。但是對用于選擇命令參數的P，不要插入M。

規則2 預期M的刪除：如果M前面的操作符能完全預期M后面的一個操作符，則將該M刪除。

規則3 同一認知單元內M的刪除：如果一串MK屬于同一個認識單元，則除了第一個以外的所有M。

規則4 連續終結符之前M的刪除：如果K是一個認識單元后面的多余分隔符，則將之前的M刪除。

規則5 作為命令終結符的M刪除：如果K是一個分隔符，且后面緊跟一個常量分符串，則將之前的M刪除。

規則6 重疊M的刪除：如果M與計算機響應的時間(R)重疊，則需刪除M。

2.3 GOMS模型的實證分析

假定圖書館用戶欲將中圖法分類號與主題詞相互轉化，必須使用鍵盤或者圖形輸入設備(GID)來輸入給出分類號，不存在語音或者其他輸入方式。在設計界面時，我們理想的目標是這種轉換的時間最小化，速度和精確度最大化，屏幕資源不受限制。同時這種操作的窗口或者顯示區域已經被激活，并且等待著用戶從鍵盤或者GID輸入。當轉換結果顯示在屏幕上時，用戶的任務已經完成了。再假定用戶在使用界面時，每次輸入的分類號平均需要5個字符，包括小數點和符號。同時用戶的輸入是完美的，沒有錯誤。那么分別對對話框界面和圖形用戶界面進行GOMS模型實證分析。

2.3.1 對話框界面分析

用戶操作過程如下：

·把手移動到對話框：H

·指向需要的單選按鈕：HP

·點擊單選按鈕：HPK

·將手重新移回到鍵盤：HPKH

·輸入五個字符：HPKHKKKKK

·敲擊回車：HPKHKKKKKK

根據規則1，我們在所有的K之前插入M。P之前插入M。

HMPMKMHMKMKMKMKMKMK

根據規則2，刪除可以預期的M(PMK變成PK)和字符串之間的M。

HMPKHMKKKKKMK

我們將這些操作所花費的時間累加起來。

假若用戶進行第二次操作，各種選項已被選中，那么操作過程如下：

那么用戶每次操作的平均時間為(7.35+3.9)/2=5.6 秒。

2.3.2 圖形用戶界面分析

界面運用刻度尺的圖像來指示分類號，另外一個刻度尺的圖像來指示主題詞，用戶可以通過拖動GID上下移動的箭頭指示分類號的刻度尺，另外一個刻度尺的箭頭會自動指向相應的主題詞。在整個操作過程中，用戶不需要輸入任何字符，只是在刻度尺上選擇分類號。根據需要，用戶可以伸長或收縮刻度尺，也可以改變量程。當用戶改變分類號的刻度尺時，另外一個刻度尺會自動調整，顯示出相應的主題詞。用戶根據自己的需要可展開或收縮刻度尺，直接把箭頭指向下位類或上位類。為了迅速地定位遠處的分類號，用戶不僅可以展開或收縮刻度尺，還可以向上或向下翻卷，直到期望的分類類號在觀察范圍內，然后將箭頭移動到期望的分類類號附近，直到達到期望的精確度。

下面我們分析使用該界面的最短時間

·用戶將手移動到GID，在需要的箭頭處按下GID按鈕并保持不放：HPK

·用戶移動箭頭，直到箭頭指向正確的數值，然后松開GID按鈕：HPKPK

·根據規則1插入M：HMPMKMPMK

·根據規則2刪除三個M：HMPKPK

通過累加各個操作的時間，用戶使用的總時間為：

這種計算模型適用一種幸運的狀態，就是用戶期待的分類號在預先設定的合適量程內，刻度尺并處于合適的分辨率范圍內。如果用戶要伸長刻度尺才能看到期待的分類號，通過更改量程，收縮刻度尺才能達到合適的分辨率，然后移動箭頭。用戶需要用箭頭翻卷若干次，每次翻卷動作都需要若干次操作。然而計算機顯示翻卷的動畫，也需要一定時間。假定我們用S表示翻卷時間，S大約為3秒鐘。那么用戶的操作程式如下：

HPKSKPKSKPKSKPKK

根據規則1那么可以得到

HMPKSKMPKSKMPKSKMPKK

在實際操作過程中，分類號刻度尺初始時就設定在合適位置的情況很少。用戶使用該界面完成一次信息行為需要16秒左右的時間。

通過GOMS模型對以上兩個界面進行了實證分析，那么哪個界面更好、更適合用戶的需求，結果就出來了。

3 圖書館界面效率測量

GOMS模型分析可以計算用戶使用圖書館網站界面完成一項信息行為需要多長時間;但它不能告訴我們可以期待的界面運行的效率有多高。我們可以用信息學的方法，來研究圖書館界面效率的測量。

用戶為了表達自己的檢索需求，需要在圖書館網站界面上輸入一定量信息。為了測量圖書館網站界面的效率，我們可以確定用戶某項信息檢索任務需要提供信息量的最小量值，這個量值與界面的設計沒有關系。假設某一圖書館網站界面所采用的方法需要輸入的信息量比最小量值多，那么用戶可能做了一部分無用功，該界面的效率就不高，需要改進和提高。如果圖書館網站的界面需要用戶輸入的信息檢索需求的信息量正好等于最小量值，那么這界面的效率最高。

網站界面的信息效率(E)是指為完成某項任務所需最小信息量除以用戶實際需要提供的信息量。信息效率的最大值為1，最小值為0。

當用戶被要求提供完全不需要的信息時，信息效率(E)可以為0，在實際工作中，有許多圖書館界面的效率居然為0。譬如界面上的對話框只允許用戶有一個選擇(如OK按鈕)。

網頁界面的信息效率(E)只涉及完成任務系統所需的信息量和用戶提供的信息量。不同網頁界面的信息效率(E)相同，但是總的花費時間卻不同。一般情況下，信息效率(E)高的界面它的反應速度更快、更人性化。但在實際工作過程中也會出現界面的反應速度與界面信息效率成反比的情況，不過這種情況較少。

信息量一般是用比特(Bit)來計算，一個比特就是一個信息單位。它的含義是在兩個選項中作出選擇。譬如，開與關、是與否、0與1。如果我們在4個事物中做出選擇，就需要2比特的信息。假定事物是a、b、c和d，第一個比特選擇ab或cd，如果我們選擇了ab，那么第二個比特可以選擇a或b，兩次二分的選擇，也就是說2比特，就足夠從4個事物中選擇出一個。從8個事物選擇，需要3個比特;從16個事物中選擇需要4比特;依此類推。如果我們給出n個可能的選項，它們傳遞的信息總量是

Log2n

它們中任意一個的信息量是

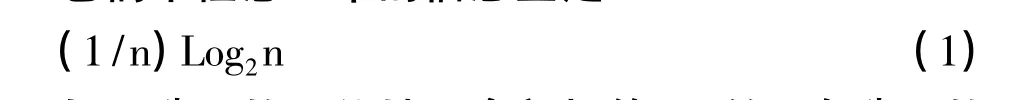
如果選項的可能性不全部相等，且第i個選項的概率是P(i)，那么第i個選項的信息量是：

總的信息量是表達式(2)(對于所有選項)的總和。在等概率下，就轉化為表達式(1)。對于只允許點擊一個按鈕的界面來說，信息的含量是0比特，不點擊按鈕是不允許的。

假設我們點擊界面上唯一的按鈕可以破壞一個物體，那么是不是點擊就傳達了信息了嗎?不是的，原因是不按此按鈕不是可以選的選項。界面“只允許點擊唯一的按鈕”。但是假定按鈕在3分鐘內不被點擊，就錯過了允許毀壞的物體的時間，那么并不是點擊就會傳遞1比特。因此在這種情況下有兩種可能的信息。從表達式(2)中，我們可以計算涉及物體被破壞的概率P，那么它不被破壞的概率是1-P。根據表達式(2)，可以計算這個界面的信息含量

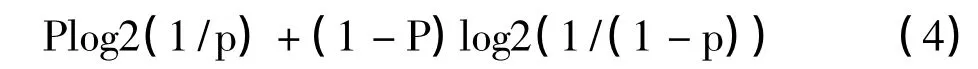
當P=1/2時，對表達式(4)求值如下：

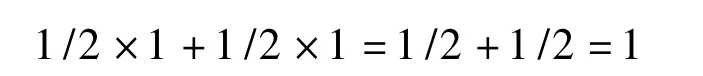
若P≠1/2時，表達式(4)值就小于1

若P=0或P=1時，表達式(4)值就為0。正如表達式(3)所示。

也就是說，我們只有了解可能收到的消息的上下文環境，才能測量一條消息的信息含量。特別強調的是，為了計算收到消息的信息量，我們必須知道發出該消息的概率。一條消息的信息量與其他的任何消息無關，與發生時刻和持續時間無關，與其他任何事件無關。

但是，用戶在實施信息行為時，可以用馬爾可夫過程更精確地建模，即后面的信息行為的概率依賴于用戶前面的行為。我們在此探討的前提是用戶的信息行為是獨立的和等概率的。［6］

我們也可以計算非鍵盤設備傳遞的信息量。假定顯示器被分為兩個域，一個標有“yes”，另一個標有“no”，在其中一個區域內的一次點擊就提供了1比特的信息。如果有n個具有同等可能性的目標，通過一次點擊可以提供Log2n比特的信息。假如目標的大小不同，每次點擊的信息量不變，但是將鼠標移到較小的目標要花費更多的時間。我們就會計算出花費時間的多少。即便是目標的出現概率不同，計算公式與已經給出的非等概率鍵盤輸入的情況也相同。

4 結語

以上我們利用GOMS模型對圖書館網站的界面進行了定量分析，并利用GOMS模型分別對對話框界面、圖形用戶界面進行了實證研究，為設計、修改、改善圖書館網站的界面提供了參考依據。利用信息論的方法結合GOMS模型對圖書館界面效率測量進行研究，可以指導和評價圖書館網站界面的設計質量。

［1］李賀，沈旺，國佳.國外數字圖書館評價研究現狀分析［J］.中國圖書館學報，2010(06)：88-94.

［2］許江濤.網絡信息資源的評價與利用［J］.圖書館工作與研究，2010(10)：69-72.

［3］李炯，汪文勇，繆靜.GOMS模型在考試登分系統中的應用研究［J］.計算機科學，2005(4)：219-224.

［4］Card，Stuart K.Thomas P.moran and Allen Newell.The Psyohology of Human-ComputerInteraction［M］.Hillsdale，NJ：Lawrence Erlbaum Associates，1993.

［5］Gray，Wayne D.Bonnie E.John and Michael E.Atwood.Project Ernestine：Validating a GOMS Andlysis for Predicting and Explaining Real-world Task Performance［J］.Human-Computer Interaetion，8：3 PP.

［6］Shannon，Claude E and Warren Weaver.The Mathematical Theory of Communication［M］Urbana：University of Illinois Press 1998.