基于模糊隨機理論的顎式破碎機齒板結構設計
閆海燕
(安徽開發礦業有限公司 六安 237462)
0 引言
目前破碎機械制造業在我國的總體規模已相當龐大,但是其發展和競爭力仍然不足,基礎零部件主要還是進口,使其發展受到很大的制約。所以現今我們應該加大對破碎機基礎技術和部件的研究,增強自主研發能力。
我國破碎機制造業有著非常廣泛的市場前景,將應用到建筑、水利、化工、煤礦、冶金等眾多行業。其中最重要是水泥行業、鋪路和礦山領域的應用,其破碎機的使用占整個行業的約30%。
1 顎式破碎機齒板結構
齒板是破碎機中的重要零件,結構簡單,但影響到破碎機的生產率、比能耗和破碎力等。顎式破碎機在破碎物料時齒板會直接和物料接觸,會受到研磨和擠壓,承受的沖擊力非常大,就會產生嚴重的磨損,是破碎機主要的易損元件之一。因此延長齒板的壽命成為大家重視的問題。
傳統的齒板設計方法是在齒板的某一點集中施力,再除以齒板的受力面積,就獲得齒板受力,再研究和設計齒板的結構參數,采用這種方法忽略了齒板的載荷是不均勻分布。分析報廢的齒板看出,齒板的磨損橫斷面上,中部的磨損最嚴重,兩端磨損最少;縱斷面上,磨損在進料口方向少,出料口方向多。同時齒板破碎力的合力點位置是變化的,因此其受力隨機,我們需要仔細分析齒板的受力情況,在此基礎上改進齒板的結構參數,改善顎式破碎機齒板的使用壽命。本文采用的模糊隨機理論更是為這一研究提供了理論基礎。
2 模糊隨機理論分析
模糊隨機理論結合了模糊性和隨機性,它包含模糊數學、隨機數學、概率論、統計學等多門學科。模糊隨機理論可以求解不確定性問題和工程數據問題。模糊可靠性分析法需要準備充分的數據確定結構參數的隸屬度函數。在實際情況下,并不容易得到不確定量的準確數據,需要采用如經驗法、實驗法等多種方法得到數據。
出現了模糊數的區間期望值視為隨機集合和區間平均值,稱為可能性分布。本文介紹可能性平均值、變量和協方差等的表示,研究了加權模糊數區間可能性和區間隨機平均值的關系。研究表明,用隨機理論可以計算模糊數線性組合的加權變量,同樣可以用來確定隸屬度函數值。
設基本事件是一個離散事件,基本空間表示成:
對應于基本事件的概率:

如果模糊隨機事件A的隸屬函數可測,其中某一元素xi屬于的隸屬度為mf(xi),隸屬度函數的期望值就是模糊隨機事件的概率。
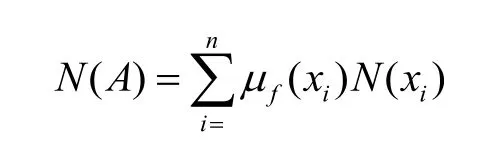
只要確定模糊隨機事件的概率、隸屬度函數和基本事件的任何兩個,就能求解出第三個。本文根據經驗和齒面的磨損情況來求出模糊隨機事件的概率N(A)和隸屬度mf(xi)。先對齒板進行模糊隨機載荷法,然后再對齒板進行有限元分析、模型修改和有限元再分析。
3 齒板的受力分析
3.1 計算齒板破碎力概率分布
根據齒板的最大破碎力的作用點,把齒板分為上下部分研究,每個齒板有m個齒,將總破碎力分成上下破碎力分布概率N(B1)和N(B2)來計算。破碎力概率事件表示為:
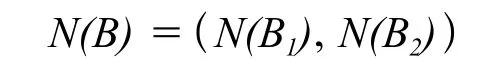
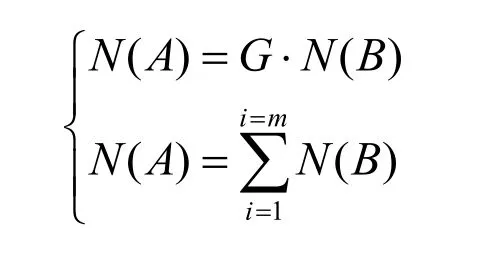
上式中,G表示破碎力的權重函數。
N(A)歸一化處理后得到N(Ai)通用表達式,即齒板破碎力的概率分布函數:
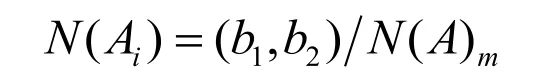
本文中假設N(BI)=1,破碎力作用點位置N(A)=0.6 ,歸一化處理得到顎式破碎機的破碎力概率分布函數是:
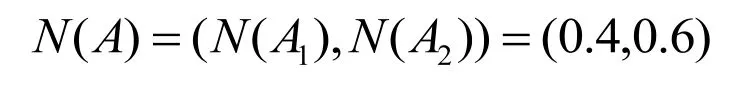
3.2 計算各齒面的破碎力
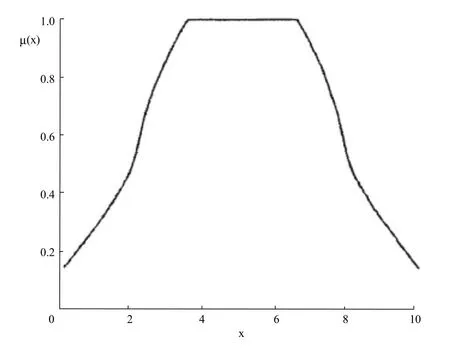
圖1 齒板橫向隸屬度函數
本文的PE250×400顎式破碎機在獲取了齒板破碎力的概率分布后,進一步計算齒板的破碎力大小:
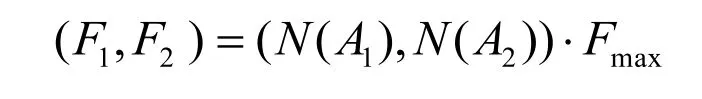
根據實際情況,下齒板受到的破碎力最大,在有限元分析中,只計算下齒板來簡化隸屬度函數 m(x)的計算:mx= (ax1,ax2,!,axm)。
齒板的隸屬度函數一般如圖1所示。
對齒板的隸屬度函數求和 :
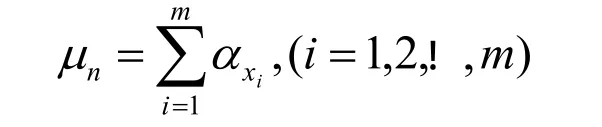
歸一化處理求和公式后,獲得齒板齒面歸一化隸屬度函數,還用mx表示:
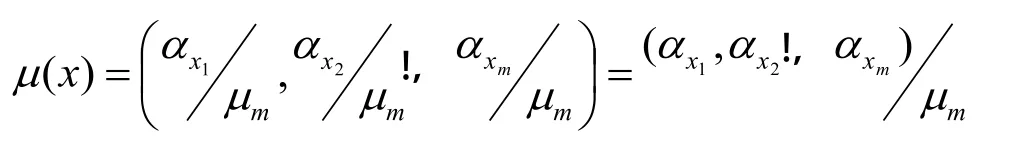
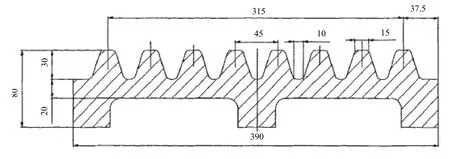
圖2 PE250×400動顎齒板截面示意圖
解出齒板各齒面的破碎力F(x): F' (x) = F2·mX。如圖2所示為PE250×400動顎齒板截面圖,該齒板有8個齒,取隸屬度函數之和mm(x) = 4.6,歸一化計算m (x)得:

取齒板的100mm長度進行研究,采用有限元分析齒板受力和變形,受力計算得:

4 有限元改進齒板參數結構
PE250×400顎式破碎機的齒板材料采用ZGMnl3-2,彈性模量為2.0×105MPa,泊松比為0.29,密度為7850kg/m3,屈服應力最大33lMPa。
圖3為PE250×400動顎齒板的有限元應力分析結果。由圖3所示,齒板的最大應力為125MPa,最小是0.26MPa。圖4為齒板的有限元位移分析結果,其最大位移為3.37×10-5m,這是個相當小的尺寸,因此忽略位移情況進行分析,只研究齒板結構參數對應力在齒板分布的影響。按照材料的屈服應力和有限元分析出最大應力,計算出安全系數為2.47。齒板的應力集中在齒板的中間部位,我們各增加1個凸臺,這樣它就和其它三個凸臺尺寸一樣,再用有限元進行分析。齒板的最大應力變為37.4MPa,最小應力是0.05 MPa,明顯改善了應力大小和集中,安全系數也提高到8.85。但在新加的齒板上又出現了應力集中,需要在最中間加寬為80mm,再進行有限元分析。將中間凸臺加寬后最大應力的改變不大,說明我們進行的改進比較合理。
再改變齒板凸臺高度來進行有限元分析,分析結果看出修改后,齒板的最大和最小應力變化不大,這表明凸臺高度的變化對齒板受力影響很小,可以適當縮短齒板凸臺高度結構。
可見改進齒板結構參數十分合理:改進后齒板的應力分布很大改善,但是材料基本沒有增加;另外齒板安全系數明顯提高,這樣就能延長齒板的使用壽命,降低破碎機破碎成本。
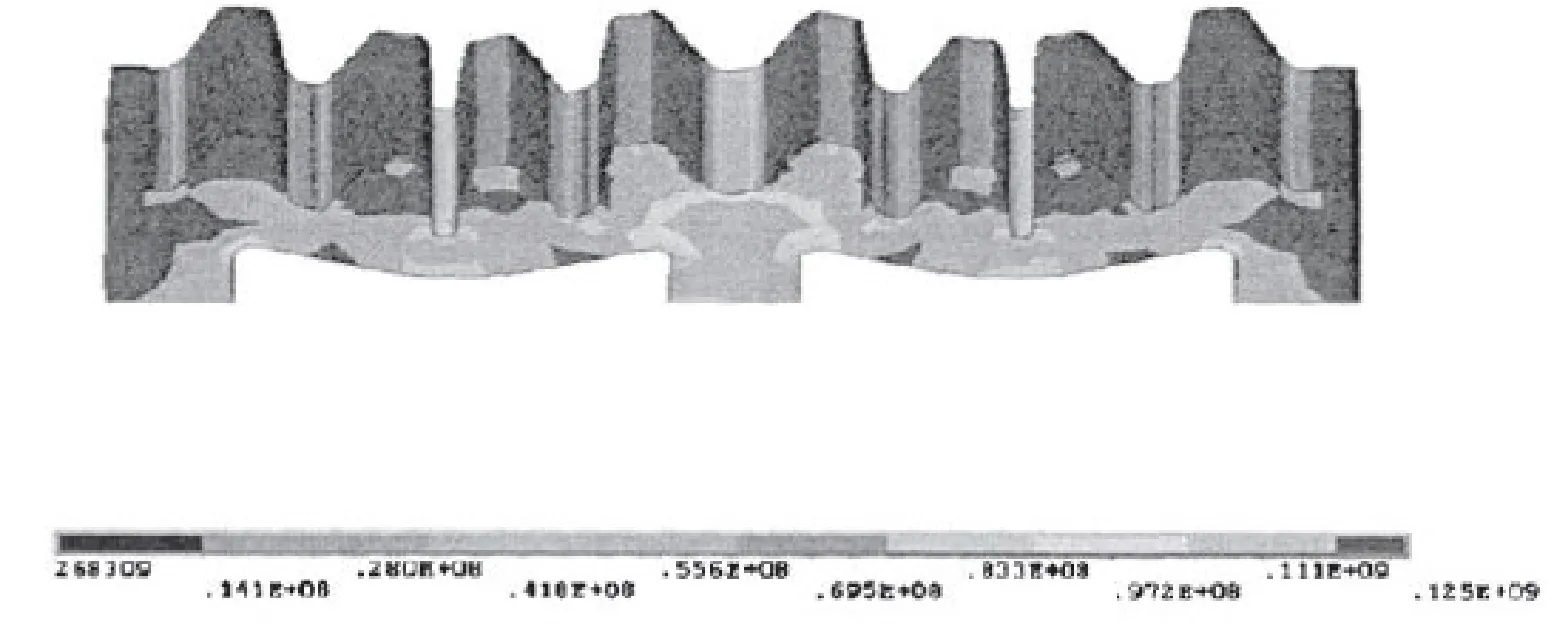
圖3 PE250×400動顎齒板應力分析結果
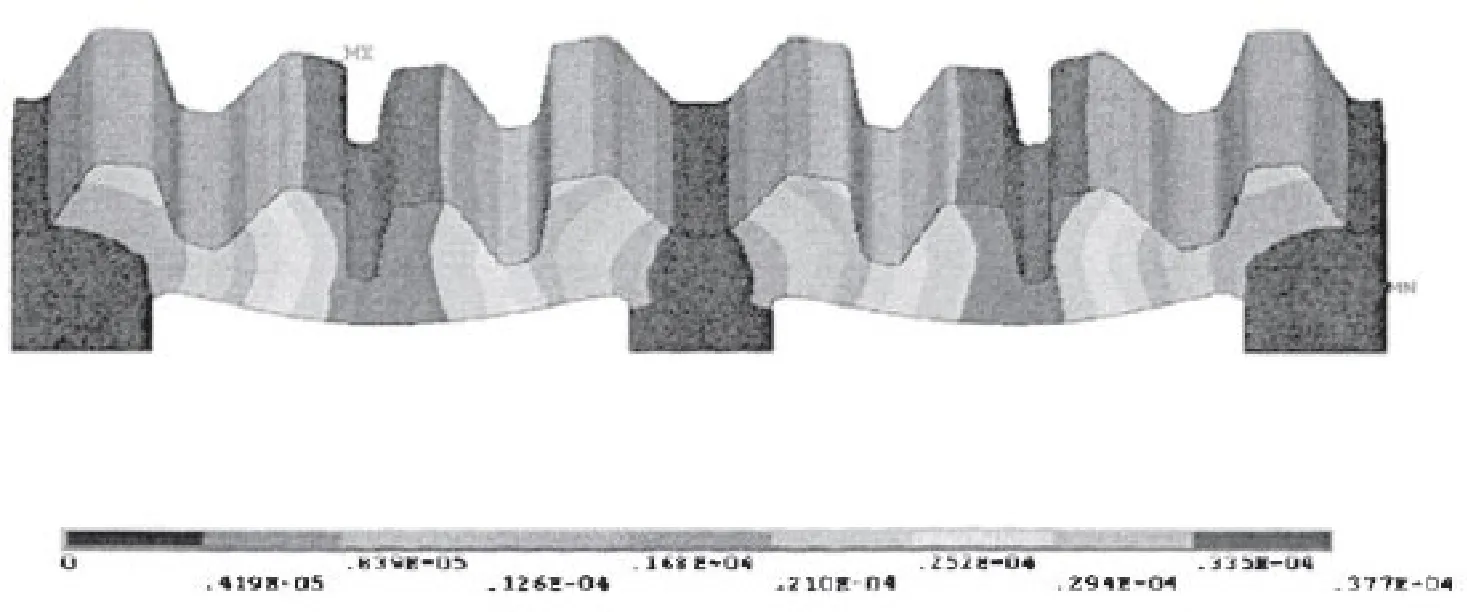
圖4 PE250×400動顎齒板位移分析結果
5 改進齒板結構參數
在實際中設計齒板時,為了方便,通常從齒板高度的中間位置分成兩部分。我們為動顎齒板進行如下修改:
將一塊齒板修改為兩塊相同的組合齒板;凸臺高度從30mm變為15mm;厚度從20mm變成15mm;在保持齒頂和齒底間距以及齒根不變,將其高度從30mm改為35mm,齒頂寬從15mm改為12mm;修改后的兩塊齒板重量之和減少了18.26kg,這樣節約了生產和使用成本;有限元分析結果表明,修改后齒板的應力分布改善很大,應力分布也比較均勻。
6 結束語
本文針對PE250×400顎式破碎機的齒板在物料加工過程中受損嚴重,壽命較短的情況展開研究,采用模糊隨機理論加載齒板受力狀態,并計算了齒板的應力分布,進行了有限元分析。通過改變齒板結構參數,改進齒板應力分布,保證在節約材料的前提下降低了能耗,延長齒板的使用壽命,提供了可靠的理論基礎。
[1]傅彩明, 饒綺麟.模糊隨機理論在齒板類零件有限元仿真中的應用研究[J].湖南科技大學學報, 2006, 21(1): 33-351.
[2]張勝民.基于有限元軟件ANSYS7.0的結構分析[M].北京: 清華大學出版社, 2003.
[3]Germanovich, L.N,Dyskin, A.V Fracture mechanisms and instability of openings in compression, 2000, 37(1):334-340.
[4]廖漢元, 孔建益, 鈕國輝.顎式破碎機[M].北京: 機械工業出版社,2008,1-50 .
[5]孫成林.破碎機械回顧與展望[J].有色礦冶, 2005, (21):134-137.

