基坑放坡開挖破壞性狀大變形有限元分析
火映霞,侯新宇
(1.江蘇城市職業學院 城市科學系,南京 2100172.江蘇城市職業學院 建筑工程系,南京 210017)
0 引言
近年來,隨著我國經濟和科技發展水平的提高,大量巖土工程開始建設,人們對于邊坡穩定和破壞性狀的分析也越來越多。而與傳統的極限平衡分析方法比起來,有限元法已經逐漸成為分析該問題的有效方法之一。對此,國外一些專 家, 如 Naylor,Griffi ths & Lane以 及 Potts &Zdravkovic等人都進行過類似的研究,并提出了多種有限元法的分析技巧,對于其優點的列舉也比較明確。值得一提的是,Naylor,Griffi ths&Lane二人提出了一種理想彈塑性模型——Mohr-Coulomb 模型,該模型對于邊坡等的破壞性狀進行了分析,他們認為,在對巖土工程進行有限元的分析中,非常重要的一點就是選擇土體本構的模型,而這又受土質類型的制約[1]。因此,其在研究中表示,通常情況下,軟塑性土無法頻繁的軟化成為非常明顯的形態,所以,在對這類材料進行分析的過程中,可以采用簡單的彈塑性本構模型;而在微超固結與正常固結土中,因為其可以承受固定的塑性應變,則可以采用塑性性狀的軟化模型來對其破壞性狀進行分析,實踐也證明,采用這種方法也比較符合實際。而Potts &Zdravkovic則在Mohr-Coulomb 模型以及修正劍橋模型的基礎上,對多種情形下的邊坡開挖性狀進行了分析[2]。我國也有一部分專家對邊坡穩定和破壞性狀進行過深入的研究,并給出了很多建設性的結論。
本文在Mohr-Coulomb模型的基礎上,通過采用理想彈塑性本構模型和考慮應變軟化的本構模型(不考慮軟化),對平面應變下的軟土均質地基上的基坑放坡開挖進行大變形有限元計算,同時也對比了非軟化和軟化模型的結果,從而重點探討了基坑放坡開挖時的破壞性狀。
1 軟化模型在有限元計算當中的選擇
Mohr-Coulomb在表述材料時,認為軟粘土可以分別采用非軟化(理想彈塑性)模型和軟化模型來進行表示。由此,我們可以將結構性軟粘土的應力和應變之間的關系曲線用圖1來表示。
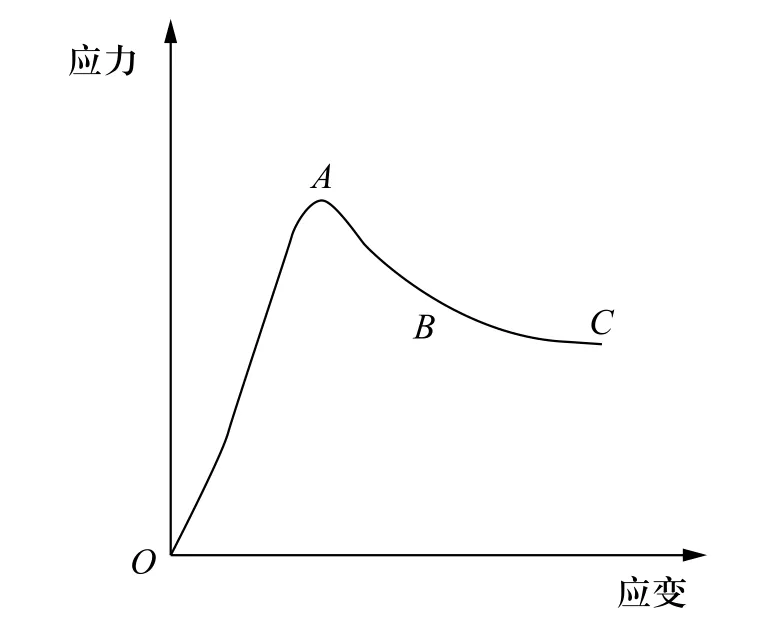
圖1 結構性粘土典型應力應變曲線
由圖1可知,該曲線可以分為三個部分。OA段:當峰值應力大于應力的時候,當應力逐漸變大時,土體也會隨之逐漸屈服,從而使土體硬化,這種情況下,其應力和應變的關系可以描述為非線性彈性關系,或者也可以成為彈塑性關系;AB段中,當應力達到峰值后,土體的強度會下降,應變和應力會成反比關系,此時,軟粘土會呈現應變軟化的現象;BC段中,當土體與殘余應力值接近的時候,基本上會呈現為完全塑性的狀態。
為了對土體的軟化現象進行準確和簡單的描述,其應力和應變的關系可以通過分段線性函數來進行模擬,而軟粘土結構性破壞造成的應變軟化現象則可以采用線性軟化來進行描述。一般情況下,以上關系基本上有以下兩種表達方式,一為簡單線性軟化模型[3],如圖2所示;二為復雜線性軟化模型[4],如圖3所示。
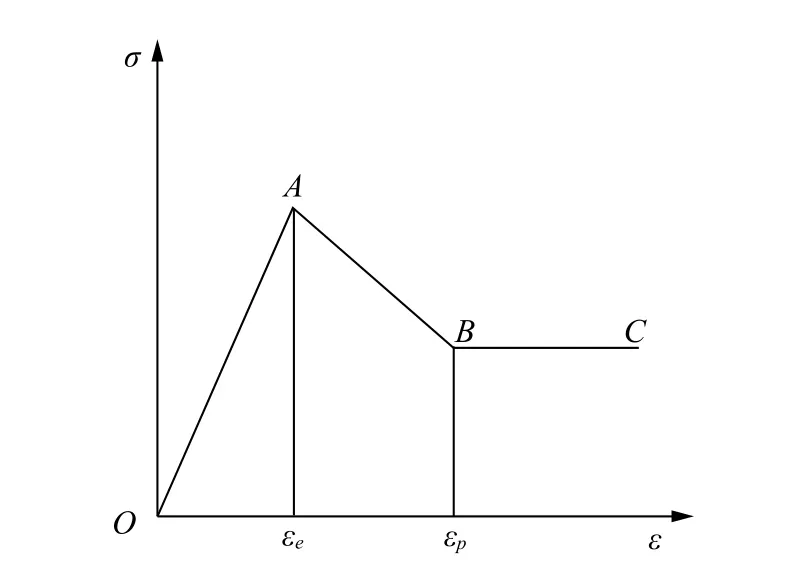
圖2 簡單線性應變軟化模型
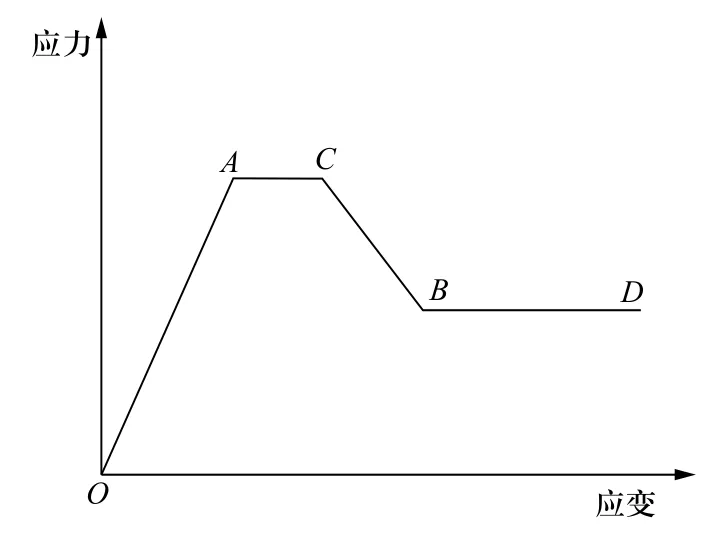
圖3 復雜線性應變軟化模型
圖2、圖3中,A、B兩點分別對應初始屈服面以及最終屈服面,當應力達到A點,即應力峰值時,如果繼續加荷的話,土體就會開始軟化,此時,應變會隨著應力的下降而逐漸發展。但是,當應力在B點以后時,材料會開始無限流動,此時材料被破壞。
因此,為了更好地模擬基坑開挖土體的破壞性狀,應該采用應變軟化模型。本文采用Mohr-Coulomb模型,以求和圖2能夠對應起來,此時,軟粘土的抗剪強度參數選擇如圖4所示。
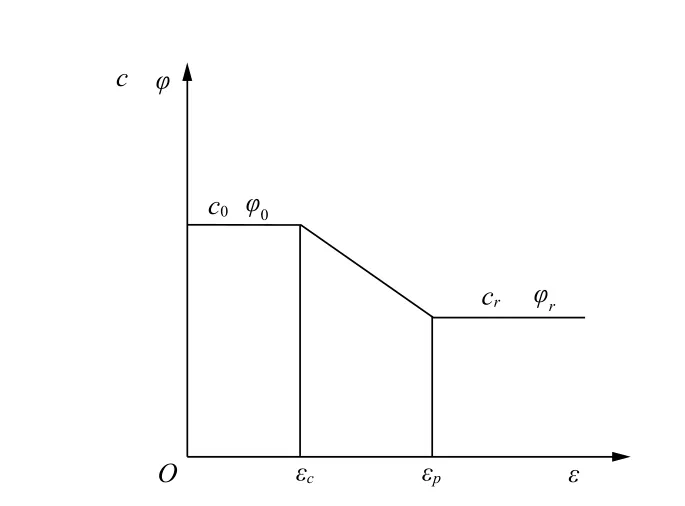
圖4 簡單線性應變軟化模型參數選擇
由圖4可以看出,在只有彈性應變卻沒有塑性應變的情況下,將c0、φ0設為Mohr-Coulomb軟化模型中的強度參數,此時,當塑性應變在εe時,強度參數不變,仍然為c0、φ0;當塑性應變在εp和ε時,強度參數為cr、φr;當塑性應變在εe和εp時,強度參數為c0、φ0、cr、和φr的線性差值。
2 均質軟土地基放坡開挖非軟化的分析
大多數對于基坑放坡開挖破壞性狀大變形的研究工作中,都采用Eulerian和Lagrangian的描述方法,其中,前者主要為流體力學,后者為固體力學。通常而言,以上兩種辦法分別有著明顯的優勢,但不可否認的是,其也存在著一定的缺陷。因此,為了彌補以上兩種方法的缺點,可以采用任意拉格朗日–歐拉(ALE)進行描述。在這種方法中,計算網格能夠在空間內按照任意形式進行運動,也就是說,其可以在空間坐標系與物質坐標系內獨立運動。與此同時,其可以按照合適的、規定的網格運動方式來對物體的移動進行準確的描述。由此可知,在ALE的描述當中,參考構形為已知條件,而現時構形與初始構形都為未知條件,需要對其進行求解。因此,ALE描述方法現在被廣泛的應用在求解大變形的問題上。
本文針對不排水條件下軟粘土的快速開挖進行分析,過程當中采用總應力法。因此,在非線性理想彈塑性土體模型中Mohr-Coulomb 準則在有限元分析過程中需要用到粘聚力、剪脹角、內摩擦角、泊松比以及楊氏模量等參數,表1為分析過程中涉及到的土體材料參數。

表1 土體材料參數
另外,在本次分析當中,坡度比為1:2,圖5所示為開挖過程。
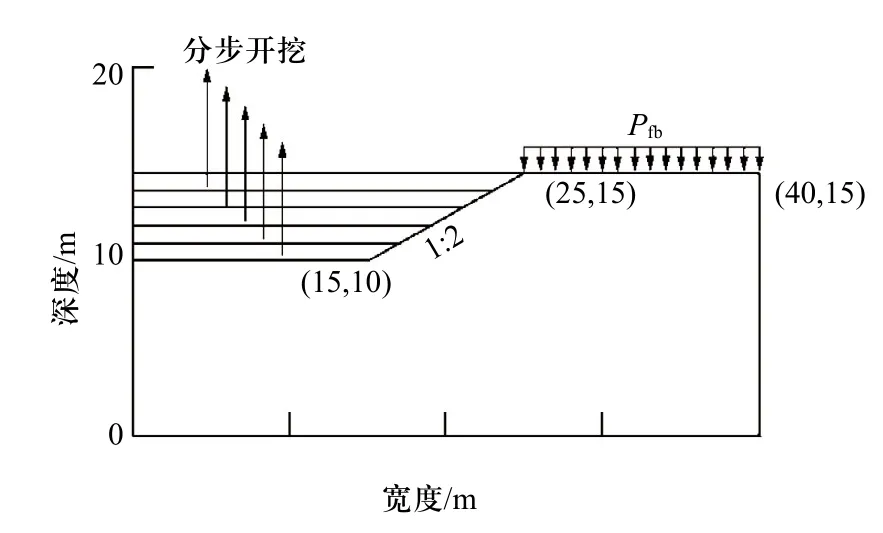
圖 5 基坑放坡開挖過程示意圖
在圖5中,我們假設開挖時的地表荷載fbP恒為 15kPa,且各次開挖的深度均為1米,直到開挖基坑被破壞。此時,有限元分析當中,共劃分出2400個網格,2501個節點。
我們知道,基坑放坡開挖實際上是土體荷載向側面進行卸載的一個過程,具體說來,就是土體向側面卸載的變化和大小,會導致土體中的應力重新進行分布,從而使得土體的性狀產生變化,最終使其應變發生變化[5]。
在基坑放坡開挖的過程當中,軟粘土剪切帶的變化規律如果用塑性剪應變來表示的話,可以分為如下四個階段:1)當開挖深度到達2m的時候,在軟粘土的局部地區會產生剪切帶,但范圍相對較小;2)當開挖深度到達3m時,剪切帶會隨著土體向側面卸載的應力增加而增大,其范圍也會相應逐漸增大;3)當開挖深度到達4m的時候,剪切帶范圍會持續擴展;4)當開挖深度達到一定范圍時,如5m,則剪切帶會持續發展,并最終貫通,這時,基坑的土體剪切帶會發生滑移的現象,即基坑會失去穩定性,并最終被破壞。
3 均質軟土地基放坡開挖的軟化分析
與之前非軟化分析有所區別的是,本次前2次開挖的深度均為1m,其后每次都按照0.5m的深度進行開挖,直到基坑失去穩定性,發生破壞。
我們知道,在對基坑放坡開挖進行軟化分析的過程,其實和非軟化分析的區別不大,其也是土體荷載向側面進行卸載的一個過程。因此,仍然采用塑性剪應變表示的剪切帶的發展來分析基坑放坡開挖破壞的情況。分析結果如下:1)當開挖深度達到2 m的時候,在軟粘土的局部地區會產生剪切帶,但范圍相對較小;2)當開挖深度到達2.5m和3m時,剪切帶會隨著土體向側面卸載的應力增加而增大,其范圍也會相應逐漸增大;3)當開挖深度到達3.5m的時候,剪切帶會持續發展,并最終貫通,這時,基坑的土體剪切帶會發生滑移的現象,即基坑會失去穩定性,并最終被破壞。
由以上分析可知,在基坑放坡開挖的過程當中,和非軟化分析的結果比起來,軟化分析的結果有著相對比較明顯的區別。也就是說,當基坑開挖進行到一定深度以后,在軟化分析的過程當中,基坑頂部和基坑底部比起來,會更早發展成為塑性狀態;而在非軟化分析的過程中,則會變成基坑底部比基坑頂部更早達到塑性狀態。
4 結束語
綜上所述,應變軟化條件下的分析結果和非軟化條件下的分析結果有著相對而言比較明顯的不同。即當基坑開挖進行到一定的深度之后,在軟化分析的過程當中,基坑頂部和基坑底部比起來,會更早發展成為塑性狀態;而在非軟化分析的過程中,則會變成基坑底部比基坑頂部更早達到塑性狀態。除此之外,如果從圖形化分析的角度來說,在非軟化分析當中,其剪切帶有著比較明顯的貫通過程,但在軟化分析的過程中,則比較復雜,因此,可以認為,非軟化分析的結果相對不安全。
[1]GRIFFITHS D V, LANE P A.Slope stability analysis by fi nite element[J].Geotechnique, 1999, 49(3): 387-403.
[2]DAVID M Potts, LIDIJA Zdravkovic.Finite element analysisin geotechnical engineering: application[M].London:Thomas Telford, 2001.
[3]蔣明鏡, 沈珠江.考慮剪脹的線性軟化柱形孔擴張問題[J].巖石力學與工程學報, 1997, 16(6): 550-557.
[4]沈珠江.理論土力學[M].北京: 中國水利水電出版社,2000.
[5]DAVID M Potts, LIDIJA Zdravkovic.Finite element analysisin geotechnical engineering: theory[M].London:Thomas Telford, 1999.

