純物質臨界參數估算方法的研究進展

王小艷，司繼林，張 達，項曙光

（青島科技大學煉油化工高新技術研究所，山東 青島 266042）

進展與述評

純物質臨界參數估算方法的研究進展

王小艷，司繼林，張 達，項曙光

（青島科技大學煉油化工高新技術研究所，山東 青島 266042）

純物質的臨界參數在描述流動相行為、預測物質性質、發展狀態方程等方面都是非常重要的。臨界參數的準確與否直接影響其它物性參數的估算結果。通過建立數學模型為缺少的臨界參數進行預測估算，是人們獲得臨界參數的重要研究途徑。本文對純物質臨界參數的估算方法進行了綜述。主要介紹了其與其它物性相關聯的估算方法、基團貢獻法、基于液體狀態方程的估算方法、定量結構性質關系法（QSPR法）等幾類具有代表性的臨界參數估算方法；并重點闡述了這些方法的原理、應用范圍、優缺點及最近幾年的進展情況；最后指出隨著科學和計算機的快速發展，估算臨界參數的方法也將不斷完善和提高，具有更好的通用性和精確度，進而為化工流程模擬、工程設計計算、科研生產及應用研究提供更加可靠的數據。

臨界參數；估算方法；基團貢獻法；QSPR法

純物質的臨界參數（Tc、Pc、Vc）是重要的化工基礎數據，并廣泛應用于各種物性的估算之中。目前人們花費了大量的精力和時間對臨界參數進行收集、整理和評定，并致力于臨界參數測定方法的研究[1-2]。但由于臨界參數實驗測定困難，至今只測定了幾百種物質的臨界數據[3]，而這些數據大多是穩定物質的，有很多不穩定物質則缺乏實測的臨界數據[4]。因此，為了滿足化工生產、工程設計和科研的需求，就要尋找一些良好的估算方法對物質的臨界參數進行估算。

臨界參數的估算方法很多，具有代表性的主要有4種：與其它物性相關聯的估算方法、基團貢獻法、基于液體狀態方程的估算方法以及定量結構性質關系法（即QSPR法）。其中，基團貢獻法是最重要且應用最為廣泛的方法。近幾年，許多人在已有的估算方法基礎上進行改進擴展，提出了一些其它方法，并對這些方法進行了評估[5-7]。

本文作者闡述了已有的臨界參數估算方法，從中對幾種重要估算方法的研究進展、計算原理、優缺點及應用范圍進行了簡單描述，并重點闡述了幾種最近提出的、在一般著作中很少討論的方法，最后對這些方法進行了簡單的比較和評估。

1 與其它物性相關聯的估算方法

該類方法是利用較為常見的、易于測量的常壓沸點、相對密度、相對分子質量等簡單物性建立關聯式計算臨界參數。1890年，Guldberg[8]最早提出了一個簡單的關聯式Tc=1.5Tb估算臨界溫度；20世紀80年代，Klincew itz-Reid[9]推出了一個較為著名的公式；1994年，周傳光等[10]提出了由化合物的沸點與相對密度推算出有機物臨界性質的關聯式；1999年，馬沛生等[11]提出了使用常壓沸點、相對密度和分子量估算臨界參數的關聯式；2003年，呂玉平等[12]提出了由化合物的正常沸點、常溫相對密度、相對分子質量和分子中原子數估算臨界參數的一組關聯式；2005年，王新紅等[13]提出了使用常壓沸點、相對密度和相對分子質量估算臨界參數的關聯式；2007年，Vejahati和Nikoo[14]也提出了使用簡單物性估算臨界參數的關聯式。

此類估算方法僅需要幾種簡單易測的物性，計算公式和過程都很簡單，估算誤差與基團貢獻法大致相當。在實際使用時，要注意單位是否統一，不統一時需要對物性數據進行簡單的單位換算。

2 基團貢獻法

起初用基團貢獻法估算臨界性質時，基團劃分簡單而粗糙，估算結果不是很好。1955年，Lydersen[15]提出了第一個基團劃分比較細致、估算結果較好的基團貢獻方法。在此基礎上，人們對基團法不斷改進創新，提出了一系列的基團貢獻法，如 Joback[16]、 Ambrose[17]、 Somayajulu[18]、Constantinous和Gani[19]、Wilson和Jasperson[20]、Marrero和Pardillo[21]、梁英華和馬沛生[22]等。這些基團貢獻方法雖然簡單、計算快速，且不需要復雜的計算機計算，但是不能區分同分異構體，并忽視了鍵與鍵之間的相互作用。為了克服這些缺陷，Lymperiadis[23]、Valderrama和Alvarez[24]、Skander和Chitour[25]等都提出了較新的基團貢獻方法，如定位分布貢獻法、元素和化學鍵法、人工神經網絡基團貢獻法等，其中一些方法還擴展到了生物分子領域，應用更加廣泛。

下文從不同影響因素出發，分別以Joback法、Constantinous-Gani法、定位貢獻法、基于元素和化學鍵法和人工神經網絡基團貢獻法（ANN-GC）為例來具體說明基團貢獻方法的估算形式。

2.1 只考慮一級基團影響的方法

較早使用的Lydersen法、Joback法、Fedors法、Ambrose法、Somayajulu等基團貢獻法都是只考慮一級基團影響的方法，具有相似的估算公式和較好的估算精度。馬沛生等選用3種估算方法分別對275種化合物進行計算，平均誤差列于表1。下文以Joback法為例來說明這類方法的計算形式。Joback法的關聯式如式（1）～式（3）。

Joback法計算簡單方便，臨界溫度Tc的精確度取決于正常沸點值Tb是實驗值還是估算值。若是實驗值，Joback法估算得到的所有物質的Tc都很可靠，估算精度高；反之，誤差增大，估算精度降低。該方法對大分子物質的估算值通常過小，對鹵化合物的估算值往往偏大。

2.2 考慮了二級基團影響的方法

Constantinous-Gani法與Joback法相比，該方法加入了二級基團，不僅考慮了基團本身的影響，還考慮了基團間相互作用的影響。C-G法的表達式如式（4）～式（6）。

表1 計算臨界參數平均誤差比較

表2 C-G法、M-P法和L-M法計算臨界參數平均誤差比較

C-G法雖然考慮了二級基團影響因素，估算精度有很大提高，使得估算值更加可靠，但C-G法對很小和很大分子組成的物質估算誤差較大，特別是氟化物和較大分子的環（結構）化合物。而主要問題在于很多物質無法拆分，不能利用C-G法等考慮二級基團的估算方法。

與C-G法相似的方法還有W-J法、M-P法、L-M法等。C-G法、M-P法和L-M法的平均誤差列于表2。由表2可以看出，加上二級基團項后，估算誤差明顯減小。

2.3 定位分布貢獻方法

以上的幾種基團貢獻法都不能區分同分異構體，基于這種背景，Wang和Ma等提出了一個定位分布貢獻方法理論，將該理論成功應用于臨界溫度[26]、臨界壓力[27]、臨界體積[28]等臨界參數的物性計算之中，解決了五十多年來物性計算領域有機物同分異構體無法分辨的這一世界性難題。該方法的特點就是使用添加定位分布因子的定位分布函數來區分大多數有機物cis-和trans-或Z-結構和E-結構的同分異構體。估算臨界參數的定位分布貢獻法函數如式（7）～式（10）。

該方法考慮了定位分布因子的影響，在估算具有同分異構體的有機物時相當可靠。Wang等用不同的實驗數據點對定位分布貢獻法、Joback法和C-G法這3種方法進行比較，所得到的平均誤差列于表3。從表3可知，定位分布貢獻方法具有更高的估算精度。

表3 計算臨界參數平均誤差比較

2.4 基于元素和化學鍵法

荊玉杰和項曙光[29-30]提出了一種基于元素和化學鍵估算有機物臨界參數的貢獻方法。該法是從分子結構理論出發，以元素和化學鍵為基本單位，取代傳統的基團貢獻法中的基團，來考察元素和化學鍵對臨界參數的貢獻。

元素和化學鍵法將元素分為C、H、O、F、Cl、Br、I、N、S，將化學鍵分為環狀和非環狀兩大類，再根據每一化學鍵兩端所連接的原子分成不同的化學鍵，如C—C鍵、C—O鍵、環C—C鍵、環C—O鍵等；考慮到苯環中化學鍵為介于C—C鍵和C=C鍵之間的一種化學鍵這一特殊性，將苯環單列為一個特殊的化學鍵。根據這一理論思想，荊玉杰和項曙光等對9種元素和29種化學鍵進行關聯，提出若干個通用的估算臨界參數的關聯式。他們在大量已知物質的物性基礎之上，對關聯式中的各元素和化學鍵的貢獻值進行回歸，得到關聯式中的參數值，來確定估算關聯式，最終回歸得到4個估算臨界壓力的關聯式和2個估算臨界體積的關聯式，并使用這些關聯式來預測未知物質的臨界壓力和臨界體積。

本方法是基團貢獻法中的一種歸納法，估算關聯式和計算過程都比較簡單，使用也很方便，僅需要化合物的分子結構即可。該法適用范圍較廣，荊玉杰等對極性和非極性、鏈狀和環狀、烷烴和芳香烴、醇、醛等各種物質進行回歸關聯，除了對醛類和酸類的有機物估算誤差較大之外，對于其它有機物質估算精度都比較好，該方法的主要缺點是不能很好地區分同分異構體。

2.5 人工神經網絡基團貢獻法（ANN-GC）

人工神經網絡（ANN）是從生物神經網絡系統的生物神經元（神經細胞）得到啟發而開發出的一種新型的信息處理系統和計算系統。由于人工神經網絡在求解問題時無需事先建立精確的物理模型和數學模型而被應用于物性估算之中。且多層前饋網絡可以逼近任意的連續函數，并與一個微分方程（組）對實際系統的描述能力等價，是一種適用性較強的物性估算方法。國內外有很多人都在研究人工神經網絡在物性估算領域中的應用。曠戈和趙素英等[31]提出了估算有機物臨界參數的人工神經網絡基團貢獻法（ANN-GC），以不同的基團類型和常壓沸點組成為網絡輸入節點，再將臨界溫度、臨界壓力、臨界體積這3個臨界參數作為網格輸出。Gharagheizi等[32-33]通過使用人工神經網絡基團貢獻法對DIPPR801數據庫的純物質進行預測，獲得一個精度較好的估算結果，所測得臨界參數的平均相對誤差分別為0.9%、1.1%、1.4%。

人工神經網絡的發展主要經歷了早期工作階段、過渡期階段、復蘇階段和成熟理智階段這4個階段。ANN-GC法的形成過程并不復雜，首先是尋找化合物官能團和所期望物性之間的關系。而完成這一重要步驟最簡單的方法就是假設基團和期望物性（臨界性質）之間存在一個多線性關系，這與典型的基團貢獻方法相似。但是在使用那些簡單的估算方法解決現存的問題時，結果往往不是很好。因此，可以優先考慮人工神經網絡法這個非線性數學方法解決比較繁瑣的問題。研究這些復雜的系統需要有很多強大的數學工具，如使用MATLAB軟件中的ANN工具箱和FFANN（三層前向人工神經網絡）。

人工神經網絡具有基本結構單一性、大量單元互耦性、存儲記憶聯想性、處理信息并行性、獲取知識自學習性、模式識別性能、外推性和信息容錯性、處理非線性問題良好等諸多的優點。且該方法與數學回歸方法不同，是通過不斷地篩選與增加更可靠的數據而提高預測的可靠性，利用其處理非線性數據、識別模式、自組織、自學習等能力可以解決很多傳統方法難以解決的、比較繁瑣的問題。但是人工神經網絡也存在一些局限性，如訓練時間長、需大量訓練數據、不能保證最佳結果、不能保證完全可靠。隨著計算機技術的飛速發展，人工神經網絡在化學工程領域的應用研究相當活躍。它被廣泛應用于各種科學和工程研究之中，在估算純物質物性方面有很好的應用前景。

2.6 小結

通過以上幾種基團貢獻方法可知，根據分子結構中各個基團所作貢獻的加和這一原理，每類方法具有相似的估算公式。只考慮一級基團影響的方法，基團劃分比較簡單，估算公式簡潔，計算簡單易行，估算精度良好。考慮二級基團影響的方法，與只考慮一級基團的貢獻法相比，計算結果更好，計算精度更高，但是由于許多物質不能拆分，而無法對其進行估算。Wang等[26-28]提出的定位分布貢獻法在估算有機物同分異構體時，比一般的方法都要準確穩定，具有很高的預測精度。元素和化學鍵法僅以單個元素和化學鍵為單位，結構拆分更加簡單，計算過程也不復雜，但不能區分同分異構體。人工神經網絡基團貢獻法在解決非線性問題時具有較高的估算精度。

3 基于液體狀態方程的估算方法

基于液體狀態方程的估算方法是根據其它物性的半經驗關聯式而提出的一種估算方法。該方法計算復雜，估算需用的物性參數多，通用性不好，一般不常用。該方法是結合一種特殊的PVT關系而建立的臨界性質間的相互計算。此法是由意大利學者Vetere首先提出的，下面是以Rackett方程[34]為基礎而提出的估算公式，見式（11）～式（13）。

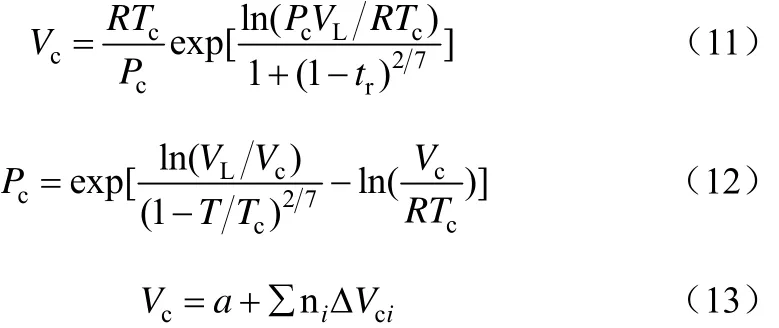
該法首先用基團貢獻法求出臨界體積Vc，再利用已知兩個溫度下的飽和體積聯立求解，可得Tc、Pc，最后將得到的Tc和Pc的值代回式（12）求出Vc。后來，Vetere又以Spencer方程[35]為基礎，提出了另一個與上述計算式相似的方法。這兩種方法的計算精度與Lydersen方法相當，但所求臨界參數對采用的密度值可靠性十分敏感，不適用于締合或二聚的化合物如醇類、酸類的計算。為了克服這些缺陷，Vetere又提出了一個新的計算方法，即引入極性參數，只使用一個密度數據，對每類化合物都給出其計算式。這些計算式過于繁瑣，仍不適用于多基團化合物。

4 定量結構性質關系法

定量結構性質關系法（QSPR法）是由物質的微觀結構特征來估算宏觀物性的一種方法。它主要應用統計學和理論計算的方法研究化合物的分子結構與其物理和化學性質之間的定量關系，具有較好的估算精度，是目前物性估算領域的新方法，也是今后物性估算領域的研究熱點之一。

目前致力于臨界參數的定量結構性質研究較少。國內外的一些專家和學者將QSPR的研究方法應用到臨界參數的估算領域中，解決了很多實際問題，并得到了令人滿意的結果。如李士雨和闕慧玲[36]采用分子模擬和多元線性回歸方法研究了有機物臨界體積的定量結構性質關系；聶長明等[37]對烷烴類臨界參數的定量結構性質關系進行了研究。Godavarthy等[38]對純物質進行預測并提出了一個QSPR模型來估算臨界參數；Sola等[39]也提出了一個估算臨界參數的QSPR模型。這些模型能夠快速有效地對未知化合物的性質進行預測，并在分子結構的基礎上對物質的差異的理論依據進行討論，對合成高效化合物的實驗給予理論指導。

定量結構性質關系法（QSPR）也稱分子描述子法。QSPR法是以分子性質（分子特征因子）為基礎的，估算時需要依賴于強大的計算機軟件來獲得在線的分子結構和分子性質，再使用量化的結構性質（QSPR）關系式來估算宏觀性質。該法的關鍵是分子描述子的選擇和數學模型的建立，分子描述子在分子結構的質量描述中起著很大作用，其目的是創建一個物理化學性質的數字化尺度，用于尋找更適當的預測模型。目前分子描述子的個數已有二百多個，維數從二維延伸到三維甚至更多，使用方面也不再單一。根據描述的內容不同，可把描述符分為組成描述符、拓撲描述符、幾何描述符、靜電描述符、量子化學描述符和熱力學描述符這6類。建立穩定、可靠的數學建模方法也越來越多，常用的建模方法主要有啟發式方法（HB）、最佳多元線性回歸（BMLR）、徑向基函數神經網絡（RBFNN）、支持向量

機（SVM）、遺傳算法等。建立QSPR模型的目的是為了預測新的化合物的性質，因此預測能力是QSPR模型評價的一個重要指標。內部驗證法和留一法交互驗證法是兩種很好的估計模型預測能力的方法。

隨著計算機分子描述符方法和一些新近統計學方法的發展，計算得到的各種理論結構的描述符可以全面地描述分子的結構特征，人工神經網絡和支持向量機的應用更好地促進了QSPR的快速發展，使得QSPR的研究領域從單一的有機化合物的理化性質發展到化學中的材料、分離和環境等方面。定量結構性質法的優點是不一定依賴實驗數據、預測較為準確、可用于含有復雜基團的、非穩定物質以及混合物系。由于需要借助于分子特征因子計算程序，所以QSPR模型進行實際估算時受到計算資源的限制。

5 其它預測方法

除了以上幾種方法外，估算臨界參數的方法還有臨界指數計算法、半理論的方法、立方型狀態方程法等。

臨界指數計算法指在臨界點的某一小領域即臨界區內，用冪指數的形式表示某些熱力學量間的關系，這些冪指數被稱為臨界指數，臨界指數的計算以平均場理論為依據，根據汽液相變臨界現象的指數律和標度律進行。目前國內外有很多專家學者做這方面的研究，希望能提出系統的臨界指數用于估算臨界參數。

隨著量子化學的發展，量子理論廣泛應用于結構和性質關系之中，而理論計算可以得到結構和性質研究中所需要的數據。半理論的預測方法首先是理論計算出所需數據，再計算出適合的描述子，從而建立數學模型以預測臨界性質。該方法可用于預測復雜純物質的臨界性質，估算精度較高，有較好的應用前景。

立方型狀態方程在相平衡計算中的準確性較好，被廣泛應用于工業之中。無論是對純物質還是混合物，立方型狀態方程都與純物質的臨界性質緊密相關，通過立方型狀態方程來獲得臨界參數也是人們的研究方向之一。Hsieh和Lin[40]、Twu[41]等都提出了不同的立方型狀態方程來估算臨界性質。朱慶莉等[42]提出了一個使用四次立方型狀態方程來估算臨界性質的新方法。這類方法需要一些實驗數據點，包括溫度、飽和蒸汽壓、飽和液體摩爾體積和蒸發焓。對大多數物質來說，這些實驗數據在正常溫度下就很容易測得。該方法對于那些不知道分子結構的化合物具有很大的使用價值，但是估算精度不是很高。

6 結語與展望

綜上所述，臨界參數估算方法已經有了很大進展，但并不是每種方法都適用于估算各種類型的物質物性。有一些方法具有一定的針對性和局限性，科研人員要根據實際需要來選擇計算簡單、估算精度較高的方法。

基團貢獻法應用最為廣泛，發展速度最快，也是人們研究重點之首。基團貢獻法的優越性在于它的普遍性，從理論上來說，只要官能團的參數完備，它就能計算任何體系的性質。但由于基團貢獻法中的官能團參數是用不完全的實驗數據擬合出來的，擬合過程中又會丟失部分信息，所以官能團參數不可能對一切物系都準確，因而基團貢獻法的計算結果與實際情況往往有較大的差距。針對這些問題，可以從兩個方向對基團貢獻法進行改進，不斷提高其計算精度以及在計算機中的應用效率。第一個方向是不斷完善實驗數據和改進數值擬合方法來提高精度；第二個方向是通過研究原子、官能團以及分子之間的相互作用機制來改進基團貢獻法。基團貢獻法發展的前景主要從基團貢獻法與分子模擬、分子熱力學這兩個角度出發。而定位分布貢獻法已成為現今化工數據估算前沿領域最穩定、最廣義、最準確的計算方法。

與其它物性相關聯的估算方法僅需要知道物質的幾種物性就可以簡單快捷地計算出臨界參數，但是該類方法要建立在已有的實驗數據之上，其預測精度不是很高。定量結構性質法雖然對計算機的依賴性較強，但它不依賴實驗數據，無論是純物質還是混合物它都能進行估算，且估算值較為準確，通用性較好。隨著計算機技術和量子化學理論的進一步發展，QSPR法也是目前估算臨界參數的研究熱點之一。

隨著科學和計算機的快速發展，估算臨界參數的方法也將不斷完善和提高，具有更好的通用性和精確度，進而為化工流程模擬、工程設計計算、科研生產及應用研究提供更加可靠的數據。

符 號 說 明

Ai——基團i的貢獻值

Aj——基團j的貢獻值

a——常數

a1，a2——模型參數

d420——293.15 K下液相的相對密度

M——相對分子質量

NA——分子中的原子總數

Ni——基團i的總數目

Nj——基團j的數目

P0——124.843 MPa下的壓力

Pc——臨界壓力，MPa

Pk——定位分布因子

ΔPi——基團i的臨界壓力貢獻值

ΔPj——基團j的臨界壓力貢獻值

T0——7409.200 K下的溫度

Tb——正常沸點，K

Tc——臨界溫度，K

ΔTi——基團i的臨界溫度貢獻值

ΔTj——基團j的溫度貢獻值

tr——對比溫度

V0——1011.117 cm3/mol下的體積

Vc——臨界體積，cm3/mol

ΔVi——基團i的臨界體積貢獻值

ΔVj——基團j的臨界體積貢獻值

[1] 張紅彥，馬沛生．臨界參數的估算方法[J]．化學工業與工程，2000，17（3）：149-154．

[2] Kazakov A，Muzny C D，Diky V，et al. Predictive correlations based on large experimental datasets：Critical constants for pure compounds[J]．Fluid Phase Equilib.，2010，298：131-142．

[3] 馬沛生，等．石油化工基礎數據手冊續編[M]．北京：化學工業出版社，1993．

[4] 高進．不穩定物質臨界參數測定[D]．天津：天津大學，1999：44．

[5] Su Y C，Liu Y A，Diaz Tovar C A，et al. Selection of prediction methods for thermophysical properties for process modeling and product design of biodiesel manufacturing [J]．Ind．Eng．Chem．Res．，2011，50 （11）：6809-6836．

[6] Garcia Manuel A lba Juan-Jose，Gonzalo A lberto，et al. Comparison of methods for estimating critical properties of alky esters and its mixtures[J]．J．Chem．Eng．Data，2012，57：208-218．

[7] 伍科，鄧文生，賈冬梅．有機物臨界性質預測方法研究的進展[J]．計算機與應用化學，2009，26（1）：125-128．

[8] Reid R C，Sherwood T K．The Properties of Gases and Liquids [M]．New York：M c Graw-Hill，1958．

[9] K lincew itz K M，Reid R C．Estimation of critical properties w ith group contribution methods[J]．AIChEJ.，1984，30（1）：137．

[10] 周傳光，楊福勝，胡仰棟，等．由化合物的沸點及比重推算臨界參數[J]．計算機與應用學，1994，11（2）：123-126．

[11] 馬沛生，肖劍. 酯、醚臨界參數的推薦值和質量碼[J]．石油化工，1999，28（1）：32-35；化工進展，1999，18（s1）：222．

[12] 呂玉平，許旋，彭彬，梁堯．有機物臨界參數的關聯式估算研究[J]．計算機與應用化學，2003，20（5）：709-712．

[13] 王新紅，賈琦，高進，等．用簡單物性估算純物質臨界參數的方法[J]．石油化工，2005，34（3）：254-257．

[14] Vejahati F，Nikoo M B．Simple correlation estimates critical properties of alkanes[J]．Pet．Sci．Technol．，2007，25：1115-1123．

[15] Lydersen A L．Estimation of Critical Properties of Organic Compounds[M]．Madison：Univ Wisconsin Eng Exp Sta Rept 3， 1955．

[16] Joback K G，Reid R C．Estimation of pure-component from group contributions[J]．Chem.Eng.Commun.，1983，57：233-237．

[17] Ambrose D．Correlation and Estimation of Vapor-Liquid Critical Properties：Critical temperatures of organic compounds．Npl. Rep. Chem. 92[R]．Nat. Phys. Lab.，UK，1978．

[18] Somayajulu G R．Estimation procedure for critical constants [J]．J．Chem．Eng．Data，1989，34：106．

[19] Constantinou L，Gani R．New group contribution method for estimating properties of pure compounds[J].AIChE.J.，1994，40（10）：1697-1710.

[20] Wilson G M，Jasperson L V．Critical constantsTcandPc，estimation based on zero，first and second order methods[C]//Paper given at AIChE Spring National Meeting，New Orleans，LA，USA，February 25-29，1996．

[21] Marrero-Morejon J，Pardillo-Fontdevila E．Estimation of pure compound properties using group-interaction contributions[J]．AIChE J.，1999，45：615-621．

[22] Liang Yinghua，Ma Peisheng．A new group-contribution method for critical properties[J].Chinese J．Chem．Eng．，2000，8：74．

[23] Lymperiadis A，Adjiman C S，Jackson G，et al. A generalisation of the SAFT-gamma group contribution method for groups comprising multiple spherical segments[J]．Fluid Phase Equilib．，2008，274：85-104．

[24] Valderrama J O，Alvarez V H. A new group contribution method based on equation of state parameters to evaluate the critical properties of simple and complex molecules[J]．Can．J．Chem．Eng．，2006，84（4）：431-446．

[25] Skander N，Chitour C E. Group-contribution estimation the critical properties of hydrocarbons[J]．Oil Gas Sci．，2007，62：391-398．

[26] Wang Q，Ma P S，Jia Q Z，et al. Position group contribution method for the prediction of critical temperatures of organic compounds[J]．J．Chem．Eng．Data，2008，53：1103-1109．

[27] Wang Q，Jia Q Z，Ma P S．Position group contribution method for the prediction of critical pressure of organic compounds[J].J．Chem．Eng．Data，2008，53：1877-1885．

[28] Wang Q，Jia Q Z，Ma P S．Position group contribution method for the prediction of critical volume of organic compounds[J].J．Chem．Eng．Data，2008，53：2606-2612．

[29] 荊玉杰，項曙光．估算有機物臨界壓力的元素和化學鍵貢獻法[J]．石油化工，2004，33（7）：636-641．

[30] 荊玉杰，項曙光．基于元素和化學鍵的臨界體積估算新方法[J]．青島科技大學學報[J]．2004，25（5）：397-401．

[31] 曠戈，趙素英，趙之山，王良恩．人工神經網絡基團貢獻法估算純有機物的臨界參數[J]．計算機與應用化學，2001，18（4）：396-399．

[32] Gharagheizi Farhad，Eslam imanesh A li，Mohammadi Am ir H，et al. Determ ination of critical properties and acentric factors of pure compounds using the artificial neural network group contribution algorithm[J]．J．Chem．Eng．Data，2011，56：2460-2476．

[33] Gharagheizi F，Eslam imanesh A，Mohammadi A H，et al. Determ ination of parachor of various compounds using artificial neural network-group contribution approach[J].Ind. Eng. Chem. Res.，2011，50（9）：5815-5823．

[34] 張紅彥，馬沛生．Raekett方程推算臨界參[J]．計算機與應用化學，1997，14（s1）：319．

[35] Spencer C F，Danner R P. Improved equation for predictions of saturated liquid density[J]．J．Chem．Eng．Data，1972，17：236．

[36] 李士雨，闕慧玲，等．有機物臨界體積的定量構性[J]．化學工業與工程，2007，24（2）：134-138．

[37] 聶長明，戴益民，文松年，等．烷烴類臨界參數的定量構效關系研究[J]．武漢理工大學學報，2005，27（8）：1-4．

[38] Godavarthy S S，Robinson R L J，Gasem K A M．Improved structure-property relationship models for prediction of critical properties[J]．Fluid Phase Equilib．，2008，264：122-136．

[39] Sola D，Ferri A，Banchero M，et al．QSPR prediction ofN-boiling point and critical properties of organic compounds and comparison with a group-contribution method[J]．Fluid Phase Equilib．，2008，263：33-42．

[40] Hsieh C M，Lin S T．Determ ination of cubic equation of state parameters for pure fluids from first principle solvation calculation[J]．AIChE J．，2008，54：2174-2181．

[41] Twu Chorng H．A novel theory for predicting critical constants and the function for pure polymers[J]．Ind．Eng．Chem．Res．，2010，49：11801-11808．

[42] Zang Lianyun，Zhu Qingli，Yun Zhi．Critical properties prediction based on a quartic equation of state[J]．Can．J．Chem．Eng．，2010，88：1003-1009．

Research progress of estimation methods for critical parameters of pure substances

WANG Xiaoyan，SI Jilin，ZHANG Da，XIANG Shuguang
（Hi-Tech Institute for Petroleum and Chem ical Industry，Qingdao University of Science and Technology，Qingdao 266042，Shandong，China）

The critical parameters of pure substances are very important in describing fluid phase behavior，predicting their properties，and developing the equation of state．The accuracy of critical parameters directly affects the estimation of other parameters. Through establishing the mathematical model for a lim ited number of critical parameters is an important research approach to obtaining critical parameters．A variety of estimation methods for critical parameters of pure substances are summarized，including the method of correlating the critical parameters w ith other properties，group contribution method，method based on liquid equation of state，quantitative structure property relationship (QSPR) method and several types of representative estimation methods of critical parameters are discussed in terms of principles，application ranges，advantages and disadvantages，and development in recent years．The development trend of the methods for estimation of critical parameters is discussed．

critical properties；estimation method；group contribution method；QSPR method

TQ 013.1

A

1000–6613（2012）09–1871–07

2012-03-05；修改稿日期：2012-05-02。

王小艷（1987—），女，碩士。E-mail wxy.2007.hi@163.com。聯系人：項曙光，博士生導師。E-mail xsg@qust.edu.cn。