投資組合模型的動態規劃解法

陳國華，廖小蓮,吳 娜

(湖南人文科技學院 數學系,湖南 婁底 417000)

0 引言

投資組合選擇在企業經濟活動中有著重要的指導作用。Markowitz[1]的均值方差理論為近代證券投資組合理論奠定了基礎。而均值方差模型的實質上是一個以二次規劃優化模型。為了減少參數、簡化計算，不少文獻[2，3]提出了線性化投資組合模型，但是，將一定數量的資金有選擇地投入多種產業，可以作為一個多階段決策過程，即動態規劃模型。利用動態規劃研究投資組合問題的方法已有一些研究[5，6，7]。在文[5]中，作者對均值－方差模型建立一種動態規劃模型和遞推算法。文[6]對多階段資產投資問題，給出了在滿足一定的風險承受能力情況下的、以總收益盡可能大為決策目標的資產投資組合模型，利用動態規劃方法求得多階段投資的最優投資組合，文[7]引導投資者選擇最佳投資策略,將動態規劃模型應用于組合投資理論，文[8]在允許賣空的情況下,以終端財富最大化為目標,通過建立輔助問題,利用逆序動態規劃的求解方法，文[9]利用動態規劃方法解決帶交易費用的均差模型,給出了有交易費用均差模型的解析解。

1 投資組合模型模型的建立

設有資金M，可在一個時期內投資于市場上的n種資產A1,A2,…,An或存款銀行A0，用指標凈收益盡可能大與總風險盡可能小來衡量投資方案的優劣，假定通過統計分析，得到各資產Ai的平均收益率為ri，與風險損失qi。銀行存款A0的利率為r0且無風險(q0=0)。購買資產Ai的交易費是分段函數：收費率為 pi，但當購買量不足ui時，交易費按購買ui計算。因此，購買Ai的收益須減去交易費之后得到凈收益。在本文中，我們以投資各個Ai的風險損失和來度量總體風險。設xi表示購買資產Ai的資金(1 ≤i≤n)，x0為銀行存款。則交易費可表為：

在本文中我們利用線性加權法把雙目標規劃問題轉化為單目標規劃問題。考慮到風險的特殊性，我們附加一個約束從而得到如下的投資組合模型：

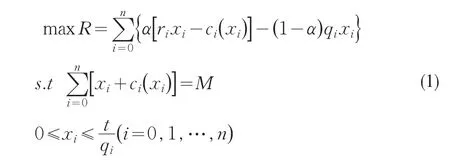
其中t為參變量。由于ci(xi)是分段線性函數(在xi=0處不連續)，模型為非線性規劃問題，下面我們利用動態規劃來求解。

2 模型的動態規劃解法

在模型（1）中，對n+1種資產的資金分配看成n+1階段決策過程，其中xi作為第i階段的決策變量，從第0階段到第i階段所分配的資金，記為si，作為第i階段的狀態變量。那么，n+1階段所分配的總資金為si=M，且狀態轉移規則為：

當狀態變量si給定時，決策變量xi的取值范圍稱為第i階段的決策集，記為Di()Si。根據上面的模型，我們有：

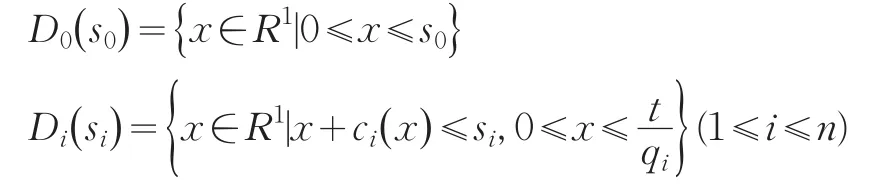
在每一階段決策時都要求xi∈Di(si)。這樣一來，靜態模型(1)就轉化為一個動態決策過程。

2.1 動態規劃算法

根據前面的分析，總資金M作為第n+1階段的終止狀態，我們利用動態規劃的順推算法來求解。設最優值函數fk(s)=直到第k階段投資金額不超過s的最大收益，得到：

根據動態規劃的最優化原理，得到最優值函數序列滿足的遞推方程如下：

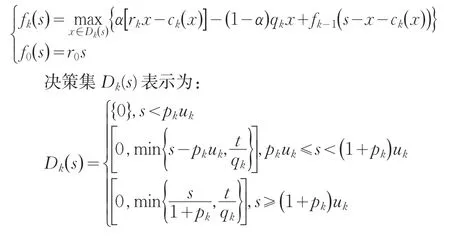
3 數值算例

假使經過統計分析，決策者已獲得了如下的數據(見表1)。

表1

i可以不考慮起點金融ui，那么它就可以用線性函數pix 來代替。）

首先將M離散化，插入分點0，0.5，1，1.5，2=M

進行回代，得出最優解：

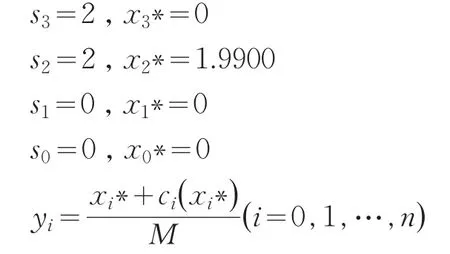
得到最優投資組合(y0,y1,y2,y3)=(0 ,0,1,0 )，即：向A2投資200萬元。

4 結束語

投資組合是現實社會的一個廣泛而重要的課題，本文主要探討了將動態規劃最優性原理應用于投資組合的研究，針對資金分配、資產投資及多目標資產投資建立了數學規劃模型，利用動態規劃對問題進行了求解，數值算例說明了模型的可行性，對指導投資決策具有一定的知道意義。

[1]Markowitz.H.M.Portfolio[J].Journal of Finance,1952,(7).

[2]陳煒,楊玲.具有交易費用的均值一極大極小半絕對偏差投資組合模型[J].首都經濟貿易大學學報,2009,(6).

[3]陳國華,廖小蓮.基于區間規劃的投資組合模型[J].遼寧工程技術大學學報(自然科學版),2010,29(5).

[4]丁元耀,賈讓成.一種證券組合的投資選擇建模[J].運籌與管理,1999,8(2).

[5]林浩,投資組合問題的動態規劃方法[J].運籌與管理,2000,9(3).

[6]宿潔,劉家壯.多階段資產投資的動態規劃決策模型[J].中國管理科學,2001,9(3).

[7]伍勇,劉春.動態規劃模型在“組合投資”理論中的應用[J].北京機械工業學院學報,2008,23(2).

[8]孫世杰,高巖.摩擦市場下多階段投資組合的均值方差模型[J].上海理工大學學報,2008,30(4).

[9]花秋玲,蘇孟龍,呂顯瑞,王銳.帶交易費用投資組合問題的動態規劃方法[J].吉林大學學報(理學版),2009,47(5).