基于最短路徑樹的分布式功率控制路由算法*

陳友榮，任條娟，劉半藤，葛靈曉

(浙江樹人大學信息科技學院，杭州 310015)

無線傳感網通常有一個重要目標——延長網絡生存時間。由于大部分情況下所有節點的能量有限，不能補充和更換，一旦節點能量耗盡，該節點就會失效，這將影響到網絡的運行，甚至可能導致網絡的癱瘓，因此延長網絡生存時間可以節省重新部署無線傳感網的巨大開銷［1］。

目前，無線傳感網路由的研究已取得一些成果。文獻［2－3］用分布式的線性規劃公式表示路由問題，采用對偶分解和次梯度方法求解最優路由方案，最大限度提高網絡生存時間，但是用最優化方法研究路由方案的算法復雜，很難在實際硬件環境中實現。文獻［4］提出LET(Least Energy Tree)算法。它是根據dijkstra算法構建每個節點到Sink節點能耗最小的最短路徑樹，最終所有節點沿著最短路徑樹將數據發送給Sink節點。文獻［5］在LET算法的基礎上提出了“比例權值路由算法”Ratio_w(Ratio Weight Routing Algorithm)與“和權值路由算法”Sum_w(Sum Weight Routing Algorithm)。文獻［6］提出多樹路由，在數據發送過程中從多個樹路徑中選擇當前合適的路徑，最終平衡節點能耗，提高網絡生存時間。上述路由算法都假設Sink節點能獲得整個網絡拓撲信息或者節點能獲知與鄰居節點的距離，而且節點可根據與鄰居節點的距離自動調整發送功率，從而減少鏈路能耗。如果Sink節點要得到整個網絡拓撲信息或者節點要獲知與鄰居節點的距離，可通過以下兩種方法實現。第1種方法是添加額外硬件模塊，如配置GPS模塊收集每個節點的位置坐標，或者采用超聲波、紅外等模塊測量節點間距離，通過定位方法計算每個節點的位置坐標。第2種方法是不需要添加額外的硬件模塊，根據節點間通信的RSSI值，估計兩個節點的距離，通過3邊定位等定位算法獲得網絡節點位置坐標。第1種方法需要添加額外硬件，增加了無線傳感網的硬件成本。第2種方法在實際環境中，尤其是在惡劣環境中，RSSI的測量誤差非常大，很難準確測量兩個節點間距離。

考慮到通過兩節點間距離(即通信距離)調整節點發送功率不總是可行的，尤其當節點不增加無線傳感網硬件成本而且節點很難獲知與鄰居節點的距離時，針對此類網絡樞紐節點能量消耗過快而過早失效，從而減少網絡生存時間的問題，提出基于最短路徑樹的分布式功率控制路由算法DPCRA_SPT(Distributed Power Control Routing Algorithm Based on Shortest Path Tree)。當節點很難獲知節點到鄰居節點的距離時，該算法隨著節點剩余能量的減少而自動調整節點發送功率，從而調整整個網絡的拓撲結構。DPCRA_SPT算法還綜合考慮網絡中傳輸數據的能耗、鄰居節點的剩余能量，引入分布式算法的權值函數。每個節點利用分布式非同步Bellman-Ford算法構建最短路徑樹。最終，數據沿著當前網絡拓撲結構下的最短路徑樹匯聚到Sink節點。

1 系統假設

在DPCRA_SPT算法中，假定傳感節點(簡稱節點)隨機分布在一個正方形區域內，周期性地采集周圍環境信息，并假設如下:

(1)Sink節點和所有傳感節點位置固定不變，都是靜止的，而且Sink節點不能獲知整個網絡拓撲結構信息；

(2)所有傳感節點具有相同的性能(如初始能量、能耗參數、無線電最大發送功率、最大通信半徑等)；

(3)所有傳感節點采用統一的能量模型；

(4)所有傳感節點都能感知數據，并通過直接或多跳的方式將數據發送給Sink節點；

(5)每個傳感節點能量受限，但Sink節點能量不受限制；

(6)所有傳感節點沒有安裝GPS等模塊，無法獲知自身的位置坐標，也無法獲知節點到鄰居節點的距離。

2 鏈路能耗模型

常見的鏈路傳輸模型是根據發送節點與接收節點之間距離的Friss自由空間模型和多徑衰弱模型。如果發送節點與接收節點之間的距離小于交叉距離dcrossover，則使用Friss自由空間模型(d2衰減)。如果發送節點與接收節點之間的距離大于或等于交叉距離dcrossover，則使用兩線地面傳播模型(d4衰減)［7］。交叉距離dcrossover的定義如下:

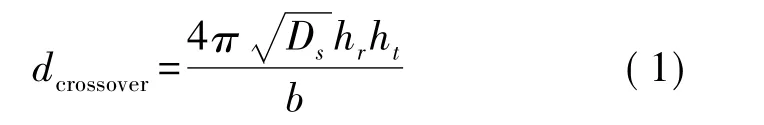
其中Ds≥1，與無線傳播的數據丟包率有關，hr與發送節點的天線高度有關，ht與接收節點的天線高度有關，b代表電磁波的波長。采用根據無線通信能量消耗模型部分參數如下:全向天線，ht=hr=1.5，系統丟失率Ds=1［7］，而且無線傳感網通常采用2.4GHz的無線信號，b=0.125 m，可得dcrossover=226 m。由于交叉距離已經大于一般無線傳感網節點的通信距離，因此鏈路能耗模型選擇Friss自由空間模型，其發送功率和通信距離的關系如下

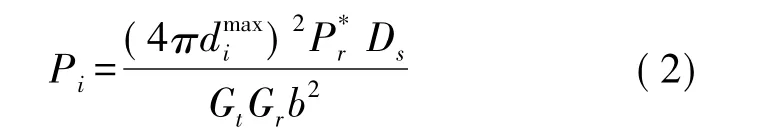
式中:Pi是發送節點i的發送功率，是接收節點的最小接收功率，是節點i選擇發送功率Pi時的最大通信距離。當節點i采用最大發送功率發送數據時，節點j能接收到該數據包，則節點j是節點i的鄰居節點，即j∈N(i)，其中N(i)表示節點i的所有鄰居節點集合。

典型的無線傳感網節點能耗主要由無線數據收發產生［8］。節點發送模塊的能耗ETx由發送電路電子能耗ETx-elec和信號放大器部分的電子能耗ETx-amp組成。節點發送模塊能耗中的發送電路電子能耗ETx-elec和接收模塊中的能耗ERx，固定為gEelec，其中g代表所發送或接收的數據量。信號放大器部分的電子能耗大小與發送功率Pi有關。鏈路能耗模型計算公式改為:

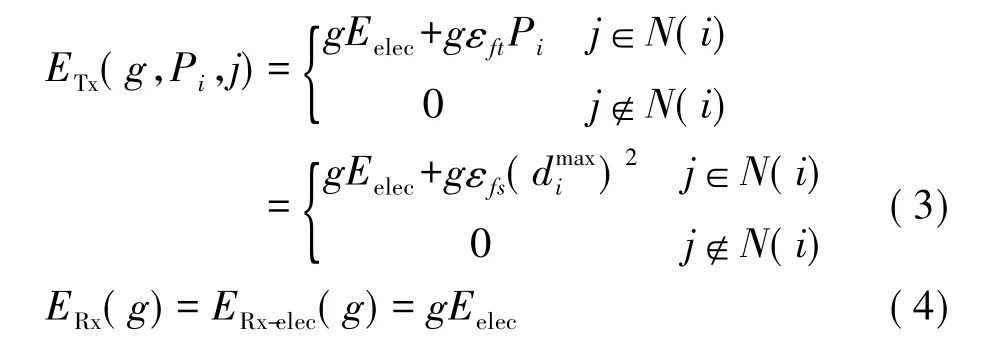
根據式(3)和式(4)可知:傳感節點i與節點j之間傳輸g比特數據的能耗取為:

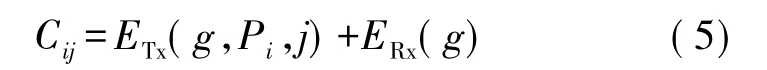
傳感節點i與Sink節點之間傳輸g比特數據的能耗取為:

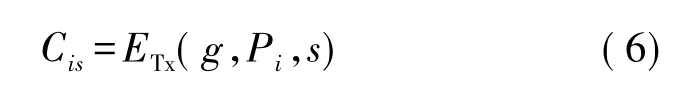
3 算法的原理

通常把計算從源節點到目的節點的最短路徑權值稱為單源最短路徑問題。目前，解決單源最短路徑的方法有很多，分布式非同步Bellman-Ford算法是其中的一種實現簡單的分布式算法［9］。

該算法在利用分布式非同步Bellman-Ford算法尋找最短路徑問題前需要解決以下兩個問題。

第1個問題是鏈路權值的設定會影響網絡的生存時間。考慮到DPCRA_SPT算法是分布式算法，每個節點發送數據前需要根據周圍局部信息選擇鄰居節點，但是節點自身剩余能量不影響鄰居節點的選擇，因此DPCRA_SPT算法簡化鏈路權值，只考慮鏈路能耗(式(5)和(6))和鄰居節點的剩余能量，路由應該選擇鄰居節點剩余能量大而且鏈路能耗小的鄰居節點發送數據。以Re(i)表示節點i的剩余能量，以Cij表示鏈路L(i，j)的能耗，以wij表示鏈路L(i，j)的權值。在DPCRA_SPT算法中，取

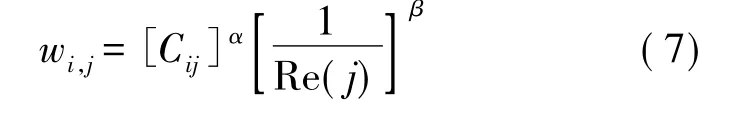
其中α是“能耗因子”，β是“接收剩余能量因子”，而且這兩個因子都是正常數。

第2是如何根據當前局部信息，調整節點發送功率，從而改變網絡的拓撲結構，其具體算法見下一節功率控制算法。

確定節點的發送功率后，即網絡拓撲結構確定，DPCRA_SPT算法采用分布式非同步Bellman-Ford算法找到一顆樹根在Sink節點的最短路徑樹。所有節點沿著最短路徑樹，將數據傳送到Sink節點，從而各個節點均以最小能耗將數據發送到Sink節點。

3.1 功率控制算法

由于節點不能獲知與鄰居節點的距離，但是節點可獲知自身剩余能耗信息，因此DPCRA_SPT算法根據節點剩余能量調整發送功率，改變網絡的拓撲結構，避免該節點能量過早消耗而死亡。如圖1所示，網絡剛開始運行時，1號節點的剩余能量充裕，發送功率大，它可與實線內的所有節點(2～8號節點)通信，與其它節點組成到Sink節點的數據發送路徑，較多的參與數據路由；隨著節點剩余能量的減少，1號節點為避免能量過快消耗，減少自身發送功率，只能與虛線內的節點(2～5號節點)通信；當1號節點的發送功率降到最小要求功率(能與距離最近的2號節點通信的最低發送功率)時，不再改變其發送功率。如果網絡中樞紐節點能量消耗過快，該方法減少發送功率，減少能量消耗，因此能提高網絡的生存時間［10］。

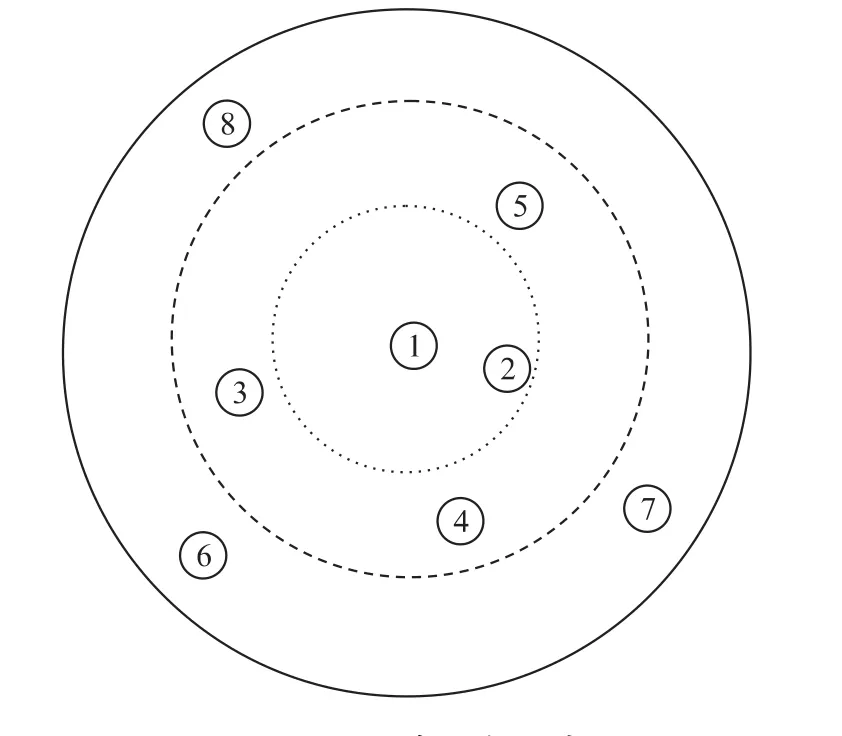
圖1 發送功率調整示意圖

由上述內容可知，DPCAOL_SPT算法調整節點的發送功率，改變網絡拓撲結構，以下給出具體的發送功率衰減模型。圖2是節點發送功率隨著剩余能量變化的線性功率衰減曲線圖。定義［0－1］區間的兩個參數 γl1和 γl2，如圖 2所示，F點位置是(γl1Emax，γl2(Pmax－Pmin(i))+Pmin(i))，功率衰減曲線主要是經過F點的兩條線段組成。每個節點根據剩余能量和衰減曲線，改變節點發送功率。

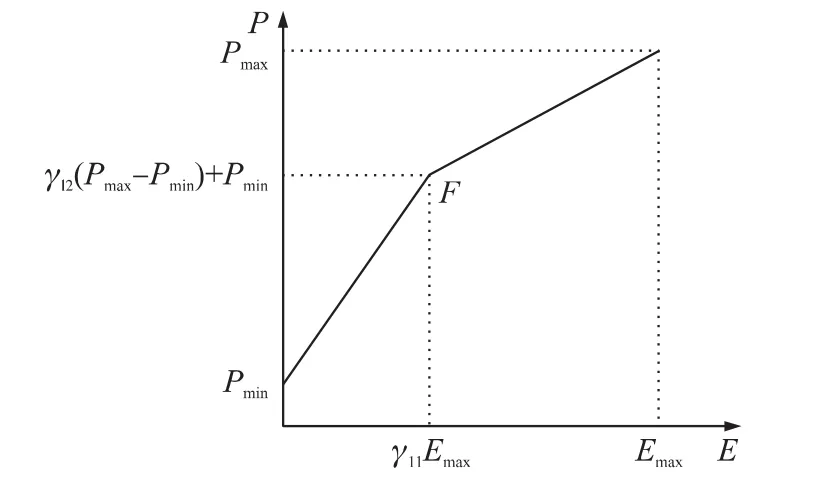
圖2 線性功率衰減曲線

從式(8)可知，線性衰減可出現3種情況。當γl1=0時，F點在x=0的縱坐標上，該節點衰減的曲線是經過(Emax，Pmax)和F點的線段。當γl1=1時，F點在x=Emax的縱坐標上，該節點衰減曲線是經過(0，Pmin(i))和F點的線段。當0＜γl1＜1時，該節點衰減曲線由兩條線段組成，分別是經過(Emax，Pmax)和F點的線段和經過(0，Pmin(i))和F點的線段。

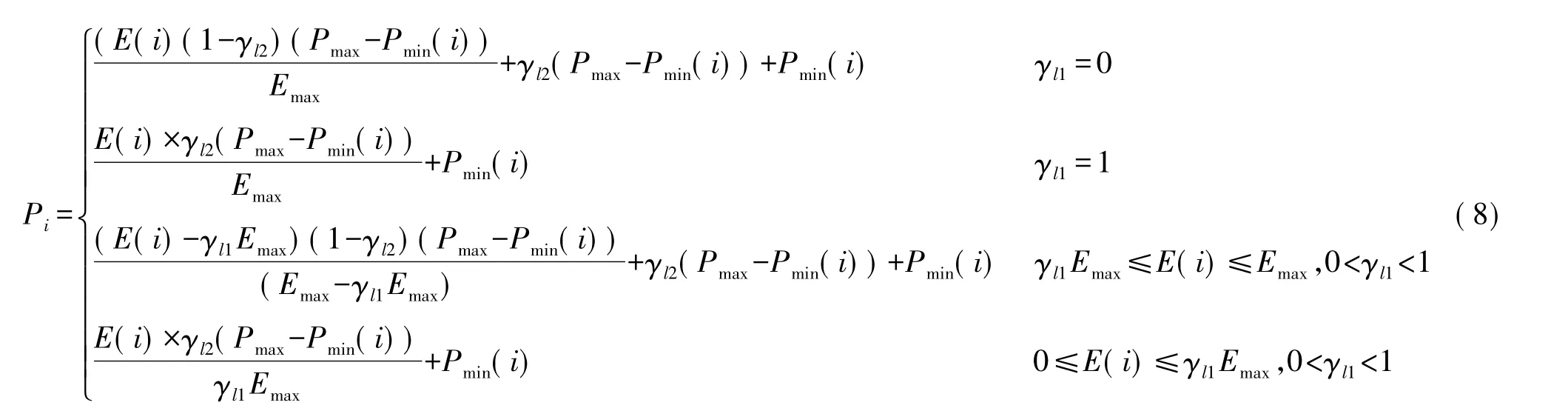
4 算法的實現

提出的DPCRA_SPT是一種分布式功率控制算法。每個節點根據剩余能量調整發送功率，接收鄰居節點信息，采用分布式Bellman-Ford算法找到到Sink節點的最優路徑，具體的實現步驟如下:

第1步 網絡啟動時，節點為了獲知與鄰居節點通信的最低發送功率，其發送功率從0 W開始遞增發送Hello信號。鄰居節點第一次收到該節點的Hello數據包，則反饋一個Ack包。

第2步 該節點接收到鄰居節點的Ack包后，添加該鄰居節點通信的最低要求功率到節點鄰居信息表中。

第3步 當節點將發送功率遞增到最大發送功率后，對鄰居節點發送路徑預測信息分組(包括節點ID，到Sink節點的最短路徑權值預測值Di、節點剩余能量E(i))。鄰居節點收到這些信息后添加到鄰居信息表中。

第4步 節點根據當前剩余能量，執行相應的公式計算當前的發送功率Pi。節點采用發送功率Pi發送數據。

第5步 如果發送功率變換，更新相應的鏈路權值。節點根據鄰居信息表中信息，執行Bellman-Ford公式計算其最短路徑權值Dij。如果最短路徑權值發生變化，向鄰居節點發送路徑預測信息分組(包括節點ID，到Sink節點的最短路徑權值預測值Di、節點剩余能量E(i))。

第6步 根據鄰居節點的信息，節點選擇通信的最低發送功率小于當前發送功率且在最小權值路徑上的鄰居節點發送數據。

第7步 發送完若干比特數據后，跳到第4步，更新當前的發送功率。

經過上述步驟的循環，直到網絡死亡，即出現一個節點能量耗盡或數據不能到達Sink節點。在實現過程中，節點不時向其所有鄰居節點發送最新預測信息分組。鄰居節點獲得信息分組，更新鄰居信息表，執行Bellman-Ford公式，選擇最小路徑權值的節點發送數據。如果一段時間內，沒有接收到鄰居節點的最新預測信息分組或發送數據后沒有接收到反饋分組，則認為該鏈路出現故障，在鄰居信息表中刪去該鄰居信息。

節點i的偽代碼如下:

分析DPCRA_SPT算法的時間復雜性，假設節點發送預測信息分組的頻率是Hi。考慮最好的情況即所有鄰居節點Dj不變化，此時它的時間復雜度Θ(N(i))。考慮最壞的情況，即所有鄰居節點Dj都變化，每次變化都需要重新計算到Sink節點的最短路徑權值，此時它的時間復雜度是Θ(HiN(i))。

5 算法的仿真

5.1 仿真參數選擇

由于無線傳感網是應用相關的網絡，即不同的應用背景對無線傳感網的要求不同，所以研究者沒有統一網絡生存時間的度量方法。如果網絡中一個節點能量耗盡就會影響到網絡的正常運行，甚至導致網絡出現分裂，此時網絡生存時間的度量方法可定義為網絡開始運行到任意一個節點能量耗盡時的這一段時間，也可定義為網絡開始運行到網絡中任意一個節點數據不能達到Sink節點時的這一段時間［11］。它也可以定義為當某個網絡參數指標(如生存節點占總節點數量的比例、存活數據流占總數據流的比例、數據包到達率，或覆蓋度等)達到某一預先設定的閥值時，判斷網絡生存時間終止。但是對于不同的應用，甚至同一類應用的不同實例，網絡參數指標很難做出定量的判斷，過多地強調參數指標，反而使得網絡生存時間缺乏統一標準［12］。因此在仿真中，生存時間的度量值采用網絡開始到網絡中出現任意一個節點能量耗盡或節點數據不能達到Sink節點的這一段時間。

同時在仿真時，不考慮計算、數據融合、信息查詢分組收發等能耗，也不考慮數據傳輸過程中超時重發、出錯等能耗，只考慮數據無線通信能耗。選擇500 m×500 m網絡仿真區域，在該區域內隨機產生均勻分布的30、40、50、60、70、80、90、100 個無線傳感網節點(包括一個Sink節點)的位置分布，其中Sink節點固定坐標(250，250)。為了驗證算法的有效性，針對每個固定節點數量的無線傳感網，隨機產生10個不同的節點位置(即不同網絡拓撲結構)。根據表1的仿真參數分別計算這10個不同拓撲結構的無線傳感網生存時間、平均能耗和平均時延，最后取其平均值。

定義網絡生存時間的值為網絡開始運行到任意一個節點能量耗盡時Sink節點完成的數據收集周期個數DGC(Data Gathering Cycle)。一個DGC是指網絡中所有節點感知1 000g比特數據，并將數據發送給Sink節點所需要的時間。節點平均能耗=當一個節點能量耗盡時所有節點的總能耗/(節點數×DGC數)。節點平均時延=當一個節點能量耗盡時所有節點將數據發送給Sink節點的總跳數/(節點數×DGC數)。

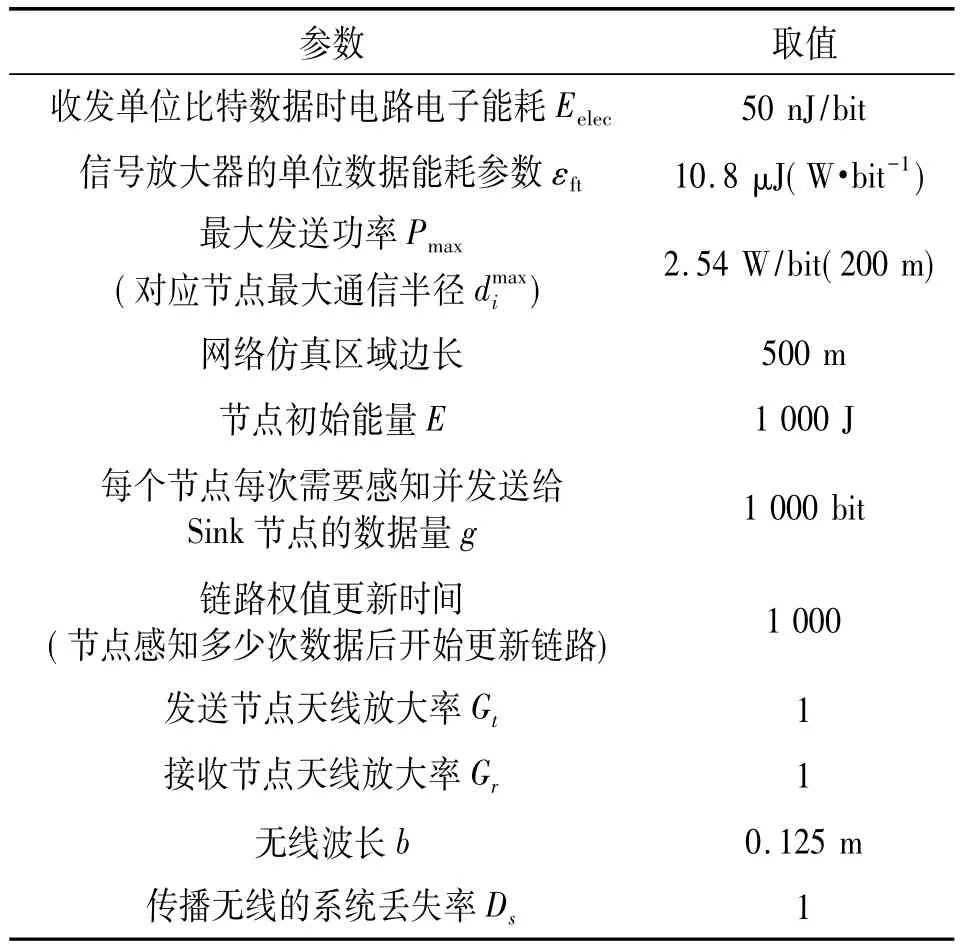
表1 仿真參數表

5.2 算法的關鍵參數研究

算法的關鍵參數是影響鏈路權值的α和β值，影響衰減模型的參數γl1，γl2，以下就是各個參數的選擇。

5.2.1 α 和 β值的選擇

研究式(7)中α和β值參數，在參數研究過程中采用窮舉法獲得仿真數據。選擇30、40、50、60、70、80、90、100個節點的無線傳感網，采用線性衰減模型，α 和 β 參數分別選擇{0.1，0.4，0.7，1，3，5}集合中的值，循環獲得所有可能的網絡生存時間和平均節點能耗。分析仿真數據可知:當DPCRA_SPT算法中的某個參數固定，另一參數可選擇{0.1，0.4，0.7，1，3，5}集合中的任意值進行仿真，仿真結果能顯示該參數的取值規律。為了方便說明，以其中一種典型數據為例分析參數取值規律，具體分析如下。

分析仿真數據可知(以 β=1，γl1=0.5，γl2=0.5為例，如圖3和圖4):在節點數給定后，當α≥1時，如果α偏向于5，網絡過多地考慮鏈路能耗在權值函數式(7)中的作用，著重考慮鏈路能耗，忽略了節點剩余能量參數，節點直接選擇鏈路能耗最小的路徑。由于此時容易產生樞紐節點導致能量消耗過快，因此網絡生存時間隨著α的增大而減小。當α≤1時，α 4種不同取值的網絡生存時間差別不大，但是從具體數據分析，當α=0.7時，網絡生存時間相對較大。雖然α≤1時網絡平均能耗變化不明顯，但是當α≥1時網絡平均能耗隨著α的增大而降低。這是因為當α≥1時，過多地忽略了節點剩余能量則導致當前發送路徑不理想，網絡生存時間下降明顯。由于計算平均能耗時需除以網絡生存時間，因此節點平均能耗也增加。

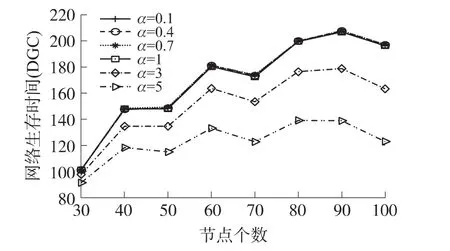
圖3 α因子對網絡生存時間的影響

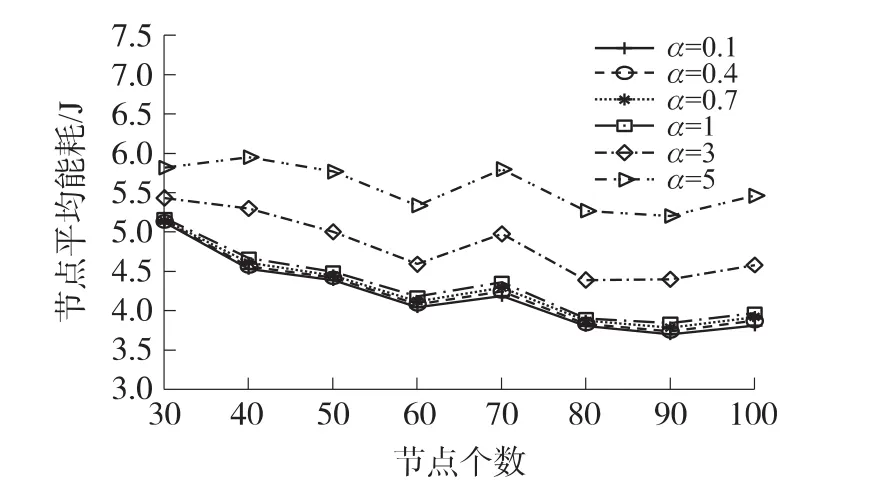
圖4 α因子對節點平均能耗的影響

總之，在DPCRA_SPT算法中，選擇適當的α可以延長網絡生存時間。

分析仿真數據可知(以 α=0.7，γl1=0.5，γl2=0.5為例，如圖5和圖6):當β≥1時，β≥3的網絡生存時間比β=1時略微增加。這是因為:在β≥3時，權值函數式(7)中鄰居節點剩余能量對權值函數的影響已經足夠大，這導致節點直接選擇剩余能量大的鄰居節點轉發數據，此時β值的變化基本不影響最短路徑選擇，從而使網絡生存時間相差很小。由于只是選擇剩余能量大的鄰居節點，基本上不考慮節點的鏈路能耗。當β≥1時，隨著β的數量增大，節點平均能耗增大。當β≤1時，在節點數給定后，β越接近于1，網絡生存時間越大。這是因為:β越小，權值函數過少地考慮節點剩余能量作用，權值函數偏向于鏈路能耗，因此網絡生存時間變小。由于幾個主干節點(即樞紐節點)轉發過多的數據，過早消耗能量而失效，但是其它節點能量消耗不大。因此當0.3≤β≤1時，網絡平均能耗相差不大。由于當β=0.1時，網絡生存時間下降太快，此時平均能耗偏大。

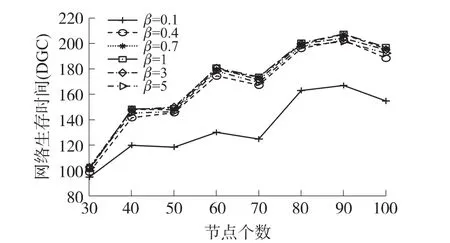
圖5 β因子對網絡生存時間的影響

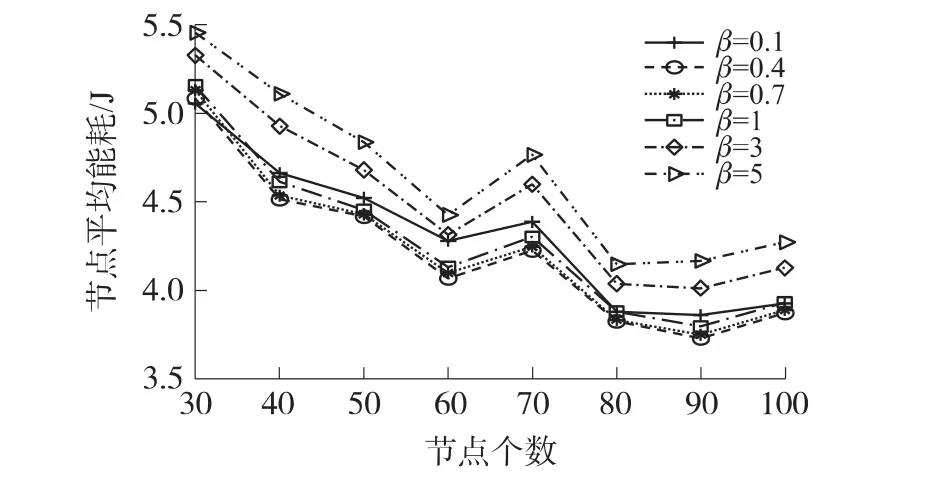
圖6 β因子對節點平均能耗的影響

總之，在DPCRA_SPT算法中，選擇適當的β可以延長網絡生存時間。

綜上所述，在DPCRA_SPT算法中，選擇適當的參數如α=0.7、β=1可以延長網絡生存時間、保持平均能耗在較低水平。

5.2.2 γl1和 γl2值的選擇

研究式(8)中γl1和γl2兩個參數，在參數研究過程中采用窮舉法來獲得仿真數據。在參數研究過程中選擇100節點的線性功率衰減模型，α=0.7，β=1，γl1和 γl2分別取值 0，0.1，0.2，…，1，二層循環得到網絡生存時間的仿真數據，獲得三維圖7。分析圖中網絡生存時間可知，當γl1固定值，剛開始網絡生存時間隨著γl2的增加而增加。當γl1和γl2兩個參數差不多時，網絡生存時間達到峰值，此后隨著γl2的增加而減少。

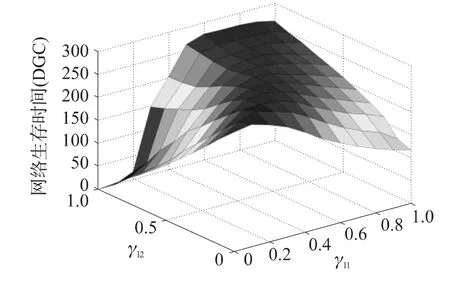
圖7 γl1和γl2對網絡生存時間的影響

總之，選擇適當的γl1和γl2值，DPCRA_SPT算法可以較好地反映網絡生存時間。

5.3 仿真結果和分析

根據5.2節的參數研究，得出能較好延長網絡生存時間的參數如 α=0.7，β=1，γl1=0.5 和 γl2=0.5，將DPCRA_SPT算法的鏈路權值公式改為:

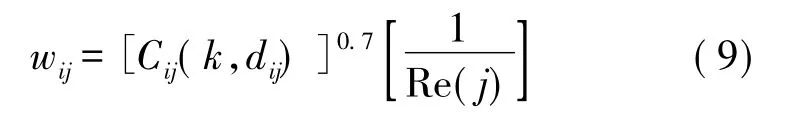
為了反映算法的有效性，選擇采用固定最大發送功率的Ratio_w算法(記為Ratio_w_FTP)，采用固定最大發送功率的 Bellman-Ford算法(記為BFFTP)，采用階梯衰減模型的Bellman-Ford算法(記為 BFSAM)［13］，采用 γn階二項式衰減模型的Bellman-Ford 算法(記為 BFPAM)［13］進行比較。

圖8比較了各算法的網絡生存時間。如圖可知:當節點數量是30時，由于網絡節點分布比較稀疏，一般節點通信需要最大發送功率，此時功率衰減模型反而降低了網絡生存時間，因此 BFSAM、BFPAM和DPCRA_SPT 3個算法的網絡生存時間比Ratio_w_FTP和BFFTP低，但是從數據上看BFFTP比Ratio_w_FTP略高。當節點數量大于30時，DPCRA_SPT的網絡生存時間最高，BFPAM次之，BFSAM第三，但這3個算法的網絡生存時間比Ratio_w_FTP和BFFTP高。這是因為當節點數量大于30時，隨著節點數量的增加，節點分布相對密集，此時節點不需要太大的發送功率，功率衰減模型體現出其價值，調整網絡的拓撲結構，從而延長網絡生存時間。節點分布越密集，延長網絡生存時間的效果越明顯。總之，當節點分布密集時，DPCRA_SPT算法，能延長網絡生存時間。

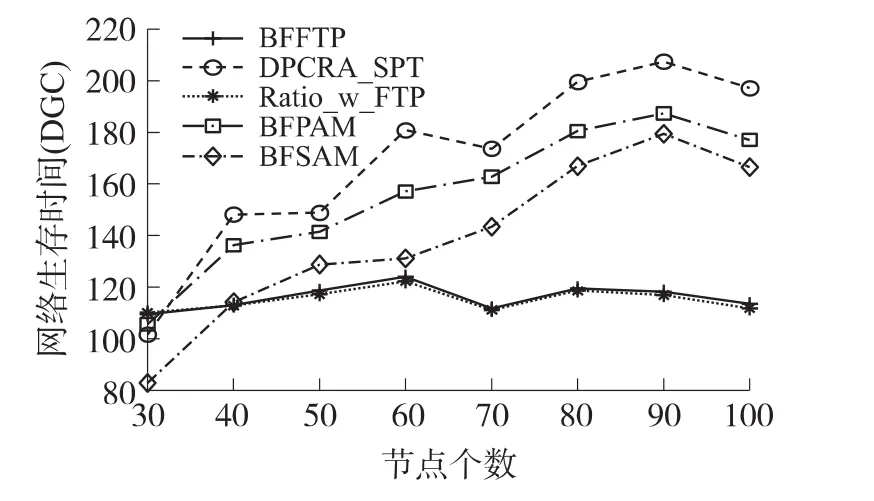
圖8 各算法的網絡生存時間比較圖

圖9比較了各算法的節點平均能耗。如圖可知:BFSAM的能耗最低，DPCRA_SPT算法次之，BFPAM算法第三，但是這3個算法都比Ratio_w_FTP和BFFTP算法低，而BFFTP算法和Ratio_w_FTP算法平均能耗基本一樣。這是因為:BFSAM、BFPAM和DPCRA_SPT這3個算法根據節點剩余能量的變化隨時改變自身的發送功率，調整網絡的拓撲結構，從而降低了節點的能耗。總之，DPCRA_SPT降低了節點的平均能耗，將能耗保持在較低的水平。

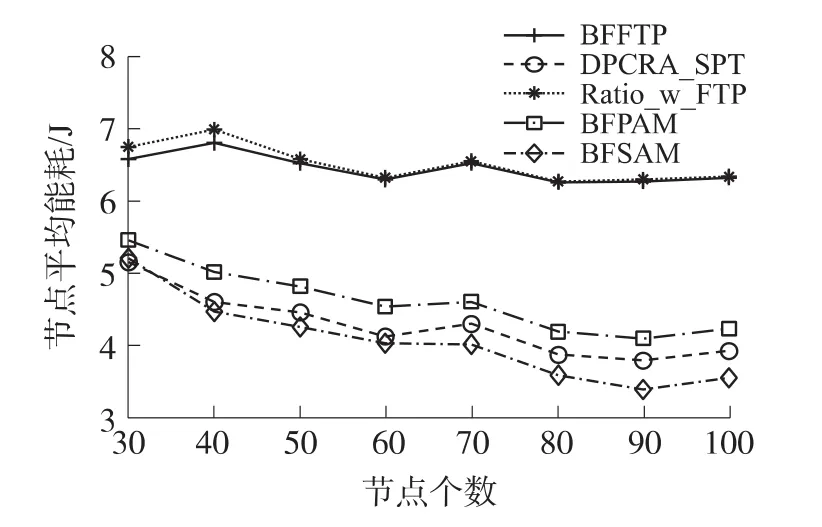
圖9 各算法的節點平均能耗比較圖

圖10比較了各個算法的節點平均時延(跳數)。如圖可知:BFSAM、BFPAM和DPCRA_SPT三個算法的網絡平均時延(跳數)波動很大，而且比BFFTP算法和Ratio_w_FTP算法高。這是因為，隨著節點剩余能量的減少，節點相對應減少了發送功率，可通信的范圍變小，此時數據到達Sink節點的跳數，即網絡平均時延增加。總之，BFSAM、BFPAM和DPCRA_SPT算法不能降低網絡平均時延(跳數)。

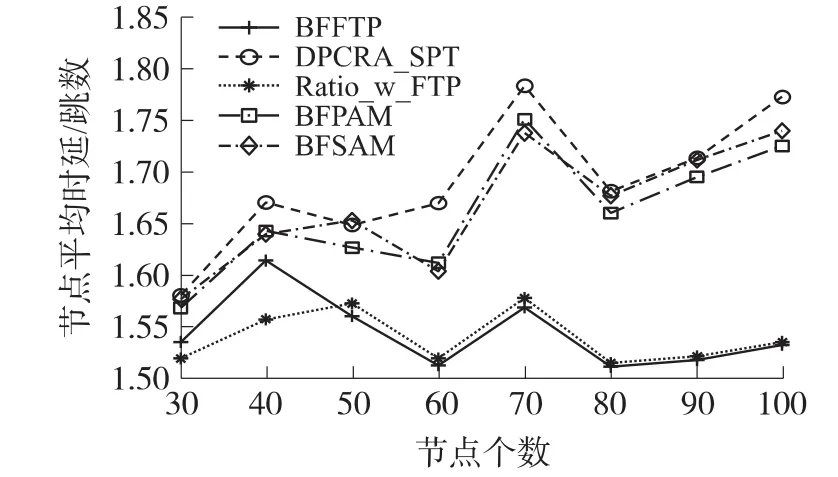
圖10 各算法的節點平均時延(跳數)比較圖

綜上所述，當節點分布密集時，DPCRA_SPT算法可以延長網絡生存時間，將能耗保持在較低的水平，比 Ratio_w_FTP、BFFTP、BFSAM、BFPAM 算法更優。

6 總結

如果節點不能測量到鄰居節點的距離，通過兩節點間距離調整發送功率就不可行，因此提出根據節點剩余能量改變自身發送功率的DPCRA_SPT算法。首先，詳細闡述鏈路能耗模型和系統假設。其次，考慮網絡中鏈路通信的能耗和鄰居節點的剩余能量，引入新的權值函數和功率線性衰減模型。運用分布式非同步Bellman-Ford算法構建最短路徑樹，所有節點沿著最短路徑樹將數據匯聚到Sink節點。最后，仿真分析權值函數式(7)和線性衰減模型中相關參數對網絡生存時間和平均能耗的影響，仿真比較DPCRA_SPT算法對網絡生存時間、平均能耗和平均時延的影響。

DPCRA_SPT算法適用于節點密集分布的無線傳感網，而且只是根據自身的剩余能量信息修改發送功率，當節點發送功率降低一定程度時容易造成網絡的分裂。因此下一步研究的工作是節點如何根據鄰居節點的信息，確定當前拓撲下的全局最優發送功率。

［1］朱藝華，楊晨曦，吳萬登，等.無線傳感器網絡權衡生存時間與數據分組跳數的分流路由算法［J］.傳感技術學報，2009，22(2):273－279.

［2］Manan R，Lall S.Distributed Algorithms for Maximum Lifetime Routing in Wireless Sensor Network［J］.IEEE Transactions on Wireless Communications，2006，5(8):2185－2193.

［3］He Y F，Lee I，Guan L.Distributed Algorithms for Network Lifetime Maximization in Wireless Visual Sensor Networks［J］.IEEE Transactions on Circuits and System for Video Technology，2009，19(5):704－718.

［4］Zhu Y H，Wu W D，Victor C M，et al.Energy-Efficient tree-Based Message Ferrying Routing Schemes for Wireless Sensor Networks［C］//Thirteen International Conference on Communications and Networking in China.Hangzhou，China，2008:25－28.

［5］朱藝華，沈丹丹，吳萬登，等.無線傳感器網絡優化生存時間的動態路由算法［J］.電子學報，2009，37(5):1041－1045.

［6］Fariborzi H，Moghavvemi M.EAMTR:Energy Aware Multi-Tree Routing for Wireless Sensor Networks［J］.Special Issue on Wireless Ad-Hoc Networks，2009，3(5):733－739.

［7］Wendi B H.Application-Specific Protocol Architectures for Wireless Networks［D］.Boston:Massachusetts Institute of Technology，2000.

［8］Gatzianas M A，Georgiadis L G.A Distributed Algorithm for Maximum Lifetime Routing in Sensor Networks with Mobile Sink［J］.IEEE Transactions on Wireless Communications，2007，7(3):984－994.

［9］Bertsekas D，Gallager R.數據網絡(第二版)［M］.盧剛，王康，譯.北京:人民郵電出版社，2004.

［10］Minhas R M，Gopalakrishnan S，Leung V C M.An Online Multipath Routing Algorithm for Maximizing Lifetime in Wireless Sensor Networks［C］//2009 Sixth International Conference on Information Technology.New Generations，2009:581－586.

［11］陳友榮，劉半藤，程菊花，等.無線傳感網優化生存時間的分布式功率控制［J］.傳感技術學報，2011，24(12):1787－1793.

［12］潘晏濤.傳感器網絡生存時間優化問題研究［D］.國防科學技術大學，2006.

［13］Chen Y R，Lu Y W，Cheng J H，et al.L.Distributed Power Control Algorithms for Wireless Sensor Networks［J］.Lecture Notes in E-lectrical Engineering，2011，98(2):319－326(EI).