基于峰值信噪比評價的運動模糊方向與長度識別

陳從平 汪 衛

（三峽大學 機械與材料學院，湖北 宜昌 443002）

在獲取一幅圖像時，由于成像系統與被拍攝對象之間存在著相對運動，引起所成圖像的運動模糊，其中勻速直線運動所造成的運動模糊最為常見，故具有一般性和普遍性.并且由于成像系統取得一幅圖像所用時間非常短暫，此時非勻速直線運動可以近似視為勻速直線運動［1］.勻速直線運動模糊圖像復原的關鍵主要在于運動模糊方向和長度的識別.根據運動模糊圖像和原始圖像在頻譜上存在的對應關系，常常使用Hough變換［2－3］或 Radon變換［4－6］檢測運動模糊圖像頻譜圖上暗條紋的方向和位置，然后根據模糊圖像的頻譜自動識別模糊方向和長度.雖然該方法較為簡單且成熟，但是識別的精度較低，據此識別結果的復原圖像效果也不理想.本文使用Hough變換對頻譜圖進行初次識別，然后以復原圖像與原模糊圖像的峰值信噪比作為評價標準對初次識別值進行偏差修正，識別結果精度非常高，根據識別結果對運動模糊圖像的復原效果較為理想.

1 算法原理

1.1 基于頻譜識別運動模糊方向和長度

根據成像系統的一般特性，線性和位置（空間）不變性，圖像的退化就是成像系統的退化加上額外的系統噪聲而形成的圖像的連續圖畫模型，可用下式描述：

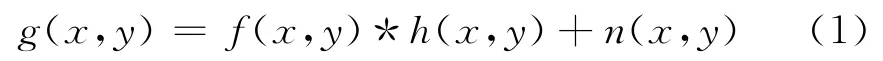
式中，g（x，y）表示所獲得的退化圖像（模糊圖像），h（x，y）表示成像退化的點擴展函數，f（x，y）表示原始圖像（清晰圖像），n（x，y）表示系統噪聲部分，根據經驗，這里設置成加性噪聲.

在直線運動中，可以將運動分解到x和y方向上，設x0（t）和y0（t）分別是景物運動在x和y方向的運動分量，T是曝光時間長度，在忽略加性噪聲的情況下，實際采集到的運動模糊圖像為

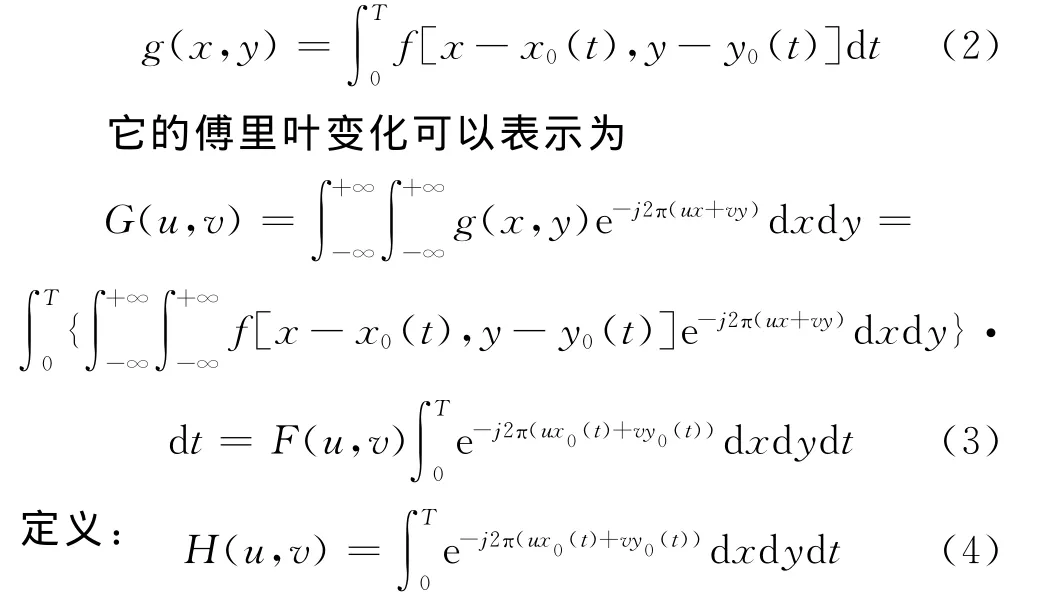
其中H（u，v）為運動模糊的傳輸函數.此時若知道了運動分量x0（t）和y0（t），從式（4）中可以求得傳遞函數h（x，y）的頻譜函數H（u，v），進而利用退化的逆過程對退化圖像進行復原［7－8］.

現在假設運動模糊長度和模糊方向分別為L和θ，在未知其實際值時通過頻譜分析對其進行自動識別，在識別模糊長度和方向之后對圖像進行復原.

對于任意角度的勻速直線運動模糊，都可以通過圖像旋轉，將模糊方向轉到水平方向上，此時y0（t）＝0，可以不考慮y方向分量的影響，x0（t）＝tL／T.

此時設置點擴展函數為

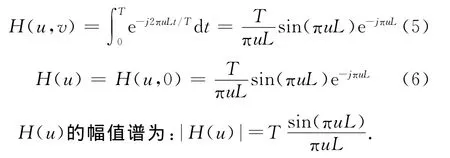
其曲線如圖1所示.在圖1中H（u）隨u與原點的距離增加而迅速減小.在實際獲取的圖像中，噪聲n（u，v）分布比較均勻，隨u的變化緩慢.如果H（u，v）在UV 平面內取零或很小時，N（u，v）／H（u，v）就會迅速增大，帶來嚴重的噪聲，使恢復結果與預期結果有很大差距，圖像退化更嚴重.在這種情況下，恢復只能在與原點較近（接近頻域中心）的范圍內進行.因此，在測定模糊方向與模糊長度時，取頻譜中心區域較暗的條紋進行參數計算，所得結果對恢復情況較為理想.

圖1 運動模糊的傳輸函數

運動模糊圖像和原始圖像在頻譜上存在一定的對應關系，模糊圖像頻譜存在對應于傳遞函數零點的暗條紋，通過算法檢測運動模糊圖像頻譜圖上暗條紋的方向與距離，可以實現運動方向與長度的識別.同時對中心暗條紋之間的距離測定得到模糊長度.

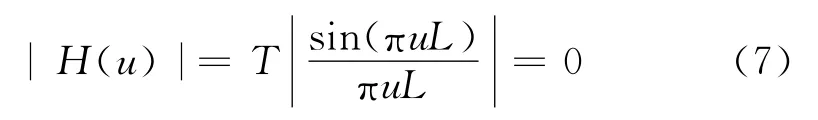
沿任意方向的直線運動模糊可以近似為沿x軸運動圖像的旋轉圖像.當n＝0時幅值H（u）取最大值，對應著頻譜圖中心亮條紋.當H（u）為零時u依次取±1／L，±2／L，±3／L…，分別對應著頻譜中的中心亮條紋兩側對稱的暗條紋.兩條暗條紋之間的像素距離就是d＝1／L，設所取圖像大小為N×M，則一個像素的長度為1／N，在曝光時間T內運動的像素個數為n，則L＝l／N.

通過對運動模糊圖像的頻譜圖分析其暗條紋的傾斜角可以得知模糊方向，有點擴展函數和線擴展函數傅里葉變換之間的關系可以證明，與x軸成θ夾角的直線的頻譜，其傅里葉變換等于在（u，v）平面內，與u軸成（θ＋90°）夾角的方向上的截面，對于與x軸成θ角的勻速直線運動，其頻譜一定在（θ＋90°）方向上存在暗條紋.

用霍夫變換（Hough）在模糊圖像中檢測暗條紋，取canny算子（敏感度閾值參數）thresh的初始值上限為經驗值0.85.

在極坐標中用如下參數方程表示一條直線：

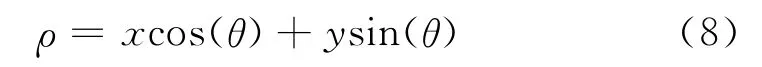
其中，ρ代表直線到原點的垂直距離，θ代表x軸到直線垂線的角度，取值范圍為±90°.與直角坐標類似，極坐標中Hough變換也將圖像坐標空間中的點變換到參數空間中，在極坐標表示下，圖像坐標空間中共線的點變換到參數空間中后，在參數空間都相交于一點，此時得到的ρ、θ即為所求直線的極坐標參數.

在由霍夫變換分割出兩條對應于模糊圖像中心暗條紋的平行直線后，通過取其平均值，可以減少分割時的誤差值.求得該直線的距離和角度參數，由此來反求運動模糊圖像的模糊角度與長度.

通過Hough變換求得d的值，故模糊像素長度和方向為

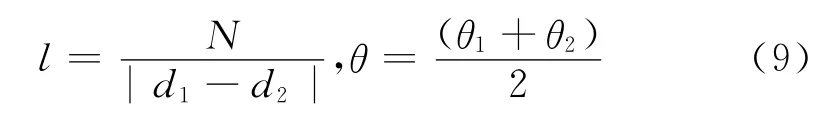
其中，d1，d2表示兩條暗條紋到圖像原點的距離（pixel），θ1，θ2表示兩條直線與x軸正向所成的角度（°）.

1.2 基于峰值信噪比對初次識別的模糊長度進行修正

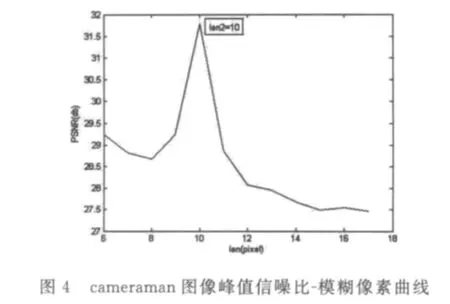
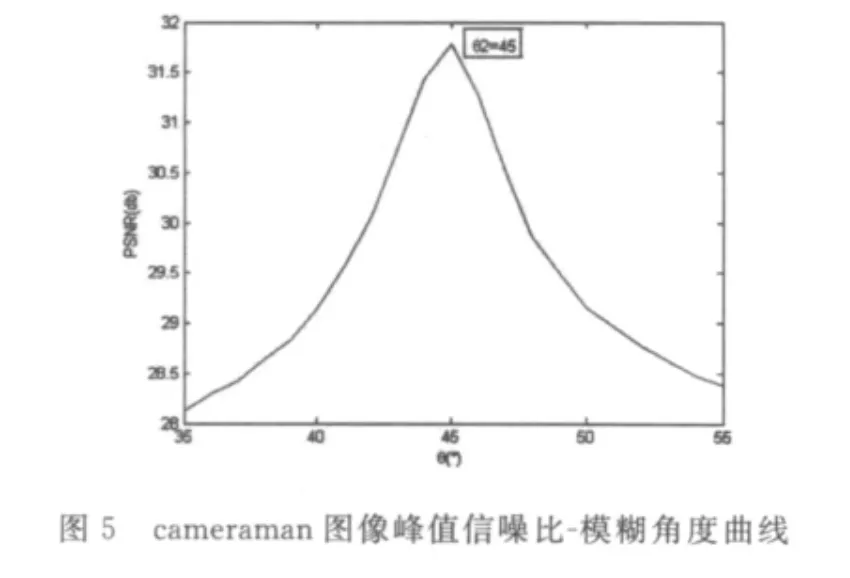
通過Hough變換分割出的平行線［9］檢測出圖像的模糊方向和模糊長度，由于分割中存在的不準確性，此時的運動方向和長度與真實值之間存在著一定的誤差［4］.根據上面檢查出的初方向和長度值利用維納濾波對模糊圖像進行復原，運動方向和長度與真實值之間的誤差導致點擴展函數與真實PSF也產生誤差，因而復原圖像的清晰度與真實圖像之間存在很大的差距，如文獻［3］中存在較大誤差.為了將圖像恢復到最接近原始清晰圖像，而對圖像的初次識別的方向與長度進行二次識別，當復原點擴展函數與模糊點擴展函數相一致時，復原圖像最清晰.由于從原始清晰圖像到復原圖像的兩次變換，基于真實的模糊長度時復原圖像的清晰度應該是最低的，同時復原圖像與模糊圖像的峰值信噪比（PSNR）最大.在初次識別的運動方向與運動角度領域范圍內，利用不同的模糊長度對模糊圖像進行復原，對應于真實模糊長度的復原圖像最清晰，它與模糊圖像存在著最大的峰值信噪比.取所有復原圖像中，清晰倒數極大值和峰值信噪比極大值圖像所對應的方向與長度作為最終識別的模糊方向與長度.

峰值信噪比：

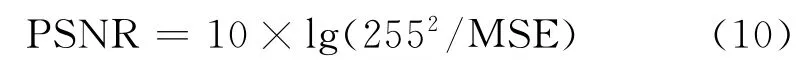
其中，MSE是原圖像與處理圖像之間均方誤差.m，n表示矩陣的行數與列數，PSNR的單位為dB.所以PSNR值越大，就代表失真越少.復原圖像與原始清晰圖像最接近，復原效果達到最佳.

取初次識別的模糊長度和模糊方向的領域內的一些列值建立點擴展函數對模糊圖像進行復原.得到相應的系列復原圖像，以檢測出的最大峰值信噪比復原圖像所對應的模糊長度和方向為真實值，從而對初次識別的模糊長度和方向進行了修正.其中最大峰值信噪比對應的復原圖像為清晰復原圖像.

2 識別算法流程

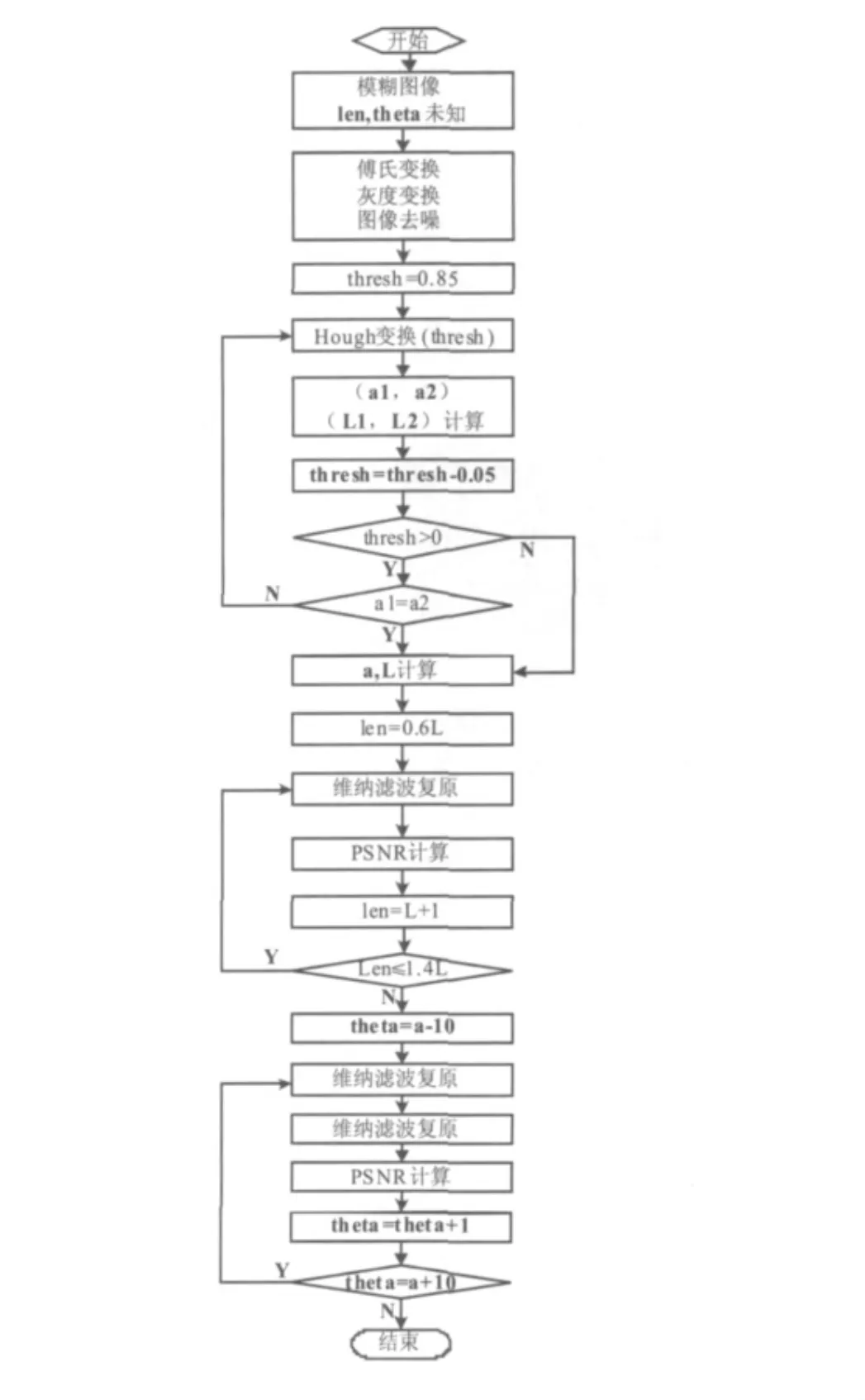
圖2 模糊方向和長度識別算法流程圖

在Matlab（2009）中對模糊圖像進行處理的過程為：將原始圖像進行任意角度和長度運動模糊，得到模糊圖像，對其進行預處理，主要包括傅氏變換，灰度變換，圖像去噪.然后對所得頻譜圖進行霍夫變換再進行直線檢測，得到基本重合于中心暗條紋的直線，根據直線的方向和間距計算模糊角度θ和長度L，其為初次識別值.然后在初次識別的基礎上根據峰值信噪比進行修正，以減少Hough變換產生的誤差.方法為：首先確定模糊方向θ，取初次識別的模糊長度為領域中心點，在一個較小領域［0.6L，1.4L］內對模糊圖像復原，求得復原圖像與模糊圖像的峰值信噪比，將最大峰值信噪比對應的長度確定為模糊長度修正值.然后，在上述識別的模糊長度L的基礎上，以初次識別的方向值為領域中心取一個小領域［θ－10，θ＋10］對模糊圖像進行復原，取復原圖像最大峰值信噪比對應角度為方向修正值.本文將以上方法得到的長度與方向修正值作為最終識別結果.

3 圖像處理過程

在Matlab（2009）中對多幅圖像經由前文所示算法流程進行仿真模擬實驗，得到一系列處理圖像.其中cameranman圖像識別過程圖如圖3所示.

圖3 運動模糊方向與長度識別與復原

圖3（a）為灰度圖像cameraman.tif的原始圖像，圖3（b）為圖3（a）直線勻速運動、方向為45°、模糊距離為10個像素的模糊圖像，圖3（c）為圖3（a）的頻譜圖，圖3（d）為圖3（b）的頻譜圖，圖3（e）為用 Hough變換分割圖像時的Hough矩陣和峰值點圖，圖3（f）為圖3（d）經過Hough變換分割出的對應于模糊圖像頻譜暗條紋的平行直線，圖3（g）是利用初次識別的運動參數進行維納濾波對模糊圖像圖3（b）的復原圖像，圖3（h）是利用修正后的模糊方向和長度的最終復原圖像.圖4為復原圖像關于模糊像素的峰值信噪比評價曲線，圖5為復原圖像關于模糊方向的峰值信噪比評價曲線.

對Cameraman.tif圖在Intel（R）Core（TM）2 2.33GHz四核 CPU，2.34GHz 2.0GB內存，Matlab2009a平臺下進行仿真，在長度為像素、方向為度的精度級下，基于頻域識別運動的模糊方向和模糊度［5］的識別方法耗時1.203 9s，本文方法耗時1.820 7 s，由于計算量的增加使時間增加了51.23%.由于算法的時間復雜度都在1～2s左右，相對于時間的少量增加，算法的識別結果的精度有明顯的提高.

4 實驗結果分析

通過以上算法進行仿真實驗，對cameraman.tif，lena.jpg兩幅圖像進行任意方向和長度的運動模糊，通過本文算法的模糊方向和長度的識別結果見表1和表2.

表1 cameraman圖像任意模糊方向和長度的自動識別結果

續表1 cameraman圖像任意模糊方向和長度的自動識別結果

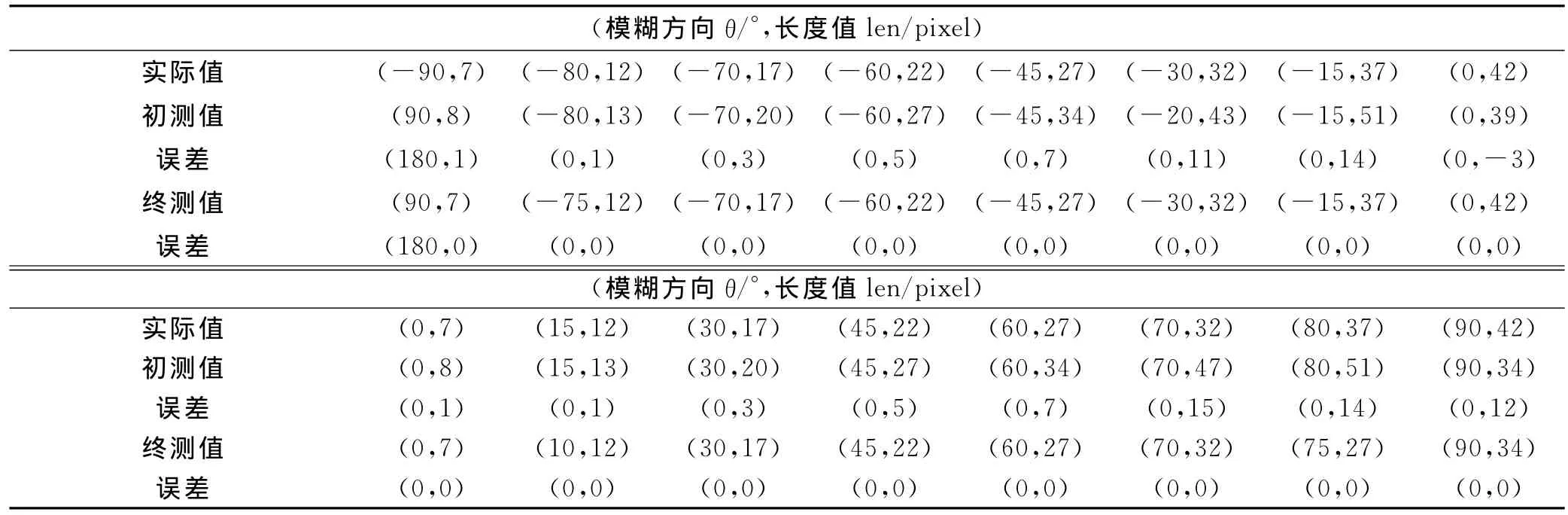
表2 lena圖像任意模糊方向和長度的自動識別結果

表1為cameraman圖像任意模糊方向和長度的自動識別結果，表2為lena圖像任意模糊方向和長度的自動識別結果.

首先通過頻譜暗條紋的分割直線檢測出運動模糊方向和角度.在初次識別存在誤差的情況下，基于復原圖像峰值信噪比對初次識別結果進行修正，能使誤差降到較小范圍，從而實現了運動模糊方向和長度的精確識別.通過本文方法識別的運動長度與方向均在誤差范圍之內，結果較為精確.在方向為－90°時，由于Hough變換是與90°方向共線，導致識別結果為90°，但是基于－90°與90°復原效果一致，對于－90°識別的結果可以認為是在誤差范圍之內.

將常用算法和本文算法取實拍模糊圖像進行復原效果對比分析.取在高速行駛的車中實拍的窗外模糊景像圖分別用基于頻譜Radon變換法［5］、神經網絡法［4］以及本文算法對其進行復原效果對比，結果如圖6所示.

圖6 運動模糊圖像的復原結果

圖6（a）為原始清晰圖像經過運動模糊所得的模糊圖像，圖6（b）為基于頻譜Radon變換法對于模糊圖像的復原圖像，圖6（c）為用神經網絡法的復原圖像，圖6（d）為本文算法的復原圖像.由以上3種方法對模糊圖像的復原效果可看出，用本文算法復原后的圖像清晰度比另外兩種算法復原后的圖像清晰度高.

表3為實拍模糊圖像的復原圖像與原始模糊圖像峰值信噪比（PSNR）對比結果，通過數據比較可以看出本文算法復原后圖像的PSNR比其它兩種算法高，評定為其復原效果優越，進一步驗證了本文算法的有效性.

表3 復原圖像峰值信噪比（PSNR）對比（單位：dB）

5 結 語

本文通過峰值信噪比曲線修正初始頻譜識別參數誤差，可以對任意方向和長度上的勻速直線運動模糊方向和長度進行精確識別.相較于文獻［3，5，10，11］所用方法在精度上有了明顯的提高.利用本文方法識別的模糊方向和長度與真實值誤差基本為零，算法原理簡單，準確率高.基于上述識別的模糊方向和長度所得復原圖像峰值信噪比高，復原效果較為理想.

［1］ 章毓晉.圖像工程［M］.1版.北京：清華大學出版社，2001.

［2］ 蔣巖峰，于起峰，梁永輝.基于頻譜分析的勻速運動模糊圖像模糊方向識別［J］.光學與光電技術，2008，6（4）：68－70.

［3］ 梁婉玉，孫權森，夏德深.利用頻譜特性鑒別運動模糊方向［J］.中國圖像圖形學報，2011，16（7）：1164－1169.

［4］ 萬 里，路林吉.基于頻譜參數估計和神經網絡的運動模糊圖像恢復［J］.計算機工程，2004，30（10）：132－134.

［5］ 梁 宇，鐘金榮，林嘉宇.基于頻域識別運動模糊的模糊方向和模糊度［J］.微處理機，2011（1）：59－63.

［6］ Mohserz Ebrahmi Mughaddam，Jamzad M.Finding point spread function of motion blur using radon transformand modeling the motion length［J］.IEEE，2004：314－317.

［7］ 賀衛國，黎紹發.勻速直線運動模糊長度的精確估計［J］.計算機應用，2001，21（9）：40－41.

［8］ 王曉紅，趙榮椿.勻速直線運動模糊的PSF之估計［J］.計算機應用，2001，21（9）：40－41.

［9］ 張 錚，王艷平，薛桂香.數字圖像處理與機器視覺［M］.1版.北京：人民郵電出版社，2012.

［10］郭永彩，郭瑞瑞，高 潮.運動模糊圖像點擴展函數的參數鑒別［J］.儀器儀表學報，2010，31（5）：1052－1057.

［11］陳從平，秦 武，王 健.基于清晰度評價的圖像運動模糊圖方向鑒別［J］.三峽大學學報：自然科學版，2010，32（2）：89－91.