數(shù)控機床伺服系統(tǒng)摩擦的非線性參數(shù)辨識研究*

陳光勝 李郝林

（上海理工大學機械工程學院，上海 200093）

伺服系統(tǒng)中的摩擦環(huán)節(jié)會使進給機構出現(xiàn)爬行、振蕩，過象限突起以及較大的穩(wěn)態(tài)誤差等［1－2］。為實現(xiàn)伺服系統(tǒng)的高精度控制，在得到慣量、阻尼和摩擦等動態(tài)參數(shù)基礎上對伺服系統(tǒng)進行精確建模是必要的。然而，僅利用設計參數(shù)通過解析法無法得到滿意的結果。系統(tǒng)辨識是得到諸如摩擦類動態(tài)參數(shù)的有效的手段［3］。另外，由于進給機構運動部件潤滑及磨損情況直接影響摩擦參數(shù)，因此對伺服系統(tǒng)的摩擦辨識也是實現(xiàn)機床性能評估和狀態(tài)監(jiān)測的需要。

盡管目前已有多個摩擦模型如:庫侖+粘性模型［5］、Stribeck 模型［6］、Karnopp 模型［7］、LuGre 模型［8］和GMS［9］模型等。但Stribeck摩擦模型仍然是目前較為公認的成熟模型，由于該模型能對摩擦的靜態(tài)特性能準確描述，因此在伺服系統(tǒng)的摩擦建模中被廣泛采用。本文將針對數(shù)控機床的伺服系統(tǒng)，對進給系統(tǒng)運動機構中存在的摩擦進行研究，通過非線性辨識則到精確的Stribeck摩擦模型參數(shù)。

1 摩擦的Stribeck模型

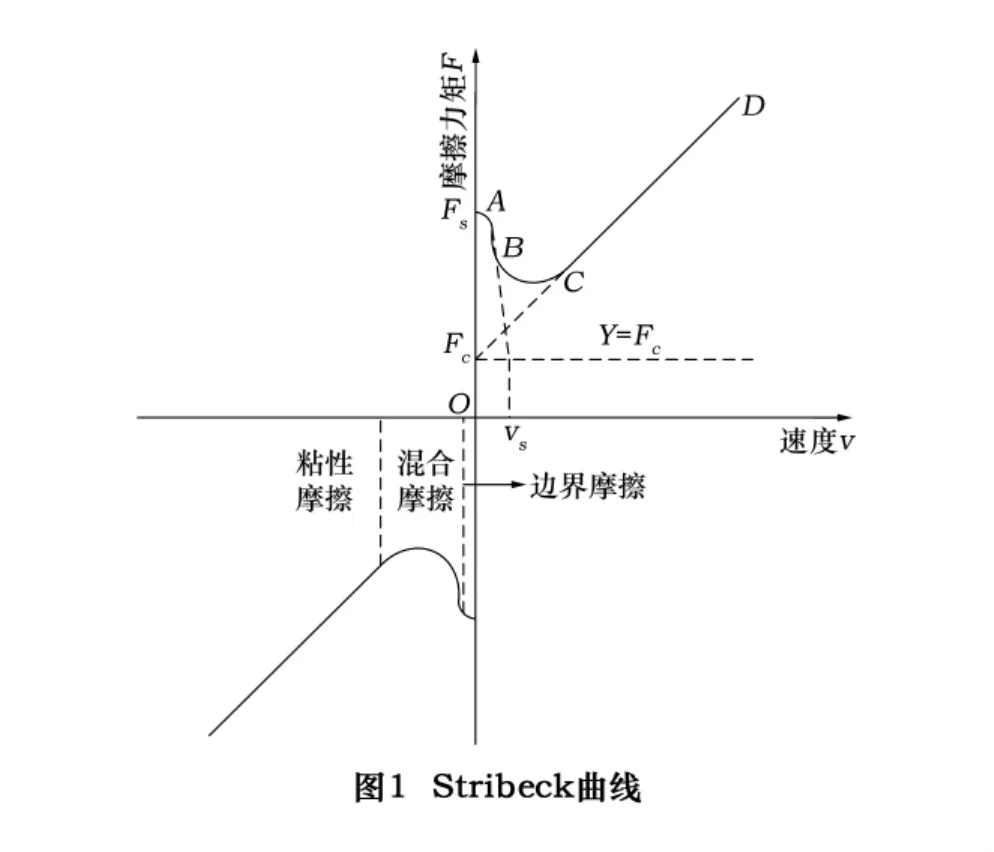
Stribeck模型也稱“指數(shù)模型”，該模型由Stribeck在1902年提出。他研究發(fā)現(xiàn)，兩物體間的摩擦力與相互接觸物體表面之間的潤滑油膜厚度有關，而接觸面之間的潤滑油膜厚度隨著相對運動速度的變化而發(fā)生改變，因此摩擦力表現(xiàn)為相對運動速度的函數(shù)。這就是人們所熟知的Stribeck曲線，如圖1所示。從Stribeck曲線可以看出，運動中的摩擦可以分為邊界摩擦、混合摩擦和粘性摩擦3個階段。在速度v較小時，隨著速度的增加，靜摩擦力逐漸以指數(shù)形式下降到庫侖摩擦;而隨速度v繼續(xù)增大，粘滯摩擦力與速度成線性關系。在穩(wěn)態(tài)運動時，摩擦力與速度的關系如下式:

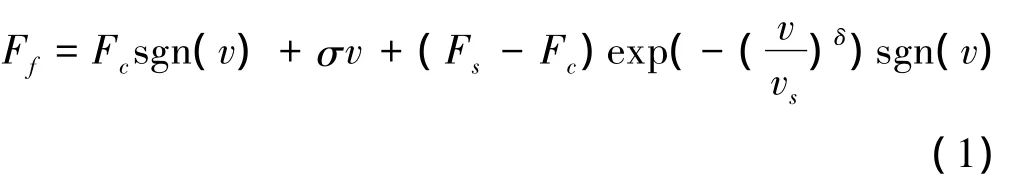
式中:Fc為庫侖摩擦力;Fs為靜摩擦力;σ為粘滯摩擦因數(shù);vs為臨界Stribeck速度;δ為Stribeck形狀系數(shù)，通常取1。Fc、Fs、σ和vs等參數(shù)需要通過參數(shù)辨識得到。

2 Stribeck模型參數(shù)非線性辨識

從式（1）可以看出，Stribeck模型為指數(shù)形式，因此無法利用線性的方法進行辨識，必須要實現(xiàn)非線性模型的線性化。

2.1 基本原理

將式（1）中指數(shù)項按泰勒公式展開，以6次為例，式（1）寫成:

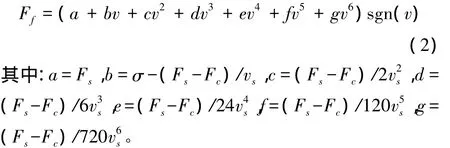
式（2）將摩擦力Ff寫成了速度v的各次冪的線性表達式。當通過實驗得到多組Ffi、vi序列時，令

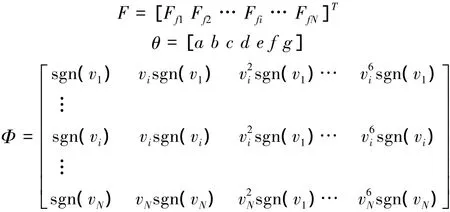
根據(jù)式（2），得

根據(jù)最小二乘法進行參數(shù)擬合，得到^θ，從而得到摩擦模型各參數(shù)

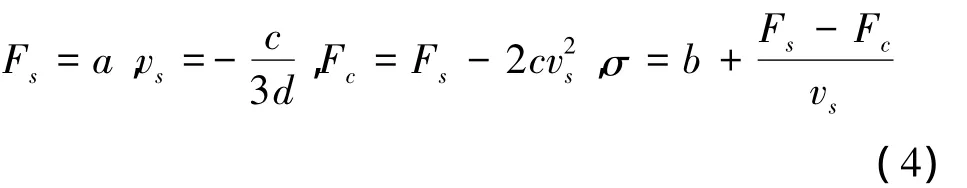
為了計算方便，在伺服電動機驅動的伺服系統(tǒng)中，摩擦力、速度也可以表示為Tf轉矩（N·m）和ω轉速（rad/s），這時，摩擦模型參數(shù)的單位也做相應調整。

2.2 實驗曲線的獲得

簡化的伺服系統(tǒng)控制模型如圖2所示，進給系統(tǒng)的移動部分和轉動部分質量、阻尼、摩擦力均等效到伺服電動機的轉動慣量Je、Be、Te

對于圖2所示的模型，有

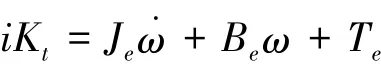
當機床工作臺沿導軌勻速進給且空載運行時，電動機勻速轉動，有˙ω=0，上式寫成

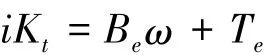
將阻尼力視為摩擦的一部分，這時

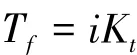
其中:Tf為機床在勻速進給時的摩擦力矩。

使機床伺服軸在不同速度下勻速空運轉，通過信號采集系統(tǒng)得到電動機的電流i和轉速n，即可得到電動機摩擦力矩Tf和轉速n關系，并可換算為工作臺進給速度v與摩擦力Ff的對應關系，并得到Stribeck曲線。

3 Stribeck模型參數(shù)非線性辨識實驗

伺服系統(tǒng)的Stribeck模型參數(shù)辨識實驗在某大型數(shù)控磨齒機砂輪修整系統(tǒng)進行，以對Y軸移動部件的摩擦為研究對象（圖3）。Y軸伺服電動機扭矩常數(shù)Kt=1.1N/A，絲杠導程L=5 mm。

Y軸在空載情況下，采用不同的進給速度勻速往復進給，分別采集正向和反向進給時的電流值i和進給速度F。由于方法相同，本文僅以正向進給時的摩擦來研究，得到對應的摩擦力矩Tf和角速度ω的對應如表1所示，繪制的角速度與摩擦矩的離散點如圖4所示。

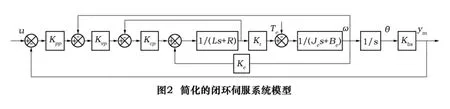
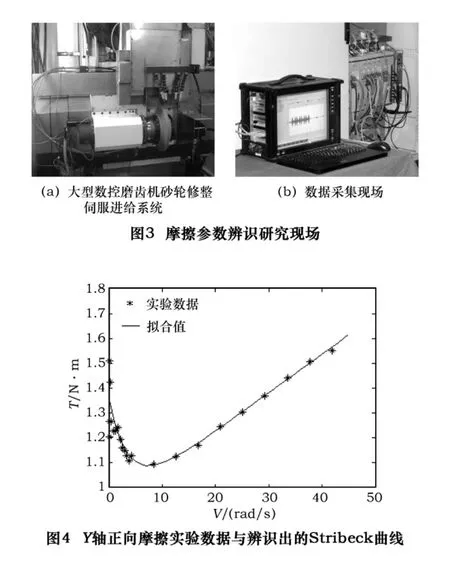
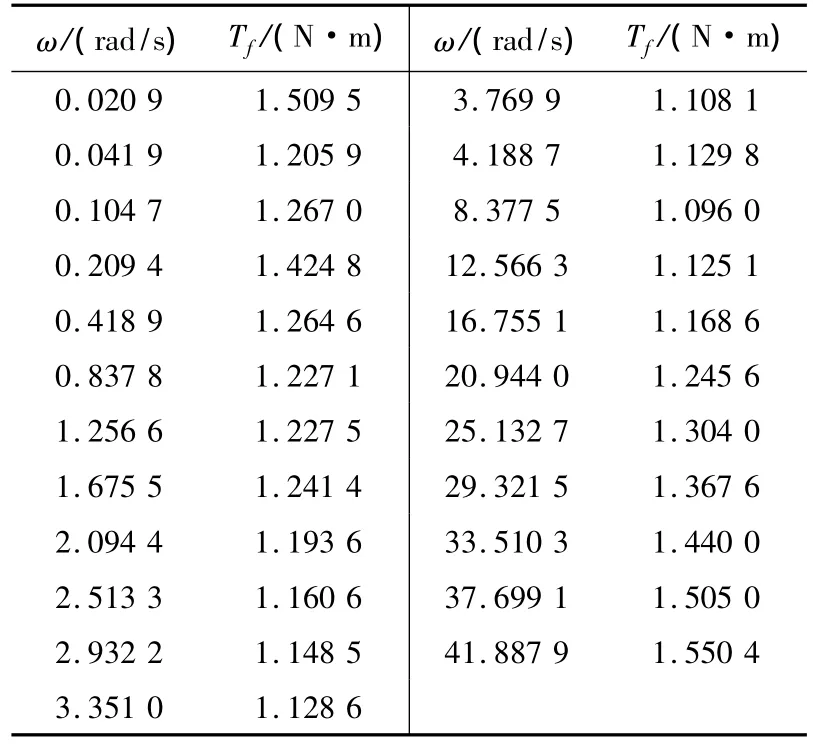
表1 Y軸伺服系統(tǒng)正向進給時的速度與電流

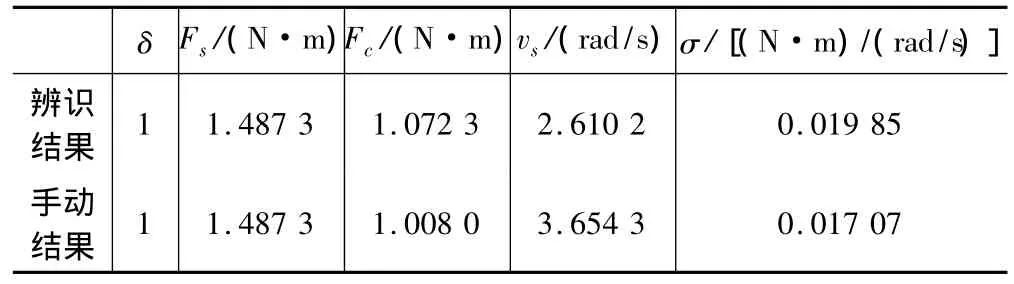
表2 Stribeck模型參數(shù)辨識結果

根據(jù)式（2）、（3），利用最小二乘法可以得到Stribeck摩擦模型的參數(shù)，在此基礎上進一步手工調整得到優(yōu)化的參數(shù)，利用優(yōu)化后的參數(shù)能很好地擬合實驗數(shù)據(jù)，如圖4（實線）所示。辨識結果如表2所示。

4 結語

針對非線性的摩擦指數(shù)模型，提出用泰勒高次展開的方法達到摩擦模型的線性化，通過最小二乘擬合的方法得到摩擦模型的參數(shù)。為驗證方法的有效性，針對數(shù)控機床進給系統(tǒng)移動部件進行了辨識實驗，實驗結果表明，該方法能對Stribeck摩擦模型的參數(shù)進行精確的辨識。該方法不僅適合于數(shù)控機床進給系統(tǒng)的靜態(tài)建模，而且可以用于進給系統(tǒng)潤滑或裝配性能的評估，在工程應用中具有實用價值。

［1］Mei XS，Tsutsumi M，Tao T，et al.Study on the compensation of error by stick－slip for high－precision table［J］，International Journal of Machine Tools＆ Manufacture，2004，44:503－510.

［2］劉強，爾聯(lián)潔，劉金琨，等.摩擦非線性環(huán)節(jié)的特性、建模與控制補償綜述［J］.系統(tǒng)工程與電子技術，2002，24（11）:45－59.

［3］Cohn S.Dynamic friction measurement，modeling，and compensation for precise motion control［D］.New Jersey:New Jersey Institute of Technology，1998.

［4］周玉清.基于無傳感器信息的數(shù)控機床伺服進給系統(tǒng)性能評估研究［D］.西安:西安交通大學，2009.

［5］Zhang H J，Landers R G.Precision motion control methodology for complex contours［J］.Journal of Manufacturing Science and Engineering，Transactions of the ASME，2007，129（6）:1060－1068.

［6］Siciliano B，et al.Experimental Robotics VIII［M］，STAR 5，2003:328－337.

［7］Karnopp D.Computer simulation of stick slip friction in mechanical dynamic systems［J］.ASME Journal of Dynamic Systems，Measurement and Control，1985，107:100－103.

［8］Canudas D W C.A new model for control of systems with friction［J］.IEEE Tran.on Automatic Control，1995 ，40（3），419－425.

［9］F Al－Bender，Lampaert V，Swevers J，et al.The generalized maxwellslip model:a novel model for friction simulation and compensation［J］.IEEE Transactions On Automatic Control，2005，50（11）:1883－1887.