基于永磁同步電動機中混沌運動狀態觀測器的同步控制*
楊曉輝 劉小平 柳和生 徐少平
(①南昌大學機電工程學院,江西南昌330031;②南昌大學信息工程學院,江西南昌 330031)
永磁同步電動機混沌控制是非線性科學中的一個熱門研究領域,1990年,美國物理學家Ott、Grebogi和Yorke[1]提出利用參數微擾法(簡稱 OGY方法)控制混沌。隨后混沌控制研究已經涌現了大量的混沌控制方法,常用的控制方法有強迫遷徙法[2]、自適應控制、延時反饋控制[3-4]等。
永磁同步電動機是一種典型的多變量、強耦合非線性系統,在某些參數及工作條件下會呈現混沌行為[5],主要表現為轉矩和轉速的間歇振蕩、系統不規則的電磁噪聲等。這些不規則運動嚴重影響著系統的穩定運行,如何對永磁同步電動機系統中的混沌行為進行控制已成為關注的焦點。首先對永磁同步電動機的數學模型進行了精確線性化,然后利用相應的技術將其控制到平衡點,然而此方法較為復雜,使得物理實現較為困難[7]。給出了一種基于Washout濾波技術的永磁同步電動機混沌控制方法,但這種方法的控制代價較大[8]。
本文基于永磁同步電機中混沌運動的同步狀態反饋控制,設計了一種具有最簡形式的同步狀態反饋控制器,實現了永磁同步電動機中的混沌同步控制。
1 永磁同步電動機數學模型及其數字仿真
id、iq、ω為系統狀態變量,分別表示d軸定子電流、q軸定子電流和轉子機械角速度ω,永磁同步電動機的數學模型可以寫為
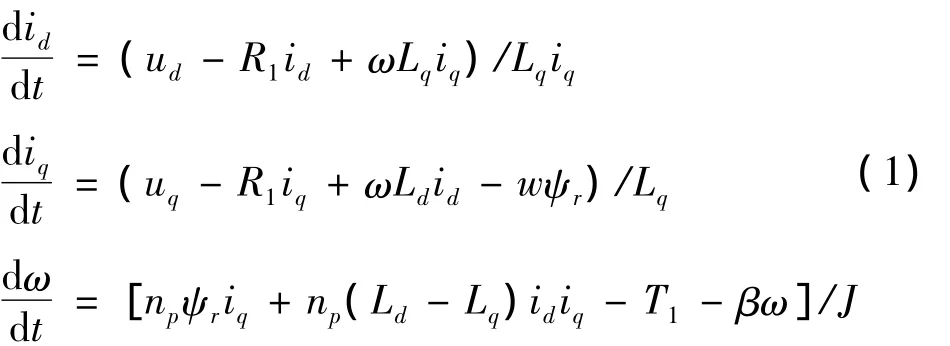
上述模型經過仿射和時間尺度變換后的均勻氣隙永磁同步電動機數學模型為

式中:id、iq、ω為系統狀態變量,分別表示d軸定子電流、q軸定子電流和轉子機械角速度;~ud、~uq和~TL分別為d、q軸定子電壓和負載扭矩;γ、σ為系統參數。
一般地,我們考慮電動機系統沒有外力的情形。這時可以看作是永磁同步電動機空載運行一段時間后突然斷電,各外部輸入項為零的情形,即~ud=0,~uq=0和~TL=0。此時式(2)系統可表述為
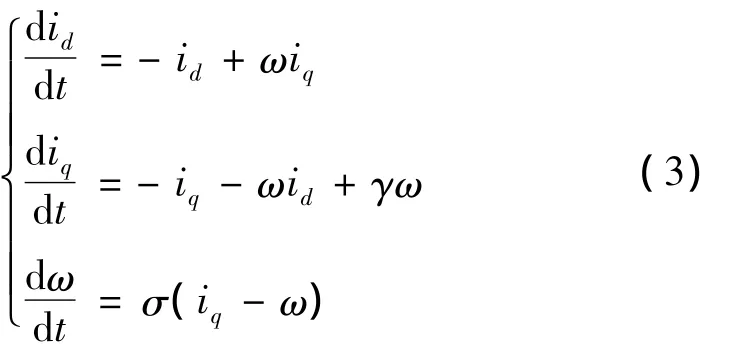
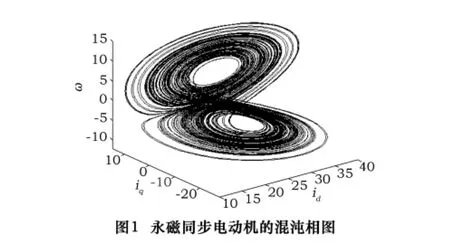
當 σ =5.45,γ 分別為16、20、100,式(3)系統存在不同的參數下呈現不同的動態行為。此時永磁同步電動機表現為混沌行為,其典型混沌吸引子如圖1所示。混沌的存在將嚴重破壞永磁同步電動機的穩定運行,甚至會引起傳動系統的崩潰。所以,必須抑制永磁同步電動機的混沌運動。
2 狀態觀測器法控制器的設計
式(3)系統可以被改寫為式(4)系統的第一行的形式為
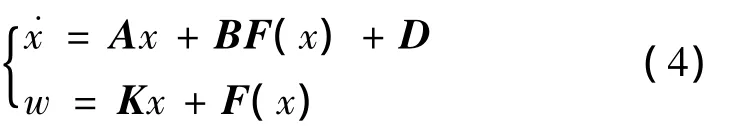
式中:x是系統狀態變量;A和B是已知的定常矩陣;D是系統的常數項;w是驅動系統的輸出;K是要求的反饋增益矩陣。比較式(3)與式(4),可得到系統參數為
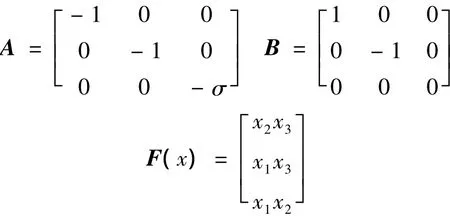
取

根據式(4)系統可設計其狀態觀測器為
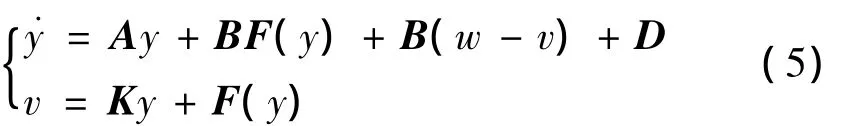
式中:y是狀態觀測器的狀態變量;v是狀態觀測器的輸出;D是系統的常數項。
定義式(4)和(5)系統的誤差矢量為

對式(6)求導,再將式(5)與式(4)代入,得到如下的動力學誤差系統為

令M=A-BK,則

如果對角矩陣K滿足條件λi≤0,其中λi是矩陣M的特征值,則式(7)的狀態向量漸近收斂到零,即式(4)驅動系統和式(5)響應系統漸近同步。通過解微分方程=Me,得
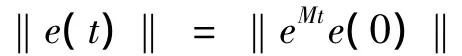
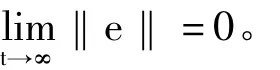
下面我們利用極點配置法來求增益矩陣K。式(1)系統不穩定平衡點為x0=[0.8,0.6,0.2],得到受控閉環系統在不穩定平衡點x0的Jacobi矩陣為
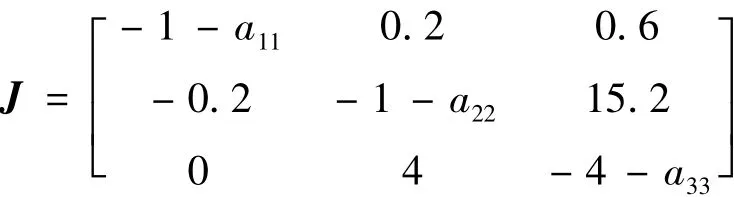
通過配置,可得到相應的K值。我們希望系統能夠滿足綜合指標為:輸出超調量σp≤5%;超調時間tp≤0.5 s,系統頻寬 ~ω≤10。,選其中一對主極點,另一個遠極點,可取希望的極點為s1,2= -7 ±3j,s3= -11,所以可以構成特征多項式,從而得到我們的a11、a22、a33,則可得到為
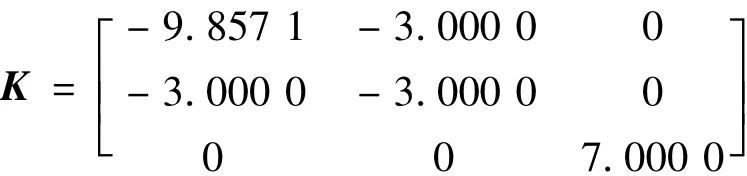
3 仿真結果分析
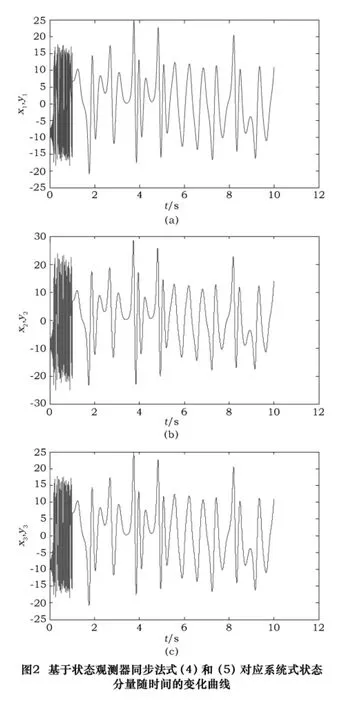
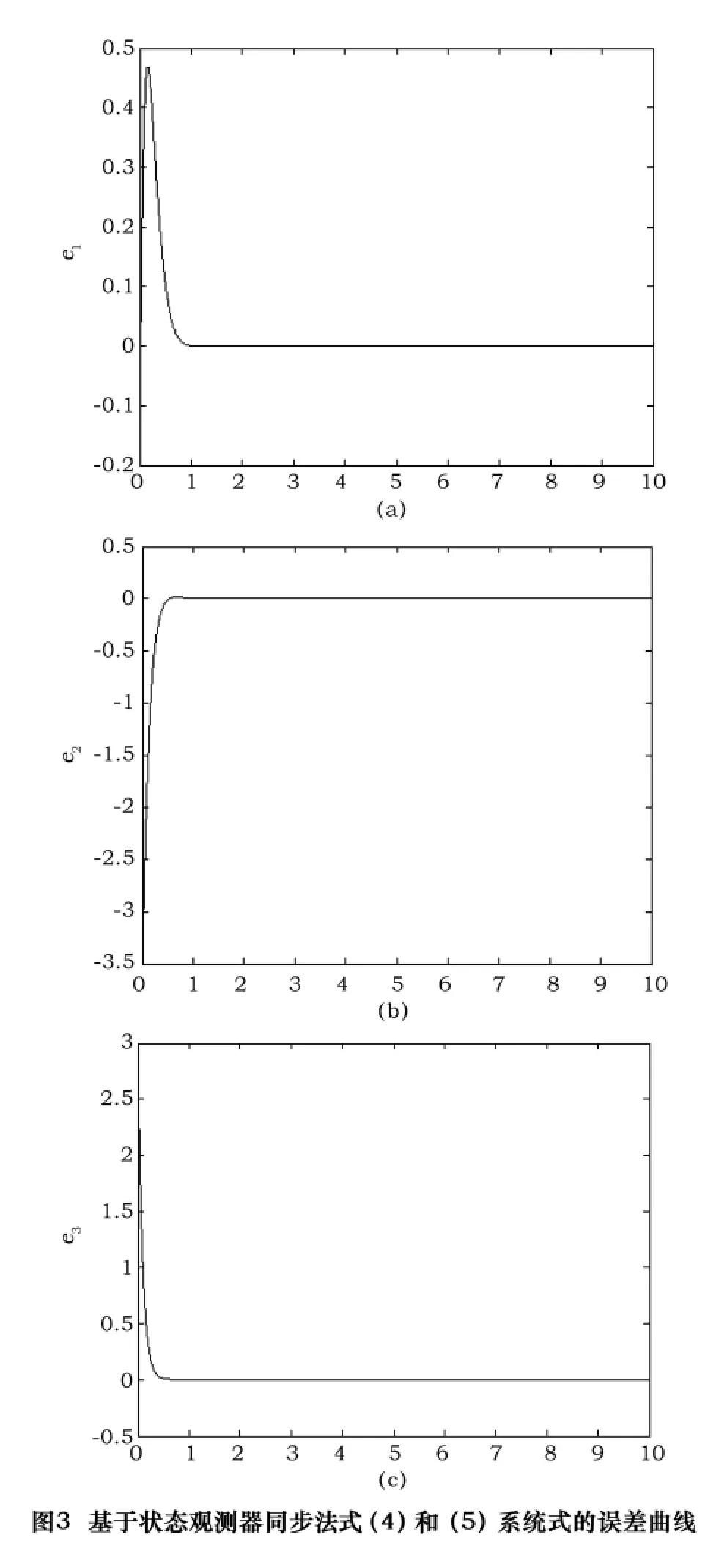
利用MATLAB軟件對以上得出的數據進行數值模擬,利用四階Runge-Kutta算法檢驗式(4)驅動系統與它的式(5)狀態觀測器是否達到同步。取步長為τ=0.001,式(4)驅動系統及其式(5)狀態觀測器的初始值為:x1(0)=0.8,x2(0)=0.6,x3(0)=0.2以及y1(0)=0.6,y2(0)=4.1,y3(0)=3.1;由誤差計算公式e=y-x可得初始誤差為:e1= -0.2,e2= -3.5,e3=2.9。圖2顯示了驅動-響應系統的對應狀態分量隨時間變化的曲線。圖3為誤差系統分量e1、e2和e3隨時間變化的曲線。從圖2和圖3可以看出,利用設計的增益矩陣K,很快實現了式(4)驅動系統和其狀態觀測器之間的同步。同時還可得出結論:對J取不同的值,通過極點配置法,可以得到多種增益矩陣K,即可設計多種狀態控制器,而且可以看到系統的動態響應特性完全符合期望的綜合指標要求。這說明基于狀態觀測器的同步法非常靈活,方便,具有很多優點。
4 結語
本文基于狀態觀測器的同步控制,實現了永磁同步電動機中的混沌控制。并且通過對極點配置來得到狀態觀測器進行同步控制,該控制器結構具有最簡形式,控制代價小,易于工程實現。另外,該控制器可以施加在狀態方程的任何一項上,所以控制方案實施起來很靈活。仿真結果表明了該方法的有效性,具有較高的應用價值。
[1]Ott E,Grebogi C,Yorke J A.Controlling chaos[J].Phys.Rev.Lett,1990,64:1196 -1199.
[2]李忠,張波,毛宗源,等.永磁同步電動機系統的納入軌道和強迫遷徒控制[J].控制理論與應用,2002,11(1):53 -56.
[3]李俊,陳基和,鄒國棠.永磁直流電機的混沌反饋控制[J].中國電機工程學報,2006,26(8):77 -81.
[4]張興華,王德明.無刷直流電機混沌系統狀態反饋控制仿真研究[J].微電機,2009,42(11),82 -85.
[5]張波,李忠,毛宗源,等.一類永磁同步電動機混沌模型與崔夫分叉[J].國電機工程學報,2001,21(9):13 -17.
[6]朱少平,錢富才,劉丁.不確定動態混沌系統的最優控制[J].物理學報,2010,59(4):2250 -2255.
[7]韋篤取,羅曉曙.基于LaSalle不變集定理自適應控制永磁同步電動機的混沌運動[J].物理學報,2009,58(9):6026 -6029.
[8]李春來.永磁同步電動機中基于沖洗濾波技術的混沌控制研究[J].物理學報,2009,58(12):8134 -8138.

