利用尋位信息的自由曲面在線測量路徑規劃方法*

邵 偉 郭俊杰

（①西安理工大學，陜西西安710048;②西安交通大學，陜西 西安 710049）

隨著航天、航空、造船、汽車等工業的飛速發展，使得自由曲面零件在現代工業中得到了越來越廣泛的應用，并且對產品性能、外形等方面的要求越來越高，而對該類工件的曲面建模、數控加工和產品表面質量評定都離不開對自由曲面工件幾何形狀的測量。其測量精度和效率直接影響到后續處理的質量和效率［1］。為了有效地實現對自由曲面工件的在線測量，就有必要對其進行合理的測量路徑規劃。測量路徑規劃是確定測頭在測量空間的運動軌跡，即工件上測量點的分布及其測量順序。測量時一般以面作為最小的測量單位，要求測量完一個面后，才能進行下一個面的測量。測量路徑規劃的好壞直接影響著測量效率和重構曲面的精度。測點數目的多少受到被測物體尺寸大小、檢測公差的精度要求和測量機測量精度大小的綜合影響。被測物尺寸大時，應進行多測點測量，尺寸小時則可進行少測點測量;測量的精度要求高時，測量的點數就應該多，反之則少;測量機的測量精度高時，測量相同物體的測點的數目可以少，精度低時就要多。在上述3項一定的情況下，就要對測量點的分布進行研究，使得測量點分布的疏密盡可能地隨曲面曲率的變化而變化，同時減小測量機自身誤差的影響，使測量結果盡可能地反映工件的實際形狀，從而在滿足精度要求的前提下使測點的數目盡可能的少，滿足在線測量高效率的要求［2－6］。

已知CAD模型的大型曲面測量規劃方法是在設計基準坐標系下根據加工精度要求確定測點數和測點分布，以及對應理論模型上的點，由這些點指導測量機進行測量，然后對加工機床進行相應的工藝指導，這就涉及到設計坐標系、測量坐標系、加工坐標的統一，因此在測量路徑規劃中如何實現設計坐標系、測量坐標系、加工坐標的統一對測量軌跡和加工軌跡的控制至關重要［7－8］。本文提出了一種基于工件尋位的方法，建立坐標系之間的相互關系實現坐標系的統一，其原理就是通過對工件上的特征點的測量來找出測量坐標系相對設計坐標系和加工坐標的相對位置關系，保證測量過程中測頭的運動與工件的CAD模型規劃軌跡一致。因此本文采用一種基于曲面工件自動尋位的坐標系統一原則和測點布置于一體的測量路徑規劃方法。下面首先介紹基于曲面工件自動尋位信息的坐標系關系的建立。

1 基于自動尋位信息的坐標系關系的建立

坐標系關系的建立就是要確定設計坐標系、測量坐標系、加工坐標系的相互轉換關系，即轉換矩陣的求解，因此，建立曲面測量坐標系與設計坐標系和加工坐標系之間的變換關系成為轉換矩陣的求解。針對CAD模型己知的待測大型曲面工件，可根據預先測量獲取的工件表面上少數測點的信息，通過一定的計算將其與CAD模型上對應的點對齊，快速準確地求解出工件的實際狀態（工件在測量機上的位置與姿態），即求解出測量坐標系和設計坐標系之間的真實關系。一般工件測量坐標系和設計坐標系之間的關系可用齊次變換矩陣T表示為

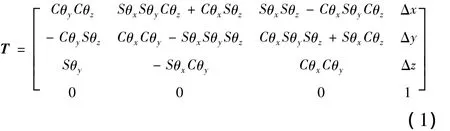
式中:Δx、Δy、Δz為測量坐標系原點相對于設計坐標系原點的平移量;θx、θy、θz分別為測量坐標系繞設計坐標系x、y、z軸的旋轉角度;S和C分別是sin和cos的縮寫。

由于直接快速精確求解T是比較困難的，為此本文采用如下的方法［9－10］來對模型已知的待測大型工件進行尋位信息提取。該方法具體步驟可描述如下:

（1）初始化——使變換矩陣T0為

其中（xc，yc，zc）為初始測點的質心;并且初始化與測點（i=l，2，…，n;j=1，2，…，m）對應的曲面上的理論點（i=l，2，…，n;j=1，2，…，m）。

（2）計算測點Pij與工件理論曲面間的偏差

（3）置k=k+l;

（4）確定測點Pij對應的曲面上的理論點

由于測量坐標系的測點相對工件理論曲面間距離的平方為

解方程組（5）求出所對應的參變量u、v的取值，最后將u、v之值代入坐標函數表達式，即可求出的坐標值;

（1）進行變換矩陣T更新得到Tk;

（2）求取變換后的測點:

（3）計算與工件理論曲面間的偏差

2 基于尋位信息的測量路徑規劃算法

實現曲面工件尋位測量的關鍵，是按所獲得的工件尋位信息對測量過程進行位姿自適應控制。下面提出一種對已知曲面進行測量的基于尋位信息的路徑軌劃方法。下面介紹算法的具體實現過程。

2.1 曲面工件的測點生成算法

如果對待測曲面工件的整個幾何形狀自適應地進行測點布置，將使得計算的工作量相當大，在一定的精度條件下也完全沒必要。一種合理的解決辦法就是首先根據給定的精度要求，在曲面上自適應生成檢測方向上的測量曲線，在避免漏檢的前提下盡可能減少測量曲線的數目;然后對每一條測量曲線按等步距進行測點布置以生成曲面工件的測點。其中曲面工件的測量曲線自適應生成就是根據待測曲面的具體幾何形狀自適應地進行測量曲線的布置，使測量曲線分布的疏密隨曲面曲率變化而變化，從而在滿足精度要求的前提下使測量曲線的數目盡可能地少，以提高測量的效率。如圖1所示，對應于一定精度要求的測量曲線生成過程如下:

步驟1:檢測方向上測量曲線的分布。對于曲面:

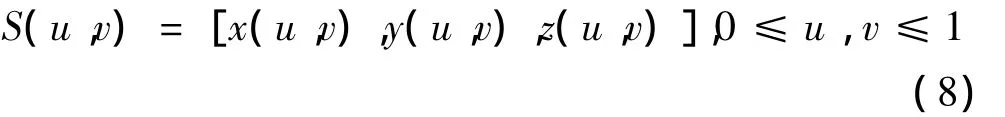
假設參數u方向（或v方向）為其檢測方向，并且沿該方向分布n條測量曲線，首先根據掃描間距用等參數方法進行曲面離散（如圖1所示），得到各離散型值點Sij=S（ui，vj）（i=l，2，…，r;j=1，2，…，l）。接著，將該離散的曲面按u方向（或v方向）劃分成m個離散小曲面，m一般應等于1/5～1/2倍的測量曲線數n。

接著，對每個離散小曲面中各點進行曲率數值的計算。根據歐拉公式，設{e1，e2}是曲面在任一P點的兩個彼此正交的主方向單位向量，對應的主曲率為k1、k2，則在P點沿任意一個單位切向量e=e1cosθ+e2sinθ的法曲率為

從式（9）不難看出，主方向正是法曲率取極值的方向，而主曲率正好是法曲率極值，即如果k1≥k2，則在曲面上在該點沿任意一個切方向的法曲率滿足不等式

在實際應用中，取曲面上P點的絕對曲率

反映曲面上該點的彎曲程度。其中，主曲率k1、k2分別為曲面在一點處的最小、最大曲率。進而通過式（11）可計算出各離散小曲面上各點的曲率測度及其最大最小值。

然后，對每個小曲面采用均勻分布的方法進行測量曲線的分布，分布曲線數ni為

到此，就完成了沿曲面u參數方向（或v方向）n條測量曲線的分布，并將這n條測量曲線作為當前測量曲線集C（n）。

步驟2:由上面確定的n條測量曲線重構CAD模型得到一個替代曲面模型S*。

步驟3:計算曲面模型S*與CAD模型之間的偏差Δ。設ε為測量精度和工序能力共同確定的精度要求，如果

不成立，并且n＜N（N為預先指定的正數），則令n=n+1，重復上述過程直至式（13）成立。于是可取C=C（n），由該方法所生成的測量曲線集可以滿足對曲面檢測測量曲線數目和自適應分布的要求，以便對曲面的形狀誤差做出準確評定。

2.2 幾何信息變換和測量路徑的生成

為實現對模型已知的大型曲面工件進行測量，需將待測曲面工件的有關幾何信息從設計坐標系變換到測量坐標系。因此，在求得齊次變換矩陣T后，可用T－1對由曲面CAD模型生成的測點數據Qij進行變換，即將CAD模型面的測點變換到測量坐標系中，其表達式為

遍歷上述測點數據即可得到的曲面測量路徑。

3 仿真與實驗

為了驗證上述算法的有效性，進行了多次仿真實驗。仿真實驗之一所用工件的CAD曲面輪廓如圖2所示。在一定的精度要求下，利用測量曲線自適應布置算法進行測量曲線自適應分布的結果如圖3所示。由圖中不難發現測量曲線的分布在曲面曲率大的地方分布得密，而曲率小的地方分布得疏。

對于該工件如按常規方法進行測量，則由于定位不準，使得工件的實際測點與理論測點產生較大的誤差，此時測量坐標系相對于設計坐標系的位移和旋轉量如表1第二列所示。為消除這種誤差，采用尋位控制方法對測量過程進行控制。為此先在工件表面上確定一定數量的測量點（本次實驗為10個），并取得這些點的坐標值，將這些測點的數據輸入控制計算機，運行該機中的工件定位控制軟件，經計算出被定位工件的狀態估計值即尋位計算值如表1最后一列所示。

用所求得齊次變換矩陣T后，將工件曲面的自適應測點從設計坐標系變換到測量坐標系，使設計坐標系和測量坐標系趨于一致，此時最大誤差為0.008 5 mm。這說明該尋位測量方法具有較高的精度，可以滿足曲面工件的測量要求。

表1 工件狀態

圖4為以自適應采樣路徑規劃得到的最小測量曲線行間距（5.236 1 mm）進行等行距測量曲線布置的結果，共有19條測量曲線。由此可見，和本文采用的測量路徑規劃方法相比，在相同的測量效果下，本文采用的測量路徑規劃得到的測量曲線數顯著減少，可以較好地提高采樣效率。

圖5為以自適應采樣路徑規劃得到的某工件測量曲線布置的結果和實際測量曲面的誤差分布圖，其結果和實際基本相符。由此可見，本文采用的測量路徑規劃方法在相同的測量效果下，可以較好地提高采樣效率。

4 結語

提出了一種基于尋位信息的大型曲面工件的設計坐標系、測量坐標系、加工坐標的統一方法，在此基礎上實現測量路徑規劃，實現測量過程中對測點的布置。該方法根據待測曲面上相鄰子曲面內測點的平均曲率為判據來進行測量曲線的自適應分布，可以保證測量曲線分布的疏密隨曲面曲率變化而變化，以提高測量的效率;接著對每一條測量曲線按等步距進行測點布置以生成曲面工件的測點。然后基于尋位信息，將測點從設計坐標系變換到測量坐標系。仿正和實例表明，上述方法具有算法簡潔、采樣精度容易控制的特點，在相同采樣精度下可顯著提高在線測量效率，滿足在線測量高效率的要求，有效提高加工質量。

［1］裘祖榮，石照耀，李巖.精密測試技術展望［J］.中國機械工程，2010，46（14）:1－11.

［2］靳宣強，姜秀麗，胡禎，等.淺析數控機床在線檢測技術［J］.現代制造技術與裝備，2009（3）:40－42.

［3］Seokbae S，Seungman K，Kwan H L.Path planning of multi－patched freeform surfaces for laser scaning［J］.Int.J.Adv.Manuf.Technol.，vol.224，pp.424 －435，2003.

［4］趙吉賓，劉偉軍，孫玉文，等.自由曲面測量點云數據的建模方法研究［J］.儀器儀表學報，2006，27（19）:1044 －1047.

［5］劉強，李冬茹.國產數控機床及其關鍵技術發展及展望［J］.航空制造技術，2010（10）:26－30.

［6］趙振宇，張萌，周后明.最短路優化的復雜型腔刀具軌跡規劃算法［J］.制造技術與機床，2009（1）:39 －42.

［7］石為人，王楷.基于Floyd算法的移動機器人最短路徑規劃研究［J］.儀器儀表學報，2009，30（10）:2088 －2092.

［8］梁義，陳建軍，陳立崗，等.幾何自適應參數曲面網格生成［J］.計算機輔助設計與圖形學學報，2010，22（2）:327－335.

［9］紀小剛，龔光榮.三坐標測量機中基于遺傳算法的多特征測量路徑規劃研究［J］.兵工學報，2005，26（3）:392 －396.

［10］徐金亭，孫玉文，劉偉軍.復雜曲面加工檢測中的精確定位方法［J］.中國機械工程，2007，43（6）:175 －179.