模糊自適應PI控制在直流無刷電動機調速系統的應用*
胡發煥 唐 軍 邱小童
(①江西理工大學機電工程學院,江西贛州341000;②江西理工大學應用科學學院,江西贛州 341000)
目前直流無刷電動機(BLDCM)廣泛應用于航空航天、軍事、工業、醫療機械等諸多領域。BLDCM是一個多變量、強耦合、非線性、時變的復雜系統[1],當系統負載或參數發生變化時,傳統的PID控制將難以達到設計的預期效果。對這類高度非線性的系統,采用智能控制方法可獲得更理想的效果,它具有提高系統的響應速度、穩定性和魯棒性的能力。模糊控制是智能控制中最常用的方法之一,它不依賴于控制系統的精確數學模型,且對系統參數的變化不敏感,具有快速性及魯棒性強的特點,適合BLDCM控制系統的要求。本文即采用應模糊自適PI控制的模式實現對BLDCM的控制。
1 工作原理及數學模型
直流無刷電動機主要由電動機本體和轉子位置傳感器兩部分組成。在電動機本體上安裝1臺同步電動機,轉軸上裝有轉子位置監測器,以測量轉子磁極與旋轉磁場的相對位置,為驅動電路提供參照信號。無刷電動機為了實現無刷換相,把直流電動機的電樞繞組放在定子上,把永磁鋼放在轉子上,這與傳統直流永磁電動機的結構正好相反。由位置傳感器、邏輯控制電路及功率開關電路共同組成換相裝置,使直流無刷電動機在運行過程中,由定子繞組所產生的磁場與轉子自身的永久磁場在空間始終保持約120°的電角度,從而產生磁轉矩推動轉子旋轉。現以二相導通星形三相六狀態無刷電動機為例,分析無刷直流電動機的數學模型[2]。三相繞組的電壓平衡方程為:

式中:ua,ub,uc為定子相繞組電壓;ia,ib,ic為定子相繞組電流;ea,eb,ec為定子相繞組電動勢;L為各相繞組的自感量;M為兩繞組間的互感量;P為微分算子d/dt。因電動機為星形連接且無中線,則有:

定子繞組產生的電磁轉矩方程為

則電動機的驅動方程為

其中:Te為電磁轉矩;TL為負載轉矩;B為阻尼系數;ω電動機的角速度;J電動機轉動慣量。
2 模糊自適應PI控制系統的設計
在電動機調速系統中,使用傳統的PID控制器,可以得到較好的動態性能。但電動機是主要的諧波源之一,在運行時會產生大量的電磁干擾,引入微分環節在改善控制器動態性能的同時,也會對噪聲信號進行放大,所以不合適的微分系數會使控制系統的穩態性能變差[3],通常使用 PI控制器就能滿足系統的性能要求,鑒于這個原因,本文設計的速度控制器不引入微分,而采用PI控制器。BLDCM是一個多變量、強耦合、非線性的復雜系統,當系統負載或參數發生變化時,要達到滿意的控制效果則必須實時改變PI控制參數,因此,傳統的PI控制器將難以達到滿意的效果。對這類高度非線性的系統,采用智能控制方法則可獲得理想的效果,它具有提高系統響應速度、穩定性和魯棒性的能力。模糊控制是智能控制中常用的方法之一,它具有不依賴于控制系統的精確數學模型,對系統參數的變化不敏感,具有快速性及魯棒性強的特點,很適合BLDCM控制系統的要求。本文即采用模糊自適應PI對其進行速度控制。在直流無刷電動機控制系統設計中,本文采用雙閉環控制:速度環和電流環。在電流環控制器中,采用傳統的PID控制即能達到滿意的效果;為了提高系統的響應速度和改善控制效果,對速度環采用基于模糊控制理論的模糊自適應PI控制,其系統框圖如圖1所示。

3 模糊控制器的設計
模糊控制器由模糊規則庫、模糊推理機、模糊化接口和解模糊化接口4部分組成。本文設計的模糊控制器是雙輸入、雙輸出模式,其構成如圖2所示。其輸入為電動機的轉速偏差e和轉速偏差變化率ec,輸出為參數Kp、Ki。模糊控制器的輸入量偏差e和偏差變率ec必須經模糊化后,才能成為模糊推理機的輸入量。模糊推理機根據模糊關系推理合成規則[4]Uij=(Ei×ECj)·R計算出輸出量,輸出量Uij仍為模糊變量,要經過解模糊化后才是模糊控制器的實際輸出量Kp和Ki,它們用于實時調節速度PI控制器的比例增益系數Kp和積分增益系數Ki。

3.1 確定輸入、輸出變量的變化范圍和量化因子
本文的控制對象為maxon公司生產的EC45無刷電動機,其基本參數是:額定電壓36 V,額定電流5.24 A,額定功率150 W,額定轉速4 200 r/min,相電感0.26 mH,相電阻2.47 Ω,機械時間常數7.44 ms,轉子慣量119 g·cm2。本文設計的模糊控制器輸入、輸出變量論域均設為[-6,6],用7個語言變量{NL,NM,NS,ZO,PS,PM,PL}表示。隸屬度函數均采用三角形隸屬度函數,如圖3所示。

根據專家經驗,系統轉速偏差e(t)=r(t)-c(t)(其中r(t)為目標轉速,c(t)為實際轉速)達到60 r/min時,就應該是語言值的“PL”,即60×Ke=6,則偏差的量化因子Ke取0.1。對于偏差變化率有:de(t)/dt=dr(t)/dt- dc(t)/dt,因為 dr(t)/dt=0,所以 de(t)/dt=dc(t)/dt,根據電動機的機械時間常數和專家經驗,偏差變化率為80 r/min/s時就應對應語言的“PL”,即80×Kc=6,所以偏差變化率的量化因子Kc取0.075。對輸出變量Kp和Ki確定本文采用“1/4衰減”法來確定其“PL”。根據專家調試經驗,先設Ki=0,從小到大調節Kp,當系統出現等幅振蕩時,記下此時的值Ku,則0.65 ×Ku即為Kp語言值的“PL”。確定Kp后,先使Kp=“PL”,然后從小到大調節Ki,當系統出現等幅振蕩時,記下此時的值Kv,則0.6×Ku即為Ki的語言值的“PL”。進過多次實驗取得,本文Kp的“PL”對應值為2.2,即2.2 ×Kpp=6,則Kp量化因子Kpp取值2.73;Ki的“PL”對應值為 0.46,即0.46×Kii=6,則Ki量化因子Kii取值13。
3.2 設計模糊推理規則
模糊推理規則是模糊控制器的關鍵,其控制規則是建立在長期的控制經驗、專家知識和仿真的基礎之上的。通過模糊推理,得到模糊輸出即模糊解,本文模糊控制器的輸出形式采用增量式輸出。進行模糊推理,要遵守一定的模糊規則,本文的控制對象是直流無刷電動機,應服從如下規則[4]。
(1)當偏差|e|=L時,取較大的Kp,而Ki=0;
(2)當偏差|e|=M且變化率|ec|=L時,應取較小的Kp和中等的Ki;
(3)當偏差|e|=M且變化率|ec|=S時,應取較小的Kp和較小的Ki;
(4)當偏差|e|=S時,應取較大的Kp和Ki。
在上述規則的條件下,根據專家知識和工程師的經驗,本文制定出模糊規則表,如表1、表2所示。
3.3 解模糊化過程

表1 Kp參數模糊規則表

表2 Ki參數模糊規則表
偏差和偏差變化率通過各自的量化因子轉化為論域中的元素,即完成輸入變量的模糊化。通過模糊推理機,得到模糊輸出變量,但這個輸出量必須經過解模糊化后才能作用于控制對象。解模糊化有多種方法,常用的方法有最大隸屬度法、加權平均法、重心法,其中最合理的是重心法,但重心法的計算量較大。由于本文輸入、輸出變量的模糊等級不多,計算量不大,故本文的解模糊化采用重心法來實現。重心法是取模糊隸屬度曲線與橫坐標所圍成面積的重心為模糊推理的最終輸出值。即
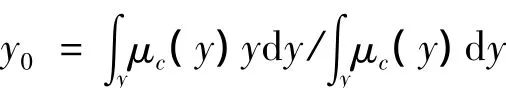
對于n個輸出量化級數的離散論域則為
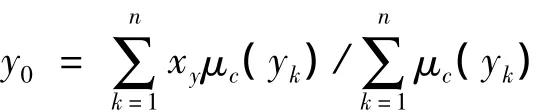

經過解模糊化后,模糊控制器輸出具體的Kp、Ki值給速度控制器,速度控制器是一個PI控制器,模糊控制器就是根據負載和參數的具體變化實時地調整速度PI控制器的Kp、Ki參數值,使系統分工作于最佳狀態。

4 實驗結果
筆者通過實驗把基于模糊自適應PI控制的結果與傳統的PID控制器進行比較,如圖4、圖5所示。從兩圖的比較可以看出當電動機的轉速從0階躍到2 000 r/min時,采用傳統的PID控制模式所需的時間是18 ms,轉速的最大超量為30%。采用模糊自適應PI控制模式時,階躍所需時間為14 ms,即所需時間減少22.2%;轉速的最大超調量為13%,即為傳統PID最大超調量的43.3%。從實驗數據可以得出:模糊自適應PI控制是一種優越的控制模式。
[1]李鐘明,劉衛國.稀土永磁電動機[M].北京:國防工業出版社,1999.
[2]李艷,邵日祥,邵世煌.模糊控制在電氣傳動中的運用現狀及前景[J].電氣傳動,1997,27(2):3 -9.
[3]申志強,鄒繼濤,陳韜,等.張力控制數學模型應用研究[J].華中科技大學學報:自然科學版,2007,32(12):65 -67.
[4]席愛民.模糊控制技術[M].西安:西安電子科技大學出版社,2008.

