二次均勻B樣條曲線的新擴展及應用

郭懷天， 黃有度

（合肥工業大學 數學學院，安徽 合肥 230009）

0 引 言

曲線曲面表示是計算機輔助幾何設計中一個重要的研究課題，其中分段二次均勻B樣條曲線是形式最簡單的也是最常用的樣條曲線之一，然而對給定控制頂點，它的位置是確定的，如果要調整曲線的形狀，需要調整多邊形。有理Bézier曲線和NURBS曲線通過權因子不改變控制頂點，但是它們也存在一些局限性，如計算比較復雜、求導求積不方便等。雖然二次B樣條構造簡單，但其是C連續的而且曲線不能調整，所以使用有一定的局限性。

文獻［1］給出了帶有單個參數的調配函數，也達到了G2、G3連續。但比起本文給出的2個參數來說不是那么靈活；文獻［2］給出了帶有2個三次B樣條調配函數的基；文獻［3］給出帶2個參數的G1連續三次多項式曲線，也增加了曲線設計的靈活性，但是沒有達到G2、G3連續，沒有給出高次的形式，所以不能滿足更高次的連續。本文構造了帶有2個局部參數λi、μi的分段多項式樣條新曲線，它是以二次均勻B樣條曲線為特殊情形，可以有很多種調整方式，具有很好的局部形狀可調整性。

1 二次均勻B樣條曲線的新擴展

1.1 調配函數的構造與性質

定義1 對任意t∈［0，1］，λi，μi∈R，稱關于t的多項式（1）式為帶參數λi、μi的三次調配函數，即

定義2 對任意t∈［0，1］，λi，μi∈R，稱關于t的多項式（2）式為帶參數λi、μi的四次調配函數，即

定理1 對定義1、定義2中調配函數bki（t）（i＝0，1，2；k＝3，4），有如下結論：

（2）當－2≤λi，μi≤1時，t∈［0，1］，bki（t）≥0，i＝0，1，2；k＝3，4。

證明 直接計算可得結論（1），由n次多項式在［0，1］上非負的充分條件可得結論（2），證畢。

事實上，當λi＝μi≠0時，文獻［1］給出的調配函數是本文的特例，λi＝μi＝0時，三次調配函數就退化成二次均勻B樣條基函數。因此，定義1所示三次調配函數是二次均勻B樣條基函數的擴展，同時四次調配函數變成了λi＝μi＝1時的三次調配函數，因而它們都可以看成是二次均勻B樣條基函數的擴展。

定義3 對t∈［0，1］，λi，μi∈R。稱關于t的多項式（3）式為帶參數λi、μi的n次調配函數，即

定理2 對調配函數（3）式，有如下結論：

（2）當－2≤λi，μi≤1時，t∈［0，1］，bni（t）≥0，i＝0，1，2。

證明 同定理1的證明。

1.2 曲線的構造及性質

由定義1可以定義帶有局部形狀控制參數λi、μi的多項式曲線。

定義4 給定控制頂點Pi∈Rd（d＝2，3；i＝0，1，…，n）和節點u0＜u1＜…＜un＋1，對u∈［ui，ui＋1］（i＝0，1，…，n－2），定義多項式曲線段：

其中，t＝（u－ui）／hi；hi＝ui＋1－ui；b3j（t）為（1）式所定義的三次調配函數。定義多項式曲線：

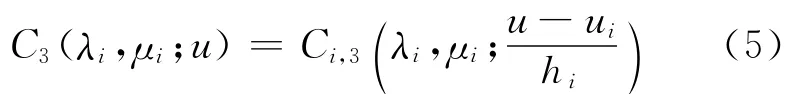
其中，u∈［ui，ui＋1］。

曲線C3（λi，μi；u）是定義在［u2，un－2］上的帶局部參數λi、μi的分段三次多項式曲線，是二次均勻B樣條曲線的擴展。同樣利用四次調配基函數也可以定義四次多項式曲線。

定理3 當λi，μi∈［－2，1］（i＝0，1，…，n－2）時，曲線C3（λi，μi；u）是G1連續的，若曲線每相鄰兩段 Ci，3（λi，μi；t）、Ci＋1，3（λi＋1，μi＋1；t）的形狀 參 數 滿 足 μi＝λi＋1，則 C3（λi，μi；u）是 C1連續的。

證明 由（1）式、（4）式直接計算，可得：

顯然，當λi，μi∈［－2，1］（i＝0，1，…，n－2）時，Ci，3（λi，μi；1）＝Ci＋1，3（λi＋1，μi＋1；0），且 C′i，3（λi，μi；1）＝KiC′i＋1，3（λi＋1，μi＋1；0），其 中 Ki＝（2＋λi＋1）／（2＋μi），故其是G1連續的。若μi＝λi＋1，則 Ki＝1，從而C3（λi，μi；u）是連續的。

綜上所述，可以看出曲線 Ci，n（λi，μi；t）是在曲線Ci，n－1（λi，μi；t）的基礎上，對二次 B 樣條曲線的進一步擴展。

定理4 當λi，μi∈［－2，1］（i＝0，1，…，n－2）時，曲線C4（λi，μi；u）是G2連續的。

證明 由（2）式、（4）式直接計算，可得：

顯然，當λi，μi∈［－2，1］（i＝0，1，…，n－2）時，Ci，4（λi，μi；1）＝Ci＋1，4（λi，μi；0），且 C′i＋1，4（λi＋1，μi＋1；0）＝K1C′i，4（λi，μi；1），其中，進一步計算，得

由定理3、定理4可以看出，當λi＋1、μi滿足一定關系時，C3（λi，μi；u）、C4（λi，μi；u）可以分別達到G2、G3連續，而且，它們也與分段二次B樣條曲線的結構相同。通過定理可知，四次曲線將三次曲線的連續性提高了一階［4－8］。

2 參數的幾何意義

當固定λi，參數μi逐漸增大（或者減小）時，曲線逐漸靠近（或者遠離）控制多邊形的邊，如圖1所示，其中曲線從上到上依次μi＝－1.5，0.1。

同樣當固定μi，參數λi逐漸增大（或者減小）時，曲線逐漸靠近（或者遠離）控制多邊形的邊。

圖1 固定λi＝0.5，μi變化時的曲線

此外，2個參數同時改變可以實現更加靈活的逼近方式，如一個增大一個減小，同時增大或者減小。根據λi、μi的幾何意義，可以根據需要方便地進行曲線設計。而且利用所給調配函數運用張量積的方法可以推廣到曲面，本文不再討論。

3 擴展曲線的應用

利用定義1所給的三次調配基函數給出實例圖形，如圖2所示，所得的分段曲線可以通過參數λi、μi進行調整，當λi＝μi＝0時，即為二次均勻B樣條，四次和更高次的調配可以滿足更好的連續性。圖2中利用了文獻［1］給的控制頂點，即V0＝（0，0），V1＝ （10，20），V2＝ （30，15），V3＝（20，5），V4＝（60，0）。

圖2 參數取不同值的曲線

圖2中，曲線1的λi＝（0.5，－1.5，0.5），μi＝（－1.5，0.5，0.5），i＝0，1，2；曲 線 2 的λi＝μi＝0，i＝0，1，2；曲線3的λi＝μi＝1，i＝0，1，2。

［1］ 劉長明，檀結慶.二次均勻B樣條曲線的擴展［J］.合肥工業大學學報：自然科學版，2004，27（5）：459－462.

［2］ 胡 鋼，劉 哲.三次均勻B樣條曲線的新擴展及應用［J］.計算機工程與應用，2008，44（32）：161－164.

［3］ 殷 明，劉 麗，陳國琪.一類可調控的G1連續分段三次多項式曲線［J］.安徽農業大學學報，2005，32（2）：258－262.

［4］ 施法中.計算機輔助幾何設計與非均勻B樣條［M］.北京：高等教育出版社，2001：166－302.

［5］ 王國瑾，汪國昭，鄭建明.計算機輔助幾何設計［M］.北京：高等教育出版社，2001：18－56.

［6］ 韓旭里，劉圣軍.三次均勻B樣條曲線的擴展［J］.計算機輔助設計與圖形學報，2003，15（5）：567－578.

［7］ 嚴蘭蘭，黃 濤，梁炯豐.3種帶形狀參數的二次三角樣條曲線［J］.合肥工業大學學報：自然科學版，2010，33（4）：632－636.

［8］ 張三元.一種G2連續的二次曲線樣條插值方法［J］.計算機輔助設計與圖形學報，2000，12（6）：419－422.