基于橋墩水痕與推理公式法的橋梁水害預測
吳雪峰,李秀娟
(1.鐵道第三勘察設計院集團有限公司,天津300142;2.天津大學化工學院,天津300072)
在公路、鐵路、城市和農村道路以及水利建設中,為了跨越各種障礙,必須修建各種橋涵,它們往往是保證全線早日通車的關鍵。在經濟上,橋涵造價平均占公路總造價的10%~20%;在國防上,橋梁是交通運輸的咽喉,在需要高速、機動的現代戰爭中,它具有十分重要的地位。因此,為了保證正常的交通運輸,必須保證橋涵安全可靠[1]。
1991年Shirhole等人對美國已毀壞的823座橋梁的毀壞原因進行分析,得到的結果見表1。
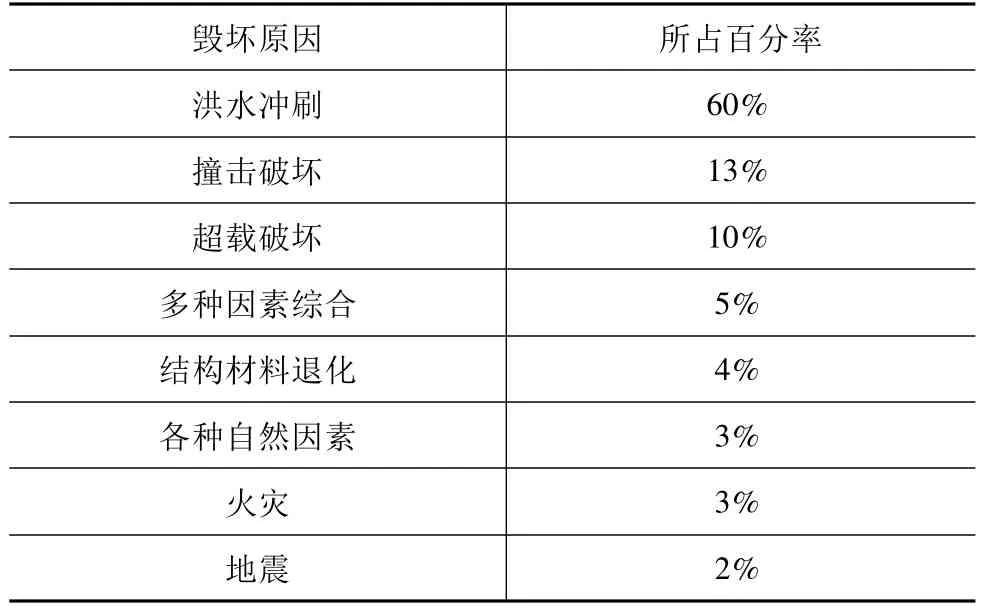
表1 美國橋梁毀壞原因分析[2]
可見,在美國水毀橋梁是超載毀壞橋梁的6倍,地震破壞橋梁的20倍。
我國地處亞歐大陸東側,跨高、中、低三個緯度區,季風特點十分顯著,降水在季節分布上不均勻。全年的降水量大部分集中在夏季濕潤高溫的時期,且多以暴雨形式出現,容易形成洪澇災害。
因此,我國橋梁歷來遭受洪水破壞的情況同樣嚴重。據交通部不完全統計,1977年9省(區)水毀橋梁975座,總長5 150 m;局部水毀橋梁134座,總長3 481 m;水毀涵洞2 756個,水毀損失約5 400萬元;1995~1997年,我國平均每年公路水毀的直接經濟損失達52億元,其中水毀橋梁達3 945座;2006年,全國公路水毀的直接經濟損失已達63億元,其中毀壞橋梁達2 583座。
可見,水毀是世界各國橋梁面臨的最嚴重的自然災害。如何在洪水發生前對橋梁即將面對的狀況作出有效的預測,具有重大現實意義。
1 橋梁水毀原因
橋梁水毀的原因從水文角度看,最重要的有兩個[3]。
1.1 橋梁的設計流量選取不合理
中小流域橋梁設計流量的確定,往往在缺少相關水文資料條件下進行,一般采用成因分析的方法來推算橋梁設計洪水。前人在中小流域橋梁水文設計研究中已提出了許多方法,但這些方法大部分是經驗或半經驗公式,計算方法不甚完善且計算繁瑣,使孔徑設計遇到了許多困難。設計流量確定過大,橋梁修得過大,是一種浪費;設計流量確定過小,橋梁跨徑或基礎埋置深度不夠,建橋后當洪水到來時不能及時泄洪就會發生水害。
1.2 建橋后水文條件的變化
既有橋修好后,生態環境發生了巨大變化,導致橋梁水文設計參數發生了變化,由原來的設計參數得出的設計流量已經不能滿足現在泄洪的需要。如:大地植被在修橋前后發生了較大的變化,在設計時看來不大的降雨,到現在可能形成較大的洪水,有的甚至威脅橋梁的安全;非法挖沙使河床變得粗糙,改變了糙率系數,削弱了橋梁的過洪能力,致使橋梁容易出現事故。
2 推理公式法[3]、[4]
中小流域河流及溝渠的橋涵的設計流量,一般由暴雨資料來推求。從洪水的成因出發,涉及暴雨、產流和匯流過程,通過一定的概化條件,可以計算出橋位斷面的洪峰流量。在徑流成因公式的基礎上進一步簡化,便可得到計算洪峰流量的推理公式。
推理公式法形式多樣。其中,我國水利科學研究院水文研究所的推理公式法應用較為普遍。該推理公式法作了如下假定。
(1)假定流域的降雨過程與損失過程的差為產流過程,并把匯流時間內所產生的徑流概化為強度不變的過程;
(2)把匯流面積曲線概化成矩形;
(3)假設暴雨和洪水同頻率,與流量有關的其他參數不再有頻率的概念。
依據上述假定,頻率為p的設計流量(m3/s)
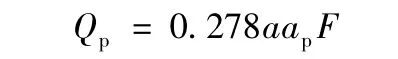
式中:0.278為流量與暴雨強度單位統一的乘子;
ap為頻率為p的暴雨強度(mm/h);F為流域面積(km2);
a為洪峰流量系數。
暴雨強度ap(mm/h)與雨力sp(mm/h)的關系為:
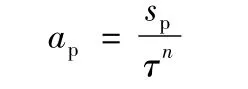
式中:n為暴雨衰減指數;
τ為流域匯流時間(h)。
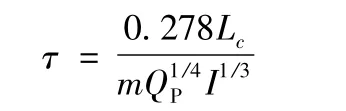
式中:m為流域匯流參數;
Lc為流域全長(km);
I為沿最遠流程的平均坡度。
據產流歷時tc與流域匯流時間τ的關系,匯流可分為全面匯流與部分匯流兩種情況。
(1)全面匯流
tc≥τ時,出口斷面處的洪峰流量由全流域匯流形成。
(2)部分匯流
tc<τ時,出口斷面處的洪峰流量由部分面積匯流形成。
令f為形成洪峰流量的部分流域面積(如圖1所示),在求得ltc后,可在流域地形圖上取得相應的最大面積,即為f。
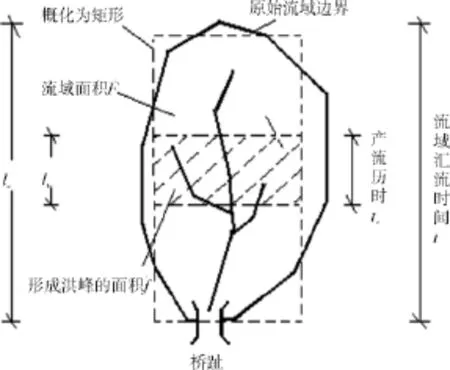
圖1 部分匯流面積示意
根據推理公式法假定(2),部分面積匯流形成的洪峰流量
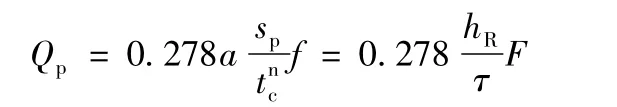
式中:hR為由主雨峰產生的徑流深(mm)。
推理公式法的理論依據是等流時線原理[5]。根據推理公式法可以簡便地求出某一暴雨對應的流量,這對于缺乏流量觀測資料的中小流域橋梁具有十分重要的意義。但對于大多數中小流域橋梁,流域面積較難獲取,這無疑給推理公式計算洪峰流量帶來一定困難。
3 基于橋墩水痕的換算流域面積
3.1 橋墩水痕
大量調查發現,橋梁在歷年洪水作用下,由于洪水的浸泡沖刷,導致墩臺材料某些成分流失,從而在墩臺上留下一條明顯的痕跡,而且水位越高,痕跡越清晰,可靠度越高。
圖2為京廣線橋1538橋墩上遺留下來的歷史水痕[6],圖上標注的數據為實測的歷史水痕的高程(單位:m)。

圖2 京廣線橋1538橋墩水痕圖
圖2中的一條水痕記錄了歷史上一次暴雨時的水位。由于機構調整,人員變動,京廣線橋1538的可靠記錄只保留有6項。表2是圖2歷史水痕實測與記錄對照。
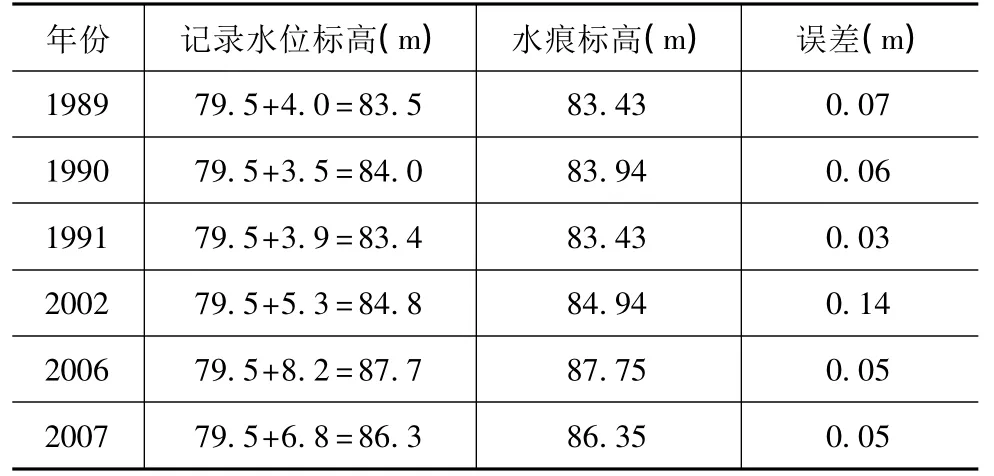
表2 歷史水痕實測與記錄對照
可以看出,歷史洪水的當時記錄與現時水痕實測值的誤差較小,利用實測水痕是可靠的。這樣,對于偏遠地區缺乏水文資料的大量中小橋,可以利用橋墩水痕記錄的水位標高,結合當地的降雨資料,利用推理公式法求出流域面積等信息。
3.2 換算流域面積
流域面積是一個重要的地貌參數,幾乎所有的流域地貌參數都與流域面積有一定關系。為敘述方便,本文將由暴雨平均強度及水痕對應洪峰流量直接根據推理公式法推求的流域面積稱為換算流域面積,記作Fe。它的意義在于將暴雨損失和地下徑流對橋位斷面流量的影響都歸到換算流域面積Fe中進行考慮。
設橋墩水痕標高為Hmax,由謝才-滿寧公式,橋墩水痕相對應的洪峰流量

式中:1/n為糙率系數,其中n為糙率;
R為水力半徑,R=ω/p(m),p為過水斷面濕周;
ω為流水斷面面積(m2)。
由推理公式法,流域的換算流域面積
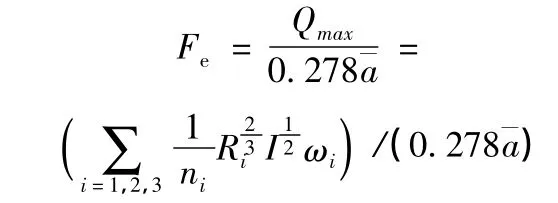
4 實例分析
江西境內有拱橋一座,左河灘與右河灘的糙率系數均為12,主河槽的糙率系數為20,匯流參數m=1.2,橋位斷面以上主河道長度L=32.8 km,橋前的水面坡度I=4‰,每孔橋墩間距為20.6 m,橋梁與水流正交。該橋的橋址處河床斷面如圖3所示。
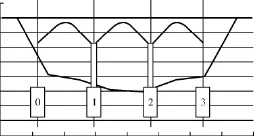
圖3 橋址處河床斷面
由歷史橋墩水痕,該橋所在流域的歷史日最大暴雨量與其相應的水位值見表3。
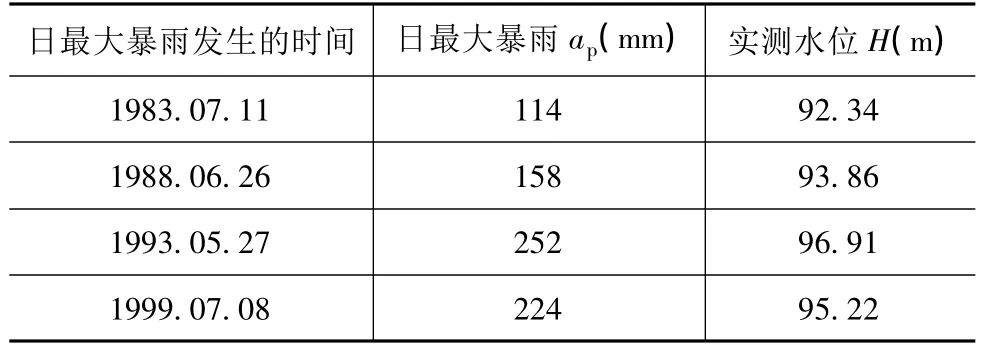
表3 日最大暴雨量與橋墩水痕記錄的水位關系
1993年橋墩水痕標高為96.91 m,與之相對應的日最大暴雨為252 mm,根據暴雨強度公式,查地方水文手冊取暴雨衰減指數為0.65,可得最大匯流時間內平均暴雨強度為18.6 mm/h。利用謝才-滿寧公式計算與橋墩水痕對應的洪水洪峰流量為534.42 m3/s。根據推理公式法計算橋位斷面以上流域的換算流域面積。
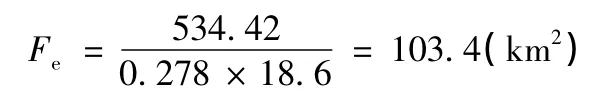
2008年9月某日根據橋位上游水文站對降雨的觀測,產流時間3 h內的暴雨量為72 mm,屬于部分匯流情況,根據推理公式法計算洪峰流量
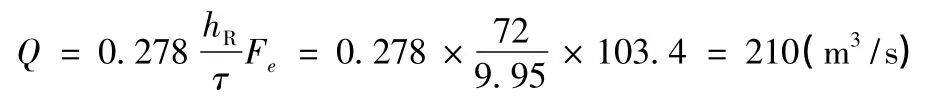
流域最大匯流歷時
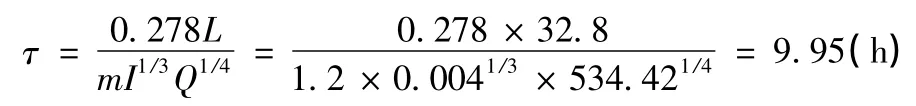
經現場觀測,此次暴雨在橋位處形成的洪水洪峰流量約為220 m3/s,與預測的210 m3/s比較接近。
5 結論
(1)從歷史橋墩水痕出發,利用推理公式法推求橋位以上流域的換算流域面積。避免了為獲取相關流域資料預測橋梁水害而必須進行的繁重外業,大大降低了外業勞動的強度。
(2)換算流域面積是本文提出的新概念,換算流域面積的提出解決了過去進行流域匯流計算時必須計算暴雨損失、劃分地面地下徑流等難題,利用換算流域面積來考慮暴雨損失、地下徑流等對洪峰流量的影響,提高了預測效率。
(3)根據預報暴雨量,可以很方便地利用本文方法進行流量預測,從而對既有橋梁安全作出及時準確的預測。
[1]范立礎.橋梁工程[M].北京:人民交通出版社,2001
[2]凌天清.公路與橋梁抗洪分析[M].北京:人民交通出版社,1999
[3]文雨松.橋涵水文[M].北京:中國鐵道出版社,2005
[4]鐵道部第三勘測設計院.橋渡水文[M].北京:中國鐵道出版社,1999
[5]葉鎮國.土木工程水文學[M].北京:人民交通出版社,2000
[6]文雨松.基于橋墩歷史水痕與氣象預報的中小橋水害預測[J].鐵道學報,2010,32(2):141-144

