高超聲速彈性飛行器后體/外噴管建模與分析

祝強軍, 唐碩, 譚藝明

(西北工業大學 航天學院, 陜西 西安710072)

高超聲速彈性飛行器后體/外噴管建模與分析

祝強軍, 唐碩, 譚藝明

(西北工業大學 航天學院, 陜西 西安710072)

考慮到全尺寸吸氣式高超聲速飛行器的機體彈性彎曲振動極易被激發,提出了一種包含機體彈性彎曲影響的外噴管建模和分析方法。該方法首先用虛擬激波膨脹波法確定剪切層的位置,然后用影響系數法求解外噴管中的準一維流,并用活塞理論修正后體下表面的壓力。用該方法對一個全尺寸吸氣式高超聲速飛行器的后體/外噴管進行了仿真分析,結果表明,僅考慮低頻、小振幅的后體彈性彎曲運動對外噴管性能的影響并不顯著。

高超聲速; 彈性; 外噴管; 影響系數; 活塞理論

引言

對于全尺寸的吸氣式高超聲速飛行器,其低階彈性彎曲模態頻率通常很接近其剛體運動頻率,激勵剛體運動的控制輸入極易激發機體的低階彈性彎曲模態。吸氣式高超聲速飛行器的典型特點是乘波體機體和超燃沖壓發動機一體化設計[1-2],用飛行器的后體下表面和膨脹過程中形成的自由射流邊界構成噴管,并稱其為單面噴管、自由膨脹噴管或者外噴管[3]。自由射流邊界又稱為剪切層,它是發動機尾氣與自由流的靜壓達到平衡時的邊界。如果飛行器機體發生彎曲振動,由于后體下表面的形狀發生變化,剪切層也將發生變化,因此外噴管的膨脹性能將會改變,最終導致尾氣對后體下表面作用力的大小和方向發生變化。因此,建模分析機體發生彈性振動對后體氣動和推進特性產生怎樣的變化,對于設計全尺寸的吸氣式高超聲速飛行器具有特別重要的指導意義。

D K Schmidt[4]最先建立了包含機體彈性變形影響的吸氣式高超聲速飛行器動力學解析模型。Schmidt將飛行器看作一個倒三角形,機體彈性變形用前體和后體繞倒三角頂點的轉動來表示,后體壓強用一個近似公式表示。用Schmidt的解析模型來分析吸氣式高超聲速飛行器后體氣動和推進特性存在下列不足之處:首先,飛行器的真實振型與繞倒三角頂點的轉動可能有較大差異,Schmidt沒有明確給出使用這種簡化振型的依據;第二,后體壓強近似公式不能用于分析飛行器機體彈性變形引起剪切層變化和尾氣沿后體非理性膨脹的情況。Bolender和Doman[5]擴展了Schmidt的飛行器模型,使其包含超燃沖壓發動機通道,但是對飛行器后體的建模仍然采用Schmidt的近似公式。

針對前人工作存在的上述不足,本文以一個全尺寸吸氣式高超聲速飛行器為研究對象,建模分析了機體彈性彎曲振動對飛行器后體氣動和推進性能的影響。機體彈性彎曲振動采用更真實的兩端自由梁模型。提出了先用虛擬激波膨脹波理論確定剪切層位置,然后用影響系數法求解準一維流,并用活塞理論修正后體壓強的分析方法。最后用一個具體的算例分析了后體彈性彎曲對外噴管性能的影響。

1 機體縱向彈性彎曲振動的描述

吸氣式高超聲速飛行器的細長形機體可以近似看作兩端自由的彈性梁,其縱向彎曲方程為:

(1)

式中,w(x,t)為彎曲位移;EJ(x)為彎曲剛度;m(x)為單位長度的質量;p(x,t)為載荷集度。利用自由振動模態函數,式(1)的解可用分離變量法表示為:

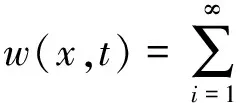
(2)

式中,φi(x)為第i階自由振動模態函數;ηi(t)為第i階模態的廣義坐標。將式(2)代入到式(1)中,考慮結構阻尼的影響,增加結構阻尼項后可得:

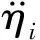
(3)

式中,ξi為結構阻尼比,通過對實際結構做實驗可以測出,其值通常小于0.1。忽略結構阻尼的影響,式(3)的通解為:

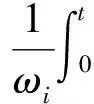
(4)

在飛行過程中,如果氣動載荷與機體彈性運動發生耦合作用時,其彎曲振動可能會出現振幅不衰減的情況。考慮臨界情況,即機體作簡諧振動的情況下對吸氣式高超聲速飛行器壓縮系統產生什么影響,此時廣義坐標表示為:

ηi(t)=ηi(0) cos(ωit)

(5)

2 后體/外噴管分析方法

吸氣式高超聲速飛行器后體下表面和位于其下方的剪切層構成了發動機的外噴管。高溫、高壓尾氣將在外噴管中繼續膨脹。因此,建模分析機體彈性振動對后體/外噴管的影響時,首先需要確定剪切層的位置,然后對外噴管中的流動進行分析。

2.1 虛擬激波膨脹波法——確定剪切層位置

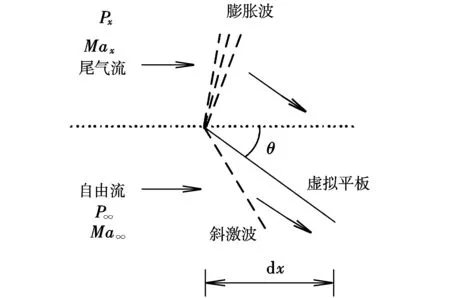
圖1 確定剪切層位置的虛擬激波膨脹波法

在外噴管自由射流邊界兩側的流體具有相同的靜壓和速度方向,但是速度的大小并不相同。由于自由射流邊界存在很大的速度梯度,通常將其稱為剪切層。剪切層兩側流體的法向速度為零,因此剪切層可以看作是虛擬的不可穿透的固壁面。將外噴管沿流動方向劃分為若干微段,當每一微段都足夠短時,該微段的剪切層可用一平板代替。如圖 1所示,對于某一外噴管微段,尾氣將從主流方向通過膨脹波偏轉羽流角θ轉向虛擬平板方向;自由流將通過斜激波偏轉同樣大小的θ轉向虛擬平板方向。這個θ可根據尾氣的靜壓等于自由流靜壓來確定。具體來講,先假定一個θ,然后求解尾氣流偏轉θ的Prandtl-Meyer膨脹波方程,求解自由流偏轉θ的斜激波方程,如果尾氣流和自由流的靜壓不同,則重新選擇θ,重復上述過程直到獲得某個θ使得尾氣流和自由流的靜壓相等。如果尾氣流與自由流的壓強比高于某個極限值,那么使尾氣流與自由流壓強相等的偏轉角就可能接近90°或者不存在。如果θ接近90°,則外噴管的面積變化為無窮大,為了保證準一維流假設的合理性,壓強比高于極限值時可以設置θ為75°[6]。

2.2 影響系數法——求解外噴管中的準一維流

驅動準一維流參數變化的因素有:截面積變化、壁面摩擦、熱傳遞、機械功、質量注入、體積力、化學反應等。僅單個因素作用的簡單流通常可以獲得解析解,而多個因素同時作用的復雜流通常需要數值求解流體控制微分方程組。外噴管中的流動可看作具有面積變化和壁面摩擦的復雜流。將外噴管沿流動方向劃分為若干足夠短的微元段,然后利用微分形式的流體控制方程組對微元逐段求解就可得到外噴管流場的解。對圖 2所示的微元控制體,Shapiro[7]推導了流體控制方程的微分形式,并以式(6)～式(8)中的影響系數的形式給出。

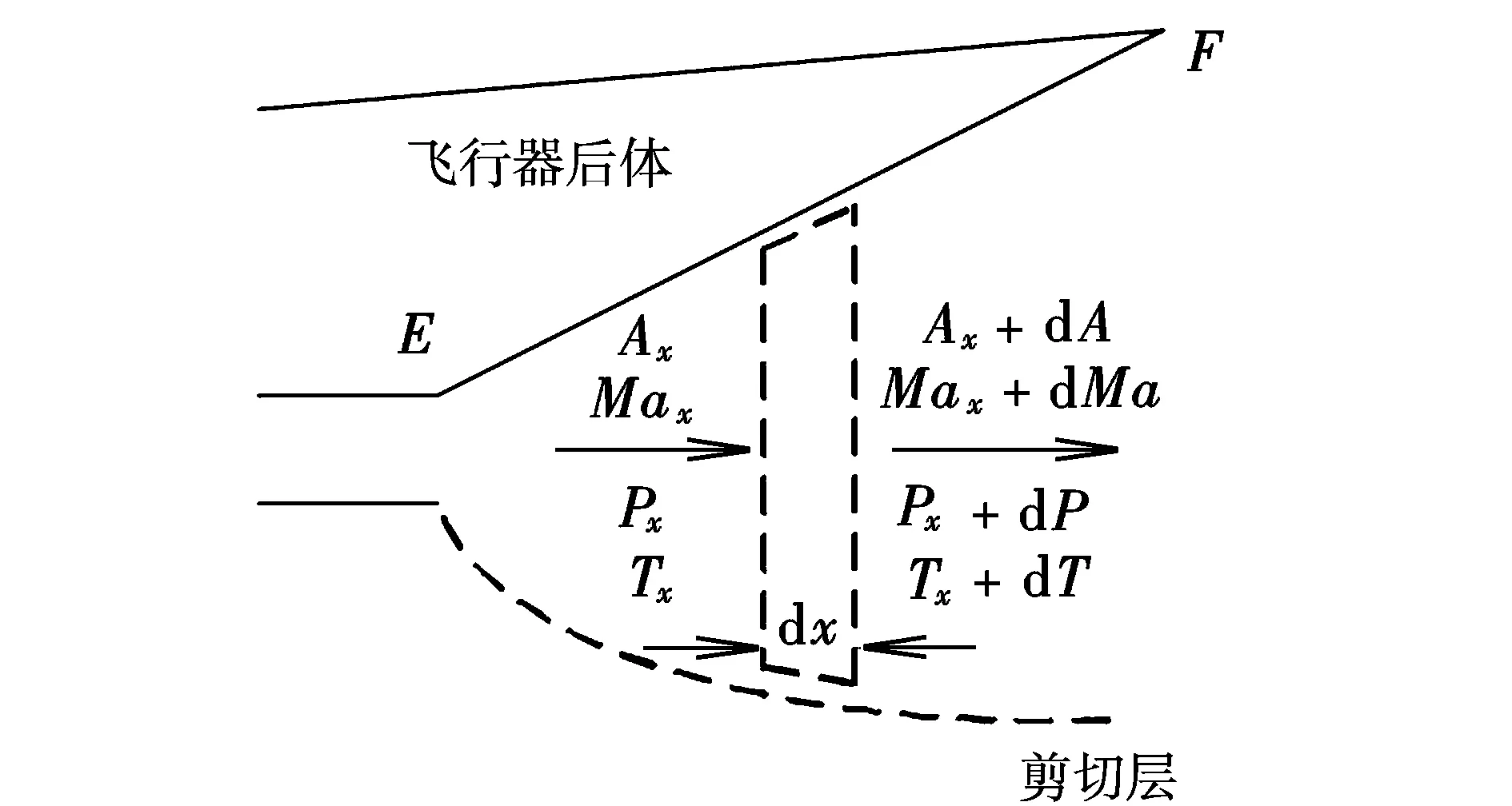
圖2 外噴管的微元控制體

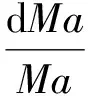
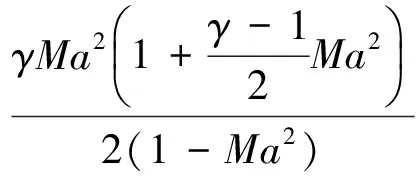
(6)

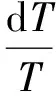
(7)

(8)

式中,γ為尾氣流的比熱容比;dA為微元面積變化;Cf為壁面摩擦系數,按文獻[6]建議設為0.005;D為外噴管的水力半徑；P和T分別為壓強和溫度。

dA=dx(tanθ+tanθn)

(9)

式中,θn為后體傾斜角。

D=4Ax/Px=4hx

(10)

式中,Ax為坐標為x處的外噴管橫截面積;Px為該截面周長中存在壁面摩擦的那部分長度。

2.3 活塞理論——考慮彎曲速度對壓強的影響

上述分析只考慮了機體彎曲位移引起外噴管截面積變化所產生的影響。由于機體在彎曲振動過程中,彎曲速度會對外噴管的尾氣流產生擾動,因此需要對作用于后體下表面的壓強進行修正。外噴管中尾氣流的速度為超聲速流,而低頻彎曲振動的速度通常很小,在此前提下,可以假設后體下表面某一點的壓強只與該點的下洗速度有關。假設外噴管中的準一維流是沿發動機軸線方向的,后體彎曲速度與該方向垂直,于是后體下表面尾氣流的下洗速度為:

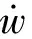
(11)

考慮到后體彎曲速度產生的下洗影響,可用活塞理論對后體壓強進行修正。活塞理論認為,后體下表面某點的壓強與該點的下洗速度有關,可用活塞在一維管道中運動時,其所受到的壓強與其運動速度的關系來比擬。活塞理論給出壓強公式為:

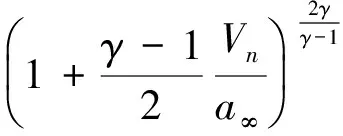
(12)

式中,P∞和a∞分別為未受彎曲速度擾動的尾氣流的壓強和聲速。

3 算例與分析

3.1 基本參數

以一個總長為30.5 m的全尺寸吸氣式高超聲速飛行器為例,假定其在高度30 km、Ma=7 巡航飛行時,機體受到某種擾動作用而發生彈性彎曲諧振,并假設機體振動引起的發動機入口條件的變化可以通過發動機的控制來補償,因此可以認為外噴管入口處的尾氣流動參數保持不變(具體見表1)。在此前提下,計算和分析后體的氣動和推進特性。

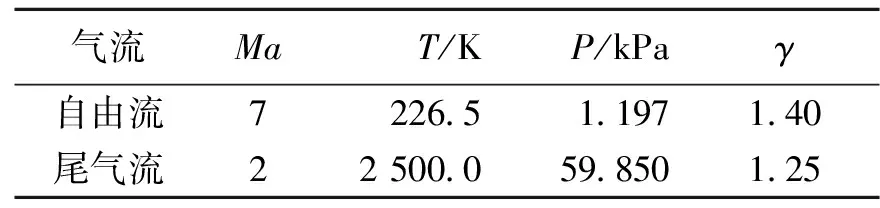
表1 外噴管的入口條件

3.2 振動位移的影響

后體發生彈性振動將引起剪切層位置的變化,進而引起外噴管橫截面積的變化。一般來說,剪切層的位置主要取決于其起始位置,沿著x方向跟隨后體振動而上下移動,但是移動量要小于后體的移動量(見圖 3)。因此當后體上移時外噴管的橫截面積增大,從而使馬赫數增大,溫度和壓強減小;反之,后體下移時橫截面積減小,從而使馬赫數減小,溫度和壓強增大(見圖 4)。

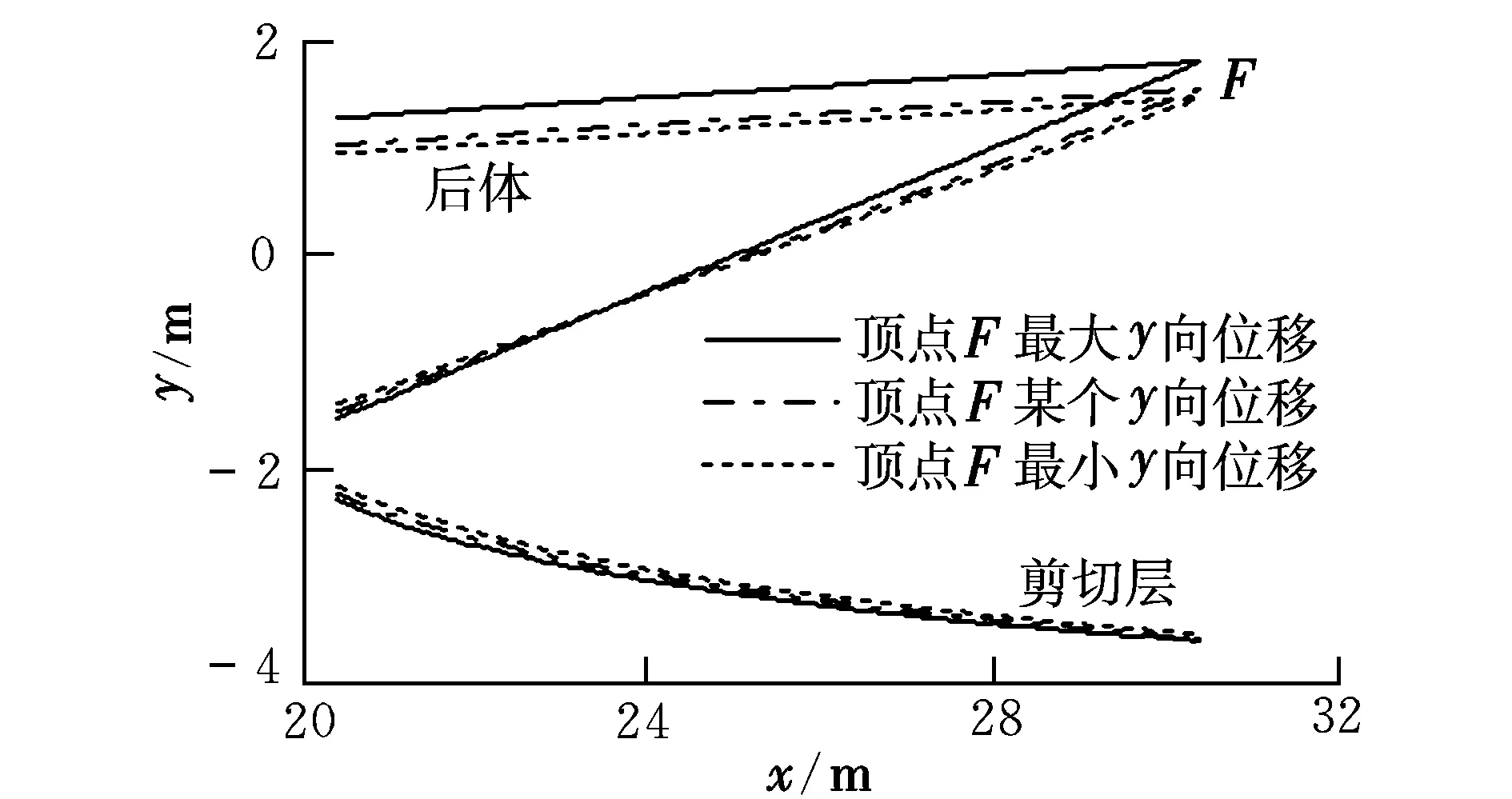
圖3 后體/外噴管位置變化

圖4 外噴管參數變化

圖 4還給出了分別用Schmidt預測方法[4-5]和本文方法得到的飛行器后體下表面的壓強分布曲線。由圖可見,Schmidt預測的壓強要明顯低于本文計算得到的壓強值。這是因為Schmidt的后體壓強分布公式是根據外噴管理想膨脹得到的,而高超聲速推進系統的外噴管通常工作在欠膨脹狀態。另外,彈性變形引起的壓強分布變化量遠小于Schmidt預測的誤差量,從這個意義上看,用Schmidt預測法來考慮彈性變形影響是值得商榷的。

3.3 摩擦和振動速度的影響

圖 5所示的是機體振動頻率為25 Hz、振幅為0.6%總長時,分別考慮彈性振動位移影響、彈性振動位移加上摩擦作用影響、彈性振動位移和速度加上摩擦作用影響三種情況下,后體壓力和壓心的變化情況。

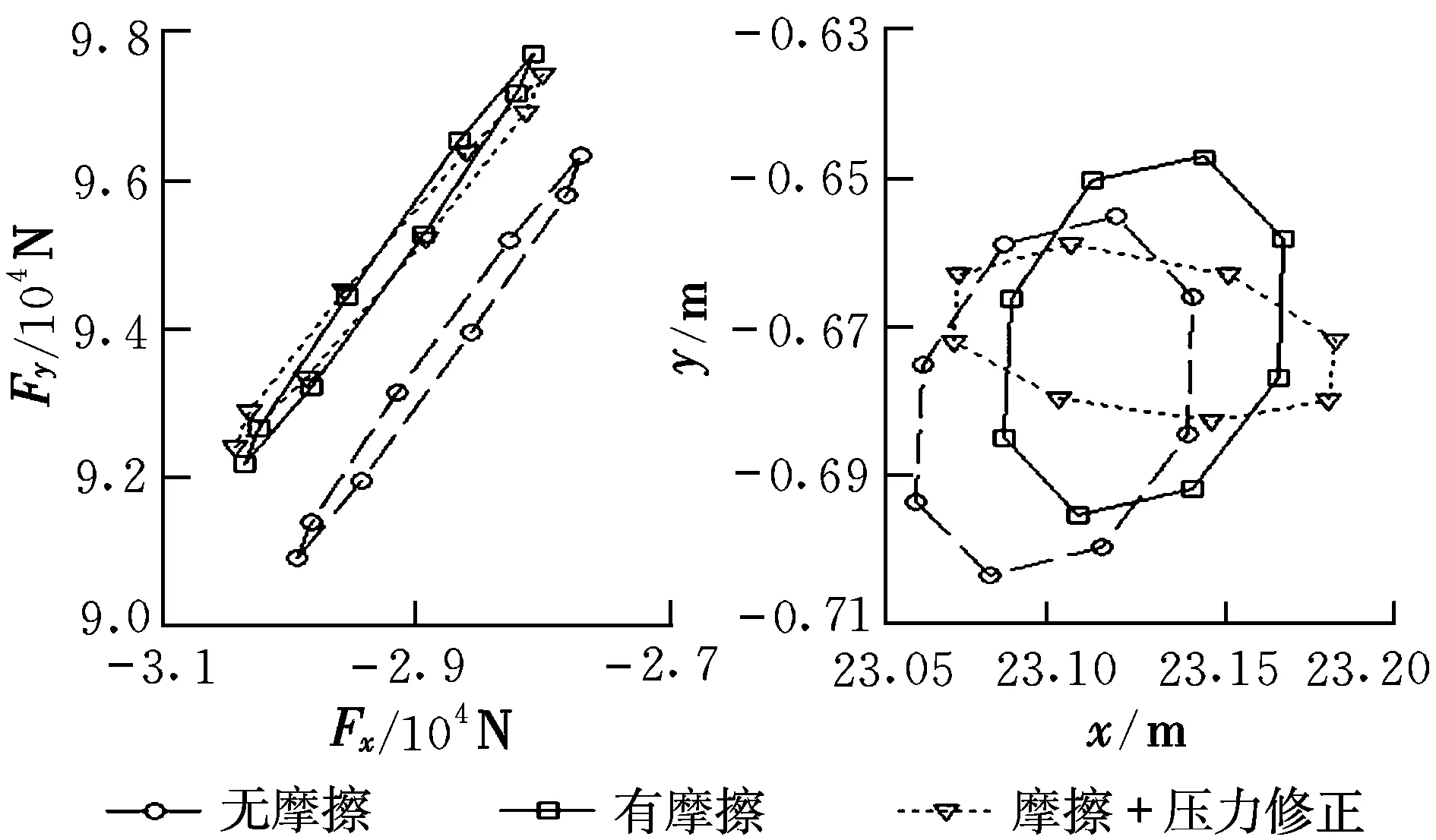
圖5 后體壓力矢端軌跡和壓心軌跡

由圖5可知,在尾氣流向外噴射過程中,由于后體下表面的摩擦作用,尾氣作用于后體的壓強在有摩擦情況比無摩擦情況下沿x方向下降要緩慢些。與無摩擦情況相比,有摩擦情況下尾氣作用于后體壓力要大一些,壓心位置靠后一些。如果再考慮到彎曲速度的影響,利用活塞理論對后體下表面的壓力進行修正,后體壓力變化量并不大,但是壓力的相位會產生一個超前量,壓心在y方向的變化范圍變小。

圖6所示的是考慮后體摩擦作用和忽略后體摩擦作用情況下的總壓比變化情況。由圖6可知,振動引起的總壓比變化相對較小,而摩擦作用引起的總壓比下降十分明顯。

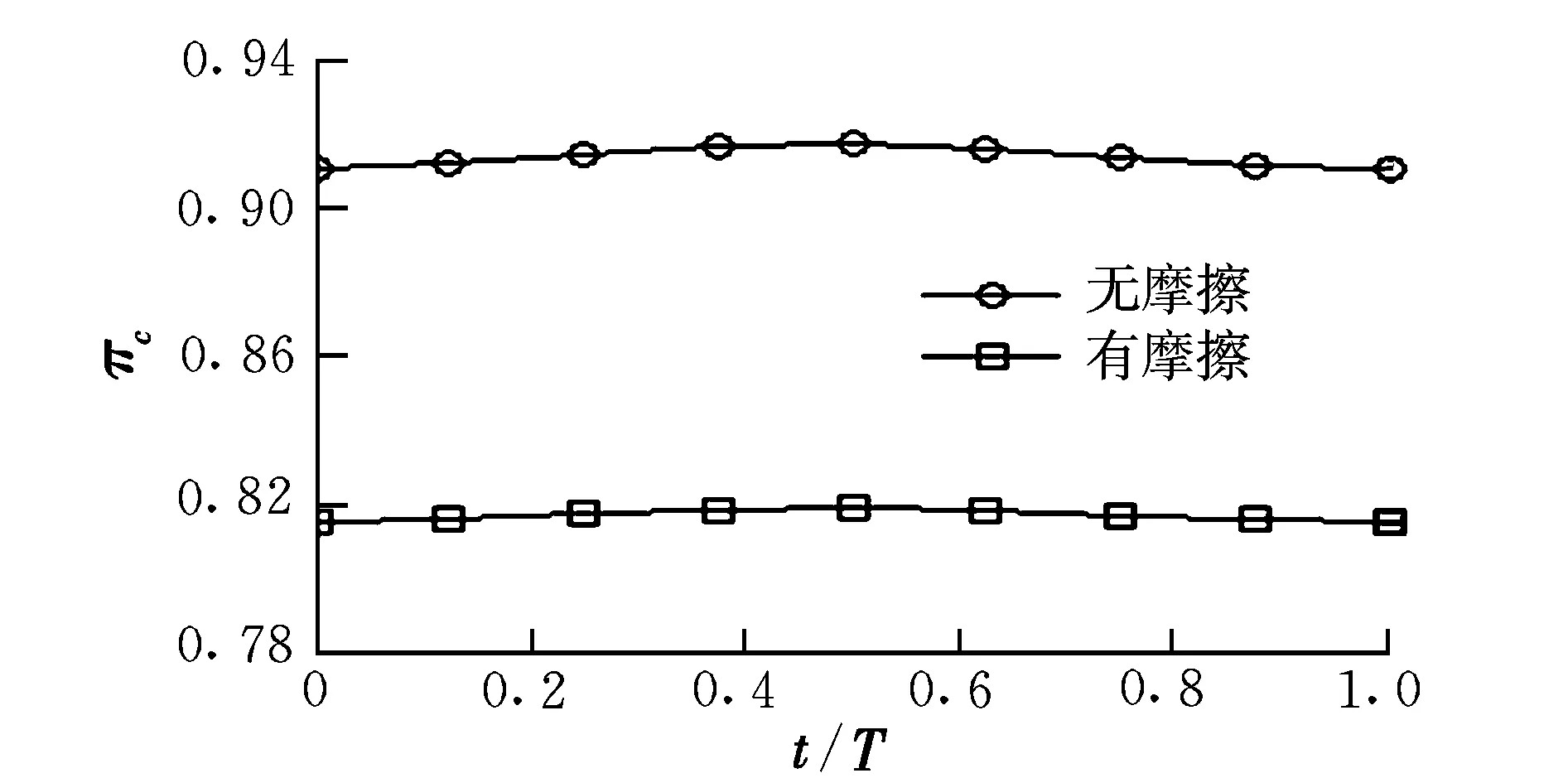
圖6 總壓比變化

3.4 機體振動頻率的影響

圖 7所示的是機體振幅為0.6%總長時,振動頻率分別為5 Hz,25 Hz和50 Hz情況下的后體下表面壓力和壓心在振動過程中的變化曲線。

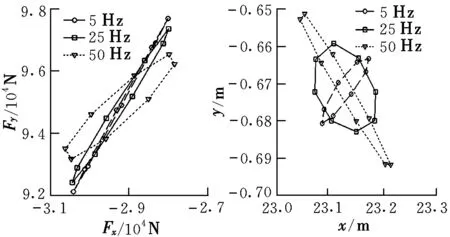
圖7 不同頻率的后體壓力矢端軌跡和壓心軌跡

從圖 7可以看到,隨著振動頻率的增大,彎曲速度的影響不斷增強,y方向壓力變化范圍趨于縮小,但是壓心位置變化范圍更大了。

3.5 機體振動幅值的影響

圖8所示的是機體振動頻率為25 Hz時,振幅分別為0.4%,0.6%和0.8%總長的情況下的后體下表面壓力和壓心在振動過程中的變化曲線。由圖 8可以看到,后體下表面壓力與壓心位置變化范圍幾乎與振幅成正比增大。

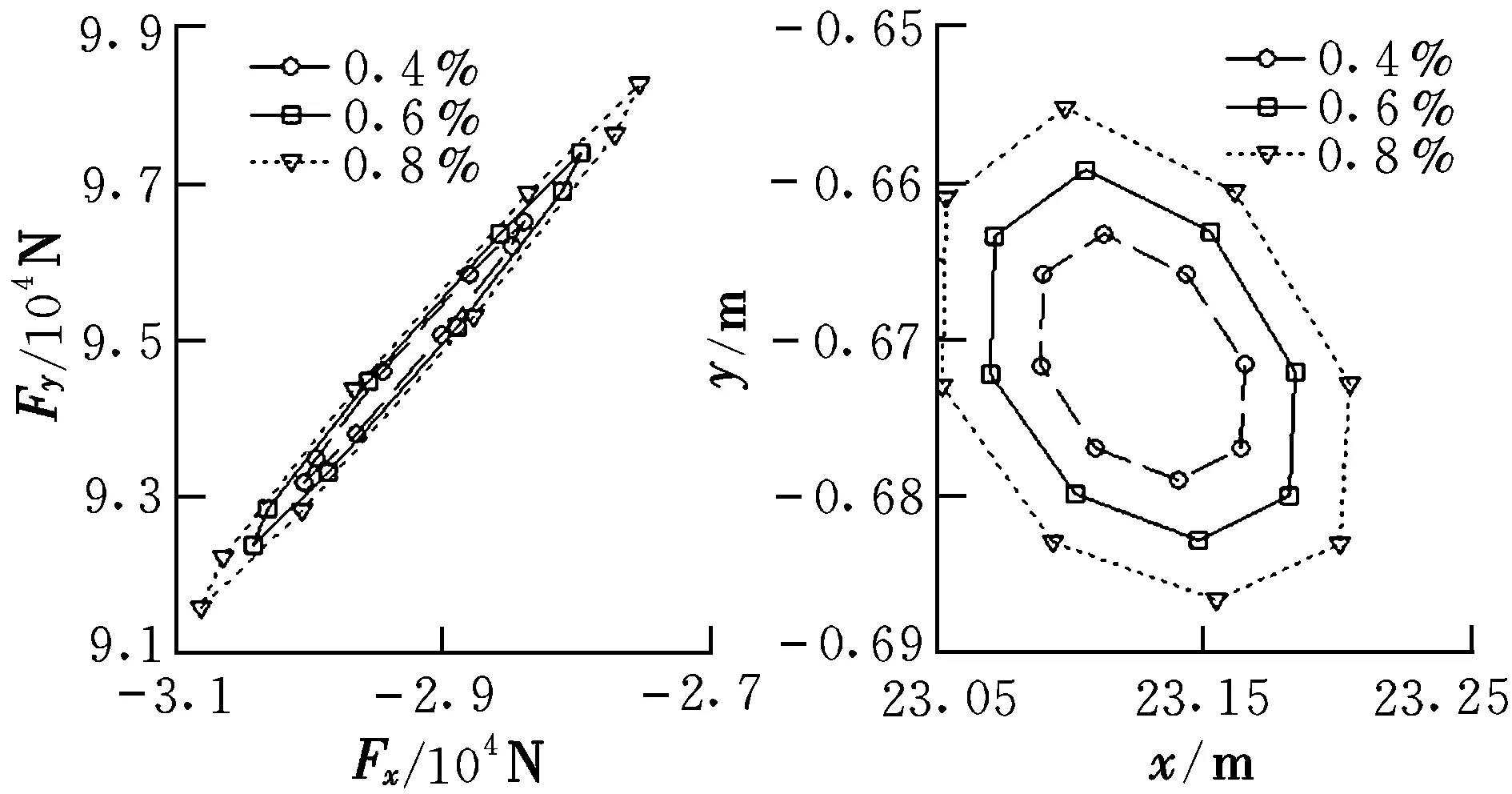
圖8 不同振幅的后體壓力矢端軌跡和壓心軌跡

4 結論

通過對吸氣式高超聲速彈性飛行器的后體/外噴管的建模和分析,可得到下列結論:

(1)對于全尺寸的吸氣式高超聲速飛行器,其低階的機體彈性彎曲振動極易被激發。對于所關心的低頻、小振幅機體彈性彎曲振動而言,如果單獨考慮后體/外噴管在振動過程中的影響,可以發現其影響并不是特別顯著;

(2)文中的算例是在一階固有振動情況下計算得到的,在二階固有振動情況下變化趨勢將有所不同,但只要是在小振幅條件下,后體彈性運動的影響同樣不是那么顯著;

(3)文中通過假設后體/外噴管入口參數在機體振動過程中保持不變,考察了后體彈性彎曲振動產生的影響。由于吸氣式高超聲速飛行器機體/發動機一體化設計的特點,如果考慮到前體彎曲產生的擾動傳遞到后體所產生的影響,則還需要進一步分析。

[1] Javaid K H,Serghides V C.Airframe-propulsion integration methodology for waverider-derived hypersonic cruise aircraft design concepts[C]//The 42nd AIAA Aerospace Sciences Meeting and Exhibit. USA:Reno,Nevada,2004:1-10.

[2] Lewis M J.A hypersonic propulsion airframe integration overview[C]//The 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit.USA:Huntsville,Alabama,2003:1-11.

[3] Schmidt D K,Mamich H,Chavez F R.Dynamics and control of hypersonic vehicles the integration challenge for the 1990’s[C]//The 3rd AIAA International Aerospace Planes Conference.USA:Orlando,FL,1991:1-10.

[4] Chavez F R,Schmidt D K.Analytical aeropropulsive/aeroelastic hypersonic-vehicle model with dynamic analysis[J].Journal of Guidance,Control,and Dynamics,1994,17 (6):1308-1319.

[5] Bolender M A,Doman D B.Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J].Journal of Spacecraft and Rockets,2007,44 (2):374-387.

[6] Brewer K M.Exergy methods for the mission-level analysis and optimization of generic hypersonic vehicles[D].Blacksburg,Virginia:Virginia Polytechnic Institute and State University,2006.

[7] Shapiro A H.The dynamics and thermodynamics of compressible fluid flow[M].New York: John Wiley and Sons,1953.

Modelingandanalyzingtheafterbodyexternalnozzleofaflexiblehypersonicflightvehicle

ZHU Qiang-jun, TANG Shuo, TAN Yi-ming

(Collage of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China)

To investigate the influence of airframe bending vibration on external nozzle for full-scale airbreathing hypersonic flight vehicles (AHFV), a new method is developed for modeling and analyzing the external nozzle of AHFVs under the airframe vibration. The first step of this method is to determine the shear layer position using virtual shock-expansion wave method. After that, the flow in the external nozzle modeled as quasi-one dimensional flow is solved using the influence coefficients method, and the pressure on the lower surface of afterbody is modified by the piston theory. To analyze the influence of airframe bending vibration on external nozzle performance, a simulation is carried out using the new developed method. The results show that the change of an external nozzle performance is not so remarkable, as long as the airframe bending motion is in the range of low frequency and small amplitude.

hypersonic speed; flexibility; external nozzle; influence coefficien; piston theory

2011-03-11;

2011-07-27

祝強軍(1982-)，男，浙江江山人，博士研究生，研究方向為高超聲速飛行器動力學與控制。

V411

A

1002-0853(2012)01-0048-05

(編輯：姚妙慧)