邊坡穩定的有限元分析

藍 杰 劉玉梅

在公路建設中，不可避免的將修建邊坡。邊坡的穩定性關系到道路工程的施工安全、建設成本和運營安全。因此，保證邊坡的穩定性對于防災減災、工程建設具有重要意義。目前，邊坡穩定性的分析方法有兩類:極限平衡方法和數值分析方法。極限平衡方法是以Mohr-Coulomb抗剪強度理論為基礎，將滑坡體劃分成若干垂直條塊，建立作用在垂直條塊上的力的平衡方程式，求解邊坡的安全系數。該方法物理概念明確，通用性強，但不能考慮土體本身的應力—應變關系，因此不能真實反映邊坡失穩時的應力場和位移場。隨著計算機硬件、軟件的飛速發展，采用更完備的方法分析邊坡穩定問題成為了可能，由此產生了邊坡穩定的數值分析方法，該類方法不僅滿足邊坡力的平衡條件，并考慮了土體的應力—應變關系，使得結果更為精確可信。

筆者根據設計工作中的工程實例，采用數值分析方法中的有限元強度折減法，運用通用有限元軟件ANSYS對某高速公路的邊坡進行分析。

1 有限元模型的建立

1.1 屈服準則和安全系數的定義

采用ANSYS軟件建模時，采用理想彈塑性模型，即土體和巖石等采用DP材料選項，符合Drucker-Prager屈服準則，該準則即為:

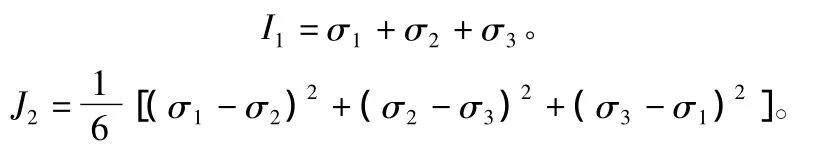
其中，α，k分別為與巖土材料粘聚力c和內摩擦角φ有關的常數;Ⅰ1為應力張量的第一不變量;J2為應力偏張量的第二不變量;σ1，σ2，σ3均為主應力。

采用有限元強度折減法計算時，首先選取初始折減系數Fi，然后對邊坡土體材料強度系數進行折減，并進行有限元計算，若程序收斂，說明土體仍處于穩定狀態;繼續增大折減系數Fi，直到有限元計算發散，此時對應的折減系數F1即為穩定或安全系數。

在極限平衡法中，若假定某剪切面土體的正應力和剪應力分別為σ和τ，采用Mohr-Coulomb屈服準則，抗剪強度為:τf=c+σtanφ。安全系數定義為沿剪切面的抗剪強度與剪切面上實際剪力的比值，即:假設該狀態時土體尚未發生破壞，其實際剪應力與實際得以發揮的抗剪強度相同，即有:據此可得折減后的抗剪強度指標分別為:

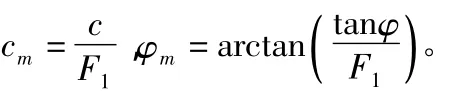
由此可看出，有限元強度折減法與極限平衡法在本質上是一致的。

1.2 數值模型和邊界條件

取某高速公路K37+325右側為分析對象。邊坡為四級:一級邊坡為 1∶0.75，坡高 10m;二、三級邊坡均為 1∶1，坡高均為 10m;四級邊坡為1∶1.25，坡高為7m;每級邊坡均設2m寬平臺。地質勘探表明，坡體均為風化泥灰巖，工程特性為:容重γ=25 kN/m3，彈性模量 E=2.55 GPa，泊松比 v=0.27，粘聚力 c=200 kPa，內摩擦角φ=35°。計算模型簡化為平面應變問題。有限元建模時，巖體用Plane82單元模擬，邊坡向下延伸35m，左側向公路延伸30m，右側向后延伸40m。取為雙層模型，模型最下部15m范圍內為彈性材料，其余部分取為理想彈塑性材料。邊界條件為:邊坡左右兩側約束水平位移，底部約束豎向和水平位移，上部為自由邊界。有限元模型采用映射網格，共劃分單元3 399個，節點10 468個。

有限元模型如圖1所示。

圖1 有限元模型

2 計算結果分析

對有限元模型施加Y方向的重力加速度，采用強度折減法依次進行邊坡穩定性的計算。圖2～圖5給出了不同F值時邊坡的塑性區。由圖2～圖5可以看出，隨著粘聚力c和內摩擦角φ的折減，邊坡的塑性區域不斷向上發展，直至形成一個貫通的滑面，邊坡將沿此滑面滑移破壞。當F=3.46時，邊坡的滑移面形成，且此時有限元計算不收斂，所以此時的折減系數即為邊坡的穩定安全系數，即該邊坡的穩定安全系數為F1=3.46。

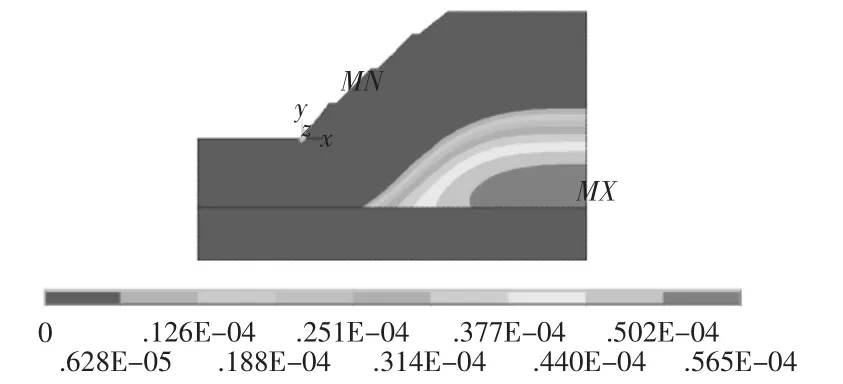
圖2 F=2.0時塑性區域云圖

3 邊坡穩定性評價

根據有限元計算可確定邊坡滑移面各控制點的坐標，可繪制邊坡及其滑移面的位置和形狀。再按照傳統極限平衡法Bishop法計算得到安全系數為3.098。

根據上述計算結果，考慮外荷載等因素可確定該邊坡是穩定的。

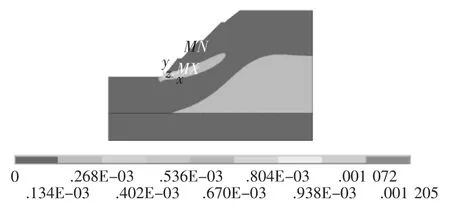
圖3 F=3.3時塑性區域云圖

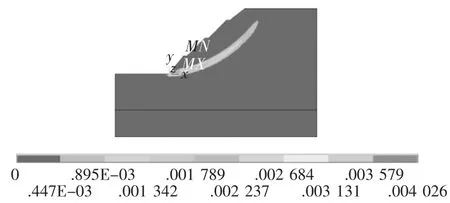
圖4 F=3.46時塑性區域云圖

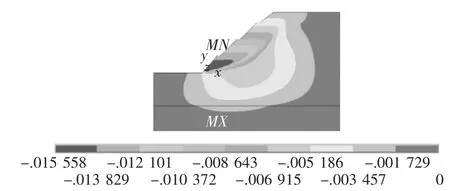
圖5 F=3.46時X方向位移圖

4 結語

1)采用有限元軟件對邊坡進行穩定性分析，可以反映邊坡的變形大小、塑性區域分布以及擴展過程，并能確定滑移面的位置和形狀。與傳統極限平衡法比較，有限元法更為直觀，精度也能滿足工程要求，用該法分析邊坡穩定性是合理可行的。

2)邊坡的滑移面與邊坡坡角、粘聚力和內摩擦角等因素有關，滑移面的形成總伴隨著塑性變形的發生和塑性區域的開展，塑性區域發展至坡頂時，表明滑移面已貫通，邊坡失穩破壞。

3)計算所得邊坡安全系數較低，即邊坡穩定性不夠時，可通過預應力錨索加固以提高坡體的整體穩定性。

[1]鄭穎人，龔曉南.巖土塑性力學基礎[M］.北京:中國建筑工業出版社，1989.

[2]李宇峙.公路工程概論[M］.北京:人民交通出版社，1995.

[3]夏元友，李 梅.邊坡穩定性評價方法研究及發展趨勢[J］.巖石力學與工程學報，2002，21(7):1087-1091.

[4]鄭穎人，趙尚毅.有限元強度折減法在土坡與巖坡中的應用[J］.巖石力學與工程學報，2004，23(19):3381-3388.

[5]趙尚毅，鄭穎人，時衛民，等.用有限元強度折減法求邊坡穩定安全系數[J］.巖土工程學報，2002，24(3):343-346.

[6]熊保林，王希良，路春嬌.山區高速公路高陡邊坡三維有限元分析[J］.中外公路，2010，8(4):70-72.

[7]李晶巖，付 麗.邊坡穩定性分析方法[J］.山西建筑，2011，37(4):65-66.