基于反饋機制的自愈算法

趙季紅 ，曲樺，陳文東

(1. 西安交通大學 電子與信息工程學院，陜西 西安 710049;

2. 西安郵電學院 通信與信息工程學院，陜西 西安 710061)

1 引言

隨著通信網絡寬帶化進程的逐步深入，業務類型的日漸豐富，網絡的生存性問題成為研究的熱點。故障恢復是網絡生存性研究的重要組成部分[1,2]，而自愈作為一種智能化的故障恢復技術，其研究也成為了一種趨勢。

自愈通常是指網絡在發生故障的情況下，不需要人工干預，能很快地、自發地恢復受影響的業務[3]。這就要求網絡設備具備更強的計算和存儲能力。自愈的基本原理是在節點檢測到故障之后，立即通知源節點重新選擇一條路徑，即在邊緣節點之間建立另外一條能夠滿足業務傳輸需求的路徑，將受影響的流量切換到這條備份路徑上去，從而保證業務的連續傳輸。

自愈的研究現狀主要集中于2個方面：故障檢測和故障恢復。故障檢測旨在感知并且定位網絡故障[4]。當網絡中檢測到故障之后，故障恢復機制開始運作。故障恢復旨在將故障路徑上的流量切換到另一條可承載這些流量的健康路徑上，減少由于故障對業務傳輸所造成的影響。

目前故障檢測主要有 RSVP軟狀態、RSVP HELLO、LSP PING/Traceroute[5]以及 BFD[6]等技術。這幾種技術所花費的檢測時間較長，意味著在故障發生到故障被檢測期間，將有大量的數據丟失。故障恢復的研究主要集中于2種機制：保護交換和重路由。保護交換的前提是為可能的故障路徑提前找到一條備份路徑。當故障發生后，將流量切換到備份路徑上保證業務的傳輸。這種機制的主要問題是備份路徑會占用大量的網絡資源，造成資源的利用率偏低[7]。重路由主要有2個思路，靜態路由和在線路由。靜態路由將網絡在很長一段時間的平均流量作為網絡的當前流量信息，在這個基礎上計算路由。這種方法簡單卻精度較差。目前，靜態路由主要有最寬最短路徑（WSP）算法[8]、最大可預留帶寬（MRB）算法[9]。在線路由則基于當前網絡的狀態信息，計算并選擇最小可能出現擁塞的路徑傳輸業務，網絡狀態信息更新的即時性和準確性很大程度上決定了算法的性能。目前，在線路由主要包括最小沖突路由算法（MIRA）[10]、動態在線路由算法（DORA）[11]、最小沖突優化算法（LIOA）[12]等。重路由對于新路徑的建立依賴于故障信息、網絡路由的策略、預定義設置以及網絡當前的狀態信息，利用這些信息的路由算法，其收斂時間得不到保證，導致故障恢復時間不能滿足業務的QoS傳輸。

根據上述分析，自愈技術的研究仍有許多問題亟待解決。第一，自愈以故障檢測為前提，對故障檢測結果的依賴程度過高。首先，自愈算法的觸發是在故障檢測之后進行的，當網絡發生故障后，只有該故障被感知并且被定位之后才能觸發自愈算法，因此自愈算法需要等待故障檢測所需的時間。其次，如果故障未被成功檢測，那么自愈算法就不能被觸發，從而導致故障恢復失敗。第二，自愈進行重路由計算的時間過長，其收斂的時間很難符合業務傳輸質量的要求。而且基于QoS約束重路由計算需要隨時掌握當前網絡狀態信息，這些信息的收集往往通過泛洪的方式，會造成一定的資源浪費。

針對上述問題，本文提出了一種基于反饋機制的自愈算法。該算法通過引入Q學習的反饋機制，可以感知網絡當前的狀態信息，也可以感知到路徑發生故障或者擁塞的情況，這樣大大降低了自愈對于故障檢測的依賴程度，不必對故障進行精確地定位，只需要模糊的感知故障或擁塞，自愈就可以啟動。另一方面，該算法可以通過業務的傳輸收集路徑的信息（時延、帶寬等），通過對這些信息的學習，可以獲得學習“經驗”并作為重路由選擇的依據，避免了繁雜的重路由計算過程，降低了重路由所需的時間。同時，該算法引入了多 QoS參數約束評價函數的路由計算以及Boltzmann-Gibbs分布的路徑選擇策略，使算法具備了區分業務能力以及網絡資源優化能力。

本文首先介紹了算法設計中的幾個基本概念，然后詳細介紹了算法應用于網絡中的網絡模型、算法的數學模型以及算法實現的具體流程和步驟。最后，用 MATLAB對該算法進行了仿真，并對算法的性能進行了討論。

2 算法設計中的基本概念

2.1 反饋機制

本文的研究旨在通過引入機器學習理論改善目前傳統自愈機制缺乏對于網絡環境的學習能力的狀況，提高自愈機制的智能性。機器學習理論中的學習策略很多，比如類比學習、歸納學習、支持向量機和強化學習等，其中強化學習源于心理學中的“試錯法”，通過不斷與環境交互來改善策略最終找到適合環境的最優策略，這種與環境交互的思想可以應用到網絡中實現對網絡環境的學習。

本文中提出的算法通過引入強化學習理論中的Q學習[13]反饋機制來感知網絡當前狀態的變化，一定程度上緩解了傳統自愈機制對于故障檢測技術依賴程度過高的問題。同時，利用反饋機制可以降低在線路由計算中由于泛洪流量對網絡資源的浪費。反饋機制原理如圖1所示。

圖1 基于Q學習的反饋機制

圖1 中，當每個業務傳輸結束的時候，目的節點Egress會將該業務傳輸路徑的狀態信息反饋給源節點Ingress。Ingress通過這個反饋回來的狀態信息感知該路徑的承載能力。反饋回來的狀態信息本質上是業務傳輸完成后學習到的“經驗”。這樣就可以避免每次重路由時重新計算新的路徑，而是直接利用先前的“經驗”自適應地選擇合適的備份路徑，從路由重計算到路由重查表，可以大大節省不必要的計算負擔。

考慮到可以人為定義反映網絡狀態信息的評價函數，那么可以把其定義為一個數值。這樣反饋流量占用的帶寬和傳輸產生的時延可以忽略不記。因此，這種反饋機制較傳統的泛洪廣播網絡狀態信息的方式更加簡單，而且能夠有效減少網絡中不必要的泛洪流量。

綜上所述，通過反饋機制，Ingress節點依靠感知當前網絡狀態并且積累學習“經驗”來選擇路徑，在很大程度上降低自愈機制對故障檢測的依賴程度，同時提高了網絡資源利用率。

2.2 業務分類

網絡中的有些業務對實時性的要求較高，必須滿足其實時傳輸，才能保證業務的服務質量（QoS）；而有些業務對網絡的吞吐量和分組丟失率的要求較高，只有足夠大的吞吐量和足夠低的分組丟失率才能保證業務的服務質量；還有一些業務對網絡的要求不高，采用傳統“盡力而為”服務即可，這類業務應該盡量少地占用網絡資源。

為了合理地利用有限的網絡資源，本文提出的算法的路由策略會依據不同業務類型選擇適合其傳輸需求的最優路徑。在本文中，將業務分成3種類型：EF業務、AF業務和BE業務。EF業務為加速轉發業務，AF業務為確保轉發業務，BE業務為盡力而為轉發業務。3種業務對于QoS參數的要求參見表1。

表1 不同業務類型對QoS參數的要求

2.3 多QoS約束評價函數

一些自愈技術在尋找備份路徑進行故障恢復的時候只考慮單一因素的約束，這樣帶來的問題是選擇的路徑不一定能夠充分地滿足業務傳輸的QoS需求，因為保證業務QoS傳輸需要考慮的參數很多，只滿足其中一個不一定能達到傳輸的要求。因此，本文提出的算法引入多QoS參數的約束，這樣反饋的評價函數所包含的網絡狀態信息會更加全面。

本文中，選取3種常用的QoS參數作為約束集合：吞吐量（TH）、端到端時延（delay）和分組丟失率（P）。這些參數都體現的是路徑端到端的性能，綜合考慮這些約束因素選擇出來的路徑就會融入這些約束信息，使路徑的選擇更加科學和可靠，更能滿足業務的QoS傳輸需求。很明顯，EF、AF業務的優先級和重要性要遠遠高于BE業務，因此希望 BE業務盡量少地占用網絡中的節點和鏈路資源。使用U表示路徑對網絡節點和鏈路資源的利用率，U=Npath/ Nall，其中，Npath表示一條路徑使用的節點數，Nall表示網絡中節點個數總和。那么，約束集合C={TH, delay, P, U}。

評價函數為約束集合C的函數，即f(C)。評價函數的大小就體現了網絡中路徑的端到端的承載能力的好壞。其值越大，說明該路徑當前的承載能力越強。

2.4 資源優化

靜態路由算法通常會使業務集中于一條基于某種準則的“最優”路徑。當網絡中負載較大時，會產生路徑擁塞，這就需要全局服務器對流量進行控制來解決這一問題。在本文中，源節點 Ingress可以得到評價函數提供的信息，因此可以感知到網絡當前各條路徑的負載情況，從而避免選擇負載較大的路徑進行業務的傳輸。但網絡中的負載情況是隨著時間變化而變化的，這就需要算法對網絡狀態信息的動態感知。本文中，源節點具有動態感知網絡狀態信息的能力，從而能夠依據路徑選擇策略自適應地選擇路徑，使網絡負載均衡，實現網絡資源的優化。

3 基于反饋機制的自愈算法

基于反饋機制的自愈算法以強化學習中的 Q學習算法作為理論基礎，應用于網絡中以增強自愈機制的學習能力，提高自愈機制對于網絡環境的感知力，實現網絡的智能化控制。

3.1 數學模型

本文中反饋機制的實現是基于強化學習理論中的Q學習算法。Q學習就是要在系統動力學特性未知的情況下估計最優策略的Q值，詳見文獻[13]。在線Q學習方法的實現是按遞歸公式(3)進行的：在每個時間步 t，觀察當前狀態 St，選擇和執行動作At，再觀察后續狀態 St+1并接受立即回報Rt，然后根據式(3)來調整Q值。

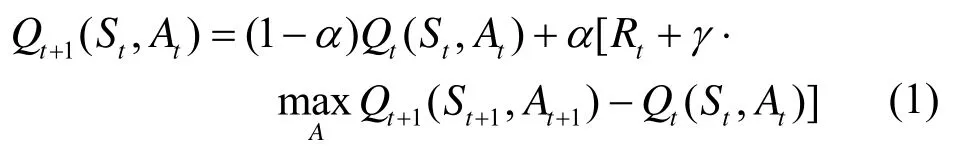
式(1)中，α為學習率，它控制著學習的速度，α越大則收斂越快。但是過大的α可能導致不收斂。Watkins證明了α在滿足一定條件時，如果任一個二元組(St,At)能用方程(1)進行無窮多次迭代，則當 t趨于無窮時，Qt(St,At)以概率1收斂到關于最優策略的Q*(St,At)[13]。

根據多 QoS參數約束的需要，定義立即回報Reward為多 QoS約束的評價函數以滿足業務的QoS需求。從上文可知，Reward是約束集C的函數。令 R={R1, R2, … , Rm}表示每個行動對應的Reward的集合。定義

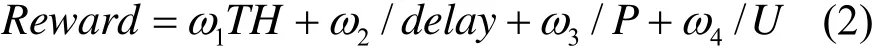
式(2)中ω1、ω2、ω3和ω4為權系數。調整權系數的大小可以體現出不同類型業務（EF業務、AF業務和BE業務）的需求。

Q學習算法中， Agent面臨的一個問題是如果選擇下一個動作，通常需要考慮2方面的因素。其一是Agent必須對狀態動作空間做充分的探索從而能夠找出最優或近最優的策略。另一方面是利用通過學習已獲得的經驗進行動作選擇，從而使學習的成本降低。可以采用連續可微且近似貪婪的Boltzmann-Gibbs分布[14]作為動作選取策略，動作Ak被選取的概率為

式(3)中，Tt(＞0)為溫度參數，控制行為選取的隨機程度。為了提高學習的速度，利用模擬退火技術在學習過程中按式(4)進行動態調整溫度值，即在學習的初期選擇較大的溫度，以保證動作選取的隨機性較大，增加搜索能力，然后在學習的過程中逐漸降低溫度，保證以前的學習效果不被破壞[14]。

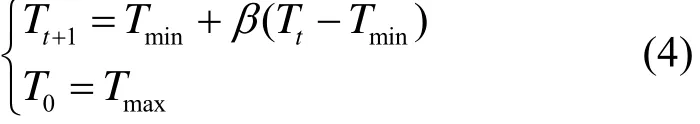
式(4)中, β 為退火因子，并且 0＜β ＜1。

3.2 網絡模型

本文提出的基于反饋機制的自愈算法可以應用在任何Mesh網絡中。本文將以MPLS網絡作為應用場景對算法的實現進行詳細地研究。

將MPLS網絡的拓撲抽象為G(V,E)，V代表網絡中的節點（路由器），E代表網絡中的鏈路。令S={S1, S2,… , Sn}表示MPLS網絡環境中的邊緣節點的集合（邊緣路由器LER或者自治域范圍內的邊緣標簽交換路由器LSR），Si∈V。假設S1為業務傳輸源節點，那么選擇S1作為Q學習Agent，潛在的目的節點集合S’={S2, … , Sn}即作為Q學習中的環境狀態集，顯然S’為有限集。源節點與目的節點之間所有可能的傳輸路徑集合為 A={A1, A2, … ,Am}，A即為Q學習Agent可以采取的行動集合，即是MPLS網絡的標簽交換路徑（LSP）。Agent每采取一次行動，即每選擇一條路徑，都會產生一個與這次行動相對應的回報 Reward（式（2））反饋給源節點，然后根據式(1)更新此次業務傳輸之后對應路徑的Qt(Si,Aj) 值，Si表示業務傳輸的目的節點；Aj表示業務到達Si的傳輸路徑。網絡模型如圖2所示。

圖2 Q學習在MPLS網絡中的應用模型

Qt(Si,Aj)值大小決定了選擇路徑 Aj到目標節點 Si的“傾向”。將所有 Q值建立起來的矩陣Qt(Si,Aj)（i∈[1,n]，j∈[1,m]） 定義為 Q 表格，表示業務的路由信息。S1節點中儲存的Q表格如表2所示。

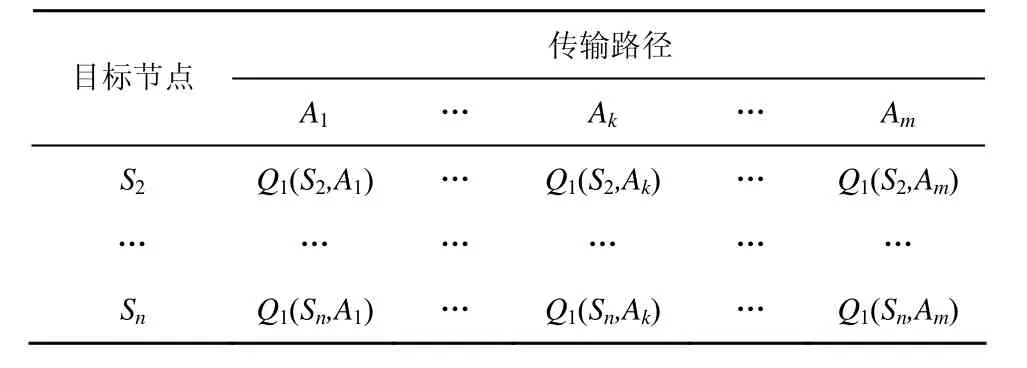
表2 Q表格

當業務傳輸結束并反饋Reward更新Q表格信息之后，就可以以式(3)作為路徑選取策略來選擇新業務的傳輸路徑，更新后的 Q表格融入了反饋信息，因此具備網絡狀態的感知能力，同樣也具備了故障的感知能力。

3.3 算法流程

算法的實現流程如圖3所示。

具體實現步驟如下。

step1 當業務從源節點接入后，判斷業務的類型。

step2 源節點根據業務的類型查詢相應的路徑優先級表格（EF業務Q表格、AF業務Q表格和BE業務Q表格）。

step3 依據基于Boltzmann-Gibbs分布的路徑選擇策略（式(3)）得到業務的傳輸路徑Ai。

step4 在業務傳輸過程中經過鏈路時，記錄鏈路的吞吐量和時延信息。

step5 在業務到達目的節點后，將所得到的路徑信息進行整合，計算出路徑吞吐量、路徑時延以及業務數據的分組丟失率，根據式(2)計算得到此次業務傳輸的Reward，并反饋給源節點。

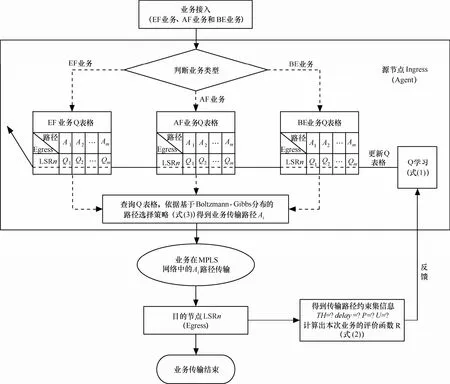
圖3 算法的實現流程

step6 利用 Q 學習算法（式（1））得到更新后的Q值，從而對路徑的優先級信息進行更新。新業務到來時便查詢更新后的相應業務的Q表格，重復如上的步驟找到傳輸路徑。

在本文中，業務的傳輸需要考慮2種情況，一種是業務傳輸成功的情況，一種是業務傳輸失敗的情況。在第1種情況下，對算法收斂速度的要求不能過高，因為過快地收斂可能導致較大的擾動，學習的精確性不能得到很好地保證。在第2種情況下，業務傳輸失敗很可能是由于鏈路或者節點出現故障造成的，對于這種情況，希望算法能對其進行較快地學習，因此希望收斂速度快。這2種情況可以通過使用不同的學習率α實現。算法可用下面的偽代碼表示。

算法1 基于反饋機制的自愈算法

對于任意源節點Si∈S；

初始化 Qi(Sj,Ak)，其中，Sj為目的節點，Ak為選擇的路徑，在所有 Ak中，取最少跳數路徑的Qi(Sj,Ak)為1，其余值為0；

根據式(3)的隨機分布選擇路徑，假設選擇路徑Am；

根據式(2)，計算相應的Reward函數；

如果業務傳輸成功，依據下式更新Q表格：

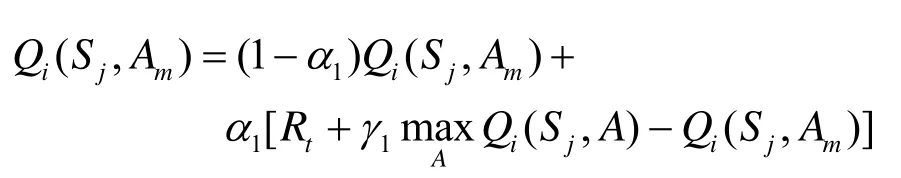
如果業務傳輸失敗，依據下式更新Q表格：

4 仿真與性能分析

本節將對算法進行仿真并依據仿真結果分析算法各方面的性能。需要特別說明的是本文提出的算法改變了傳統的自愈機制的以故障檢測為前提的故障恢復模式，而是利用Q學習反饋機制的故障感知能力先于定位故障提前響應故障，因此缺少同類的自愈機制進行比較。在仿真中，將采用無反饋的靜態自愈機制說明基于反饋的自愈機制對于網絡環境的學習能力的改善。

4.1 網絡參數設置

仿真中的網絡拓撲如圖 4所示。其中，LSR1為源節點，同時也是Q學習Agent。LSR15為目的節點，Reward將從這個節點反饋到LSR1以更新Q表格。

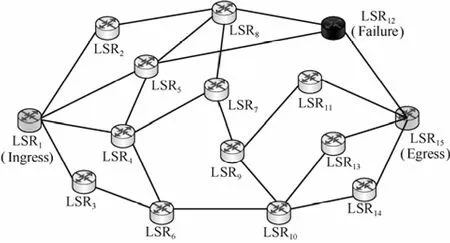
圖4 網絡拓撲（LSR12為故障場景中的故障節點）

LSR1和LSR15之間有22條可用傳輸路徑，路徑信息參見表 3。其中，對路徑的約束參數包括路徑吞吐量（Mbit/s）、路徑時延（ms）和路徑節點數。在仿真中，路徑的分組丟失率與路徑剩余帶寬之間呈指數關系。

表3 仿真參數設置

表3中，靜態路徑選擇指的是靜態路由算法中3種業務可以選擇的路徑。EF業務選擇的路徑為1、2、4、5、12、20、21和 22；AF業務選擇的路徑為 1、3、7、10、11、17、20、21和 22；BE 業務可以選擇所有路徑。靜態算法沒有引入反饋機制，作為與本文提出算法的對比算法。

在仿真中，設置LSR12為可能發生故障的節點。從表3中可以看出，如果LSR12發生故障，受影響的路徑有1、5、9、13、18和19。仿真中還加入了鏈路擁塞的情況，為了便于觀察，設置路徑22為可能發生擁塞的路徑。因此，仿真中包括3種場景，分別為無故障場景、LSR12故障場景和路徑22擁塞場景。

在仿真中，需要在網絡負載大小變化條件下討論算法性能，因此，對網絡負載定義如下 10個等級，如表4所示。等級越高，表明網絡負載越大。

表4 負載級別定義

4.2 性能分析

4.2.1 故障感知

本文中提出的算法通過業務傳輸之后評價函數的反饋機制感知網絡當前的狀態信息。因此，該算法具備故障感知的能力。令

φ 越小說明算法感知故障的能力越強；反之，算法感知故障的能力就越弱。仿真結果如圖5所示。圖5(b)反映了本文提出的算法對故障感知的性能，圖5(a)反映了沒有加入反饋機制的靜態路由算法對故障感知的性能。從仿真結果可以看出，基于反饋機制的算法在故障感知性能上表現出了一定的優勢。

圖5 故障感知性能

4.2.2 故障恢復

在本文算法的自愈機制中，如果EF業務或者AF業務傳輸失敗時，即選擇了故障路徑時，源節點會重新選擇路徑傳輸業務。如果重新選擇的路徑不能滿足業務傳輸的QoS或者仍然選擇了故障路徑，則認為業務恢復失敗，即沒有找到合適的備份路徑保證業務的傳輸；如果重新選擇的路徑可以滿足業務的 QoS，并且不是故障路徑，則認為業務恢復成功，即找到了一條合適的備份路徑保證業務的傳輸。因此，業務恢復失敗率可以表示為

仿真結果如圖6所示。

圖6 故障恢復性能

4.2.3 區分業務

圖7從業務平均時延、路徑平均剩余帶寬和業務平均分組丟失率 3個方面說明了算法對于 EF、AF和BE業務的區分能力。

從圖 7(a)中可以明顯看出，EF業務的平均時延最小，AF業務次之，BE業務最大。這說明，算法對于EF業務，更傾向于選擇時延小的路徑保證業務的實時傳輸，而AF業務和BE業務的時延保證則相對較差。從圖 7(b)中可以明顯看出，AF業務選擇路徑的平均剩余帶寬最大，EF業務次之，BE業務最小。算法對于AF業務，更傾向于選擇吞吐量大的路徑保證業務的傳輸，而對EF業務和BE業務，則這方面的保證相對較差。從圖7(c)中可以明顯看出，AF業務的平均分組丟失率最小，EF業務次之，BE業務最大。這說明，算法對于AF業務和EF業務，更傾向于選擇分組丟失率小的路徑保證業務的傳輸，而對BE業務的分組丟失率保證相對較差。

圖7 區分業務性能

圖7 的結果說明算法對EF、AF和BE 3種業務進行了區分服務，在有限的網絡資源條件下，滿足了EF業務和AF業務的傳輸需求。

4.2.4 網絡資源優化

本文提出的算法通過反饋機制可以感知路徑的剩余帶寬，在源節點選擇路徑時，會根據剩余帶寬情況動態進行路徑的分配。因此，網絡中流量會比較均衡。而靜態路由算法由于沒有引入反饋機制，缺少對路徑剩余帶寬的感知能力，因此在選路時，不會考慮到網絡的負載情況，只根據靜態路由表進行路由。因此，各路徑的負載情況不一定會均衡，網絡資源利用率偏低。將圖8(a)和圖8(b)進行比較，可以明顯看出，基于反饋機制的自愈算法可以使網絡中各路徑的負載均衡化，具有網絡資源優化的能力，在圖中顯示的效果是路徑剩余帶寬平面比較平滑，而靜態路由算法中的路徑剩余帶寬平面就顯得凹凸不平。

圖8 資源優化性能

4.2.5 學習率α1、α2對算法性能的影響

在本文中，α1為業務傳輸成功時的學習率，α2為業務傳輸失敗時的學習率。學習率越大，則算法收斂速度越快，但抖動也越大，而且如果學習率過大，還有可能導致算法不收斂。分別選取AF業務在故障路徑17和擁塞路徑22上的Q值變化曲線說明學習率對算法性能的影響，如圖 9所示。

圖9 學習率α1、α2對算法性能的影響

在仿真進行到1/4時，故障發生，路徑17中斷，所以此時影響算法收斂速度的學習率為α2；當仿真進行到3/4時，故障結束，路徑17恢復，所以影響算法收斂速度的學習率變為α1。從圖9(a)中可以看出，在故障發生時，當學習率較大時，收斂速度較快，但有一定的抖動。從圖9(b)中可以看出，在擁塞發生的時候，較大的α1對應曲線的收斂速度較快，但抖動較大。

5 結束語

本文提出了一種基于反饋機制的自愈算法。利用Q學習的反饋機制，降低了傳統自愈機制對故障檢測的依賴程度，在一定程度上提高了算法對于故障感知的靈敏度，從而提高了故障恢復率。算法利用多QoS約束的評價函數，對于不同類型業務查詢不同的Q表格從而使其具備區分業務的能力，同時，通過對網絡狀態信息的反饋以及基于Boltzmann-Gibbs分布的路徑選擇策略也在一定程度提高了網絡資源的利用率，達到了網絡資源優化的目的。

[1] IETF RFC 3469. Framework for Multi-Protocol Label Switching(MPLS)-based Recovery[S]. 2003.

[2] JORGE L, GOMES T. Survey of recovery schemes in MPLS networks[A]. 2006 International Conference on Dependability of Computer Systems[C]. Szklarska Poreba, Poland, 2006.

[3] YIJUN X, MASON L G. Restoration strategies and spare capacity requirements in self-healing ATM networks[J]. IEEE/ACM Transactions on Networking, 1999, 7(1): 98-110.

[4] CAVENDISH D, OHTA H, RAKOTORANTO H. Operation, administration, and maintenance in MPLS Networks[A]. IEEE Communications Magazine[C]. 2004. 91-99.

[5] IETF RFC 4379. Detecting Multi-protocol Label Switched (MPLS)Data Plane Failures[S]. 2006.

[6] IETF DRAFT. Bidirectional Fowarding Detection[S]. 2007.

[7] IETF RFC 3469. Framework for Multi-Protocol Label Switching(MPLS)-based Recovery[S]. 2003.

[8] GRERIN R, WILLIAMS D, ORDA A. QoS routing mechanisms and OSPF extensions[A]. 1997 Global Telecommunications Conference[C].Phoenix, 1997.

[9] KE Y, COPELAND G A. Scalability of routing advertisement for QoS routing in an IP network with guaranteed QoS[A]. 2000 Global Telecommunications Conference[C]. San Francisco, 2000.

[10] KODIALAM M, LAKSHMAN T. Minimum interference routing with applications to MPLS traffic engineering[A]. Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies[C].Tel Aviv, 2000.

[11] SZETO W, BOUTABA R, IRAQI Y, Dynamic online routing algorithm for MPLS traffic engineering[A]. The 9th International Conference on Advanced Communication Technology[C]. Gangwon-Do,Korea, 2007.

[12] BAGULA B, BOTHA M, KRZESINSKI A. Online traffic engineering:the least interference optimization algorithm[A]. 2004 IEEE International Conference on Communications[C]. Paris, France, 2004.

[13] KAELBLING L P, LITTMAN M L, MOORE A W. Reinforcement learning: a survey[J]. Journal of Artificial Intelligence Research, 1996,4(1): 237-285.

[14] SUTTON R S, BARTO A G. Reinforcement Learning: An Introduction[M]. The MIT Press, Cambridge, MA, 1998.