非對稱雙向中繼系統中的協作多址廣播傳輸方案設計與數據率性能分析

吳丹，田亞飛，楊晨陽

(北京航空航天大學 電子信息工程學院，北京 100191)

1 引言

中繼技術可以有效地擴展無線通信系統的覆蓋范圍或者提升用戶的吞吐量[1]。在傳統的半雙工中繼系統中，完成源節點與目的節點間的雙向信息交換需要4個時隙。為了恢復半雙工中繼帶來的頻譜效率損失，最近人們提出了雙向中繼技術[2~5]，只需要2個時隙即可以完成雙邊信息交換。在雙向中繼系統中，根據中繼處理方式不同，可以采用放大轉發（AF, amplify-and-forward）[6]、解碼轉發（DF,decode-and-forward）[7]、估計轉發（EF, estimate-and-forward）[8]或降噪轉發（DnF, denoise-and-forward）[9]等多種中繼轉發方式。

單用戶雙向中繼系統由基站a、用戶b以及一個中繼節點r組成，2個節點a、b通過中繼交換信息。雙向中繼中2種最基本的傳輸方案為2時隙多址廣播（MABC, multiple access broadcast）和3時隙時分廣播（TDBC, time division broadcast）。在MABC方案中，第1個階段為多址階段，2個發射節點同時向中繼發射信號，而第2個時隙為廣播階段，中繼向 2個節點廣播數據。研究表明，采用MABC方案的雙向中繼系統的和數據率是單向中繼系統的2倍[10]。在TDBC方案中，在前2個時隙節點a和節點b分別向中繼發射數據，中繼在第3個時隙進行廣播。與傳統的4時隙方案比較，當中繼處的2路接收信號信噪比相差不大時，TDBC可以將系統吞吐量提高1/3[11]。文獻 [12] 分析并比較了這2種傳輸方案的容量上界和可達數據率域，結果表明MABC方案的上界始終高于TDBC方案，但在非對稱信道中，MABC的可達和數據率較低。

在非對稱雙向中繼信道中，2個源節點與中繼間的信道質量不同，一端節點與中繼間的信道容量較高，此時，已有的雙向中繼方案不能充分利用信道資源。若節點a與中繼r間的信道（ar→鏈路）質量較好，在 MABC方案中，中繼以較高的速率接收節點a的數據，而只能以較低的速率轉發；而節點b正好相反，它發送的數據以較低的速率到達中繼，而以較高速率被轉發。當節點a已經成功接收完節點b的數據后，中繼處還有大量數據需要轉發至節點b。如果中繼節點繼續發射，則節點a轉入空閑狀態。在TDBC方案中，雖然可以通過控制前2個時隙的長度保證中繼在第3個時隙恰好廣播完雙向數據，從而沒有空閑時隙，但是這使得節點b在第2個時隙需要傳輸較長時間，導致系統和數據率依然較低。可以看出，在非對稱信道雙向中繼系統中，較差的鏈路限制了雙向傳輸的數據率，對系統性能影響很大。

在實際系統中，如蜂窩網絡，由于中繼位置以及信道衰落造成的信道非對稱情況十分常見。另一方面，由于服務質量需求的不同，對上下行數據率的要求往往也不一樣。例如，語音或視頻業務對上下行數據率要求幾乎相等；下載業務對下行數據率要求較高；某些網絡游戲則需要較低的上行傳輸時延。在這些情況下，加權和數據率能更準確地反映系統性能。

目前針對非對稱信道或非對稱數據率的解決方案并不多。在文獻[13]中，作者針對MABC方案的廣播階段，設計了采用DF中繼時非對稱數據率的傳輸方案，但沒有聯合考慮多址階段的傳輸方案。在文獻[14]中，作者針對 MABC方案設計了CF中繼、非對稱數據率傳輸的碼本。在文獻[15]中，作者對信號采用分層調制方式以適應非對稱信道的傳輸特點，從而降低TDBC方案下的誤比特率。這些方案縮短了可達和數據率與容量上界之間的差距，但并未提高容量上界本身。

本文提出一種非對稱雙向中繼傳輸方案，稱為協作多址廣播方案（CoMABC, cooperative multiple access broadcast）。此方案在采用2時隙MABC方案進行傳輸后，引入第3個時隙，使得中繼與空閑節點協作向另一節點傳輸。本文將研究新方案的容量上界以及DF方式下的可達數據率域，給出系統在加性白高斯噪聲信道（AWGN）以及瑞利衰落信道下的性能。為了得到最大加權和數據率，將對時隙以及功率進行優化。分析結果表明，CoMABC方案能夠提高非對稱信道下系統的加權和容量與加權和數據率。

本文章節安排如下：第2節給出系統模型；在第3節中，提出新的傳輸方案，并推導新方案的容量上界以及可達速率域，對資源優化優化問題進行建模；仿真結果與分析在第4節中給出，最后是結束語。

2 系統模型

考慮最基本的單天線3節點雙向中繼系統，其中基站 （用節點a表示）和用戶（用節點b表示）通過一個時分雙工（TDD）中繼（用節點r表示）相互通信。傳輸過程在單位時間內完成，共有M個時隙，用tm表示第m個時隙，因此

用hij表示節點i與節點 j間的信道，其中，i, j=a,b, r。在TDD系統中，假設上下行信道具有理想互異性，故hij= hji。在AWGN信道下，考慮由路徑損耗所帶來的信道非對稱性的影響；而在瑞利衰落信道下，信道非對稱性不僅與路徑損耗有關，也與小尺度衰落有關。

s(m)為節點i在第m個時隙發射的比特信息，i經調制后以Rij的速率發射至節點j。調制后的數據為x(m)=M(m)（s(m)）。由于不同鏈路的信道條件不i,ji,ji同，為了充分利用信道資源，對發射信號采用不同的調制和編碼方式，這里 Mi

(,mj

)表示第 m個時隙節點i發射至節點j的數據所采用的調制方式。調制后的信號滿足能量約束E（x2）= 1。3個節點a、b、i,jr處的發射功率分別為Pa、Pb以及Pr。因此，接收機j處的接收信號可以表示為

其中，nj為零均值單位方差加性復高斯白噪聲。

3 系統傳輸方案及性能分析

本節針對MABC和TDBC方案在非對稱信道下不能充分利用信道資源的問題，設計一種新的3時隙協作多址廣播傳輸方案，并給出采用DF中繼時的可實現方案。而后，將推導所提出方案的容量上界及DF方式下的可達數據率域，并對達到加權和數據率上界及可達加權和數據率的資源優化問題進行建模。

3.1 系統傳輸方案

在下面的分析中，假設節點a與中繼r間的信道質量優于節點b與中繼間的信道。當br?鏈路質量較好時，只需在下面的步驟中將節點a與節點b互換即可。

CoMABC方案考慮在MABC方案中引入第3個時隙，使得空閑節點a可以與中繼節點協作發射，從而提高非對稱信道下的系統性能。傳輸過程如圖1所示。

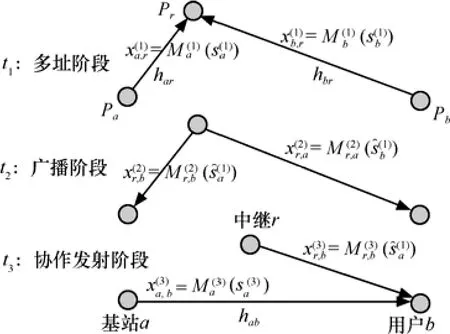
圖1 協作多址廣播（CoMABC）傳輸方案

下面提出中繼 DF轉發模式下的一種可實現傳輸方案。

第1個時隙t1為多址階段，2節點a、b同時向中 繼 發 射 調 制 后 的 數 據 x(1)=M(1)（s(1)）和a,raax(1)= M(1)（ s(1)）。中繼端的接收信號為b,rbb

當中繼兩端信道不對稱時，a、b節點發射的數據在中繼處的接收信噪比相差較大。在DF模式下，中繼端進行串行干擾消除，從而可以分別得到2路信號的估計值 s?a(1)和s?b(1)。

第2個時隙t2為廣播階段，為了適應廣播信道，中繼需要對2路信號重新調制后進行功率分配，并以模擬網絡編碼[9]的方式合并后廣播。設β為功率分配因子，為r→b鏈路分配的發射功率為βPr，而為r→a鏈路分配的發射功率為(1-β)Pr。因此，t2時隙中繼發射信號為

節點a和b分別接收到2路數據的和信號：

其中，j=a, b。

a、b節點均已知各自的發射數據sa和sb，因此在刪除自己發射數據產生的接收信號（即自干擾信號）后，可以得到對方節點的信息。

在非對稱信道下，在t2時隙結束時，中繼無法完全轉發節點a的數據。在第3個時隙t3，由中繼和節點a同時向節點b發射數據。中繼負責轉發在上一個時隙未能成功轉發的數據，而節點a繼續發送后續數據。在t3結束時，節點b的接收信號為

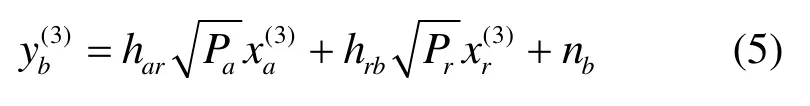
接收端對2路數據進行串行干擾消除后即可得到最終所需的數據，從而完成整個傳輸過程。

3.2 容量上界與可達速率域

在不考慮中繼轉發方式的情況下，可以推導出CoMABC方案的容量上界。對于采用DF中繼的可實現傳輸方案，可以得到其可達數據率域。

為了與已有方案進行比較，下面首先應用半雙工系統下的割集定理（cut-set theorem）[16]，推導出CoMABC方案的系統容量上界和可實現方案的可達數據率域。MABC以及TDBC方案的容量上界及可達數據率域在文獻 [12] 中有詳細推導。

多狀態網絡割集定理[17]給出了半雙工中繼系統的容量上界。為方便讀者，并給出后面的證明中將用到的重要定義，將對其進行簡要介紹。

割集定理[17]：對于有M個狀態N個節點的網絡，M和N均有限，割集C將節點分為2個集合S和SC（S的補集）。信息由發射節點集合S1發出，到達接收節點集合 S2， S1, S2? { 1,2,… ,N }，信息速率{Rij}是可達的，如果對網絡所處的任一狀態均滿足

其中，S滿足 S ∩ S1= S1, S ∩ S2=? ，非負時隙分配滿足；互信息量）表示在已知集合 SC的發射信號的情況下，從集合S中的發射節點到集合 SC中的接收節點所能傳輸的最大數據率。

下面用割集定理推導 CoMABC方案的容量上界。

命題 1 對于半雙工雙向中繼網絡，3時隙CoMABC方案的容量上界為Ra和Rb構成的凸集，Ra和Rb滿足條件：

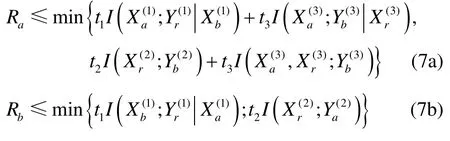
證明 根據多狀態網絡的割集定理，如圖2所示，網絡共有3個傳輸狀態，分別是t1時隙多址狀態，t2時隙廣播狀態和t3時隙協作發射狀態。

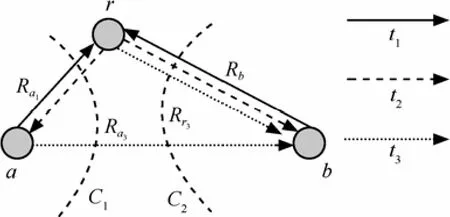
圖2 網絡割集

首先確定 b節點的發射數據率 Rb。發射集合S1= { b}，接收集合 S2= { a}。注意到 C2和 C1這 2個割(cut)分別對應于不同的、滿足條件S ∩ S1= S1, S ∩ S2=? 的 集 合S。 C2對 應 于S = { b}，而 C1對應于 S = { r,b}。根據割集定理，應在所有滿足條件的集合S上取最小，因此節點b的發射數據率如式（7b）所示。

可以采用同樣的方式確定節點a的數據率Ra，注意到節點a也在t3時隙發射。發射集合 S1= { a}，接收集合 S2= { b}，2個割 C1和 C2分別對應集合S = { a}以及 S = { a,r}。因此節點 a的數據率由式（7a）給出。

式（7）給出了用互信息量表示的CoMABC方案的容量上界。在本文考慮的信道模型下，此方案的容量上界還可以表示為

其中，C (x) = l b(1 + x )，x為接收信噪比。在AWGN信道下，信道系數h中只包含大尺度路徑損耗信息；而對于瑞利衰落信道，h包含大尺度和小尺度信息。

下面的命題給出了DF方式下可實現CoMABC方案的可達數據率域。

命題 2 半雙工雙向 DF中繼網絡，3時隙CoMABC方案的可達數據率域為Ra和Rb構成的凸集，Ra和Rb滿足條件：

證明 與命題一給出的上界相比，這里增加了式（9c）來約束t1時隙多址階段的數據率。下面根據方案的具體實現過程來證明數據率域是可達的。

Rb表示節點b的發射數據率，t1時隙節點b發射數據，中繼r接收并解碼；t2時隙中繼重新編碼后以適應r→a鏈路的調制方式把數據轉發至節點a，節點 a在刪去自干擾后即可得到所需的來自節點b的信息。因此Rb由式（9b）決定。

用Ra1表示節點a通過中繼轉發的數據率，包括與b節點對應的前2個時隙傳輸的數據，以及在 t3時隙由中繼單獨轉發的數據，因此 Ra1應該滿足

其中，Rr3表示第3個時隙中繼的最大傳輸數據率。

由于第1個時隙結束時，中繼需要對a、b 2路數據分別解碼，因此兩端數據率受多址信道容量的限制，故有約束：

在第3個時隙，中繼和節點a同時向節點b發射數據，節點b也需要將2路數據分別解出，因此t3時隙的和數據率也受多址容量的限制，有

其中，Ra3為t3時隙中節點a向節點b傳輸的新數據的數據率，與t1時隙的數據不同。Ra3和Rr3還應分別滿足

和

節點 a的發射數據率應為 Ra1和 Ra3之和，即Ra=Ra1+Ra3，帶入式（10）、式（12）和式（13），可得到式（9a）。

最后，由于Ra+Rb=Ra1+Ra3+Rb，由式（11）和式（13）即可得到式（9c）。

可實現CoMABC方案在AWGN以及瑞利衰落信道下的可達數據率域分別可以表示為

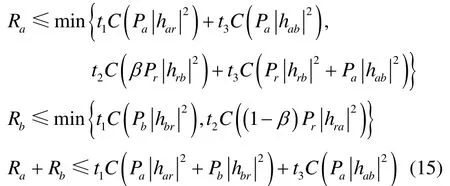
同樣，在AWGN信道下，信道系數h中只包含大尺度路徑損耗信息；而對于瑞利衰落信道，h包含大尺度和小尺度信息。

注意到在 DF模式下，在廣播階段需要進行功率分配，2路數據的發射功率分別為βP3和（1-β）P3，因此前2個不等式與上界中的表達有所不同。

3.3 資源分配優化問題

在得到 CoMABC方案的容量上界和可實現方案的可達數據率域后，可以對系統的加權和容量及加權和數據率進行優化。在蜂窩系統的應用場景下，如果節點a為基站，節點b為用戶，則Ra為系統的下行數據率，Rb為上行數據率。系統加權和數據率為uaRa+ubRb，可以反映出上下行數據率不對稱對系統性能的影響，這里，ua和ub為加權系數。當ua> ub時，Ra對加權和數據率影響較大；反之，ua< ub，Rb影響較大。當二者相等時即為和數據率。

從容量上界表達式（8）中可以看出，在節點位置信息確定后，CoMABC方案的容量上界與系統的時隙分配方案有關，因此通過對時隙分配進行優化，可以優化系統的加權和容量上界。

在單位傳輸時間的約束下，上述優化問題可以建模為

這是一個線性規劃問題，可以通過內點法[18]得到最優解。

同樣，從可達數據率域表達式（15）中可以知道，通過對功率和時隙分配進行聯合優化，可以得到前述可實現方案的最大可達加權和數據率。

這個優化問題可以建模如下：

這是一個更為復雜的非線性約束優化問題。不過，可以通過有效集的方法[18]解得。

4 仿真結果與分析

本節通過仿真對CoMABC、MABC以及TDBC這3種傳輸方案的系統加權和容量上界進行比較，也比較在DF方式下3種方案的加權可達和數據率。

MABC方案和TDBC方案的容量上界和可達數據率域由文獻[9]給出。容量上界與中繼處理方式無關，因此只需優化時隙分配，即可優化這2種方案的加權和容量上界，是線性規劃問題。對于DF模式下的加權可達和數據率，MABC和TDBC方案同樣需要中繼解碼，并進行功率分配后再廣播信號，因此也需要聯合優化時隙與功率分配因子。上述資源優化分配的方法與CoMABC方案相似。

圖3 簡化系統模型

為了便于分析與仿真，設中繼r位于基站a與用戶b的連線上，且與a的距離為d，如圖3所示，此時有當d在[0,1]之間變化時，中繼位置在a和b之間移動。仿真中3節點發射功率相等，即Pa= Pb= Pr= P，接收端的白高斯噪聲方差相等，均為σ2=1。在下面的仿真中，每個節點的發射功率均為Pσ2= 1 0 dB。

圖4比較了在AWGN信道下，當數據率加權系數 ua= ub= 1時，CoMABC方案與MABC和TDBC方案的系統和容量上界以及解碼轉發方式下的可達和數據率。

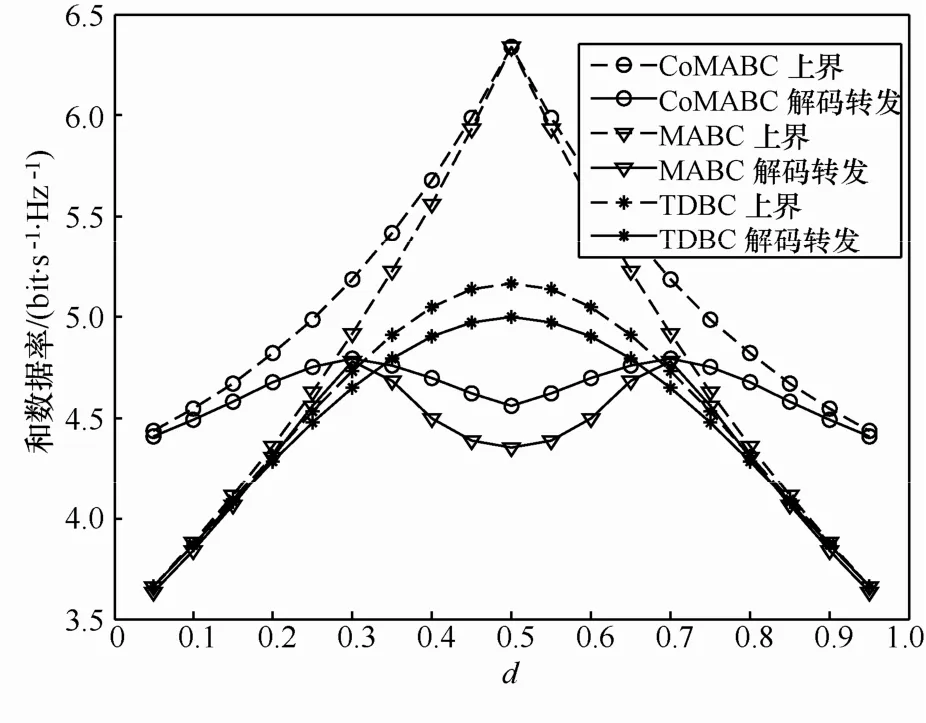
圖4 AWGN信道下各方案性能

可以看出，CoMABC方案的容量上界始終高于另外2種方案，同時CoMABC方案的可達和數據率始終高于 MABC方案。當中繼距離一端節點較近時，信道非對稱。如d<0.3時，距離節點a較近，而d>0.7時，距離節點b較近，此時，CoMABC方案始終優于MABC和TDBC方案，表明CoMABC方案更適于非對稱信道的場景。

表1給出了d=0.2和d=0.4（括號中數值）時3種方案在DF模式下的時隙與功率分配結果。

表1 d=0.2和d=0.4時，最優功率與時隙分配結果

數據表明，為了更好地分配雙向數據率，功率分配的優化結果都是向廣播階段較差的一條鏈路分配更多的功率。在非對稱信道下，我們的方案可以通過在第3個時隙進行協作發射來提高系統的和數據率。信道越不對稱，第3個時隙所分配的時間越長。

圖5給出了AWGN信道下d=0.2時3種傳輸方案的可達數據率域。

圖5 AWGN信道下DF模式下可達數據率域

可以看出，3種方案所支持的雙向數據率并不相同。TDBC方案的優化結果使得在廣播階段，中繼能夠恰好完全轉發前2個時隙接收到的a、b節點的發射數據，由于ra→鏈路性能較好，因此Rb較高。對于CoMABC方案，由于第3個時隙中繼和節點a同時向節點b傳輸，使得a節點發射的數據較多，Ra較大。MABC是二者的折中，兩端數據率分配得更加公平。但是從和數據率上來看，CoMABC更有優勢。

圖6給出了不同的加權因子對系統加權和容量和加權和數據率的影響。

圖6 AWGN信道下系統加權和容量及加權和數據率

圖6 (a)給出了ua=1、ub=2時3種方案的性能。可以看出，CoMABC方案幾乎始終優于另 2種方案，當中繼靠近基站b時，CoMABC方案優勢更加明顯。因此，當用戶在進行上行通信時，如果附近有中繼可以協作，則可以很好地提高系統的加權和數據率。

圖6(b)給出了ua=4、ub=1時，3種方案性能的比較，CoMABC方案也始終保持了最優的性能，且在節點b附近有明顯優勢。因此在實際系統中，基站在服務對下行數據率要求較高的用戶時，應該選擇距離基站較近的中繼進行協作傳輸。

圖7比較了瑞利信道下各方案的性能。

圖 7(a)給出了 ua= ub=1時 CoMABC方案與MABC和TDBC方案的和容量與和數據率，該仿真結果是對1 000次信道實現進行平均的結果，對每一次信道實現都進行了功率分配和時隙優化。可以看出在非對稱瑞利信道下，CoMABC方案性能依然優越，系統性能大大優于MABC和TDBC方案。

圖7 瑞利衰落信道下各方案性能

如果對每次信道實現都求解一次優化問題，系統實現復雜度很高。為此，考慮根據中繼位置、即根據大尺度信道信息，確定系統的功率分配因子和時隙分配，在小尺度信道衰落不同時下依然采用固定的分配方案，這樣只需在各節點位置確定時進行一次優化，從而大大降低復雜度。圖7(b)給出了固定時隙分配及功率分配因子時，在瑞利衰落信道下3種方案的性能。可以看出，即使時隙和功率分配并不是針對每次信道實現來優化的，在非對稱信道下，CoMABC方案依然能夠保持很好的性能，系統和數據率遠高于MABC和TDBC方案，且與二者相比，系統和數據率隨中繼位置變化很小。

當加權因子不同時，上述3種方案在瑞利衰落信道下的加權和數據率與 AWGN信道下的變化趨勢相同，這里不再贅述。

5 結束語

本文針對非對稱信道半雙工雙向中繼系統，提出了一種新的3時隙協作多址廣播傳輸方案，推導了所提出方案的容量上界以及在解碼轉發方式下的可達數據率域，并通過優化最優時隙分配以及功率分配參數，比較了系統在白高斯信道和瑞利衰落信道下的最大加權和容量與最大加權和數據率。分析和仿真結果表明，在非對稱雙向中繼系統中，所提出的CoMABC方案的性能優于已有方案。

[1] DOHLER M, LI Y H. Cooperative Communications: Hardware,Channel and PHY [M]. John Wiley & Sons, Ltd, 2010.

[2] LOUIE R, LI Y H, VUCETIC B. Practical physical layer network coding for two-way relay channels: performance analysis and comparison[J]. IEEE Trans Wireless Commun, 2010, 9(2):764 -777.

[3] WILSON M P, NARAYANAN K, PFISTER H D, et al. Joint physical layer coding and network coding for bidirectional relaying[J]. IEEE Trans Inf Theory, 2010, 56(11):5641-5654.

[4] ZHANG R, LIANG Y C, CHAI C C. Optimal beamforming for two-way multi-antenna relay channel with analogue network coding[J].IEEE J Sel Areas Commun, 2009, 27(5):699-712.

[5] CHEN M, YENER A. Multiuser two-way relaying: detection and interference management strategies[J]. IEEE Trans Wireless Commun,2009, 8(8):4296-4305.

[6] NGO H Q, QUEK T Q S, SHIN H. Amplify-and-forward two-way relay networks: error exponents and resource allocation[J]. IEEE Trans Commun, 2010, 58(9):2653-2666.

[7] ZHOU Q, LI Y, LAU F, et al. Decode-and-forward two-way relaying with network coding and opportunistic relay selection[J]. IEEE Trans Commun, 2010,58(9):1-7.

[8] CUI T, HO T, KLIEWER J. Memoryless relay strategies for two-way relay channels[J]. IEEE J Sel Areas Commun, 2009,57(10):3132-3143.

[9] KOIKE-AKINO T, POPOVSKI P, TAROKH V. Optimized constellations for two-way wireless relaying with physical network coding[J]. IEEE J Sel Areas Commun, 2009, 27(5):773-787.

[10] RANKOV B, WITTNEBEN A. Spectral efficient protocols for half-duplex fading relay channels[J]. IEEE J Sel Areas Commun, 2007,25(2):379-389.

[11] LARSSON P, JOHANSSON N, SUNELL K E. Coded bi-directional relaying[A]. Proc IEEE Vehicular Technology Conf[C]. 2006. 851-855.

[12] KIM S J, MITRAN P, TAROKH V. Performance bounds for bi-directional coded cooperation protocols[J]. IEEE Trans Inf Theory,2008, 54(22):5235-5241.

[13] ZHAO J, KUHN M, WITTNEBEN A, et al. Asymmetric data rate transmission in two-way relaying systems with network coding[A].Proc IEEE Int Conf Communications (ICC’10)[C]. 2010. 1-6.

[14] PAN C, ZHENG J. Mapping codebook-based physical network coding for asymmetric two-way relay channels[A]. Proc IEEE Int Conf Communications (ICC’10)[C]. 2010.1-5.

[15] PARK J M, KIM S L, CHOI J. Hierarchically modulated network coding for asymmetric two-way relay systems[J]. IEEE Trans Vehicular Technology, 2010, 59(5):2179-2184.

[16] FITZEK H, KATZ D. Cooperation in Wireless Network Principles and Application[M]. Springer, 2006.

[17] KHOJASTEPOUR M. Distributed Cooperative Communications in Wireless Networks[D]. Dept of Electrical and Computer Engineering,Rice University, 2004.

[18] 陳寶林.最優化理論與算法[M]. 北京: 清華大學出版社, 2005.CHEN B L. Optimal Theories and Methods[M]. Beijing: Tsinghua University Press, 2005.