一種適合于旋翼前飛非定常流場計算的新型運動嵌套網格方法

王 博，招啟軍，徐 廣，徐國華

（南京航空航天大學 直升機旋翼動力學重點實驗室，江蘇 南京210016）

0 引 言

旋翼是直升機最主要的氣動部件，其氣動特性不僅對直升機的飛行性能起著舉足輕重的作用，還對振動、噪聲等特性產生重要影響。因此，旋翼的空氣動力學特性是直升機研究領域的重要研究內容之一，是研發具有我國自主知識產權直升機旋翼設計的前提和基礎。目前，關于旋翼氣動特性的研究方法主要分為兩類：試驗方法和數值模擬方法。采用試驗方法可以較準確地獲得旋翼氣動特性，但是存在成本高、周期長等缺點。而數值模擬方法可以有效避免這些缺點，因此，開展旋翼氣動特性數值模擬研究具有重要現實意義。

目前常見的旋翼氣動特性計算方法主要分為渦方法［1－2］和計算流體力學（CFD）方法［3－6］。渦方法是一種相對成熟的方法，在傳統槳葉氣動特性的模擬、預測方面具有良好的效果，且具有很高的計算效率。然而，伴隨著直升機技術的發展，旋翼的氣動外形設計要求不斷提高，渦方法由于其基于勢流假設，很難精確模擬現代直升機旋翼的氣動特性和流場，尤其是槳尖附近的細節流場特征。而基于Euler／N－S方程的CFD方法可以滿足新型槳葉流場模擬的精度需要，因而成為了新的研究熱點。然而，相對于固定翼飛機的CFD模擬，旋翼CFD方法含有很多技術難點，其中關鍵的一點是網格方案。旋翼除旋轉運動外，還同時存在獨特的揮舞、變距等運動，這些運動將對其自身的空氣動力學和動力學特性產生重要影響，并直接導致旋翼貼體網格生成的困難，因此目前通常采用嵌套網格方法。但由于隨著方位角的不斷變化，槳葉與背景網格之間的相對位置也在改變，所以在采用嵌套網格方法計算時必須不斷地刷新網格間的嵌套關系，這對嵌套網格方法的效率和魯棒性提出了嚴峻的挑戰。

使用嵌套網格時需要在網格重疊部分進行插值，因此必須判斷網格間的單元對應關系，而判斷方法的效率和魯棒性將直接影響嵌套網格技術的實用性。為解決這一關鍵技術，國內外學者提出了很多搜索判斷方法［7－12］。傳統的表面向量法［7］需要預設洞邊界，并且在判斷每個給定點時都需要尋找與該點最近的交接面的面單元，因而效率不高。射線法［8］對給定點做射線，根據射線與邊界交點的數量判斷是否在洞內，同樣由于需要在判斷每一個點時循環計算交接面上的面單元導致計算效率很難提高。洞映射方法［9］建立與原網格對應的輔助均勻笛卡爾網格，用輔助網格近似原網格的挖洞曲面，該方法效率和自動化程度都很高，但是當參考網格較密時會消耗較多的內存。而基于洞映射方法和射線法的目標射線法通過建立垂直于某一方向的輔助網格，判斷點在沿該方向的射線與邊界交點的數量判斷點的屬性，同時具有效率高和內存消耗小的優點，但由于混合了洞映射方法和目標射線法算法復雜度有所增加。國內的學者也有提出多種洞單元識別方法［10－12］，獲得了一定的效果。

通過吸收洞映射法思想，結合旋翼流場計算網格特點，本文提出了一種新的“透視圖”挖洞方法用以解決前飛旋翼流場計算中笛卡爾背景網格和結構網格之間的嵌套關系，與前面提到的多種方法相比較，該方法同時具備節省內存、算法簡單、高效、可靠等特點，適合于旋翼懸停／前飛狀態的計算。Inverse Map［13］是嵌套網格技術中又一重要技術方法，用于尋找覆蓋于給定點在曲線網格上貢獻單元，本質也是判斷網格間的單元對應關系，因此將此方法推廣到Inverse Map的建立過程中，相對于傳統建立方法有效地提升了效率。最后，本文采用提出的嵌套網格方法對旋翼懸停／前飛流場進行了計算，驗證了該方法的有效性。

1 嵌套網格方法

1.1 “透視圖”挖洞方法

該方法的基本思路是：遍歷槳葉網格（細網格）中物面點并計算其在粗網格（背景網格）上的對應單元序號，將這些序號保存在相應的數組里，最后由這一數組即可在粗網格上重現對應的槳葉形狀，所得到的形狀即為洞的最小邊界，并可用來標記洞單元。用同樣的方法可以通過遍歷槳葉網格外圍的點獲得洞的最大邊界。

“透視圖”方法主要分為以下四步驟：

第一步，建立槳葉網格以背景網格尺寸為分辨率的數組，并獲取相關的網格參數；

第二步，循環網格中壁面點，根據點在背景網格的單元的序號更新已經建立的數組，最后獲得物面的“透視圖”，該圖標明了挖洞的最小范圍；

第三步，循環網格外表面點，根據點在背景網格的單元的序號更新已經建立的數組，最后獲得物面的“透視圖”，該圖標明了挖洞的最大范圍；

第四步，根據所建立的“透視圖”進行洞點的判斷。

以二維網格為例，如圖1所示，在尺寸為N×M的笛卡爾背景網格上對一翼型網格挖洞，“透視圖”方法的基本算法如下：

（1）建立尺寸為N×4的整數數組T，其中N為背景網格的I方向單元數，數組初始化為0。

（2）循環網格的物面點，根據P點坐標計算其所在背景單元的序號i，j。依次作如下運算：

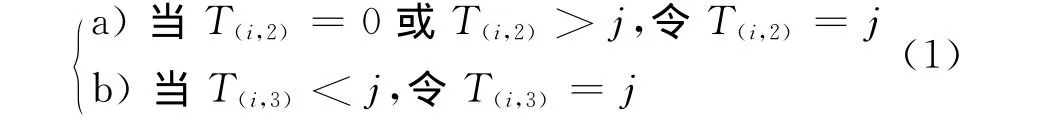
（3）循環網格的外表面點，根據P點坐標計算其所在背景單元的序號i，j（因與物面點循環過程類似，圖1并未給出）。依次作如下運算：

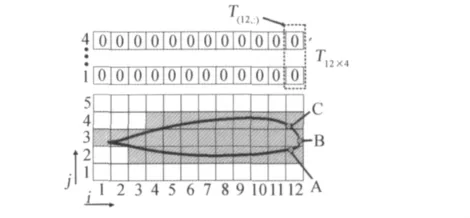
圖1 二維翼型“透視圖”法挖洞示意圖Fig.1 Schematic of the top view map method for hole－cutting around 2Dairfoil

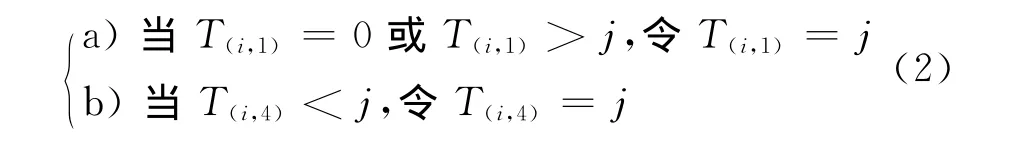
圖2給出了循環物面點時，數組T中某一列的變化過程。當最終循環完所有物面點，數組T如圖3所示。其中數字與圖1中陰影部分相吻合。

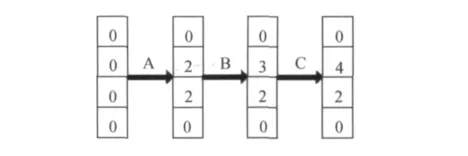
圖2 循環計算 A、B、C點時T（12，：）變化過程Fig.2 Change process of T（12，：）when cycling A，B，and C points

（4）標記洞單元，如圖4所示，根據需要可改變算法來選擇洞的大小：

a）根據T（i，1）、T（i，4）的值對第i列背景網格單元V（i，j）做標記，可得到最大范圍的洞。判斷條件如下：

b）根據T（i，2）、T（i，3）的值對第i列背景網格單元C（i，j）做標記，可得到最小范圍的洞。判斷條件如下：

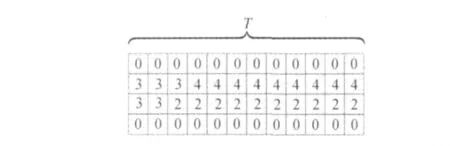
圖3 完成物面點循環后的數組TFig.3 Array Tafter completing cycling points on the wall surface

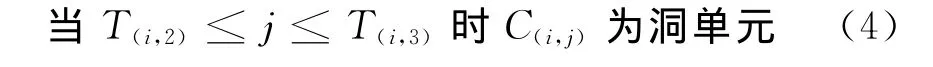
如圖4（a）所示，按照最大范圍策略對網格標記洞單元得到的最大范圍的洞與網格外邊界緊密貼合，這種挖洞策略適用于流場非線性程度較高的場合，例如前飛時槳葉尖部出現激波的位置。圖4（b）中顯示了采用最小范圍內挖洞策略，洞邊界恰好嚴密地包圍了槳葉表面網格，這種方法適合于對洞大小限制較強的情況，例如槳葉片數較多時，槳葉根部間距較小的狀態。

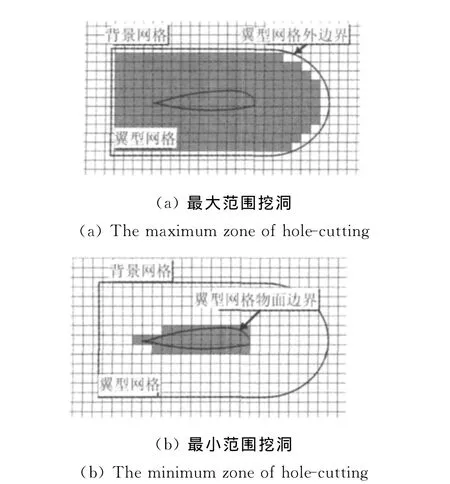
圖4 不同挖洞策略Fig.4 Different strategies of hole－cutting

值得注意的是在生成“透視圖”數組時可以選擇一次性生成包含所有槳葉的數組，也可以分別生成每片槳葉的數組。采用后一種方法生成的不同“透視圖”之間可以發生重疊，因此該方法可拓展用于帶機身的旋翼／機身干擾流場計算中。

1.2 挖洞測試

為驗證“透視圖”法的執行效率和魯棒性，設計了一組測試算例。

（1）在頻率為2.6GHz的 Dual－Core PC上，對兩片槳葉進行動態挖洞，背景網格尺寸為120×62×120均勻笛卡爾網格，槳葉網格尺寸為159×13×83，槳葉表面點共有10587個點，方位角由0°到90°，每3°挖洞一次。消耗時間如圖5所示，從圖中可以看出，當槳葉在不同方位角時挖洞消耗的時間基本相同。

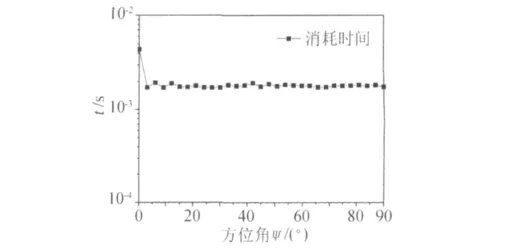
圖5 不同方位角挖洞所消耗時間Fig.5 Consuming time of hole－cutting at different azimuthal angles

（2）由于采用N－S方程進行計算時，需要物體表面網格尺寸滿足一定的尺寸需求，這會導致網格數量大幅增加。為測試該挖洞方法的速度隨槳葉網格尺寸增加的變化，分別生成了槳葉表面點數為1×10587～8×10587的槳葉網格。不同槳葉網格挖洞消耗時間如圖6所示。可以看出，消耗時間隨著槳葉表面網格點的變化基本上為線性增長。這是因為在建立“透視圖”數組時所循環的點只針對槳葉網格的物面點和表面點。如對I×J的二維網格，需要計算的點的數量小于I×2，三維情況下小于I×J×2。

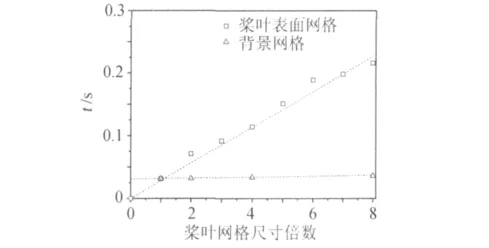
圖6 挖洞時間與槳葉網格尺寸關系Fig.6 Relationship between hole－cutting time and blade mesh size

（3）為測試該挖洞方法的速度隨背景網格尺寸增加的變化，分別生成了尺寸為120×124×120（2倍）、240×62×240（4倍）和240×124×240（8倍）的均勻背景網格。采用與前面相同的測試方法，在不同背景網格挖洞消耗時間如圖6所示。從圖中可以看出，背景網格尺寸增加對計算時間的影響明顯弱于槳葉網格尺寸。這主要是因為對于均勻背景網格，查找背景網格單元序號的計算量并沒有太大變化，而標記洞單元消耗時間占總消耗時間比重較少。對于非均勻直角網格，由于采用了二分法查找單元序號，計算量增加很小。

（4）在前飛狀態下，由于槳葉同時存在揮舞運動、變距運動和擺振運動，運動規律較為復雜，這就需要網格方法具有較強的魯棒性。作為方法驗證，選取β＝×cos（ψ）為揮舞運動規律，θ＝×cos（ψ＋）為周期變距，ψ為方位角，應用所建立的方法進行挖洞，并對洞邊界進行檢測驗證所建立的方法的可靠性。測試結果表明在所有給出狀態下都可以正確的進行洞點識別。從圖7中可以看出不同方位角時挖洞時間基本相同。

圖7 計入揮舞及變距運動情況下挖洞消耗時間Fig.7 Consuming time of hole－cutting when considering flapping and pitching motions

1.3 隱含條件的處理及其意義

在使用“透視圖”方法挖洞時存在一個隱含的條件，即在需要挖洞的區域內槳葉網格的密度必須大于背景網格。在實際應用中，為在保證計算精度需要的基礎上減少計算時間，背景網格的網格點密度往往小于旋翼槳葉的密度。但作為可靠性考慮，對這種情況進行簡單的討論。如圖8所示，當不能滿足這一條件將有可能導致“遺漏”洞單元的情況有兩種。第一種，由于翼型上表面和下表面在第9列上都沒有網格點，最終會導致在第9列上遺漏了3個洞單元。而在第7列，由于下表面沒有相應的網格點導致少識別2個洞單元。

當出現這種遺漏洞單元的情況，可以采用兩種解決辦法：

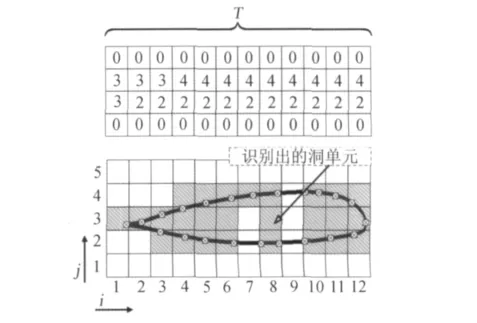
圖8 挖洞可能出現的“遺漏”現象Fig.8 The possible missing phenomenon during the process of hole－cutting

（1）可以對物面網格點進行插值細分，保證物面網格點相鄰兩點間的最大距離小于背景網格上相鄰兩點間的最小間距即可。

（2）建立網格點密度較低的參考背景網格，在保證隱含的條件的基礎上對參考背景網格挖洞，然后按照參考背景網格的洞單元對背景網格單元進行標記。

由2.2節的測試結果可以看出，采用第一種方法會導致計算時間的線性增長，但是在實際編程過程中這一方法實現較為簡單，在原始挖洞時間較小的情況下可以采用這一方法。采用第二種方法增加了數據結構的復雜度，但是可以保證消耗時間增長不大，適合于對挖洞時間有較高要求的情況。

從另一方面來看，由于只要滿足隱含條件即可保證挖洞的需要，那么就可以通過適當減少物面點的判斷來減少計算量，進一步減少挖洞過程消耗的時間。如圖1中所示，實際上只需要循環A、C兩點即可得到正確的T（12，：）。

1.4 非結構網格上的使用

前述方法只適合于背景網格為結構網格的情況，當背景網格為非結構網格時，由于網格單元間為無序排列，因此不能直接使用該方法進行挖洞。

為解決網格單元無序排列的問題，可以在對應的空間范圍內建立結構化的參考網格，在計算前生成背景網格單元與參考網格單元之間的映射關系。通過參考網格映射可以將前述方法應用于非結構背景網格的挖洞過程。

1.5 透視圖法在Inverse Map建立中的應用

嵌套網格方法中另一關鍵技術就是對貢獻單元的搜尋，目前的搜尋方法基本都采用Inverse Map（IM）法［13］。在搜索某一點的貢獻單元時，采用該方法可以將待搜索的貢獻單元數量減少到幾個甚至一個。目前在旋翼前飛流場 計算中主要采用剛性槳葉假設，只需要生成一次IM就可以滿足使用的需要。但是當采用彈性假設時，槳葉網格會發生變形，必須重新生成。在這種情況下，由于需要多次生成IM，因此IM的生成效率變得非常重要。

將“透視圖”法應用于IM的生成需要改變的地方有兩點。

（1）數組T尺寸變為NI×MI×4，其中NI、MI為IM的尺寸。

（2）遍歷槳葉上所有的網格點。保存在數組 中的參數由背景網格序號改為槳葉網格點在槳葉網格上的序號，所采用判斷法則相同。

在建立好的數組中，T（i，j，1）為IM 上（i，j）單元在槳葉網格上對應的I方向序號的下限。T（i，j，2）為I方 向 序 號 的 上 限。T（i，j，3）為J方 向 序 號 的 下 限。T（i，j，4）為J方向序 號 的 上 限。 即T（i，j）對 應 的 貢 獻 單元為B（ib，jb），其中T（i，j，1）≤ib≤T（i，j，2）、T（i，j，3）≤jb≤T（i，j，4）。

在計算量方面：首先，由于生成IM時需要循環槳葉網格上所有的單元，因此遍歷并計算的點的數量大于挖洞所處理的點。其次，一般情況下IM為均勻網格，因此查找某一點在其上對應的單元序號可直接通過除法計算得到，因此總體計算量無明顯變化。

2 流場求解方法

2.1 控制方程

對前飛流場數值模擬，采用以絕對物理量為參數的守恒的積分形式的NS方程為主控方程：

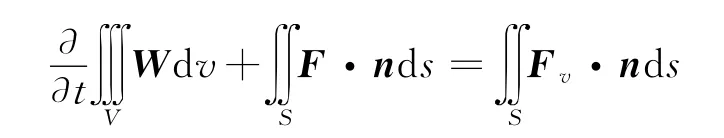
其中：

在以上各式中，q＝（u，v，w）T表示絕對速度，qr表示網格運動速度，E和H分別為總能和總焓，粘性相關項為Txx＝2μux－（2／3）μ▽q，Txy＝μ（uy＋ux），φx＝uTxx＋vTxy＋wTxz＋k?T／?x等。其中，V為控制體單元，S為單元面積，n表示單元表面法矢量，t為物理時間，μ、k、T分別為粘性系數、熱傳導系數和絕對溫度。湍流模型采用B－L模型。

2.2 方程離散

本文時間推進采用顯式五步Runge－Kutta迭代格式。空間離散采用格心形式的Jameson中心平均有限體積法，相鄰單元交接面處的數值通量采用平均計算。另加入由二、四階混合導數組成的人工粘性項消除中心差分具有奇偶失關聯及高頻誤差的等缺點，避免了由無阻尼引發的非線性（如激波）數值振蕩。為加快收斂速度還另外采用了隱式殘值光順等技術。

2.3 計算網格

計算網格采用嵌套網格技術。直接采用上述“透視圖”法來確定洞點以及洞邊界，并用“透視圖”法加速Inverse Map生成。以7A旋翼［14］為例，網格由兩部分組成，槳葉網格采用C－O型網格，尺寸為159×30×83，背景網格采用笛卡爾網格，尺寸為166×140×166，背景網格上邊界距離槳盤平面為3R，下邊界距離槳盤平面為5R，周向邊界距離槳轂中心軸為10R。為了比較準確地捕捉槳尖渦，以及減少數值耗散，在背景網格中槳葉運動附近區域進行了加密，該處的網格尺寸為0.1倍弦長。在背景網格上，采用Euler方程求解槳葉的流場和捕捉遠場尾跡。

2.4 邊界條件

槳葉表面的熱力學和動力學邊界條件分別取作法向導數為零，即＝0和＝0，在遠場取基于Ri－emann不變量的遠場邊界條件。對于旋翼網格及背景網格之間的流場信息交換由三線性插值來完成。

3 旋翼前飛流場計算及結果分析

3.1 UH－60A旋翼

為驗證本方法在新型槳尖上使用的可靠性，選取UH－60A旋翼算例，由于公開發表的文獻中給出的試驗狀態數據不全，因此選擇懸停狀態試驗［15］結果進行對比。該模型旋翼有4片槳葉，展弦比15.3。該旋翼的槳葉外形較7A旋翼更為復雜，槳葉尖部具有20°后掠；槳葉分為三段，由兩種不同的翼型組成；負扭轉分布為非線性負扭轉，最大扭轉為13°。計算狀態為：Mtip＝0.628，θ0.75＝9°。

圖9給出了0.775R和0.92R處的槳葉表面壓強系數分布。從圖中可以看出，旋翼靠近中間的部分和靠近外側的計算結果與試驗值吻合良好。圖10給出了懸停效率的計算值與試驗值的比較，可以看到計算結果的趨勢和試驗值一致。這表明所建立的挖洞方法結合基于N－S方程的求解器，能有效地模擬新型槳尖旋翼流場。

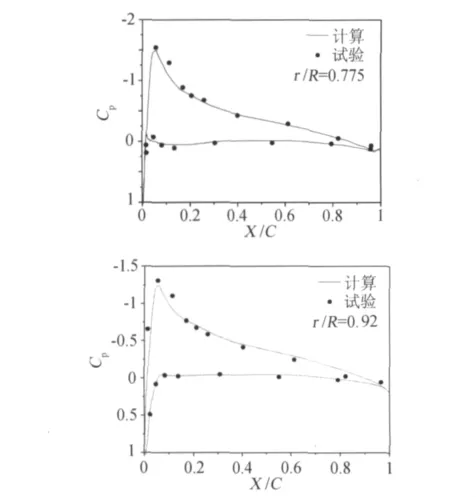
圖9 UH－60A旋翼槳葉表面壓強系數分布Fig.9 Distributions of pressure coefficient on the blade surface of the UH－60Arotor

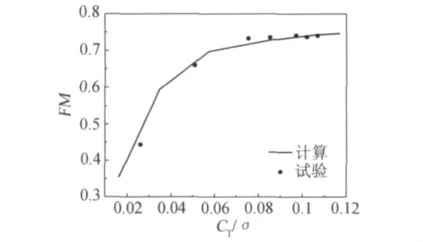
圖10 UH－60A旋翼懸停效率隨拉力系數的變化Fig.10 Predictions of Figure of Merit versus CT／σfor the UH－60Arotor，compared with experimental data

3.2 HELISHAPE 7A旋翼

為了驗證本文給出的"頂透視圖"挖洞方法的高效和可靠性，計算了前飛狀態旋翼的氣動特性。選用有試驗結果可以對照的HELISHAPE 7A旋翼［14］作為算例。該旋翼有4片槳葉，直徑4.2m，展弦比15，實度σ≈0.0849，槳葉平面形狀為矩形。HELISHAPE 7A旋翼的槳葉氣動外形較復雜，槳葉分為三段，每段由不同的翼型組成，且有非常規的幾何負扭轉（－3.95°）。計算狀態為：Mtip＝0.616，μ＝0.167。

為驗證所建立方法的的有效性，分別對比了“透視圖”法和從全局遍歷方法查找對應點方法所消耗的時間。從表1中可以看出，采用“透視圖”法后，無論是洞點單元標記還是Inverse Map生成速度都有了很大的提高。速度的提高主要因為計算時只需要循環計算槳葉網格點邊界點在背景網格上的坐標一遍即可，避免了全局查找方法中的大量查找過程。其次，計算量中主要部分在于查找點P在的背景網格單元序號，這在本質上來說是一個有序數組的查找問題，可用成熟的查找算法加速。

表1 使用與不使用“透視圖”方法所用時間的比較Table 1 Comparisons of consuming time between using and not using top－view map method

圖11給出了三個不同方位角上槳葉槳葉表面壓強系數與試驗值結果［14］的對比。如圖所示ψ＝90°時在槳葉尖部，結合該挖洞方法的N－S方程計算得到的槳葉上下表面壓強系數與試驗值較為接近；ψ＝180°時槳葉表面壓強系數的分布，結果優于90°時計算結果。圖11（c）給出方位角為270°時槳葉表面壓強系數的分布。計算結果表明采用“透視圖”法的流場求解器可以在保證計算結果正確性的前提下有效地提高旋翼前飛非定常流場的計算效率。

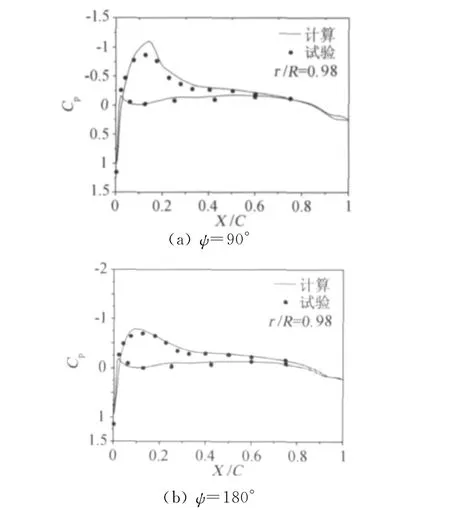
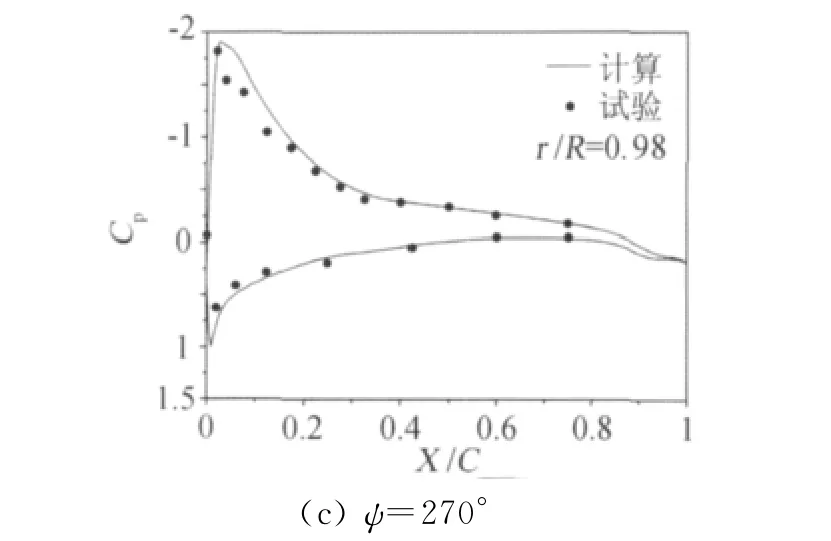
圖11 7A旋翼前飛狀態槳葉表面壓強系數分布Fig.11 Surface pressure coefficient of the 7Arotor in forward flight

4 結 論

結合旋翼流場實際計算情況，提出了一種快速確定嵌套網格中不同網格單元之間對應關系的方法，通過多種算例驗證，得到如下結論：

（1）“透視圖”挖洞方法采用簡單的計算方法進行網格關系判斷，可快速完成網格間嵌套關系的建立，滿足旋翼懸停／前飛流場計算時所需要的動態挖洞要求。隨著網格尺寸的增加，計算量增加較小，同時該算法具有節省內存、魯棒性強的特點，具有重要工程實用價值。

（2）基于新的挖洞技術，建立了一個嵌套網格CFD方法，較為成功地應用于直升機懸停／前飛狀態旋翼流場的計算，為進一步開展先進氣動外形旋翼數值模擬研究打下了良好的基礎。

（3）將“透視圖”方法應用于Inverse Map的生成可以大幅度減少建立Inverse Map所需的時間。

［1］BAGAI A，LEISHMAN J G.Rotor free－wake modeling using apseudo implicit relaxation algorithm［J］.Journal ofAircraft，1995，32（6）：1276－1285.

［2］李春華，徐國華.懸停和前飛狀態傾轉旋翼機的旋翼自由尾跡計算方法［J］.空氣動力學學報，2005，23（2）：152－156.

［3］KANG H J，KWON O J.Unstructured mesh Navier－Stokes calculations of the flow field of a helicopter rotor in hover［J］.JournaloftheAmericanHelicopterSociety，2002，47：90－99.

［4］解福田，宋文萍，韓忠華.低耗散格式在旋翼前飛氣動噪聲預測中的應用研究［J］.西北工業大學學報，2009（2）：151－156.

［5］牟斌，肖中云，周鑄，等.直升機旋翼懸停流場的粘性數值模擬［J］.空氣動力學學報，2009，27（5）：582－585.

［6］葉靚，招啟軍，徐國華.基于非結構嵌套網格和逆風格式的旋翼懸停流場數值模擬［J］.空氣動力學學報，2009，27（1）：62－66.

［7］SLOTNICK J P，KANDULA M，BUNING P G.Navier－Stokes simulation of the Space Shuttle launch vehicle flight transonic flowfield using a large scale chimera grid system［A］.12th AIAA Applied Aerodynamics Conference［C］.Colorado Springs，Colorado，USA，1994.

［8］MEAKIN R L.Object X－rays for cutting holes in composite overset structured grids［A］.15th AIAA Computational Fluid Dynamics Conference［C］.Anaheim，California，USA，2001.

［9］ROGERS S E，DIETZ W E，SUHS N E.PEGASUS 5：an automated preprocessor for overset－grid computational fluid dynamics［J］.AIAAJournal，2003，41（6）：1037－1045.

［10］李亭鶴，閻超.一種新的分區重疊洞點搜索方法－感染免疫法［J］.空氣動力學學報，2001，19（2）：156－160.

［11］李亭鶴，閻超，李躍軍.重疊網格技術中割補法的研究與改進［J］.北京航空航天大學學報，2005，31（4）：402－406.

［12］楊文青，宋筆鋒，宋文萍.高效確定重疊網格對應關系的距離減縮法及其應用［J］.航空學報，2009，30（2）：205－212.

［13］MEAKIN R.A new method for establishing intergrid communication among systems of overset grids［A］.10th AIAA Computational Fluid Dynamics Conference［C］.Honolulu，Hawaii，USA，1991.

［14］POMIN H，WAGNER S.Navier－Stokes analysis of helicopter rotor aerodynamics in hover and forward flight：Rotor wakes［J］.JournalofAircraft，2002，39（5）：813－821.

［15］LORBER P，STAUTER R，LANDGREBE A.A comprehensive hover test of the airloads and airflow of an extensively instrumented model helicopter rotor［A］.45th AHS Annual Forum［C］.Boston，Massachusetts，USA，1989.